A New Attribute Decision Making Model Based on Attribute Importance ()
1. Introduction
Decision making is choosing a strategy among many different projects in order to achieve some purposes. According to various decision criteria, the decision-making problem is formulated as three different models: high risk decision, usual risk decision and low risk decision. With different attitude of decision makers for different types of decision models, decision criteria are formulated as five different models: optimistic-decision criterion, pessimistic-decision criterion, evenness-decision criterion, minimum-risk-decision criterion, compromise-decision criterion.
Rough set theory [1,2], a new mathematical approach to deal with inexact, uncertain or vague knowledge, has recently received wide attention on the research areas in both of the real-life applications and the theory itself. And the real-life applications speed up the theory research about rough set. Rough set theory is an extension of set theory, in which a subset of a universe is described by a pair of ordinary sets called the lower and upper approximations. Rough set theory is emerging as a powerful theory dealing with imperfect data. It is an expanding research area which stimulates explorations on both realworld applications and on the theory itself. It has found practical applications in many areas such as knowledge discovery, machine learning, data analysis, approximate classification, conflict analysis, and so on. The theory of rough sets has been successfully applied to diverse areas, such as pattern recognition, artificial intelligent, machine learning, knowledge acquisition, economy forecast, data mining and so on [3,4]. Rough set theory adopts the concept of equivalence classes to partition the training instances according to some criteria. Two kinds of partitions are formed in the mining process: lower approximations and upper approximations, from which certain and possible rules are easily derived. It operates only on the data and does not require any added information; it is completely data-driven.
But there are still some defects in the Pawlak rough set. Classification must be correct absolutely in Pawlak rough set model, so classical model cannot deal with datasets effectively which have noisy data. Some latent useful knowledge may be abandoned. Researchers have put forward many extended rough set models combining with other soft computing theories, such as dominance-based rough set [5], rough fuzzy set [6] and fuzzy rough set [7] and so on. Probabilistic rough set [8], variable precision rough set [9] and bayesian rough set [10] are one of the most important branches. Variable precision rough set model was aimed at handling uncertain and noisy information and was directly derived from the original roughset model without any additional assumptions [9]. It integrated the concept of rough inclusion relation into the Pawlak rough set model, thus being able to allow for some degree of misclassification in the mining process. Probabilistic rough set approximations can be formulated based on the notions of rough membership functions [11] and rough inclusion [12]. Also, rough set over dual-universe is studied [13].
Since extended models introduction, they have been used in many research fields successfully. In these models, decisions about new problems are made according rules extracted. However, some attributes of new problems are inconsistent with rules completely. In this situation, how to make decision might well repay investigation.
In this paper, considering imperfectly matching between new problem and rules exit, we introduce relative importance when deal with new problems. Firstly, we present same basic concept of rough set. Then we construct a new multiple attribute decision making model by considering relative importance of attribute. Finally, an example is advanced to illustrate our model.
2. Preliminaries
The rough set theory, firstly introduced by Pawlak in 1982, is a valuable mathematical tool for dealing with vagueness and uncertainty [10,11]. A rough set is a formal approximation of a crisp set (i.e., conventional set) in terms of a pair of sets which give the lower and the upper approximation of the original set.
Let  be an information system (attributevalue system), where U is a non-empty set of finite objects (the universe) and A is a non-empty, finite set of attributes such that
be an information system (attributevalue system), where U is a non-empty set of finite objects (the universe) and A is a non-empty, finite set of attributes such that 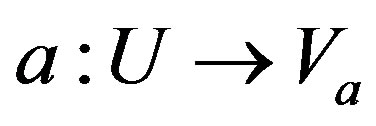 for every
for every .
. 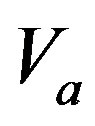 is the set of values that attribute a may take. The information table assigns a value
is the set of values that attribute a may take. The information table assigns a value 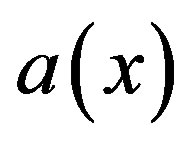 from
from  to each attribute a and object x in the universe U. With any
to each attribute a and object x in the universe U. With any 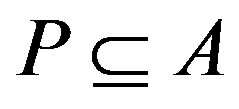 there is an associated equivalence relation IND(P):
there is an associated equivalence relation IND(P):
 (1)
(1)
The relation IND(P) is called a P-indiscernibility relation. The partition of U is a family of all equivalence classes of IND(P) and is denoted by  (or
(or ). If
). If , then x and y are indiscernible (or indistinguishable) by attributes from P.
, then x and y are indiscernible (or indistinguishable) by attributes from P.
Let  be a target set that we wish to represent using attribute subset P; that is, we are told that an arbitrary set of objects X comprises a single class, and we wish to express this class (i.e., this subset) using the equivalence classes induced by attribute P.
be a target set that we wish to represent using attribute subset P; that is, we are told that an arbitrary set of objects X comprises a single class, and we wish to express this class (i.e., this subset) using the equivalence classes induced by attribute P.
However, the target set X can be approximated using only the information contained within P by constructing the P-lower and P-upper approximations of X:
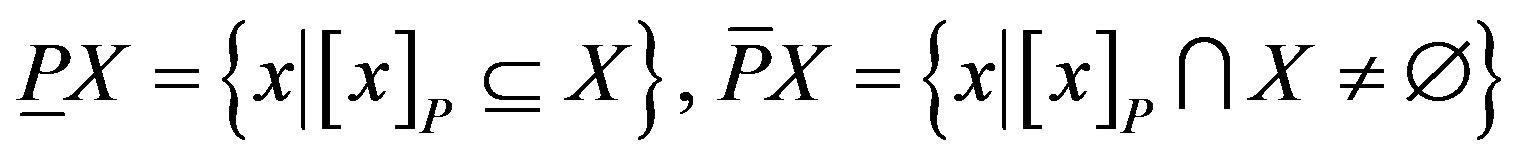 (2)
(2)
The P-lower approximation, or positive region, is the union of all equivalence classes in 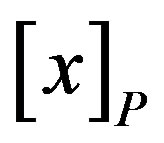 which are contained by (i.e., are subsets of) the target set. The lower approximation is the complete set of objects in
which are contained by (i.e., are subsets of) the target set. The lower approximation is the complete set of objects in 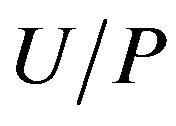 that can be positively (i.e., unambiguously) classified as belonging to target set X.
that can be positively (i.e., unambiguously) classified as belonging to target set X.
The P-upper approximation is the union of all equivalence classes in 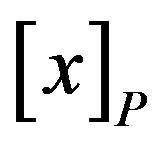 which have non-empty intersection with the target set. The upper approximation is the complete set of objects that in
which have non-empty intersection with the target set. The upper approximation is the complete set of objects that in  that cannot be positively (i.e., unambiguously) classified as belonging to the complement (
that cannot be positively (i.e., unambiguously) classified as belonging to the complement (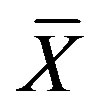 ) of the target set X. In other words, the upper approximation is the complete set of objects that are p.
) of the target set X. In other words, the upper approximation is the complete set of objects that are p.
In summary, the lower approximation of a target set is a conservative approximation consisting of only those objects which can positively be identified as members of the set. (These objects have no indiscernible “clones” which are excluded by the target set.) The upper approximation is a liberal approximation which includes all objects that might be members of target set. (Some objects in the upper approximation may not be members of the target set.) From the perspective of , the lower approximation contains objects that are members of the target set with certainty (probability = 1), while the upper approximation contains objects that are members of the target set with non-zero probability (probability > 0).
, the lower approximation contains objects that are members of the target set with certainty (probability = 1), while the upper approximation contains objects that are members of the target set with non-zero probability (probability > 0).
An interesting question is whether there are attributes in the information system (attribute-value table) which are more important to the knowledge represented in the equivalence class structure than other attributes. Often, we wonder whether there is a subset of attributes which can, by itself, fully characterize the knowledge in the database; such an attribute set is called a reduct.
Formally, a reduct is a subset of attributes  such that 1)
such that 1)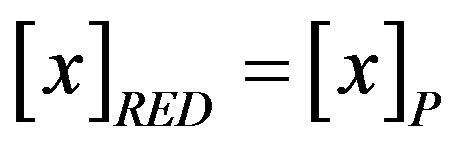 , that is, the equivalence classes induced by the reduced attribute set RED are the same as the equivalence class structure induced by the full attribute set P.
, that is, the equivalence classes induced by the reduced attribute set RED are the same as the equivalence class structure induced by the full attribute set P.
2) the attribute set RED is minimal, in the sense that 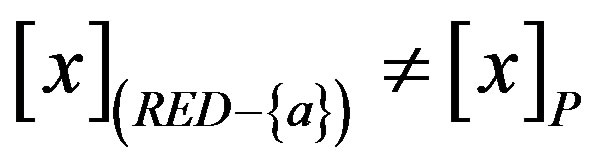 for any attribute
for any attribute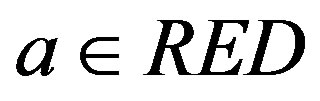 ; in other words, no attribute can be removed from set RED without changing the equivalence classes
; in other words, no attribute can be removed from set RED without changing the equivalence classes .
.
A reduct can be thought of as a sufficient set of features—sufficient, that is, to represent the category structure.
One of the most important aspects of database analysis or data acquisition is the discovery of attribute dependencies; that is, we wish to discover which variables are strongly related to which other variables. Generally, it is these strong relationships that will warrant further investigation, and that will ultimately be of use in predictive modeling.
In rough set theory, the notion of dependency is defined very simply. Let us take two (disjoint) sets of attributes, set P and set Q, and inquire what degree of dependency obtains between them. Each attribute set induces an (indiscernibility) equivalence class structurethe equivalence classes induced by P given by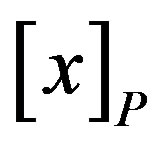 , and the equivalence classes induced by Q given by
, and the equivalence classes induced by Q given by .
.
Let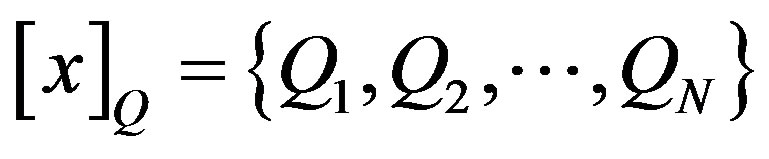 , where
, where 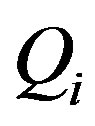 is a given equivalence class from the equivalence-class structure induced by attribute set Q. Then, the dependency of attribute set Q on attribute set P,
is a given equivalence class from the equivalence-class structure induced by attribute set Q. Then, the dependency of attribute set Q on attribute set P,  , is given by
, is given by
 (3)
(3)
That is, for each equivalence class 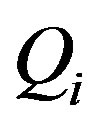 in
in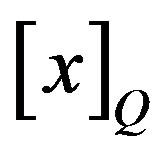 , we add up the size of its lower approximation by the attributes in P, i.e.,
, we add up the size of its lower approximation by the attributes in P, i.e.,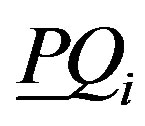 . This approximation (as above, for arbitrary set X) is the number of objects which on attribute set P can be positively identified as belonging to target set
. This approximation (as above, for arbitrary set X) is the number of objects which on attribute set P can be positively identified as belonging to target set . Added across all equivalence classes in
. Added across all equivalence classes in , the numerator above represents the total number of objects which—based on attribute set P—can be positively categorized according to the classification induced by attributes Q. The dependency ratio therefore expresses the proportion (within the entire universe) of such classifiable objects. The dependency
, the numerator above represents the total number of objects which—based on attribute set P—can be positively categorized according to the classification induced by attributes Q. The dependency ratio therefore expresses the proportion (within the entire universe) of such classifiable objects. The dependency  “can be interpreted as a proportion of such objects in the information system for which it suffices to know the values of attributes in P to determine the values of attributes in Q”.
“can be interpreted as a proportion of such objects in the information system for which it suffices to know the values of attributes in P to determine the values of attributes in Q”.
Another, intuitive, way to consider dependency is to take the partition induced by Q as the target class C, and consider P as the attribute set we wish to use in order to “reconstruct” the target class C. If P can completely reconstruct C, then Q depends totally upon P; if P results in a poor and perhaps a random reconstruction of C, then Q does not depend upon P at all.
Thus, this measure of dependency expresses the degree of functional (i.e., deterministic) dependency of attribute set Q on attribute set P; it is not symmetric. The relationship of this notion of attribute dependency to more traditional information-theoretic (i.e., entropic) notions of attribute dependence has been discussed in a number of sources.
The dependency of attribute set Q on attribute set P also be named as the relative importance (with decision attribute d).
3. Decision Making Model
Multi-attribute decision making (MADM) provides a structured approach to decision making. MADM approach requires that the selection be made among decision alternatives described by their attributes. It assumes that the problem has predetermined number of decision alternatives.
There are three generic types of MADM problems as follows:
1) Selection: Given a set of decision alternatives, the selection task involves finding the alternative (or alternatives) judged by the decision maker as the most satisfying.
2) Sorting: It consists of assigning each alternative to one of the predefined criteria. Assignment is often based on relative differences of decision alternatives along a criterion.
3) Ranking: It involves establishing a preference preorder on the set of decision alternatives. The pre-order represents a priority list of the alternatives.
All the three types of MADM problems have been researched by many universities and research institutes. However, most MADM models almost neglected uncertainty or missing values in decision alternatives, which are impact on selection, sorting and ranking.
Here we propose a MADM model to overcome above disadvantages. Selection, sorting and ranking of MADM problems are the same fundamental principles and they are just have different application. So we choose selection of MADM problems as an example to illustrate how to deal with uncertainty or missing values in decision alternatives.
Let support that the decision making system is a complete information system. A complete information system means all decision rules can be found in the rule table. We consider mismatched values in decision alternatives and construct a new MADM model. The steps of decision making are as follows.
Step 1: Obtain information table (information matrix) according to problems described.
Step 2: Obtain decision table from information table by computing weights and RED in rough set theory.
Step 3: Reduce attributes values to obtain clear decision table.
Step 4: Extract decision rules and computer their confidence degree, coverage degree and support degree. Every rule denotes an alternative.
Step 5: Compare a new problem with alternatives and judge through confidence degree, coverage degree and support degree.
4. Example
Suppose Table 1 is an information system, which c1, c2, c3, c4, c5, c6, c7, c8 are conditional attributes and d is decisional attribute [14].
For rough set cannot deal with continuous attribute values, we discrete continuous attribute values follow with rules in Table 2. Table 3 is information system
after discretization.
Table 4 is information system after reduction, which is named decision table.