Quantum Theory Improvement of the Photoelectric Effect on Metals

Amaury de Kertanguy

LERMA, Observatoire de Paris-Meudon Place Jules Janssen, Meudon, France.

DOI: 10.4236/jamp.2022.108165                

Abstract

This paper concerns the full interaction of a flux of photons onto any metal whose extraction potential is known. The photons are described with a full wavefunction, including all states of polarization, and the ejected electrons are considered with their two spin states. The purpose is to give a full theoretical description of the interaction of the photoelectric effect, known since a long time, it verifies that the electron of any peculiar metal can escape if a threshold is met. These wavelengths are accessible for many metals, the photoelectrons exist if the condition: . U₀ is the extraction potential given in eV, these are tabulated. The system wavefunction (electron + photon) a product of the electron free wave and of the photon, taken as , is defined, and the total Ψ(t) is truncated as required by the condition . It is possible to use any combination of polarization states for the photon, with at maximum a mixture of all possible polarizations, which is linear and right and left circular. The method applied takes into account the basic electron photon interaction, the free electron, which is the ejected electron, is described by a free wave, restricted to the first momenta. The quantum theory of the interaction needs to evaluate the integrals: , where r_max is a cut-off parameter to insert to enable finite values of these integrals. The I is calculated on the variables r, θ, φ, and the r³ concerns the radial volume multiplied by the r coming from the dipolar interaction. It follows that using the Fermi golden rule leads to an estimate of the probability of escape of an electron P_ij, assuming that the normalisation factor of the A the electomagnetic vector is . The results for copper metal are given, the probabilty of escape, P_ij has the correct dimension .

Keywords

Photoelectric Effect, Quantum Theory, Electron Photon Interaction

1. Introduction

The interpretation of the photoelectric is historically the first discovery of quanta as explained by Albert Einstein (1905). Extracted electrons from the metal are subject to the law: $h\nu =\frac{hc}{\lambda }\ge U_0$ , where the energy of the photon converted in eV has to be greater than the $U_0$ extraction potential. These potentials are known for most metals. The author proposes to deepen this basic electron photon interaction using all possible states of polarization of photons (J = 1 is the photon spin: thus $g=2\times J+1=3$ . and the two states of the electron: $\sigma =\pm \frac{\hslash }{2}$ . This approach implies at least six states to deal with the photon electron interaction. This interaction is defined using the electromagnetic field $A\left(t\right)$ , the electron is considered as a free wave whose energy and impulse $\stackrel{\to }{K}$ result from the simple energy balance: $h\nu -U_0=\frac{m_e{V}^2}{2}=\frac{{\hslash }^2{K}^2}{2m_e}$ . It is known

that normalizing a free wave for the electron written as: ${\text{e}}^{i\tilde{K}\cdot \tilde{r}}$ is a difficult problem when the r radial coordinate goes to infinity. The results are given for a quantity: $r_{\max }$ , that is the position of the electron over the metal, it is a probability to find the ejected electron at a given place.

This paper shows how to improve the photoelectric effect on the theoretical side, it uses the full photon wavefunction quantum description, dealing with the three states of polarization (or any combination of these), classically the photon exists linearly polarized: $|J=1,M=0\rangle$ , and left circular and right circular

$|J=1,M\pm 1\rangle$ , for what concerns the escape electron, its wavefunction is considered as a free wave, it is not anymore at the metal surface. The electron wavefunction as a free wavefunction has two spin states: $\sigma =\pm \frac{\hslash }{2}$ , the so-called polarized electrons. The useful wavelengths that give rise to the phenomenon of electrons extraction are such that: $\lambda \le {\lambda }_0=\frac{hc}{U_0}$ , this is the basis of the Einstein interpretation of the photoelectric effect and consequently appears the Planck constant. In these early days the quantum field of radiation and the Born interpretation of the existence probability of such particles (electron, photon, proton) are not known, in the Born view, if a wavefunction exists for a particle it should verify: ${\displaystyle {\int }_0^{\infty }}\Psi {\Psi }^{\mathrm{<mo>\; *\; </mo>}}{r}^2\text{d}r\text{d}\Omega =1.$

For a free photon with the basic wavefunction: $\psi =\frac{{\text{e}}^{i\tilde{K}\cdot \tilde{r}}}{\sqrt{V}}$ , integrated on the

whole space variables, the existence probability tends to $\infty$ , this divergence is the major theoretical problem posed by the wave theory of photons in the wave corpuscule duality. If a photon is not absorbed or emitted, the free wave description does not match the Born condition. In our paper, the photon interacts with the electron on the metal surface, thus it is localized enabling a free wave with no divergence when integrated.

2. Describing a Photon by Its Angular Wavefunction

We consider the following angular wavefunction $|J=1,M=\pm 1,0\rangle$ for a photon with its different 3 polarization states, orthogonal to each others. These are spherical harmonics $Y_{l=1}^{m=\pm 1}\left(\theta ,\varphi \right)$ , these give the circular right and circular left the linear is $Y_{l=1}^{m=0}\left(\theta ,\varphi \right)$ . One considers the photon as a boson, thus with ainteger spin $J=1$ , with three independent states.

The following equations describe the photon with all its polarized states with an equal proportion for these states.

$\Psi =a_{-1}|1,-1\rangle +a_0|1,0\rangle +a_1|1,1\rangle$ (1)

$\Psi {\Psi }^{*}={\left|a_{-1}\right|}^2+{\left|a_1\right|}^2+{\left|a_0\right|}^2=1$ (2)

The product $\Psi {\Psi }^{*}=1$ means that the photon exists, with an equal polarization probablility, a photon beam linearly polarized implies $a_{-1}=a_1=0$ . it follows:

$a_{-1}=a_0=a_1=a_{-1}=\frac{1}{\sqrt{3}}$ (3)

In order to precise this wavefunction, it is useful to write:

$H\Psi =E\Psi$ (4)

$H=-i\hslash \frac{\text{d}}{\text{d}t}$ (5)

$H\Psi =\hslash \omega \Psi$ (6)

Therefore the solution for $\Psi$ with $-i\hslash \frac{\text{d}}{\text{d}t}=\hslash \omega \Psi$ , gives $\frac{\text{d}\Psi }{\Psi }=i\omega \text{d}t$ , integrating gives $\log \Psi =i\omega t$ , thus $\Psi \left(t\right)={\text{e}}^{i\omega t}$ , thus verifying the condition $\Psi {\Psi }^{*}=1$ and taking into account the cut in frequencies involved by the threshold: $h{\nu }_0=\hslash {\omega }_0\ge U_0$

$U_0$ is the extraction potential of metals, meaning that the electrons before the illumination are kept inside the metals. The cutting parameter for the frequencies are ${\omega }_0=\frac{U_0}{\hslash }$ , (to obtain homogeinity $U_0$ should be written in Joules). The wavefunction is modified this way:

$\Psi \left(t\mathrm{,}{\omega }_0\right)=UnitStep\left[\omega -{\omega }_0\right]$ (7)

$\Psi \left(t\mathrm{,}{\omega }_0\right)\Psi {\left(t\mathrm{,}{\omega }_0\right)}^{\mathrm{<mo>\; *\; </mo>}}=UnitStep{\left[\omega -{\omega }_0\right]}^2$ (8)

$a_{-1}=a_0=a_1=a_{-1}=\frac{1}{\sqrt{3}}$ (9)

The Mathematica function $UnitStep\left[\omega -{\omega }_0\right]$ is the same as the Heaviside distribution, it means that:

.

Finally including the cutting frequency 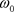(that depends of the irradiated metal), the photon wave function is written down:

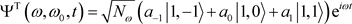(10)

is the number of photons at the frequency.

The factor 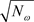insures that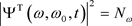, that is the wavefunction for 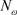photons of the same mode.

It is possible to perform the Fourrier transform of the function: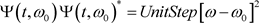

This Fourier transform is:

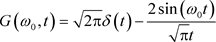(11)

3. The Free Electron Wavefunction

The energy balance of the photoelectric effect is: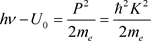. When

the mechanics of the photon electron interaction takes place, the ejected electron obtain an impulse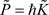, 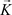serves to build the free wave function ot the electron, that is with the Dirac ket representation: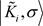, this ket includes the

two possible spin states. Finally the electron wavefunction is:

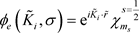(12)

This wavefunction can be developed on partial waves as shown:

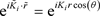(13)

(14)

Else for small impulses, that concerns an electron near the threshold of the ejection mechanism, one can write:

(15)

Spherical Harmonics Description for Kets

First of all setting:, these values mean an equal polarization for each independent states, then the photon wavefunction with is defined by:

(16)

(17)

The full wave function is:

(18)

Explicitly:

(19)

(20)

(21)

4. Quantum Theory of the Interaction Electron Photon

The phenomenon of ejecting an electron from the metal is governed by the dipole operator to a good approximation:, and the energy associated with the interaction mechanism is:

(22)

Since from electromagnetic field theory it is well established that:, with:

, and introducing the normalizing factor:, then

, finally the expression of the interaction energy is:

(23)

(24)

1One obtains the probability for an electron to be ejected from the irradiated metal by the calculation of:

(25)

(26)

(27)

(28)

(29)

5. Evaluation of the Probability of Ejection of an Electron

The probability to evaluate is:.

The oscillating factor disappears because of the squared modulus. The evaluation of the probability already has given theoretical work [1] . For small, thus an electron near the threshold:, a frequency

, then it is easy to write [2] :

(30)

(31)

Making the assumption that the polarization vector can be written as:

(32)

The probability is at the order: (that means)

Impulse K and ejection distance of the electron r both small.

(33)

(34)

These can be calculated.

6. Development of Calculation of the Probabilities

Then simplifies setting:.

(35)

(36)

The spherical harmonics are orthonormal functions, obeying to

It follows that for the development of integrals like:

, thus stays in the evaluation the quantity:

(37)

Using the relation: and . with.

These equations prove that connects only the photon wavefunction with, this probability is evaluated with Mathematica restricting the sum:

,

taking into account 3 partial waves

.

An alternative way to calculate is to introduce the development in series of the bra

. Equation (15)

recalling:

(38)

The squared scalar product serves to estimate the transition probability given by the Fermi golden rule.

For

(39)

(40)

(41)

(42)

7. Results Obtained with Mathematica

The full expression, with the trigonometric functions is:

(43)

integrating on angles gives a good approximation of the dipole operator, with the condition ().

A consequence is that development of, connects all the polarization states of the photon.

Mathematica can be used and give results for these integrals.

To evaluate the probabilities, it is necessary to define the density of states:

or its continuous value [3] .

Using the relation with and, it comes:

(44)

(45)

(46)

(47)

(48)

(49)

with and setting:.

Applying the Fermi golden rule gives for the ejection probability:

(50)

(51)

(52)

(53)

It appears that only connects the ket linked to only one polarization state.

If no preferred direction are inserted in the interaction electron photon interaction:

then is written with the help of:

Considering isotropic polarization states:.

Changing into spherical coordinates gives:

(54)

(55)

It follows that using this development, the scalar product is written: then is written:

(56)

(57)

(58)

It is possible with this development to connect different polarization states. and because

Integrating on the radial variable means:. One deals with an integral that does not converge, when the range is fixed to to the upper limit to, the integral becomes a function of this quantity, the value for V appears in the definition of the electromagnetic field:

(59)

The quantity is integrated with Mathematica using the development.

7.1. Calculations of Integrals Required When Applying the Fermi Golden Rule

Integrating on the radial variable means:. One deals with an integral that does not converge, when the range is fixed to to [3] .

To avoid this divergence, all calculations are done fixing the upper limit to, the integral becomes a function of this quantity, the value for V, included in fac = is defined as and

is developed the maximum number of waves is fixed to lmax = 3 the summed waves function are defined:

(60)

An alternative way to have results for the integrals is to make a Taylor serie:

(61)

(62)

(63)

Changing the spherical harmonics into their trigonometric values:

(64)

(65)

This complete integral diverges when, but still possible to obtain a finite value using an upper limit and modifying the upper integral to with this upper limit and dividing it with:.

The dipole element is integrated easily with Mathematica, then squared to obtain the probability although the radial variable on its domain does not converge, the author uses the a limit.

It is correct to use Taylor series for, this gives at the fourth order development of this quantity ():

(66)

It follows:

(67)

(68)

(69)

The complete integral is obtained performing the integration over and is obtained:

(70)

(These quantities are obtained with Mathematica)

7.2. Mathematical Treatment of the Interaction

It shows that exists a coupling with the, that is with all components of the polarized photons. and thus obtains for the formula:

(71)

To obtain the probability of the electron being released from the metal, that is using the Fermi golden rule: and defining with the relation, the density of free states enables to justify the following integrals.

It is necessary to compute:

(72)

(73)

(74)

Using the well known function properties (see Apendix):

(75)

with thus with homogeneous to the wave vector K. This gives: see Appendix

(76)

(77)

It follows the complete formula for the probability of escape of the electron:

(78)

It is reasonable to reject the factor, because the wave vector cannot be negative.

Defining the factor: where the volume V comes from the electromagnetic is.

Adding the electron spin contribution given by. Finally This leads to the escape probability of electrons in a metal, with a photon flux at the threshold of a peculiar metal is:

(79)

The electron spin wave function for the two states is:

, because of the squared modulus, the spin function gives for, that is the final quantity:

is the same, each of the two electron states gives the same contribution:.

The full expression giving the final form of the formula is: (with)

(80)

Applying the function to the formula Equation (81) gives: and replacing with, it simplifies, dividing by the volume V that gives:

(81)

(82)

(83)

(84)

7.3. Final Formula

Considering the small value of, the greatest term in Equation (81) is it is correct to keep for.

Inserting the values of the constants gives:

(85)

The prevailing term is therefore:.

At this stage, the formula for should have the dimemsion of a probability, instead the upper formula has a dimension:, it appears that this question is exposed in [4] page 1142, formula (2.23).

I thus use the approach of [4] , and this manipulation insures that:

, thus the final formula is now:

(86)

Using MKS units for the constants involved in the formula:

Planck constant, electron mass vacuum permittivity, light velocity, electron charge

Inserting the numerical values of the physical constants gives:

(87)

The idea is to define as:

(88)

Thus the formula with the time t variable and the wave vector is:

(89)

An example is shown using the extraction potential of the copper element: giving these numbers for the extraction potential of copper with the corresponding wavelength:

and the so called pulsation is follows

with these data the final probality of escape of an electron is:

(90)

Figure 1 illustrates the probability of electron escape on a Cu metal surface with the basic condition.

The frequency range is: for the blue graph, that means that the wavelengths associated with the incident photons are shorter than the threshold, thus more energetic compliant with the early Einstein explanation of the photoelectric effect (1905).

Figure 1. Escape probability of an electron (with a number of photons), from a Cu surface with condition of frequecy:, that is:. For different frequency ranges the probability exists with the basic approximation, the probability is, thus very sensible to change in time t (in the graph), the wave vector is.

The Mathematica function is equivalent to the Heaviside function, this assures the conformity of the threshold effect prohibiting wavelengths.

Once the escape probability is defined, the electron current is proportional to, it is possible to write the intensity with its formula:. We can infer:.

8. Conclusions

This paper tackles the photoelectric effect, in a upgraded fashion, it includes the threshold effect that once checked can possibly produce electrons with the condition depending on the choice of the metal.

Recent work [5] , on the extraction potentials of metals or semiconductors called these as work function, part of it, the present paper dealing with photon electron interaction on metal surfaces gives a good quantum approach giving experimental results.

The photon electron interaction is taken to be dipolar, and the bulk of the integration using a free electron wave function, to mix to the photon free wave, is performed with symbolic software Mathematica, with the condition One could say that fast electrons should be near a small, and low electrons could be found at a distance, provided that the condition is fulfilled. It appears in the theoretical part that, all polarization states of the photon can furnish different integrals and it is possible to include different polarization states: that means that coefficients: and describe a linear polarization state, although that circular polarization could be taken on:. For what concerns the integral with the exponential function, that is the electron wave function, there are two approaches: the first

is to develop the,

Mathematica is very efficient to calculate the overlap, of the photon wave function with those of the electron. Another way for the integral leading to the probability is to perform a wavelet calculation that is evaluating.

Then, the sum is restricted to the first momenta that is. This integral is more difficult to perform than in the case of the first approach, the reader can find the integral with the partial waves in Appendix A1.

Finally the aim of this paper is to evaluate the quantity:, concerns the photon wavefunction, and is the electron wavefunction, it is impossible to perform the evaluation of I, with the range but it is possible to evaluate this quantity with the range, making

possible to evaluate I, dividing it by:.

Table 1. Physical constants MKS.

The author suggests that the final formulas the first, involving the frequencies that is

and the second depending on the time t: can be used to perform experiments on different metallic surfaces.

To illustrate these considerations, if, the ejection velocity Vtest is shown in different units of length

, ,

Table 1 summarizes the physical constants used in the calculations.

Appendix A

A.1. Mathematica Full Calculation of L = 0, L = 1, L = 2 Partial Waves

The integral: is:

(91)

(92)

L = 0

(93)

L = 1

(94)

L = 2

(95)

A.2. Using Dirac δ Functions

Using the well known function properties, these are useful relations:

(96)

(97)

It is necessary to apply these basic identities to our problem: first step:

(98)

(99)

(100)

Using the well known function properties, these are useful relations:

One needs to solve:

(101)

(102)

with thus with homogeneous to the wave vector K.

(103)

(104)

(105)

(106)

(107)

NOTES

[1] -e is a positive quantity.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Glasser, M.L. and Bagghi, A. (1976) Theories of Photoemission from Metal Surfaces. Progress in Surface Science, 7, 113-148. https://doi.org/10.1016/0079-6816(76)90003-4
[2]	Dirac, P.A.M. (1982) The Principles of Quantum Mechanics. Oxford University Press, Oxford.
[3]	Messiah, A. (1960) Mecanique Quantique. Physics Today, 13, 50. https://doi.org/10.1063/1.3056824
[4]	Rzazewski, K. and Boyd, R.W. (2004) Equivalence of Interaction Hamiltonians in the Electric Dipole Approximation. Journal of Modern Optics, 51, 1137-1147.
[5]	Kim, J.W. and Kim, A. (2021) Absolute Work Function Measurement by Using Photoelectron Spectroscopy. Current Applied Physics, 31, 52-59. https://doi.org/10.1016/j.cap.2021.07.018