On Maps Preserving the Spectrum on Positive Cones of Operator Algebras

Zhiqin Dang

School of Mathematical Sciences, Qufu Normal University, Qufu, China.

DOI: 10.4236/jamp.2022.105118                

Abstract

We consider the spectrum-preserving maps on positive definite cones of C^*-algebras or von Neumann algebras. We first introduce some basic properties of Jordan isomorphism. Then, we study the additively spectrum preserving property and the multiplicatively spectrum-preserving property, and prove that these maps can be characterized by Jordan isomorphisms between C^*-algebras.

Keywords

Jordan ^*-Isomorphsim, Preserve, Spectrum, C^*-Algebra

1. Introduction

In the research field of operator algebra, preserving problem is one of the hot research directions. Over the years, a large number of mathematicians and researchers have devoted themselves to the study of it ( [1] [2] [3]). There are also many works on preserves of Kubo-Ando means by M. Gaál, G. Nagy, Lei Li, Molnár L., Semrl P. and Liguang Wang ( [4] - [12]). These preserves are characterized by Jordan ^*-isomorphisms.

We now recall the concept and properties of Jordan ${}^{*}$ -isomorphisms that will be used in this paper. We refer to [3] for more properties of Jordan ${}^{*}$ -isomorphisms. Suppose that $\mathcal{A}$ and $\mathcal{B}$ are $C^{*}$ -algebras, a bijective linear map $J\mathrm{<mo>\; :\; </mo>}\mathcal{A}\to \mathcal{B}$ is a Jordan ${}^{*}$ -isomorphism if it satisfies

$J\left(AB+BA\right)=J\left(A\right)J\left(B\right)+J\left(B\right)J\left(A\right),J{\left(A\right)}^{\ast }=J(\; A\; \ast \; )$

for all $A\mathrm{,}B\in \mathcal{A}$. The Jordan ${}^{*}$ -isomorphism $J$ preserves the Jordan triple product, i.e., for any $A\mathrm{,}B\in \mathcal{A}$, we have that

$J\left(ABA\right)=J\left(A\right)J\left(B\right)J\left(A\right)\mathrm{.}$

For any $A\in \mathcal{A}$, $A$ is invertible if and only if $J\left(A\right)$ is invertible and, moreover,

$J{\left(A\right)}^{-1}=J\left(A^{-1}\right).$

In particular, $J$ preserves the spectrum of the elements, i.e.,

$\sigma \left(J\left(A\right)\right)=\sigma (\; A\; )$

for any $A\in \mathcal{A}$. We also have

$J\left(f\left(A\right)\right)=f\left(J(\; A\; )\right)$

for any $A\in {\mathcal{A}}_s$ and continuous real function $f$ on its spectrum. Moreover, $J$ preserves commutativity in both directions, i.e., for any $A\mathrm{,}B\in \mathcal{A}$, we have

$AB=BA\iff J\left(A\right)J\left(B\right)=J\left(B\right)J\left(A\right).$

Finally, for any $A\mathrm{,}B\in {\mathcal{A}}_s$ we have

$A\le B\iff J\left(A\right)\le J\left(B\right),$

and $J$ is an isometry,

$\Vert J\left(A\right)\Vert =\Vert A\Vert \mathrm{,}A\in {\mathcal{A}}_{\text{+}}^{-1}\mathrm{.}$

Let $\mathcal{A}\mathrm{,}\mathcal{B}$ be $C^{*}$ -algebras with the set of all self-adjoint ${\mathcal{A}}_s\mathrm{,}{\mathcal{B}}_s$ respectively. Suppose $\varphi \mathrm{<mo>\; :\; </mo>}{\mathcal{A}}_s\to {\mathcal{B}}_s$ be a surjective map. Molnár in [13] considered the map that satisfies

$\sigma \left(\varphi \left(a\right)+\varphi \left(b\right)\right)=\sigma \left(a+b\right)\mathrm{,}a\mathrm{,}b\in {\mathcal{A}}_s$ (1.1)

and

$\sigma \left(\varphi \left(a\right)\varphi \left(b\right)\right)=\sigma \left(ab\right)\mathrm{,}a\mathrm{,}b\in {\mathcal{A}}_s\mathrm{.}$ (1.2)

He showed that these maps are characterized by Jordan ^*-isomorphism.

In this paper, we would like to consider when there are two maps in (1.1) and (1.2). The results obtained in this generalize Molnár’s works in [13]. Suppose $\varphi \mathrm{<mo>\; :\; </mo>}{\mathcal{A}}_s\to {\mathcal{B}}_s$ and $\psi \mathrm{<mo>\; :\; </mo>}{\mathcal{A}}_s\to {\mathcal{B}}_s$ be surjective maps. Now we consider the following structures

$\sigma \left(\varphi \left(a\right)+\psi \left(b\right)\right)=\sigma \left(a+b\right)\mathrm{,}a\mathrm{,}b\in {\mathcal{A}}_s$

and

$\sigma \left(\varphi \left(a\right)\psi \left(b\right)\right)=\sigma \left(ab\right)\mathrm{,}a\mathrm{,}b\in {\mathcal{A}}_s\mathrm{.}$

In the process of proving the theorem, we describe some lemmas, and then give the results and proofs.

2. Main Results

Now we first give fives lemmas that will use in the proving theorems.

Lemma 2.1. ( [14]) Let $\mathcal{A}\mathrm{,}\mathcal{B}$ be $C^{*}$ -algebras. If 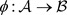is a surjective linear isometry, then it of the form

$\varphi \left(a\right)=uJ\left(a\right),a\in \mathcal{A},$

where $u\in \mathcal{B}$ is a unitary element and 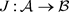is a Jordan ${}^{*}$ -isomorphism.

Lemma 2.2. ( [7]) Let $\mathcal{A}\mathrm{,}\mathcal{B}$ be $C^{*}$ -algebras and let $\varphi \mathrm{<mo>\; :\; </mo>}\mathcal{A}\to \mathcal{B}$ be a bijective linear map which preserves the order in both direction, i.e., satisfies

$a\le b\iff \varphi \left(a\right)\le \varphi \left(b\right)\mathrm{,}a\mathrm{,}b\in {\mathcal{A}}_s\mathrm{.}$

Then $\varphi$ is of the form

$\varphi \left(a\right)=tJ\left(a\right)t^{*},a\in \mathcal{A},$

where $t\in \mathcal{B}$ is an invertible element and $J\mathrm{<mo>\; :\; </mo>}\mathcal{A}\to \mathcal{B}$ is a Jordan ${}^{\mathrm{<mo>\; *\; </mo>}}$ -isomorphism.

Lemma 2.3. ( [13]) Let $\mathcal{A}$ be a von Neumann algebra. Assume $a\in \mathcal{A}$ is a symmetry such that for every symmetry $t\in \mathcal{A}$, the spectrum $\sigma \left(st\right)$ contains only real numbers. Then $s$ is a central symmetry in $\mathcal{A}$.

Lemma 2.4. ( [13]) Let $\mathcal{A}$ be a von Neumann algebra. Pick $a\mathrm{,}b\in {\mathcal{A}}_s$. If $\sigma \left(at\right)=\sigma \left(bt\right)$ holds for all $t\in {\mathcal{A}}_{+}^{-1}$, then we have $a=b$.

Lemma 2.5. ( [9]) Let $\mathcal{A}$ be a $C^{\mathrm{<mo>\; *\; </mo>}}$ -algebra and pick $\forall a\mathrm{,}b\in {\mathcal{A}}_{+}^{-1}$, then

$a\le b\iff \Vert xax\Vert \le \Vert xbx\Vert \mathrm{,}x\in {\mathcal{A}}_{+}^{-1}\mathrm{.}$

The following are the main results obtained in this paper.

Theorem 2.1. Suppose $\mathcal{A}$ and $\mathcal{B}$ are $C^{\mathrm{<mo>\; *\; </mo>}}$ -algebras and $\varphi \mathrm{,}\psi \mathrm{<mo>\; :\; </mo>}{\mathcal{A}}_s\to {\mathcal{B}}_s$ are surjective maps. Then

$\sigma \left(\varphi \left(a\right)+\psi \left(b\right)\right)=\sigma \left(a+b\right)\mathrm{,}a\mathrm{,}b\in {\mathcal{A}}_s\mathrm{,}$

and

$\varphi \left(0\right)=\psi (\; 0\; )$

if and only if there is a Jordan isomorphism $J\mathrm{<mo>\; :\; </mo>}\mathcal{A}\to \mathcal{B}$ such that $\varphi =\phi ={\varphi |}_{{\mathcal{A}}_s}$.

Proof. ( $\Rightarrow$ ) Assume that

$\sigma \left(\varphi \left(a\right)+\psi \left(b\right)\right)=\sigma \left(a+b\right),a,b\in {\mathcal{A}}_s.$

Then we have

$\sigma \left(\varphi \left(a\right)+\psi \left(-a\right)\right)=\sigma \left(a-a\right)=\sigma \left(0\right)=\left\{0\right\},a\in {\mathcal{A}}_s.$

i.e., $\varphi \left(a\right)+\psi \left(-a\right)=0$ and $\varphi \left(0\right)=\psi \left(0\right)=0$. Hence $\psi \left(-a\right)=-\varphi \left(a\right)$. For any $a\mathrm{,}b\in {\mathcal{A}}_s$, we have

$\sigma \left(\varphi \left(a\right)-\varphi \left(b\right)\right)=\sigma \left(\varphi \left(a\right)+\psi \left(-b\right)\right)=\sigma \left(a-b\right),a,b\in {\mathcal{A}}_s.$

Thus $\Vert \varphi \left(a\right)-\varphi \left(b\right)\Vert =\Vert a-b\Vert$ for all $a\mathrm{,}b\in {\mathcal{A}}_s$ and $\varphi \mathrm{<mo>\; :\; </mo>}{\mathcal{A}}_s\to {\mathcal{B}}_s$ is a surjective isometry. It follows from Mazur-Ulam theorem ( [15]) that $\varphi$ is a linear surjective isometry. Then by Lemma 2.1 there exist a Jordan isomorphism $J\mathrm{<mo>\; :\; </mo>}\mathcal{A}\to \mathcal{B}$ and a center symmetry $s\in \mathcal{B}$ such that

$\varphi \left(a\right)=sJ\left(a\right),a\in {\mathcal{A}}_s.$

By the spectrum-preserving property of $\varphi$, put $a=1$, $b=0$, we infer

$\sigma \left(\varphi \left(1\right)+\psi \left(0\right)\right)=\sigma \left(1\right)=\sigma \left(\varphi (\; 1\; )\right)$

and therefore $\varphi \left(1\right)=1$. Since $J\left(1\right)=1$, we have $s=1$. Hence

$\varphi \left(a\right)=J\left(a\right),a\in {\mathcal{A}}_s.$

Since

$\psi \left(a\right)=-\varphi \left(-a\right)=-J\left(-a\right)=J\left(a\right),a\in {\mathcal{A}}_s.$

we have $\psi \left(a\right)=J\left(a\right)=\varphi \left(a\right)$ for $a\in {\mathcal{A}}_s$.

( $\Leftarrow$ ) If $a\mathrm{,}b\in {\mathcal{A}}_s$, then we have

$\sigma \left(\varphi \left(a\right)+\psi \left(b\right)\right)=\sigma \left(J\left(a\right)+J\left(b\right)\right)=\sigma \left(a+b\right).$

This completes the proof. □

In the proof of next theorem we also need the concept of the Thompson metric (see [16]) which we denote by $d_T$. Define

$d_T\left(a,b\right)=\log \max \left\{M\left(a/b\right),M\left(b/a\right)\right\},a,b\in {\mathcal{A}}_{+}^{-1},$

where $M\left(x/y\right)=\inf \left\{\lambda >0:x\le \lambda y\right\}$ for $a\mathrm{,}y\in {\mathcal{A}}_{+}^{-1}$. It also holds:

$d_T\left(a,b\right)=\Vert \log \left(a^{-\frac{1}{2}}b{a}^{-\frac{1}{2}}\right)\Vert ,a,b\in {\mathcal{A}}_{+}^{-1}.$

By Theorem 9 in [16], for every such isometry $\varphi \mathrm{<mo>\; :\; </mo>}{\mathcal{A}}_{+}^{-1}\to {\mathcal{B}}_{+}^{-1}$, there is a Jordan ${}^{\mathrm{<mo>\; *\; </mo>}}$ -isomorphism $J\mathrm{<mo>\; :\; </mo>}\mathcal{A}\to \mathcal{B}$, a center projection $p\in \mathcal{B}$ and a positive invertible element $c\in \mathcal{B}$ such that

$\varphi \left(a\right)=c\left(pJ\left(a\right)+\left(1-p\right)J\left(a^{-1}\right)\right)c,a\in {\mathcal{A}}_{+}^{-1}.$

Theorem 2.2. Let $\mathcal{A}$ and $\mathcal{B}$ be von Neumann algebras. Suppose $\varphi \mathrm{,}\psi \mathrm{<mo>\; :\; </mo>}{\mathcal{A}}_s\to {\mathcal{B}}_s$ be surjective maps. Then

$\sigma \left(\varphi \left(a\right)\psi \left(b\right)\right)=\sigma \left(ab\right),a,b\in {\mathcal{A}}_s$

and

$\varphi \left(1\right)=\psi (\; 1\; )$

if and only if there exists a Jordan isomorphism $J\mathrm{<mo>\; :\; </mo>}\mathcal{A}\to \mathcal{B}$ such that

$\varphi \left(a\right)=\psi \left(a\right)=J\left(a\right),a\in {\mathcal{A}}_S.$

Proof. ( $\Rightarrow$ ) Suppose $\varphi$ and $\psi$ satisfy $\sigma \left(\varphi \left(a\right)\psi \left(b\right)\right)=\sigma \left(ab\right)$ and $\varphi \left(1\right)=\psi \left(1\right)$. Let $a=b=1$ and we have

$\sigma \left(\varphi \left(1\right)\psi \left(1\right)\right)=\sigma \left(\varphi {\left(1\right)}^2\right)=\sigma \left(1^2\right)=\left\{1\right\}.$

This implies that $\varphi \left(1\right)=\psi \left(1\right)=1$. By Lemma 2.3, $\varphi \left(1\right)$ is a central symmetry. Then it follows that $\varphi$ and $\psi$ preserve the spectrum. In particular, we obtain that $\varphi$ and $\psi$ maps ${\mathcal{A}}_{+}^{-1}$ onto ${\mathcal{B}}_{+}^{-1}$. For any $a\in {\mathcal{A}}_{+}^{-1}$, we have

$\begin{array}{c}\left\{1\right\}=\sigma \left(1\right)=\sigma \left(a{a}^{-1}\right)\\ =\sigma \left(\varphi \left(a\right)\psi \left(-a\right)\right)\\ =\sigma \left(\varphi {\left(a\right)}^{\frac{1}{2}}\psi \left(a^{-1}\right)\varphi {\left(a\right)}^{\frac{1}{2}}\right)\end{array}$

and this implies that $\varphi {\left(a\right)}^{\frac{1}{2}}\psi \left(a^{-1}\right)\varphi {\left(a\right)}^{\frac{1}{2}}=1$, i.e., $\psi \left(a^{-1}\right)=\varphi \left(a\right)$. If $a\mathrm{,}b\in {\mathcal{A}}_{+}^{-1}$, we get

$\begin{array}{c}\sigma \left(\varphi {\left(a\right)}^{-\frac{1}{2}}\varphi \left(b\right)\varphi {\left(a\right)}^{-\frac{1}{2}}\right)=\sigma \left(\varphi \left(b\right)\varphi {\left(a\right)}^{-1}\right)=\sigma \left(\varphi \left(b\right)\psi \left(a^{-1}\right)\right)\\ =\sigma \left(b{a}^{-1}\right)=\sigma \left(a^{-\frac{1}{2}}b{a}^{-\frac{1}{2}}\right).\end{array}$

By the definition of Thompson metric, this implies that $\varphi$ is a surjective Thompson isometry from ${\mathcal{A}}_{+}^{-1}$ onto ${\mathcal{B}}_{+}^{-1}$.

Since for all $a\mathrm{,}b\in {\mathcal{A}}_{+}^{-1}$ and all real numbers $\lambda$, we have

$\begin{array}{c}\sigma \left(\left(\lambda \varphi \left(a\right)\right)\psi \left(b\right)\right)=\lambda \sigma \left(\varphi \left(a\right)\psi \left(b\right)\right)=\lambda \sigma \left(ab\right)\\ =\sigma \left(\left(\lambda a\right)b\right)=\sigma \left(\varphi \left(\lambda a\right)\psi \left(b\right)\right).\end{array}$

It follows from Lemma 2.4 that $\varphi$ is also homogeneous. Hence $\varphi$ is a Thompson isometry. By Theorem 9 in [16] that there exist a Jordan isomorphism $J\mathrm{<mo>\; :\; </mo>}\mathcal{A}\to \mathcal{B}$ such that $\varphi \left(a\right)=J\left(a\right)$ holds for all $a\in {\mathcal{A}}_{+}^{-1}$. We need to show that $\varphi \left(a\right)=J\left(a\right)$ for all $a\in {\mathcal{A}}_s$.

If $b\in {\mathcal{A}}_{+}^{-1}$, then we have

$\psi \left(b\right)=\varphi {\left(b^{-1}\right)}^{-1}=J{\left(b^{-1}\right)}^{-1}=J\left(b\right).$

For any $a\in {\mathcal{A}}_s$ and arbitrary $b\in {\mathcal{A}}_{+}^{-1}$, we have

$\sigma \left(J^{-1}\left(\varphi \left(a\right)\right)b\right)=\sigma \left(J^{-1}\left(\varphi \left(a\right)\right)J^{-1}\psi \left(b\right)\right)=\sigma \left(ab\right),$

and then Lemma 2.4 implies that $J^{-1}\left(\varphi \left(a\right)\right)=a$, i.e., $\varphi \left(a\right)=J\left(a\right)$, $a\in {\mathcal{A}}_s$. For any $b\in {\mathcal{A}}_{+}^{-1}$ and $a\in {\mathcal{A}}_s$, we have

$\begin{array}{c}\sigma \left(J^{-1}\left(\psi \left(a\right)\right)b\right)=\sigma \left(J^{-1}\left(\psi \left(a\right)\right)J^{-1}\left(\varphi \left(b\right)\right)\right)=\sigma \left(\psi \left(a\right)\varphi \left(b\right)\right)\\ =\sigma \left(\varphi \left(b\right)\psi \left(a\right)\right)=\sigma \left(ba\right)=\sigma \left(ab\right).\end{array}$

Hence $J^{-1}\circ \psi \left(a\right)=a$ and $\psi \left(a\right)=J\left(a\right)$ for all $a\in {\mathcal{A}}_s$.

( $\Leftarrow$ ) For $a\mathrm{,}b\in {\mathcal{A}}_s$, we have

$\sigma \left(\varphi \left(a\right)\psi \left(b\right)\right)=\sigma \left(J\left(a\right)J\left(b\right)\right)=\sigma \left(ab\right)\mathrm{.}$

This completes the proof. □

Let $\mathcal{A}$ be a standard $C^{\mathrm{<mo>\; *\; </mo>}}$ -algebra acting on a Hilbert space $\mathcal{H}$. Suppose $a\mathrm{,}b\in {\mathcal{A}}_s$, such that $\sigma \left(at\right)=\sigma \left(bt\right)$ holds for all $t\in {\mathcal{A}}_{+}^{-1}$. Pick $p\in \mathcal{A}$ and $\left({\lambda }_n\right)\to 0$, we have $\sigma \left(a\left({\lambda }_n\cdot 1+p\right)\right)=\sigma \left(b\left({\lambda }_n\cdot 1+p\right)\right)$. By the Corollary 3.4.5 in [17], $\sigma \left(ap\right)=\sigma \left(bp\right)$ holds for every rank-one projective $p$. Then for every unit vector $\xi$ in $\mathcal{H}$, we have $\langle a\xi ,\xi \rangle =\langle b\xi ,\xi \rangle$ and therefore $a=b$. Now we can prove the following result.

Theorem 2.3. Let $\mathcal{A}\mathrm{,}\mathcal{B}$ be standard $C^{\ast }$ -algebras. Suppose $\mathcal{A}$ is acting on the Hilbert space $\mathcal{H}$ and $\mathcal{B}$ is acting on the Hilbert space $\mathcal{K}$. Let $\varphi \mathrm{,}\psi \mathrm{<mo>\; :\; </mo>}{\mathcal{A}}_s\to {\mathcal{B}}_s$ be surjective maps. Then

$\sigma \left(\varphi \left(a\right)\psi \left(b\right)\right)=\sigma \left(ab\right)\mathrm{,}a\mathrm{,}b\in {\mathcal{A}}_s$

and

$\varphi \left(1\right)=\psi (\; 1\; )$

if and only if there exist a constant $\lambda \in \left\{-\mathrm{1,1}\right\}$ and either a unitary or an antiunitary operator $u\mathrm{<mo>\; :\; </mo>}\mathcal{H}\to \mathcal{K}$ such that

$\varphi \left(a\right)=\psi \left(a\right)=\lambda ua{u}^{\ast },a\in {\mathcal{A}}_s.$

Proof. ( $\Rightarrow$ ) Suppose that $\varphi \mathrm{,}\psi \mathrm{<mo>\; :\; </mo>}{\mathcal{A}}_s\to {\mathcal{B}}_s$ are surjective maps with

$\sigma \left(\varphi \left(a\right)\psi \left(b\right)\right)=\sigma \left(ab\right),a,b\in {\mathcal{A}}_s.$

For vectors $\xi \mathrm{,}\eta$ in $\mathcal{H}$, we denote the rank one operator $\xi \otimes \eta$ defined by $\left(\xi \otimes \eta \right)\left(v\right)=\langle v\mathrm{,}\eta \rangle \xi$, $v\in \mathcal{H}$. We show that $\varphi$ is injective. If $a\mathrm{,}b\in {\mathcal{A}}_s$, such that $\varphi \left(a\right)=\varphi \left(b\right)$. Then for every $c\in {\mathcal{A}}_s$ that

$\sigma \left(ac\right)=\sigma \left(\varphi \left(a\right)\psi \left(c\right)\right)=\sigma \left(\varphi \left(b\right)\varphi \left(c\right)\right)=\sigma \left(bc\right).$

For $\forall c\in \xi \otimes \xi$, where $\xi \in \mathcal{H}$ is an arbitrary vector and $\Vert \xi \Vert =1$, then we have

$\sigma \left(a\left(\xi \otimes \xi \right)\right)=\sigma \left(b\left(\xi \otimes \xi \right)\right)\mathrm{.}$

Thus $\langle a\xi \mathrm{,}\xi \rangle =\langle b\xi \mathrm{,}\xi \rangle$ and therefore $a=b$. For the self-adjoint element $\varphi \left(1\right)$, we have

$\sigma \left(\varphi {\left(1\right)}^2\right)=\sigma \left(1\right)=\left\{1\right\},$

thus $\varphi {\left(1\right)}^2=1$ and $s=\varphi \left(1\right)$ is a symmetry.

Now we show that $s=\pm 1$. Since

$\sigma \left(s\psi \left(b\right)\right)=\sigma \left(\varphi \left(1\right)\psi \left(b\right)\right)=\sigma \left(b\right),b\in {\mathcal{A}}_s,$

so $\sigma \left(st\right)$ is real for every $t\in {\mathcal{B}}_s$. Suppose $s\ne \pm 1$. Then there is a basis $\left\{{\xi }_{\alpha }\mathrm{,}{\eta }_{\beta }\right\}$ in the Hilbert space $\mathcal{H}$ such that

$s={\displaystyle \underset{\alpha }{\sum }}{\xi }_{\alpha }\otimes {\xi }_{\alpha }-{\displaystyle \underset{\beta }{\sum }}{\eta }_{\beta }\otimes {\eta }_{\beta },$

where neither of these sums is zero. Pick $\xi \in \left\{{\xi }_{\alpha }\right\}$ and $\eta \in \left\{{\eta }_{\beta }\right\}$. Define

$t=i\left(\xi \otimes \eta -\eta \otimes \xi \right).$

Then $t\in {\mathcal{B}}_s$ and $\sigma \left(st\right)=\left\{-i,i\right\}$, that’s a contradiction. It follows that $\varphi \left(1\right)=\pm 1$. If $\varphi \left(1\right)=1$, we have $\sigma \left(\varphi \left(a\right)\right)=\sigma \left(\varphi \left(a\right)\varphi \left(1\right)\right)=\sigma \left(a\right)$ for every $a\in {\mathcal{A}}_s$, and $\varphi$ maps ${\mathcal{A}}_{+}^{-1}$ onto ${\mathcal{B}}_{+}^{-1}$. Thus $\varphi$ is a surjective Thompson isomorphism from ${\mathcal{A}}_{+}^{-1}$ onto ${\mathcal{B}}_{+}^{-1}$. It follows that there is a Jordan ${}^{\mathrm{<mo>\; *\; </mo>}}$ -isomorphism $J\mathrm{<mo>\; :\; </mo>}\mathcal{A}\to \mathcal{B}$ such that

$\varphi \left(a\right)=J\left(a\right),a\in {\mathcal{A}}_s.$

By the result of Herstein [10], $J$ is either a ${}^{\mathrm{<mo>\; *\; </mo>}}$ -isomorphism or a ${}^{\mathrm{<mo>\; *\; </mo>}}$ -antiisomorphism. And from [3], we have either a unitary operator $u\mathrm{<mo>\; :\; </mo>}\mathcal{K}\to \mathcal{H}$ such that

$J\left(a\right)=ua{u}^{*},a\in \mathcal{A},$

or an antiunitary operator $u\mathrm{<mo>\; :\; </mo>}\mathcal{K}\to \mathcal{H}$ such that

$J\left(a\right)=u{a}^{*}{u}^{*},a\in \mathcal{A}.$

The map $J^{-1}\circ \varphi \mathrm{<mo>\; :\; </mo>}\mathcal{A}\to \mathcal{A}$ satisfies

$\sigma \left(\varphi \left(a\right)\psi \left(b\right)\right)=\sigma \left(ab\right),a,b\in {\mathcal{A}}_s,$

and it equals the identity on ${\mathcal{A}}_{+}^{-1}$. If $a\in {\mathcal{A}}_s\mathrm{,}b\in {\mathcal{A}}_s^{-1}$, we have

$\sigma \left(J^{-1}\left(\varphi \left(a\right)\right)b\right)=\sigma \left(J^{-1}\left(\varphi \left(a\right)\right)J^{-1}\left(\psi \left(b\right)\right)\right)=\sigma \left(\varphi \left(a\right)\psi \left(b\right)\right)=\sigma \left(ab\right).$

So $J^{-1}\left(\varphi \left(a\right)\right)=a$, i.e., $J\left(a\right)=\varphi \left(a\right)$. For any $a\in {\mathcal{A}}_s$, we get

$\sigma \left(\psi \left(b\right)\varphi \left(a\right)\right)=\sigma \left(ab\right),a,b\in {\mathcal{A}}_s.$

Therefore, $\psi \left(a\right)=J\left(a\right)$.

( $\Leftarrow$ ) For $a\mathrm{,}b\in {\mathcal{A}}_s$, we have

$\begin{array}{c}\sigma \left(\varphi \left(a\right)\psi \left(b\right)\right)=\sigma \left(\lambda ua{u}^{\ast }\lambda ub{u}^{\ast }\right)\\ =\sigma \left({\lambda }^{2}uab{u}^{\ast }\right)=\sigma \left(uab{u}^{\ast }\right)\\ =\sigma \left(ab\right).\end{array}$

This completes the proof. □

The following characterization of the order of operators is needed in the proof of Theorem 2.4.

Theorem 2.4. Let $\mathcal{A}$ and $\mathcal{B}$ be two $C^{\mathrm{<mo>\; *\; </mo>}}$ -algebras and $\varphi \mathrm{<mo>\; :\; </mo>}{\mathcal{A}}_{+}^{-1}\to {\mathcal{A}}_{+}^{-1}$ be a surjective map. Then

$\sigma \left(\varphi \left(a\right)\varphi \left(b\right)\varphi \left(a\right)\right)=\sigma \left(aba\right)\mathrm{,}a\mathrm{,}b\in {\mathcal{A}}_{+}^{-1}\mathrm{,}$

if and only if there is a Jordan ${}^{\mathrm{<mo>\; *\; </mo>}}$ -isomorphism $J\mathrm{<mo>\; :\; </mo>}\mathcal{A}\to \mathcal{B}$ such that $\varphi \left(a\right)=J\left(a\right)$ for every $a\in {\mathcal{A}}_{+}^{-1}$.

Proof. ( $\Rightarrow$ ) Suppose $\varphi \mathrm{<mo>\; :\; </mo>}{\mathcal{A}}_{+}^{-1}\to {\mathcal{A}}_{+}^{-1}$ is a surjective map satisfies

$\sigma \left(\varphi \left(a\right)\varphi \left(b\right)\varphi \left(a\right)\right)=\sigma \left(aba\right)\mathrm{,}a\mathrm{,}b\in {\mathcal{A}}_{+}^{-1}\mathrm{.}$

First we prove that $\varphi$ preserves the order in both directions. From the Lemma 2.5, for $\forall a\mathrm{,}b\in {\mathcal{A}}_{+}^{-1}$, we have

$\begin{array}{l}a\le b\iff \Vert xax\Vert \le \Vert xbx\Vert ,\forall x\in {\mathcal{A}}_{+}^{-1}\\ \iff \underset{\lambda \in \sigma \left(xax\right)}{\sup }\left|\lambda \right|\le \underset{\mu \in \sigma \left(xbx\right)}{\sup }\left|\mu \right|\\ \iff \underset{\lambda \in \sigma \left(\varphi \left(x\right)\varphi \left(a\right)\varphi \left(x\right)\right)}{\sup }\left|\lambda \right|\le \underset{\mu \in \sigma \left(\varphi \left(x\right)\varphi \left(b\right)\varphi \left(x\right)\right)}{\sup }\left|\mu \right|\\ \iff \Vert \varphi \left(x\right)\varphi \left(a\right)\varphi \left(x\right)\Vert \le \Vert \varphi \left(x\right)\varphi \left(b\right)\varphi \left(x\right)\Vert \\ \iff \varphi \left(a\right)\le \varphi \left(b\right).\end{array}$

Thus $\varphi$ is an order isomorphism.

Next to prove that $\varphi$ is positive homogeneous. If $t>0$, $a\in {\mathcal{A}}_{+}^{-1}$, then for every $x\in {\mathcal{A}}_{+}^{-1}$, we have

$\begin{array}{c}\Vert \varphi \left(x\right)\varphi \left(ta\right)\varphi \left(x\right)\Vert =\sup \left\{\left|\lambda \right|:\lambda \in \sigma \left(\varphi \left(x\right)\varphi \left(ta\right)\varphi \left(x\right)\right)\right\}\\ =\sup \left\{\left|\lambda \right|:\lambda \in \sigma \left(xtax\right)\right\}\\ =t\sup \left\{\left|\mu \right|:\mu \in \sigma \left(xax\right)\right\}=t\Vert xax\Vert \\ =t\Vert \varphi \left(x\right)\varphi \left(a\right)\varphi \left(x\right)\Vert =\Vert \varphi \left(x\right)\left(t\varphi \left(a\right)\right)\varphi \left(x\right)\Vert .\end{array}$

i.e., $\varphi \left(ta\right)=t\varphi \left(a\right)$. Since $\sigma \left(\varphi {\left(1\right)}^3\right)=\sigma \left(1\right)=\left\{1\right\}$, we have $\varphi \left(1\right)=1$. Therefore by Lemma 2.2, there is a Jordan ${}^{\mathrm{<mo>\; *\; </mo>}}$ -isomorphism $J\mathrm{<mo>\; :\; </mo>}\mathcal{A}\to \mathcal{B}$ such that

$\varphi \left(a\right)=J\left(a\right)\mathrm{,}a\in {\mathcal{A}}_{+}^{-1}\mathrm{.}$

( $\Leftarrow$ ) For $a\mathrm{,}b\in {\mathcal{A}}_{+}^{-1}$, we have

$\sigma \left(\varphi \left(a\right)\varphi \left(b\right)\varphi \left(a\right)\right)=\sigma \left(J\left(a\right)J\left(b\right)J\left(a\right)\right)=\sigma \left(J\left(aba\right)\right)=\sigma \left(aba\right).$

This completes the proof. □

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Kubo, F. and Ando, T. (1980) Means of Positive Linear Operators. Mathematische Annalen, 246, 205-224. https://doi.org/10.1007/BF01371042
[2]	Li, C.K. and Tsing, N.K. (1992) Linear Preserver Problems: A Brief Introduction and Some Special Techniques. Linear Algebra and Its Applications, 162-164, 217-235. https://doi.org/10.1016/0024-3795(92)90377-M
[3]	Molnár, L. (2007) Selected Preserver Problems on Algebraic Structures of Linear Operators and on Function Spaces. Lecture Notes in Mathematics, Vol. 1985, Springer, Berlin, 236.
[4]	Gaál, M. and Nagy, G. (2018) A Characterization of Unitary-Antiunitary Similarity Transformations via Kubo-Ando Means. Analysis Mathematica, 45, 311-319. https://doi.org/10.1007/s10476-018-0401-z
[5]	Gaal, M. (2018) Norm-Additive Maps on the Positive Definite Cone of a C-Algebra. Results in Mathematics, 73, Article No. 151. https://doi.org/10.1007/s00025-018-0916-4
[6]	Geher, G.P. (2018) Symmetries of Projective Spaces and Spheres. International Mathematics Research Notices, 2020, 2205-2240. https://doi.org/10.1093/imrn/rny100
[7]	Kadison, R.V. (1952) A Generalized Schwarz Inequality and Algebraic Invariants for Operator Algebras. Annals of Mathematics, 56, 494-503. https://doi.org/10.2307/1969657
[8]	Li, L., Molnár, L. and Wang, L. (2020) On Preserves Related to the Spectral Geometric Mean. Linear Algebra and Its Applications, 610, 647-672. https://doi.org/10.1016/j.laa.2020.10.014
[9]	Molnár, L. (2020) Jordan Isomorphisms as Preservers. In: Linear and Multilinear Algebra and Function Spaces, Contemporary Mathematics, Vol. 750, American Mathematical Society, Providence. https://doi.org/10.1090/conm/750/15102
[10]	Palmer, T.W. (1996) Banach Algebras and the General Theory of C-algebras. Volume I: Algebras and Banach Algebras. Mathematical Gazette, 80, 547-553. https://doi.org/10.1017/CBO9781107325777
[11]	Semrl, P. (2017) Order Isomorphisms of Operator Intervals. Integral Equations and Operator Theory, 89, 1-42. https://doi.org/10.1007/s00020-017-2395-5
[12]	Sourour, A.R. (1996) Invertibility Preserving Linear Maps on L(X). Transactions of the American Mathematical Society, 348, 13-30. https://doi.org/10.1090/S0002-9947-96-01428-6
[13]	Molnár, L. (2020) Spectral Characterization of Jordan-Segal Isomorhpisms of Quantum Observables. Journal of Operator Theory, 83, 179-195.
[14]	Kadison, R.V. (1994) Isometries of Operator Algebras. Journal of Functional Analysis, 119, 138-170. https://doi.org/10.1006/jfan.1994.1006
[15]	Molnár, L. (2015) General Mazur-Ulam Type Theorems and Some Applications. In: Arendt, W., Chill, R. and Tomilov, Y., Eds., Operator Semigroups Meet Complex Analysis, Harmonic Analysis and Mathematical Physics, Advances and Applications, Vol., 250, Springer International Publishing, Berlin, 311-342. https://doi.org/10.1007/978-3-319-18494-4_21
[16]	Hatori, O. and Molnár, L. (2014) Isometries of the Unitary Groups and Thompson Isometries of the Spaces of Invertible Positive Elements in C-algebras. Journal of Mathematical Analysis and Applications, 409, 158-167. https://doi.org/10.1016/j.jmaa.2013.06.065
[17]	Aupetit, B. (1991) A Primer on Spectral Theory. Springer-Verlag, New York.