The Deny Proof of the Palindrome Number Conjecture

Maoze Wang¹, Zhenxiang He², Meiyi Wang³

¹Lanzhou Institute of Technology, Lanzhou, China.
²School of Cyberspace Security, Gansu Politics and Law College, Lanzhou, China.
³Beijing Forestry University, Beijing, China.

DOI: 10.4236/apm.2022.124026                

Abstract

Palindrome number conjecture: Take any non-palindromic natural number with two or more digits, add its inverse ordinal number, continue to use the inverted number of sum plus sum, repeat this process continuously. After a finite number of operations, a palindrome number must be obtained. We firstly give out several definitions: The pure-single-digit-of-sum is the number of single digits that only count the sum of two numbers of the same digit in the vertical operation of addition, which is referred to as pure single digit for short, denoted by g. The pure-carry-digit-of-sum is the carry digit that only counts the sum of two numbers in the same bit in the vertical operation of addition. It is a special number composed of only 1 and 0, which is represented by j'. The complement-0-carry-digit-of-sum is to supplement a 0 on the last side of j' according to the rule of adding bits, which is denoted by j. Therefore, in the addition operation, the sum of any natural number and its inverse ordinal number is divided into two parts: g and j. Then, the characteristics of g and j are characterized by the following two theorems: Theorem 1: As all the numbers in j are 0, j is the palindrome number; As the numbers in j are not all 0, j is not a palindrome number. Theorem 2: The sum of any palindrome number H and any non-palindrome j number must be a non-palindrome number. Then we proved the palindrome number conjecture is not correct by using the above two theorems.

Keywords

Palindrome Number, Palindrome Number Conjecture, Inverse Number, Symmetry, Pure-Single-Digit, Pure-Carry-Digit, Complement-0-Carry-Digit

1. Introduction

A natural number, if read from left to right is exactly the same as read from right to left, we call this number a palindrome number, symmetric number, reflexive number, or salazard number.

The palindromes within 1000 are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 22, …, 989, 999. There are 109 palindromes in total.

Reverse-order-number is the number opposite to the number (code) of a natural number. For example, the reverse-order-number of 12 is 21, the reverse-order-number of 123 is 321, the reverse-order-number of 150 is 051, the reverse-order-number of 1500 is 0051, the reverse-order-number of 3658 is 8563. The inverted number of single digits 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9 is still itself. For example, the reverse-order-number of 0 is 0, and reverse-order-number of 9 is 9. 015 and 0015 cannot be omitted as 15.

If a natural number is recorded as p and its inverse number is recorded as q, then the inverse number of q is p, then p and q are reciprocal numbers. We call p and q a pair of inverse numbers. From the definition, a digit number is equal to the digit number of its inverse number.

Palindrome number conjecture: Take any non-palindromic natural number with two or more digits, add its inverse ordinal number, continue to use the inverted number of sum plus sum, repeat this process continuously. After a finite number of operations, a palindrome number must be obtained.

For example, if 7299 is taken, the inverse number is 9927, and the two numbers are added: 7299 + 9927 = 17,226; and then add its reverse order number: 17,226 + 62,271 = 79,497, 79,497 is a palindrome number.

Most natural numbers become palindromes through this calculation. “At present, the proven conclusions are:

1) All single and two digits can converge to one palindrome number after finite step iteration;

2) 80% of the numbers less than 10,000 can converge to palindromes within 4 steps;

3) 90% of the numbers can converge to palindromes within 7 steps [1] .

Has been calculated, 97.5% of the numbers less than 10,000 can converge to palindromes within 24 steps.

“Palindrome number conjecture is a famous mathematical problem, especially 196. It has not been proved whether it is Lychrel number (Note: those numbers that do not meet the palindrome number conjecture are called Lychrel numbers) [1] .” “196 has been calculated 100,000 times and the number has been ‘upgraded’ to 21,000 bits. Among the first 100,000 integers, there are 5996 numbers like 196, and 196 is the smallest one [2] .”

“It is reported that someone has added 50,000 steps in reverse order to 196, and there is still no palindrome number. This mathematical conjecture has not been proved [3] .”

In 1938, before the advent of the electronic computer, the American mathematician D. Lehmer (1905-1991) calculated step 73 and obtained a 35 bit sum without forming a “palindrome number”. So far, the mathematics lovers who challenge this problem have never stopped. With the development of computer technology, enthusiasts continue to write different programs to challenge this problem. According to the author’s latest survey, W.V. landingham, a leading soldier, had calculated 6.99 million steps in 2006, February and obtained a sum of more than 289 million bits. The result between them has not yet appeared as “palindromes” [4] .

89’s “palindrome number path” is particularly long. You won’t get the palindrome number 8813200023188 until step 24.

In addition, a world record on the number of steps required to reach the “palindrome number” is introduced. It is a 19 digit number 1186060307891929990. It takes 261 steps to calculate the palindrome number. It was discovered by Jason Doucete’s algorithm and program on November 30, 2005 [5] .

The opposite side of the palindrome number conjecture is called “Lychrel numbers conjecture”, that is, there is always a positive integer. According to the operating rules of the palindrome number conjecture, no matter how many times you add it, you still can’t get a palindrome number. The palindrome number conjecture is proved, which also proves that the “Lychrel numbers conjecture” is correct.

2. Main Results

The whole process includes three parts. Part 1 includes the content of palindrome number conjecture and seven definitions. Part 2 are theorem 1 and theorem 2 and their proofs. Part 3 is the summary proof. Using theorem 1 and theorem 2, it is proved that the palindrome number conjecture is not correct, and some counter examples are given.

Part 1

Palindrome number conjecture: Take any natural number with two or more numbers, which natural number is not a palindrome, add its inverse number, if you can’t get the palindrome number, continue to use the inverted number of sum plus sum, repeat this process continuously. After a finite number of operations, a palindrome number must be obtained.

We firstly give several definitions:

Let a natural number be $r_1{r}_2\cdots r_{k-1}{r}_k$ ( $k\in Z^{+}$), and denoted it with p, that is, $p=r_1{r}_2\cdots r_{k-1}{r}_k$ , then the inverse number of p is $r_k{r}_{k-1}\cdots r_2{r}_1$ , denote it with q, that is, $q=r_k{r}_{k-1}\cdots r_2{r}_1$ , so p and q are reciprocal numbers. We call p and q a pair of inverse numbers. It can be seen that the digits of p and q are equal. We denote the digits of p and q digits with $w_p$ and $w_q$ respectively, then $w_p=w_q$ .

In order to study the special needs of the problem, this paper temporarily stipulates that 0 in any position cannot be omitted. For example, the inverse number of 1500 must be written as 0051, and it cannot be written as 51 after 0.

Definition 1: Two-numbers-in-the-same-position are $r_i$ ( $k\in Z^{+}$ , $i=1,2,\cdots ,k-1,k$) in the addend p and $r_{k-i+1}$ ( $k\in Z^{+}$ , $i=1,2,\cdots ,k-1,k$) in the addend q.

$r_i+r_{k-i+1}$ means to sum the addend $r_i$ to the addend $r_{k-i+1}$ from low bit to high bit one by one.

$r_i+r_{k-i+1}=j_{k-i+1}{g}_{k-i+1}$ ( $k\in Z^{+}$ , $i=1,2,\cdots ,k-1,k$ ; $j_{k-i}=0,1$ ; $g_{k-i+1}=0,1,2,3,4,5,6,7,8,9$).

$j_{k-i}$ is the carry of $r_i+r_{k-i+1}$ , that’s ten digits, and $g_{k-i+1}$ is the single digit of $r_i+r_{k-i+1}$ .

Definition 2: Addition of p and q is expressed as $p\oplus q$ , which is to perform the following operations:

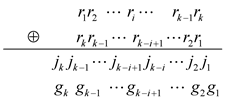
Definition 3: Pure-single-digit-of-sum is the number $r_i$ ( $i=1,2,\cdots ,k-1,k$) and $r_{k-i+1}$ ( $k\in Z^{+}$) in $p\oplus q$ , which is successively arranged by the single digit $g_{k-i+1}$ of the sum of two homologous numbers $g_k{g}_{k-1}\cdots g_{k-i+1}\cdots g_2{g}_1$ .

We abbreviate the pure-single-digit-of-sum as pure-single-digits, expressed by g, then

$g=g_k{g}_{k-1}\cdots g_{k-i+1}\cdots g_2{g}_1$ .

Since the addend $r_i$ and the addend $r_{k-i+1}$ are a pair of inverse ordinal numbers, in the pure single digits of the sum, according to the (addition exchange law) commutative law of addition: $a+b=b+a$ , it can be seen that with the center as the symmetry point, the two corresponding numbers on the left and right have symmetry, so any g is a palindrome number.

Definition 4: Pure-carry-digit-of-sum is the number $j_k{j}_{k-1}\cdots j_{k-i+1}{j}_{k-i}\cdots j_2{j}_1$ in $p\oplus q$ , which is formed by the carry number j of the sum of two numbers $r_i$ ( $k\in Z^{+}$ , $i=1,2,\cdots ,k-1,k$) and $j_{k-i}$ in the same position (starting from right to left, the ( $k-i+1$)-th digit) ( $i=1,2,\cdots ,k-1,k$).

As $r_i+r_{k-i+1}<10$ , $j_{k-i}=0$ ;

As $r_i+r_{k-i+1}\ge 10$ , $j_{k-i}=1$ .

We abbreviate the pure-carry-digit-of-sum as the pure-carry-digit, which is denoted by j', then

$j^{\prime }=j_k{j}_{k-1}\cdots j_{k-i+1}{j}_{k-i}\cdots j_2{j}_1$ .

$j_k{j}_{k-1}\cdots j_{k-i+1}{j}_{k-i}\cdots j_2{j}_1$ and $g_k{g}_{k-1}\cdots g_{k-i+1}\cdots g_2{g}_1$ are one-to-one correspondence, g is a palindrome number, so any j' is a palindrome number.

Definition 5: Complement-0-carry-digit-of-sum is to add a 0 to the last side of the pure carry j' according to the rule of bit alignment during addition operation. The 0 after j' and j' are collectively referred to as the complement 0 carry of sum.

We abbreviate the complement-0-digit-of-sum as the complement-0-digit, which is denoted by j, that is, $j=j^{\prime }0$ , then

$j=j_k{j}_{k-1}\cdots j_{k-i+1}{j}_{k-i}\cdots j_2{j}_{1}0$ .

Special emphasis: the last digit of j is always 0, any other 0 in j is meaningful and cannot be omitted.

Definition 6: Vertical operation of $p\oplus q$ as:

In the above formula, the rule of adding two numbers in the same position is the same as our usual addition.

Definition 7: Horizontal type operation of $p\oplus q$ as:

$\begin{array}{c}p\oplus q=r_1{r}_2\cdots r_{k-1}{r}_k+r_k{r}_{k-1}\cdots r_2{r}_1\\ =j_k{j}_{k-1}\cdots j_i\cdots j_2{j}_{1}0+g_k{g}_{k-1}\cdots g_{k-i+1}\cdots g_2{g}_1\end{array}$

We denote the digit of g with $w_g$ , according to $r_i+r_{k-i+1}=j_{i-1}{g}_{k-i+1}$ , $j_{i-1}$ and $g_{k-i+1}$ are one-to-one correspondence, then $w_{j^{\prime }}=w_g=w_p=w_q$ .

We denote the digit of j' with $w_{j^{\prime }}$ , according to $r_i+r_{k-i+1}=j_{i-1}{g}_{k-i+1}$ , $j_{i-1}$ and $g_{k-i+1}$ are one-to-one correspondence, then $r_i+r_{k-i+1}$ .

We denote the digit of j with $w_{j^{\prime }}$ , then $w_j=w_{j^{\prime }}+1$ .

Finally, $p\oplus q=j+g$ , the vertical formula of addition is:

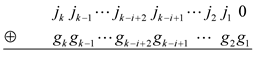
In the above formula, the rule of adding two numbers in the same position is the same as our usual addition.

For example: $\frac{\begin{array}{l}365\\ +563\end{array}}{\begin{array}{l}010\\ 828\end{array}}$ $\to$ $\frac{\begin{array}{l}365\\ +563\end{array}}{\begin{array}{l}0100\\ 828\end{array}}$ $\to$ $\frac{\begin{array}{l}0100\\ +828\end{array}}{928}$

$365+563=0100+828=928$ .

where 828 is the pure single digit g of sum and 0100 is the pure carry digit j of sum; where, p = 365, q = 563, g = 828, j' = 010, j = 0100.

$w_p=w_q=w_g=w_{j^{\prime }}=3$ , $w_j=4$ .

Next, we use theorem 1 and theorem 2 to characterize the properties of g and j.

Part 2

Theorem 1: As all the numbers in j are 0, j is a palindrome number; as the numbers in j are not all 0, j is a non-palindrome number.

Proof: As all the numbers in j are 0, whether there are 2m − 1 ( $m\in Z^{+}$) zeros or 2m ( $m\in Z^{+}$) zeros, always corresponds to 0, which has symmetry, so j is a palindrome number.

As the numbers in j are not all 0, we use the method of counter evidence to prove it.

Suppose that when the numbers in j are not all 0, j is the palindrome number. It is proved in two cases according to the parity of j' digits.

1) $w_{j^{\prime }}=2m-1$ ( $m\in Z^{+}$).

When the numbers in j are not all 0, it is equivalent that the numbers in j' are not all 0. Since j' is a symmetric number, it is advisable to set the symmetry center of $j^{\prime }=abc\cdots hikMkih\cdots cba$ , The center of symmetry of j' is M. Then $j=abc\cdots hikMkih\cdots cba0$ , the center of symmetry of j is the middle of M and k on the right side of M.

By the assumption that j is a palindrome number, we get M = k, k = i, i = h, …, c = b, b = a, a = 0.

So all the numbers in j are 0, that is, $M=k=i=h=\cdots =c=b=a=0$ .

This contradicts the hypothesis “the numbers in j are not all 0”.

Therefore, the proposition “As the numbers in j are not all 0, j is not a palindrome number” is correct.

2) $w_{j^{\prime }}=2m$ ( $m\in Z^{+}$).

When the numbers in j are not all 0, it is equivalent that the numbers in j' are not all 0. Since j' is a symmetric number, it is advisable to set the symmetry center of $j^{\prime }=abc\cdots hikMMkih\cdots cba$ , and the symmetry center of j' as the middle position between the two M. Then $j=abc\cdots hikMMkih\cdots cba0$ , and the center of symmetry of j is M on the right.

By assumption that j is a palindrome number, we get M = k, i = h, …, c = b, b = a, a = 0.

So all the numbers in j are 0, that is, $M=k=i=h=\cdots =c=b=a=0$ .

This contradicts the hypothesis “the numbers in j are not all 0”.

Therefore, the proposition “As the numbers in j are not all 0, j is not a palindrome number” is correct.

Therefore, as the numbers in j are not all 0, j is not a palindrome number.

Thus theorem 1 is correct.

Corollary 1: The center (middle most position) of any natural number is the symmetry point. As long as the sum of two numbers at the left and right symmetry positions is greater than or equal to 10 (as the number of digits of natural number is odd, the middle number is greater than or equal to 5), the sum obtained by adding the number and its inverted number must not be palindromes.

In other words, as a number is summed with its inverse number, once the carry is 1, it is known that its sum must not be a palindrome number.

Corollary 2: If the center (middle most position) of any natural number is the symmetry point, and the sum of the two numbers on the left and right symmetry positions is less than 10 (as the number of digits of the natural number is odd, the middle number is less than 5), then the sum obtained by adding the number and its inverted number must be palindromes.

Theorem 2: The sum of any palindrome number H and any non-palindrome number j must not be a palindrome number.

Prove: We denote the number of digits of H with $w_H$ .

1) As $w_H\equiv 1\left(\mathrm{mod}2\right)$ , let the palindrome number

$H=l_1{l}_2\cdots l_i{}_{-1}{l}_i{l}_{i+}{}_1\cdots l_{k-1}{l}_k{l}_{k-1}\cdots l_{i+}{}_1{l}_i{l}_i{}_{-1}\cdots l_2{l}_1$ ,

$j^{\prime }=j_1{j}_2\cdots j_i{}_{-1}{j}_i{j}_{i+}{}_1\cdots j_{k-1}{j}_k{j}_{k-1}\cdots j_{i+}{}_1{j}_i{j}_i{}_{-1}\cdots j_2{j}_1$ .

We denote the non-palindrome with j which being obtained after adding a 0 at the most end of j', then

$j=j_1{j}_2\cdots j_i{}_{-1}{j}_i{j}_{i+}{}_1\cdots j_{k-1}{j}_k{j}_{k-1}\cdots j_{i+}{}_1{j}_i{j}_{i-}{}_1\cdots j_2{j}_{1}0$ .

$\begin{array}{c}j+H=j_1{j}_2\cdots j_i{}_{-1}{j}_i{j}_{i+}{}_1\cdots j_{k-1}{j}_k{j}_{k-1}\cdots j_{i+}{}_1{j}_i{j}_{i-}{}_1\cdots j_2{j}_{1}0\\ +l_1{l}_2\cdots l_i{}_{-1}{l}_i{l}_{i+}{}_1\cdots l_{k-1}{l}_k{l}_{k-1}\cdots l_{i+}{}_1{l}_i{l}_i{}_{-1}\cdots l_2{l}_1.\end{array}$

Because j is a non-palindrome number, it contains at least two numbers 1. We might as well set j_i = 1, the rest number j₁, j₂, …, j_k−1, j_k are all 0. Then

$j=00\cdots 010\cdots 000\cdots 010\cdots 000$ .

$\begin{array}{c}j+H=00\cdots 010\cdots 000\cdots 010\cdots 000\\ +l_1{l}_2\cdots l_i{}_{-1}{l}_i{l}_{i+}{}_1\cdots l_{k-1}{l}_k{l}_{k-1}\cdots l_{i+}{}_1{l}_i{l}_i{}_{-1}\cdots l_2{l}_1.\end{array}$

If j + H is palindrome number, we get:

$1+r_{i-1}=0+r_{i-1},$

$1=0.$

This is clearly wrong.

Therefore, j + H must be a non-palindromic number.

2) As $w_H\equiv 0\left(\mathrm{mod}2\right)$ , let the palindrome number

$H=l_1{l}_2\cdots l_i{}_{-1}{l}_i{l}_{i+}{}_1\cdots l_{k-1}{l}_k{l}_k{l}_{k-1}\cdots l_{i+}{}_1{l}_i{l}_i{}_{-1}\cdots l_2{l}_1$ ,

$j^{\prime }=j_1{j}_2\cdots j_i{}_{-1}{j}_i{j}_{i+}{}_1\cdots j_{k-1}{j}_k{j}_k{j}_{k-1}\cdots j_{i+}{}_1{j}_i{j}_i{}_{-1}\cdots j_2{j}_1$ .

We denote the non-palindrome with j which being obtained after adding a 0 at the most end of j', then

$j=j_1{j}_2\cdots j_i{}_{-1}{j}_i{j}_{i+}{}_1\cdots j_{k-1}{j}_k{j}_k{j}_{k-1}\cdots j_{i+}{}_1{j}_i{j}_{i-}{}_1\cdots j_2{j}_{1}0$ .

$\begin{array}{c}j+H=j_1{j}_2\cdots j_i{}_{-1}{j}_i{j}_{i+}{}_1\cdots j_{k-1}{j}_k{j}_k{j}_{k-1}\cdots j_{i+}{}_1{j}_i{j}_{i-}{}_1\cdots j_2{j}_{1}0\\ +l_1{l}_2\cdots l_i{}_{-1}{l}_i{l}_{i+}{}_1\cdots l_{k-1}{l}_k{l}_k{l}_{k-1}\cdots l_{i+}{}_1{l}_i{l}_i{}_{-1}\cdots l_2{l}_1.\end{array}$

Because j is a non-palindrome number, it contains at least two numbers 1. We might as well set j_i = 1, the rest number j₁, j₂, …, j_k−1, j_k are all 0. Then

$j=00\cdots 010\cdots 0000\cdots 010\cdots 000$ .

$\begin{array}{c}j+H=00\cdots 010\cdots 0000\cdots 010\cdots 000\\ +l_1{l}_2\cdots l_i{}_{-1}{l}_i{l}_{i+}{}_1\cdots l_{k-1}{l}_k{l}_k{l}_{k-1}\cdots l_{i+}{}_1{l}_i{l}_i{}_{-1}\cdots l_2{l}_1.\end{array}$

If j + H is palindrome number, we get:

$1+r_{i-1}=0+r_{i-1},$

$1=0.$

This is clearly wrong.

Therefore, j+ H must be a non-palindromic number.

Therefore, Theorem 2 is correct.

Part 3

Aummative proof: The following proves that the palindrome number conjecture is not correct.

Proof: let $p=r_1{r}_2\cdots r_{k-1}{r}_k$ , $q=r_k{r}_{k-1}\cdots r_2{r}_1$ , then

$p+q=r_1{r}_2\cdots r_{k-1}{r}_k+r_k{r}_{k-1}\cdots r_2{r}_1$ .

We call the summation of a natural number and its inverse ordinal number “specified addition”.

If the palindrome number is not obtained after the specified addition operation for the first time, and the number of digits of sum is not increased; if the palindrome number is not obtained after the specified addition operation for the second time, and the number of digits of sum is not increased; if the palindrome number is not obtained after the specified addition operation for the third time, and the number of digits of sum is not increased.

According to 1 + 1 = 2, 2 + 2 = 4, 4 + 4 = 8, 8 + 8 = 16, if the palindrome number cannot be obtained after the fourth specified addition operation, the number of digits of the sum must be increased by one digit, that is, after no more than four consecutive specified addition operations, the number of digits of the sum obtained for the fourth time must be increased by one digit to become k + 1 digits. Therefore, as a number cannot obtain the palindrome number through multiple operations, w_j increases as w_g increases.

$g_1,g_2,\cdots ,g_{k-i+1},\cdots ,g_{k-1},g_k\in \left\{0,1,2,3,4,5,6,7,8,9\right\}$ , the greater w_j, $g_{k-i+1}+1\ne g_{k-i+1}+0$ ( $k\in Z^{+}$ , $i=1,2,\cdots ,k-1,k$) appears in the sum. In this way, the formula will increase, and the greater the possibility that j is a number not all 0.

According to theorem 1: As the numbers in j are not all 0, j is not a palindrome number, therefore, as a number cannot obtain the palindrome number after multiple (about 8 times) operations, w_j increases with the increase of w_p, w_q, w_g and $w_{j^{\prime }}$ .

According to theorem 2: The sum of any palindrome number and any non-palindrome number must not be a palindrome number. It can be seen that w_j gradually increases with the increase of operation times, and with the increase of w_j, the possibility of getting the palindrome number is getting smaller and smaller. When the number of digits becomes more, you may get a palindrome number occasionally. The probability of this situation is extremely small.

Therefore, the palindrome number conjecture is not correct.

196, 295, 394, 493, 592, 691, 790, 1495, 1585, 1675, 1765, 1855, 1945, 227386 are the counter examples.

Acknowledgements

I would like to express my deep appreciation to Professor Qiao Hu-sheng and Professor Yang Yong-bao of Northwest Normal University, Professor Qi Zhong-bin of Lanzhou Institute of Technology, Senior English Teacher Mr. Yin Zheng-Rong of Gansu province Long-xi County Education Bureau for their great help!

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Zheng, Z., Wang, S.H. and Zhang, Y.D. (2009) Based on the VC Palindrome Conjecture Inspection Algorithm. Computer Development & Applications, 22, 1-2.
[2]	Kong, L.D. and Jie, L. (2007) Natural Number 196 Palindrome Conjecture to Test the New Algorithm. Computer Engineering and Design, 28, 5841-5843+5853.
[3]	Guo, J.Z. and Yong, G. (2008) Program Selection Algorithms and Techniques. Mechanical Industry Press, Beijing, 100-101.
[4]	Zhang, W.Z. (2005) Mathematics and Mathematics Education from a Cultural Perspective. People’s Education Press, Beijing.
[5]	https://baike.so.com/doc/6344828-6558451.html.