1. “Three-Stage” Alternative Assessment
Over the last decade, innovative ways to assess achievement have become a topic occupying leader in education. Beginning in the 1980s, educators in various countries, including Israel, began examining methods used to assess students and concluded that, in effect, teaching was being adapted to the testing methods instead of vice versa ( Watt, 2005 ; Firestone, Winter, & Fitz, 2000 ).
Traditional assessment tests do not give sufficient information regarding the intrinsic abilities of the student. They emphasize factual information, and address procedures and skills without any depth or discussion. In addition, using only one method of assessment tends to skew the results in favor of one specific group of learners without giving a comprehensive picture regarding the abilities of others. To effectively test a wide range of learners necessitates a variety of documented methods for collecting evaluative information ( Watt, 2005 ). On the other hand, teaching that integrates assessment into the syllabus tends to be more open and sensitive to individual differences and can reflect any deeper, broader understanding that learners may have ( Birenbaum et al., 2006 ).
New trends worldwide emphasize the need for learners to develop the ability to solve problems, think critically, ask questions, make effective use of information, and more ( NCTM, 2000, 2004 ). Because standard assessment tools do not address these skills, there is a definite need for innovative student assessment tools.
This article presents a tool that is based on the “Three-Stage Assessment” tool introduced by a team of mathematicians at the Weizmann Institute of Science (details in “Methodology”) and that was adapted to assess pre-service and in-service primary-school mathematics teachers taking a course entitled “Geometry and Teaching Geometry” ( Ilany & Shmueli, 1999 ). The course focused on recognizing geometric shapes, their properties, and the relationships between them, along with general pedagogical aspects, and was given as a workshop that emphasized the use of appropriate illustrative material. The course also touched upon various teaching and didactic methods, and several studies and theories were discussed, including Van Hiele’s model regarding the stages in pupils’ geometric thinking. The course involved collaborative work in heterogeneous groups and class-wide (plenary) mathematical discussions, with an emphasis on solving authentic tasks that required research and discovery. Emphasis was placed on addressing typical errors made by pupils and the importance of using demonstrative techniques.
An effort was made to adapt student assessment to the teaching method. To this purpose, an assessment tool was designed that would test the mathematical and methodical knowledge of the students, both individually and as an expression of the processes of investigation they experienced within the group—taking into account student diversity.
The questions were adapted to the course content with the specific intent of addressing some of the problems and incorrect perceptions that often arise in geometry that have been described in the professional literature ( Rodriguez, 2008 ; Hershkowitz, 1989 ).
The purpose of this article is twofold: to introduce a tool that is particularly useful in the collaborative teaching setting, and to present the results of our study that examined the efficacy of this tool in assessing knowledge in this particular course and the impressions of the students.
Theoretical Background: The Rationale for Assessment Alternatives
Assessment is an integral component of the process of teaching-learning; in its absence, systematic learning cannot happen ( Black & Wiliam, 1998 ; Wiliam, 2011 ). In recent years, much attention in educational discourse has been given to alternative assessments that focus on the learning process and not just the final product. Introducing authentic tasks (situations from daily life) increases interest and intellectual challenge, provides reliable information on individual learning, and tests a variety of skills, especially those required for functioning in contemporary society. They provide an anti-thesis to predominant assessment methods that were found wanting, particularly by professionals ( Shepard, 2000 ; Nieminen, Chan, & Clarke, 2021 ).
The term “alternative assessment” may refer to any number of ways used to assess student achievement. To some, it means any form of assessment other than multiple-choice tests; to others, it means assessing performance using authentic tasks ( Birenbaum, 2014 ).
Traditional evaluation assessment may be considered to be a result of a “testing culture,” whereas alternative assessment might be considered “assessment culture” ( Birenbaum, 2014, 2015 ). The traditional approach to assessment is generally by means of an exam that is not always adjusted to the teaching method. Because the learning process is usually based on frontal lectures, the exam requires the learner to show that he has adequately memorized the material, and there is no real connection between the teaching that actually occurred in the classroom and the assessment. The role of the exam is merely to summarize knowledge, and the results provide feedback only after the learning process. The teacher creates the exam without any consideration of her learners’ day-to-day reality. The exam consists of questions that require precise answers, and there is usually only one correct response ( Anderson, 1998 ; Shepard, 2000 ).
In contrast, alternative assessment is based on integrating assessment into the teaching-learning process. For this reason, one may refer to it as “teaching-learning-assessment.” Teachers utilize the assessment to keep track of the learners’ thinking processes, thus improving teaching, which will now be more focused on providing in-depth understanding and letting learners actively take responsibility in their acquisition of knowledge. The assessment requires higher order thinking skills and not just rote memorization ( Birenbaum, 2014 ; Anderson, 1998 ).
Alternative Assessment in Teaching Mathematics
The Professional Standards for Teaching Mathematics reports ( NCTM, 2000, 2004 ) recommended instituting changes in mathematical education and reevaluating pedagogical concepts in preparation for the 21st century. Special importance was given to encouraging independent and critical thinking, and it was strongly recommended that math instruction should be changed from how many teachers had experienced it as students. Five key changes were suggested.
1) Making the classroom a “mathematical community” instead of a collection of individuals.
2) Encouraging students to rely on their own logic and mathematical evidence instead of on what the teachers say.
3) Allowing students to use their own judgement and mathematical reasoning instead of memorizing procedures.
4) Giving students the time to speculate and be inventive instead of demanding the “correct” answer only.
5) Linking the various topics and principles to the many mathematical applications instead of upholding the perception that mathematics is a collection of isolated concepts and skills.
The reports placed emphasis on thinking processes and problem-solving strategies rather than simple skills or technical aspects of mathematical concepts. In other words, they asserted that discussion and analysis during the processes of solving complex tasks are more important than merely checking the correctness of answers. This altered teaching will offer a variety of learning frameworks, including individual and collaborative work.
With this new approach, more tasks involving non-algorithmic solutions and higher-level thinking should be introduced into both teaching and assessment, including tasks that are somewhat unusual in nature, that do not necessarily have predetermined solution schema, and that require creative thinking to cope with finding a solution ( Schoenfeld, 1982 ). In addition, open questions can allow students to choose strategies appropriate to their cognitive levels, and unconventional and thought-provoking open questions allow students to investigate the problems in greater depth, make use of their originality, and assess their progress on their own.
Tasks such as those described above are termed “authentic.” Authentic tasks may originate from everyday experiences that can serve to instruct and assess ( Clarke & Sullivan, 1992 ) and are valuable in that they reflect problems that may be encountered in real life. Authentic tasks are often complex and not unequivocally defined, and their solutions may require several steps and may involve more than one correct answer. Completing the assignment requires judgment in choosing and applying appropriate knowledge, and skill in prioritizing and organizing the clarification stages and solution methods. It may be done by individual students in a natural situation without limitation of time, tools, and resources ( Falchikov, 2004 ).
Authentic tasks motivate students to persevere despite any difficulty in understanding the concepts because the value of the assignment extends beyond a mere demonstration of skills; they allow students to demonstrate comprehensive intelligence, thus making them more involved in a realistic goal. Such tasks often require students to collaborate without direct guidance by the teacher ( Chan & Clarke, 2017 ; Langer-Osuna et al., 2020 ; Langer-Osuna, 2018 ; Yeo, 2017 ). Students in classes stressing authentic achievement tend to be more involved in the learning process. Furthermore, authentic challenges nurture higher-order thinking and problem-solving skills, which will be useful to both the individual and society.
Changes such as these in the content and teaching of mathematics necessitate corresponding changes to the assessment process ( NCTM, 2000, 2004 ; MSEB, 1993 ). As a result, a variety of alternative and supplemental assessment methods and tools have been suggested to link between learning and teaching and the assessment process ( Stenmark, 1991 ), and focus on suitable evaluative assignments adapted to the teaching method. Such assessment should aspire to the following: to allow the student to present and explain his approach to solving the problem; to indicate whether the student is able to connect different mathematical areas; to demonstrate the significance of mathematics with respect to the real world; and to determine whether the student has obtained valuable knowledge.
Based on these requirements, we developed and studied an alternative assessment tool based on collaborative study groups and authentic tasks for use in a one-semester “Geometry and Teaching Geometry” course for pre-service teachers.
Urdan & Paris (1994) have stated that most teachers feel negative about standardized tests. Most believe that traditional tests do not reflect what students learn in school. Because of the emphasis placed on test scores, instruction is generally directed to ensure success in the test rather than learning for its own sake. Therefore, it was also important for us to receive feedback from the participants regarding our assessment tool and how it was adapted to the course.
Thus, the goals of the study were twofold: to study the effectiveness of the “Three-Stage Assessment” tool and to receive feedback from the participants regarding their impressions of the tool’s effectiveness and their intentions with respect to incorporating the tool into their teaching program. Based on our goals, we formulated three questions: a) How does this tool assess the participants’ mathematical and methodical knowledge of elementary-school geometry? b) How does this tool take into account cooperative work, personal knowledge, and diversity between the participants? c) What contribution to teaching do the participants believe this tool can make? The bulk of the data were the results of the “Three-Stage Assessment”; additional data was obtained from a feedback questionnaire, and from personal interviews.
2. Method
1While various teachers’ colleges include special tracks for teachers aiming to become primary school mathematics teachers, this particular college required all pre-service teachers (not only those aiming to teach mathematics) to take the “Geometry and Teaching Geometry” course.
The study population included 34 pre-service and in-service elementary school teachers in two classes of a one-semester course entitled “Geometry and Teaching Geometry in Elementary School” at Beit Berl Academic College, Faculty of Education (Class 1 had 16 participants, Class 2 had 18 participants). The groups were heterogeneous in that they included some teachers who were specializing in mathematics and some who were not.1
The course was presented as a one-semester workshop based on the Collaborative Learning approach ( Chiu, 2000 ). Assessment of student progress was made using the “Three-Stage Assessment” (developed by a Weizmann Institute team: Robinson, Buskila, Adin and Koren, in 2004), utilizing appropriate didactic and mathematical tasks to correspond to the topics covered in the course. A number of assignments were given throughout the course, and each was assessed in a three-stage process:
Stage 1: Group Assessment. Groups of three or four students were given a task aimed to demonstrate the participants’ command of some mathematical concept, their awareness of typical student errors regarding this concept, and their familiarity with various didactic means for teaching and illustrating the concept to pupils.
The students tackled the task as a group and became aware of the processes required for solving the assigned task, practiced expressing their ideas to others, and learned how to conduct effective mathematical discourse in a group setting. They submitted a single joint report, written without any teacher intervention, and reflecting the group’s strategies, including any erroneous ones. The group effort also allowed weaker students to learn from stronger ones (see Appendix 1a).
Stage 2: Class Discussion. The teacher reviewed the reports, summarized and consolidated the groups’ findings, and then conducted a 20-minute (approximately) class discussion, while also demonstrating an activity she had prepared that took into account any difficulties revealed by the group reports. This helped students summarize and generalize the concepts and develop a more comprehensive and deeper understanding of the mathematical and didactic principles involved. The discussion also gave the teacher an opportunity to form an impression of the individual knowledge of the group members, and to guide the discussion appropriately (see Appendix 1b).
Stage 3: Individual Assessment. Students were then tested individually (see Appendix 1c). The test questions, based on the stage-1 assignment and the stage-2 discussion, aimed to assess the student’s understanding of the tasks and principles involved. The test took about an hour and a half.
Besides giving an indication of the student’s knowledge regarding the subject matter, the individual assessment assessed what the student had learned from the group work and subsequent discussion. Students who were able to deepen their understanding on their own expressed this ability in their individual work.
A further advantage of this stage is that it motivated participants to become fully involved in the group activities, knowing that there would be a “final” test regarding the material.
Data Analysis of “Three-Stage Assessment”
To aid in qualitatively assessing the assignments (stages 1 and 3), rubrics were designed with specific, fully defined criteria levels for each question (see samples in Table 2). Each report was given a “general group score” (maximum 100). The final score for each student combined their group score (50%) and their individual score (50%). The final grade for the course was based on all the assignments given throughout the course. This paper evaluates one such assignment.
Feedback Questionnaire and Interviews. At the end of the course, participants filled out a 12-question questionnaire assessing their impressions of the course in general and the “Three-Stage Assessment” tool in particular. An open question allowed them to freely state their opinion regarding the tool and how they might integrate it into their work.
Interviews were conducted with a random sample of ten participants to validate the questionnaires.
3. Results (Part 1): “Three-Stage Assessments”
The overall results of the assessment for both classes were similar. For the purpose of this report, we detail two group reports (see sample in Appendix 1a) and two individual reports (one “satisfactory” and one “unsatisfactory” answer for each) from Class 1 (see Appendix 1c) and present the analyses of the questionnaires (from both classes) and the interviews.
Overall Grades
The grades for both the group reports and individual assessments for one of the assignments given to Class 1 (16 students) are presented in Table 1 along
![]()
Table 1. Scores (grading) of Class 1 (in percent).
with the final scores for each student. All the group scores were between 80 and 88, while individual scores ranged from 67 to 99. For three students, the individual scores were at least five points lower than the group scores, for seven, they were at least five points higher, and for six, they were similar. This is slightly different from the results of Class 2 (eight students higher, four students lower, six similar). In one extreme, a student in Class 2 received 52% on the individual test while the score for her group assignment was 90%, whereas another received 98% individually, yet the score of her group was only 63%. These cases will be discussed further on.
Sample of a Group Report Assessment (Sample Question)
The group assignment analyzed herein consisted of four questions (see Appendix 1a). Following are two sample group reports answering the second question, which had two parts: A. List some typical errors regarding the concept of the diagonal and its definition; B. Write questions to test your pupils’ knowledge, taking into account each one of the errors you listed. For each question, note which error it addresses and how.
The rubric shown in Table 2 scaled the following criteria from 0 to 5: list of errors, understanding the concept of the diagonal, sample questions, stating which error the questions test.
Samples of two group reports (one satisfactory and one unsatisfactory) and their assessments are shown below.
Group report, sample 1 (unsatisfactory)
![]()
Table 2. Rubric for group test, question 2.
Question 2
Part A: The diagonal (typical errors)
a. Connecting the line from one vertex to an adjacent one.
b. Connecting a line from a vertex to a vertex that is not adjacent but the line is not straight.
c. Not drawing all the possible diagonals.
d. Connecting two vertices with a broken line.
e. Connecting a vertex to the middle of a side.
Part B: Following are some illustrations of triangles and diagonals [sic]. For each one, note if the line is a diagonal or not.

(Note: Instructor’s comment: There are no explanations!)
Analysis of the answer based on rubric criteria.
Criteria 1: List of typical errors. It can be seen that the list of typical errors is incomplete and lacks explanation. Although five “errors” are listed, they are not all “typical” errors. For example, c, “Does not draw all the possible diagonals” is not a relevant answer. Furthermore, some common errors are missing, such as drawing the diagonal outside the polygon or drawing a diagonal that is partly within and partly outside the polygon.
Criteria No. 2: Understanding the concept of the diagonal. The answer shows that the students do not have a clear understanding of the concept of diagonal: a) Three out of four examples illustrate “diagonals” within a triangle, when triangles do not have diagonals; b) There are no explanations to show understanding.
Criterion No. 3: Sample questions. The students gave only one sample question, inappropriately phrased (stating that the illustrations have “diagonals”) and using insufficient examples that will not properly test their pupils’ understanding of the concept of “diagonal.”
Criterion No. 4: Stating which error the questions test. There is no indication next to any of the examples regarding which error it tests and how.
Conclusions: This sample indicates that the group of students are not aware of all the problems that pupils may have in the given topic. They listed only a few actual errors and showed no understanding of the source of these errors. They show no mastery of the topic, neither mathematically nor didactically.
Group report, sample 2 (satisfactory)
Question 2
Part A
a. The pupil thinks that the diagonal must always be inside and cannot be outside the polygon (shape c and d test this idea).
b. The pupil knows where the diagonal originates but does not know where it is supposed to go (shape d).
c. The pupil draws the diagonal in the shape of an arc (shape d).
d. The pupil draws only one diagonal for a shape and ignores any others (shapes d and e).
e. The pupil begins the diagonal from the corner and ends it on a side (all the shapes). For example: 
f. The student states that the side is also a diagonal.
Part B: Draw the diagonals, beginning at the dots.

Analysis of the answer based on rubric criteria.
Criteria 1: List of typical errors. A complete list of typical errors was given, with illustrations that explain their intent. However, it is not clear how each illustration illustrates the error. For example, they state that shape “d” tests statement 1b, “The pupil knows where the diagonal originates but does not know where it is supposed to go,” but they do not state how.
Criteria No. 2: Understanding the concept of the diagonal. The answer clearly indicates that the students understand the concept of diagonal.
Criterion No. 3: Sample questions. The students wrote only one question, however it gives excellent examples for testing pupils’ knowledge regarding the concept of the diagonal.
Criterion No. 4: Stating which error the questions test. They noted in each example which error it checks and how.
Conclusions: From the example, it can be seen that the students understand difficulties that may arise in understanding this topic and are aware of typical errors, including the source of the misunderstandings and now how to address them. They have mastered this topic both mathematically and didactically.
Sample of an assessment of an individual test (Sample Question)
The individual test included three questions. We present an analysis of the first question based on the rubric shown in Table 3:
Question 1
1) Suggest an appropriate activity for the topic “triangles” that does not use
![]()
Table 3. Rubric for individual test, question 1.
straws, pipe cleaners, or a worksheet. Explain your didactic reasons for each stage of the activity, the goal of the activity, what it is checking, etc.
2) Give two names for the triangle below.
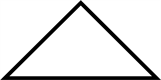
3) Which of the two names do you think most of the class would use, and why?
Following are two examples of answers to this question and their assessment.
Individual test, sample 1 (unsatisfactory grade)
Question 1
Planning Activity:
Topic: Names of triangles (sorting triangles)
Grade: 4
Van Hiele Level: 2
Goal of the Activity: Sorting triangles (each type of triangle and its name)
Previous knowledge required: angles, triangle
Materials: Worksheets and pictures of triangles.
Description of the activity: Give each pupil various drawings of triangles. Ask them to sort the triangles according to common properties.
After sorting the triangles, the child should conclude that there are three types of triangles: acute triangles, right-angle triangles, and obtuse triangles.
Didactic considerations:
1) The child knows how to measure angles.
2) The child knows the names of the angles (types of angles and how many degrees they are):
Acute angle < 90 (less than 90)
Right angle = 90
Obtuse angle > 90 (more than 90)
Questions for discussion with pupils to summarize activity:
1) What are the properties of acute triangles, right-angle triangles, and obtuse triangles?
2) What is the difference between each triangle?
Another example of an activity:
In this activity, the children use a geoboard and elastic bands.
Instruction page:
1) Using the geoboard and elastics:
a. Make any triangle on the geoboard. Check the three angles using the corner of a rectangle.
b. Circle the correct name of the triangle according to its angles:
Right-angle Obtuse Acute
2) a. On the geoboard, construct an obtuse triangle and draw it.
b. Construct another obtuse triangle that is different from the first one and draw it.

3) a. On the geoboard, construct a right-angled triangle and draw it.
b. Construct other right-angled triangles that are different from each other, and draw them.

4) a. On the geoboard, construct an acute triangle and draw it.
b. Construct another acute triangle that is different from the first one and draw it.
Enjoy your work!
Another activity with triangles: You can use matchsticks to build different triangles.
Analysis of the answer based on rubric criteria.
Criterion 1: Understands Concepts: Uses mathematical concepts relevant to the activity. (The student states a concept and shows that he understands it.) The student shows the appropriate use and understanding of the mathematical concepts.
Criterion 2: Appropriate Use of Model (for demonstration). Even though the instructions stated that worksheets should not be used, the student prepared an activity using worksheets. However, she also prepared other activities using a geoboard. The worksheet does not make use of the model (she wrote: “Give each child different drawings of triangles,” but she did not illustrate them).
Criterion 3: Clear Explanation of Activity. The activities on the worksheet are not clearly described. Nevertheless, the activities using the geoboard are well-detailed, although they seem to have been developed spontaneously, and there is no indication of defining the goals or what each stage of the activity is meant to attain.
Criterion 4: Presentation of Task. The worksheet clearly does not give details of the activity. Nevertheless, the activity using the geoboard is clearly presented, though it is not clear what the connection is between all the parts of the activity and its ultimate goal.
Criterion 5: Didactic Considerations. The worksheet indicates that the student is confusing didactic considerations and previous knowledge. In addition, no didactic considerations are indicated regarding use of the geoboard.
Criterion 6: Consideration of Activity’s Goals. The worksheet details the goal of the activity. However, goals are not defined with the geoboard activity nor does the student say what each of the questions in the activity checks and how.
Conclusions: The student has made use of demonstrative techniques, but it is on an average level and does not exhibit knowledge regarding the advantages and disadvantages of the various techniques. The goals of the activities are not sufficiently detailed, and although the instructions are clearly stated, there is no indication where the activity is meant to lead or of didactic considerations.
Individual test, question 1 (satisfactory grade)
Question 1: Activity with Triangles
Goal: a) The student will understand the concept of “height”
b) The student will understand the concept of heights in congruent triangles.
Equipment: Large triangles from stiff material
Strings
Beads
Readiness: The student must understand the concept of “vertical line.”
Stages of the Activity
A. 1) The pupils receive triangles that have already been prepared with strings and beads. Each group receives three triangles: right angled, obtuse, and acute.
2) The pupils are asked to form line segments that are vertical to the sides that are equal in the triangles using the strings and the beads.
B. The pupil must investigate:
1) How many vertical lines are there in each triangle?
2) How many vertical lines are there for each side?
3) Must the vertical lines pass through the triangle?
4) How many vertical lines pass through the triangle?
5) Is there a connection between the type of angles in the triangle and the vertical lines that pass through the triangle?
C. Explain to the pupils that the vertical lines that they discovered are “heights.” The pupils must describe “height.”
Analysis of the answer based on rubric criteria:
Criterion 1: Understands Concepts: Uses mathematical concepts relevant to the activity. (The student states a concept and shows that he understands it.) The student showed that she understood the concept correctly.
Criterion 2: Appropriate Use of Model (for demonstration). The student used the demonstration means appropriately.
Criterion 3: Clear Explanation of Activity. The activity is well-detailed and clear.
Criterion 4: Presentation of Task. The presentation is clear, detailed, and properly ordered.
Criterion 5: Didactic considerations. No didactic considerations are specified.
Criterion 6: Consideration of Activity’s Goals. Two goals are specified, but the activity only relates to the second of them (that is to say, there is only partial consideration of the goals).
Conclusions: The student correctly used demonstration techniques. She was able to construct different, varied activities for the pupils that include exploration and discovery, and she properly used relevant means of demonstration.
It appears that she has mastered the relevant mathematical concepts for the activity, takes into consideration any difficulties her pupils may encounter, is aware of typical errors and their sources, and knows how to address them (although she doesn’t address all the difficulties that may arise regarding the topic of “height,” and relates more to the specific problems that may arise during the activity she has designed).
The goals of the activity are detailed and the activity is presented clearly, but it does not address all the goals of the activity.
4. Results (Part 2): Student Feedback and Interviews
A Likert-type questionnaire (scale: 1 - 5) with 12 statements regarding the use of the tool and its incorporation into mathematics teaching was distributed to all the participants at the end of the course.
The results are presented in Table 4. These results, along with the interviews, indicate that the tool was agreeably received. It is apparent that the participants felt that the group activity (Stage 1) contributed to their individual knowledge and their success in the individual test. “The group activity was good. We discussed the problems together, divided up the roles ad hoc, and helped each other. Everyone came up with questions, which forced the others to help out and answer.” Another respondent: “During the group activity, we conducted a mathematical discourse where everyone remembered something else and contributed
![]()
Table 4. Summary of feedback regarding the “Three-Stage Assessment” tool.
and corrected. Everyone contributed another point of view.” The participants preferred working in groups and preferred being tested with the “Three-Stage” test rather than a conventional test. It was also apparent that the class discussion (Stage 2) was an important part of the process and contributed to the participants’ individual knowledge. The participants indicated that they would likely use such an assessment method for their pupils.
5. Discussion
The results of this study indicate that the “Three-Stage Assessment” tool provides an appropriate means of assessment for courses whose means of instruction, based on new trends in teaching, are primarily through corroborative work.
Following are the conclusions regarding the specific research queries.
Assessment of the Participants’ Mathematical and Methodical Knowledge of Elementary-school Geometry
The data indicate that the tool reflects the students’ knowledge to a large extent and accurately reflected their understanding of mathematical concepts, methodical knowledge (such as the ability to prepare activities for pupils), and the purpose of the assignment; their originality and creativity; and their ability to organize and properly communicate lessons and assignments. It was apparent that students were fully cooperative working on the group report, conducted meaningful discussions, offered conjectures, and mutually supported each other during the learning experience.
Regarding students who scored lower individually, the gaps between the two scores were explained upon examination of other tasks assigned during the course (not related to this study), and the impression formed by the teacher in the classroom made it clear that a lower individual score reflected the actual knowledge of the student. In fact, these students did not exhibit competence with the material studied during the lessons, and the difference in the scores is a result of their participation in a group with students who had mastered the material. This is especially apparent in one extreme case of a student who received 52% on the individual test while the score of the group test was 90%.
When working in groups, students at all levels worked together, supporting and inspiring each other, and the concerted effort naturally produced a group report that was high in quality and reflected the knowledge and greater input of the more proficient students. Thus, it may be presumed that students whose individual scores were subsequently higher than the group score had successfully learned from the group discussion and extra assignments. This conjecture was supported through the subsequent interviews, in which students said they had learned from the group test.
Regarding the student who received 52% on the individual test while the score of the group test was 90%, familiarity with this student and her work showed that she, too, had not mastered the material. The group, however, included students who had mastered the material well, and it may be assumed that they dominated the results of the group test leading to this gap between the scores.
An interesting case is that of a student who scored 98% on the individual test while her group scored only 63% (Class 2). Further testing indicated that two of the students in that group did not show mastery over the material, and while it would seem that the stronger student should have “given the correct answers” for the group assignment, the interview with her indicated that she lacked self-confidence regarding her abilities and apparently had allowed the others in the group to “overrule” her input.
Assessment of Cooperative Work, Personal Knowledge, and Diversity Between Participants
The feedback indicated that the group work allowed students to overcome their diversity in skills when coping with the assignment. “When I work alone, I may get stuck on a particular idea, and don’t know if it’s correct. Working in a group, I discover additional approaches. For one question, my thinking was completely wrong, and the group corrected me.”
“Had I been working on my own, I would have needed the help of the teacher, but here, I did not have to depend on her.”
The individual test reflected and balanced the results of the group test. Information was provided regarding the knowledge of the different students based on their level and what they had learned in the group work and following the class discussion with the teacher. It can be seen that some students expanded their knowledge of the subject matter on their own, discovering their abilities during the individual assignment.
The individual test also pointed out the difference in knowledge between pre-service and in-service teachers. For example, when asked to give two names for a right-angled isosceles triangle, some pre-service teachers erroneously answered “acute triangle” and/or “equilateral triangle” which are typical errors made by pupils. Similarly, when the students were asked to list typical student errors regarding the concept of “diagonals,” only in-service teachers connected their answers to the Van Hiele levels.
Tool’s Potential Contribution to Teaching
The participants raised several key points that the “Three-Stage Assessment” addressed. They noted that the mathematical discourse in the groups and during the class discussion contributed to their mathematical and methodical knowledge. They asserted that working in groups helps develop cooperation skills and supportiveness (even beyond the mathematical aspect) and indicated that they preferred working in groups rather than individually because “it is much more interesting and productive.” The participants pointed out that they all worked diligently and cooperatively, felt engaged in the mathematical discourse, and that the preparation of the group report felt like a regular lesson and not a test. They enjoyed the activity; one of the students said: “It was really fun to do the test in the group even though I’m sure I didn’t get a hundred, but I didn’t mind because I learned a lot and enjoyed it.” This is not often heard regarding conventional tests. The interviews also indicated several other advantages to the group assignment such as reducing examination anxiety and creating motivation for cooperativity.
The techniques demonstrated by the teacher during the discussion helped them understand the material and provided a model of how to explain the material to their pupils in school.
New assessment method based on innovative teaching method. During the course, the students raised concern over how they would be evaluated in light of the new trends. The question that was repeated was “will the exam be a group exam because we are working in groups?” Following their experience with the “Three-Stage” tool, the participants stated that this method of assessment was indeed appropriate for the way that the course was conducted. For example, “When I began the course I didn’t understand how it would be possible to offer a group test. Now I see how it is possible to design a test that is appropriate for working in groups.”
This assessment method gave students an example of how to adapt the assessment method to the teaching method and to forego conventional test methods common in schools, where assessment is only quantitative in nature and the qualitative aspect does not come into account (a discussion about this was conducted in class). The results of this study indicate that the students are interested in using this tool to assess their pupils.
Overall, the participants seemed to feel that this tool was appropriate for the course and fulfilled its purpose. “During the individual test I was already feeling much better than I had in the group test, I was confident regarding the material, and there were concepts that I remembered from the group assignment and from the discussion.”
6. Conclusion
The implications of this study are that the “Three-Stage Assessment” tool, properly adapted, can be considered an “all-purpose” tool appropriate to any course that uses a more modern approach to teaching and assessment. It is uniquely appropriate for collaborative learning because it reflects the knowledge, originality, creativity, and skills of the learners while taking into account their diversity and the different ways they have of coping with group work and mathematical discourse. This tool would be excellently used as an additional assessment tool in many areas of mathematics. In addition, using this tool, as we did, in a teacher-training course stimulates discussion about the tool itself, which is important, as it introduces the topic of assessment into the class. The tool is flexible; it can be adapted to the teaching method, and the teaching method can be adapted to the tool.
Appendix 1: “Three-Stage Assessment” Tool
Appendix 1a. Group Assessment
Names:
Question 1
Two teachers meet in the teachers’ room. One has some straws and pipe cleaners and the other has a worksheet.
Teacher A: I can see that we are both teaching about triangles.
Teacher B: Yes. I have here a worksheet on the topic.
Teacher A: I prefer using straws and pipe cleaners.
1) Suggest some activities that are appropriate for the topic of “Triangles” using straws and pipe cleaners. (Write down the details of each of the stages of the activity, the goal of the activity, what it comes to test, etc.)
2) Look at the worksheet. Make suggestions regarding the activity and compare using straws and a worksheet. What are the advantages and disadvantages of each? Give your reasons.
Worksheet
Question 2
1) List some typical errors regarding the concept of the diagonal and its definition.
2) Write questions aimed to check pupils’ knowledge regarding each one of the errors you have listed. For each question, note which error it addresses and how.
Question 3
On the first square (on the left), an area is defined. Calculate the area of each of the shapes drawn in the other squares.
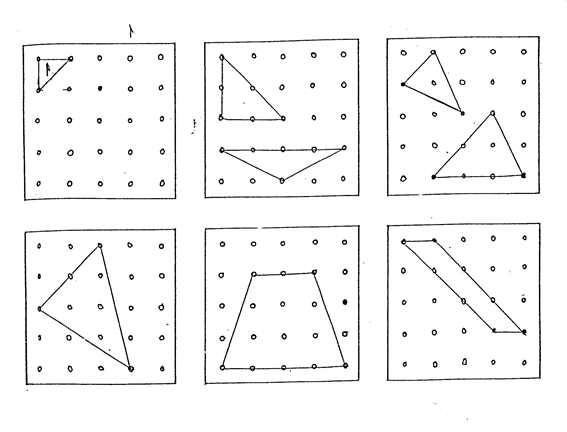
Question 4
A. This is a “one-year” square. 
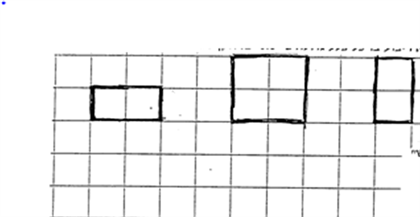
A “two-year” square is a square in which each side is twice as long. Circle the appropriate square.
Draw a “three-year square.
How many “one-year” squares are required to build a “three-year” square? ___ “n-year”? ___
How “old” is the square built from 49 “one-year” squares? ____
What is the relationship between these activities and the area of polygons on a plane?
A. This is a “one-year” cube.
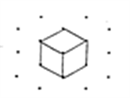
Circle the “two-year” cube? How many “one-year” cubes are needed to build it?
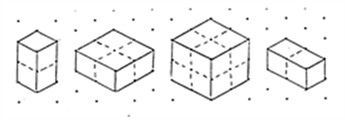
How many “one-year” cubes are needed to build a “five-year” cube? ___ “7-year” cube? ____ “n-year” cube? ____.
How many “two-year” cubes are required to build a “6-year” cube?
Draw a “three-year” cube.
![]()
Appendix 1b. Connecting Activity
We used the following two points as a basis for the discussion.
1) The advantages and disadvantages of using straws.
2) Various ways of calculating area on a geoboard.
These were chosen as representative activities that summarize the main points of the topics that the students dealt with in the group assignments. Discussing the pros and cons of worksheets and “straws” is very important didactically, and the second question on area was important because of the difficulties the students exhibited in this area.
Appendix 1c. Individual Assessment
Name:
Question 1
1) Suggest an appropriate activity for the topic of “triangles” that does not use straws, pipe cleaners, or a worksheet. Explain your didactic reasons for each stage of the activity, the goal of the activity, what it is checking, etc.
2) Give two names for the triangle below.
![]()
3) Which of the two names was given by most of the class and why?
Question 2
Create a page with examples and non-examples of diagonals. Present at least 5 of each (specify which are which). Explain.
Question 3
Square number 1 defines a unit of area. Calculate the area of each of the shapes below.