Necessary and Sufficient Conditions for the Separability and the R-Separability of the Irrotational Stokes Equation and Applications

Eleftherios Protopapas¹, Maria Hadjinicolaou²

¹School of Applied Mathematical and Physical Sciences, National Technical University of Athens, Athens, Greece.
²Applied Mathematics Laboratory, School of Science and Technology, Hellenic Open University, Patras, Greece.

DOI: 10.4236/jamp.2020.811176                

Abstract

In the present manuscript, we formulate and prove rigorously, necessary and sufficient conditions for all kinds of separation of variables that a solution of the irrotational Stokes equation may exhibit, in any orthogonal axisymmetric system, namely: simple separation and R-separation. These conditions may serve as a road map for obtaining the corresponding solution space of the irrotational Stokes equation, in any orthogonal axisymmetric coordinate system. Additionally, we investigate how the inversion of the coordinate system, with respect to a sphere, affects the type of separation. Specifically, we prove that if the irrotational Stokes equation separates variables in an axisymmetric coordinate system, then it R-separates variables in the corresponding inverted coordinate system. This is a quite useful outcome since it allows the derivation of solutions for a problem, from the knowledge of the solution of the same problem in the inverted geometry and vice-versa. Furthermore, as an illustration, we derive the eigenfunctions of the irrotational Stokes equation governing the flow past oblate spheroid particles and inverted oblate spheroidal particles.

Keywords

Axisymmetric Flow, Stokes Operator, Analytical Solution, Separation and R-Separation of Variables, Axisymmetric Orthogonal Coordinate Systems

1. Introduction

The flow of a Newtonian fluid, where the viscous forces dominate over the inertial ones is called Stokes flow [1]. Assuming the velocity field $v\left(r\right)$ and the pressure field $P\left(r\right)$, it is mathematically described through the system of equations $\mu \Delta v\left(r\right)=\nabla P\left(r\right)$, $\nabla \cdot v\left(r\right)=0$, $r\in \Omega$, where $\Omega \subseteq {ℝ}^3$ is the fluid domain, $r$ is the position vector and $\mu$ is the shear viscosity. This system of equations has been firstly used in spherical geometry for solving the flow: of the translation of a sphere [2], of two spheres in a viscous fluid [3], past a porous sphere with Brinkman’s model [4], inside a porous spherical shell [5], around spherical particles moving along a line perpendicular to a plane wall [6], past a sphere with slip-stick boundary conditions [7], of a rising bubble near a free surface [8], in a plane microchannel in the case that both walls have super hydrophobic surfaces [9] etc.

The assumption of axisymmetric Stokes flow has been usually employed for modeling engineering, physical and medical problems, such as filtration, fluidization, crystallization, hydrodynamic chromatography, transport phenomena, flow through membranes, flow of emulsions, colloids, suspensions of living cells, etc. employing models of either one or more particles in different arrangements. Axis symmetry is a well justified assumption when the fluid flows symmetrically around objects through channels and conduits. In general, these particles may be considered as bodies of revolution (being generated by rotation of a symmetrical surface along its axis of symmetry), e.g. sphere, prolate and oblate spheroids. In this way, 3-D problems turn out to depend only on two variables, let’s say: radial and azimuthal, while exhibiting polar angle independence (invariance under rotations). Consequently, the governing partial differential equation describes variations of physical quantities of only two independent variables.

Axisymmetric Stokes flow has been used to model: flow through porous media [2] [10], swarm of particles [6] [11] [12] [13], flow around a fluid prolate spheroid [14], flow around rotating objects [15], flow of microswimmers [16], flow inside a cylindrical container [17], flow of biological fluids like blood plasma [18] [19] or the relative flow of low density lipoproteins in blood plasma [20] [21]. When treating such problems, we are able to describe the flow field and the other quantities of interest: velocity, drag force, pressure, etc., through a scalar function, namely the stream function $\psi$, which satisfies the fourth order elliptic partial differential equation (PDE) $E^4\psi =0$ where $E^4=E^2\circ E^2=E^2\left(E^2\right)$ is the (rotational) Stokes operator and $E^2$ is the irrotational Stokes operator [2]. The stream function is obtained analytically using PDE techniques. Historical and technical information for the derivation of the analytical solutions can be found in [2] [22] and references therewith.

Analytical solutions provide the most accurate description of these hydrodynamic quantities at every point of the fundamental domain, without the computational effort a numerical approach would need. Despite the profound benefits of obtaining an analytical solution these are feasible only in few cases, when the translation of the equation in the assumed geometry allows for a separable form of the solution. It is utilized to any number of dimensions and becomes of significant importance when solving physical, biomedical or engineering problems, since the analytical form of the solutions of the associate Boundary Value Problems (BVPs) provide information for the physical characteristics of the problem and may shed to light limitations imposed by the model. The formulation of a well posed BVP requires the appropriate set of boundary conditions. For obtaining separable solutions, it is necessary to adopt a particular curvilinear coordinate system such that the boundary of the problem coincides to the one of the coordinate surfaces. In the case that the curvilinear coordinate system is an orthogonal one, the coordinate surfaces are orthogonal to each other. The separation of variables of a PDE is possible only if the coordinate surfaces are orthogonal, which unlikely it is not always achievable.

Attempts for obtaining analytical solutions of Stokes flow $E^4\psi =0$ are dating back to 19^th century, aiming to serve mostly engineering needs. Oberbeck [23] in 1876 derived a solution for Stokes flow caused by the steady translation of an ellipsoid in an unbounded fluid using Cartesian coordinates, while in 1891 Sampson [24] used spheroidal coordinates to obtain a partial solution of the Stokes flow around a translating spheroid along its main axis in an unbounded fluid. Payne and Pell in 1960 [25] derived a solution for Stokes flow around a spheroid. The analytical solution of the equation $E^4\psi =0$ in spherical coordinates is known for almost 170 years [2], but only 25 years ago, closed form solutions of Stokes equations were obtained in other than the spherical coordinate systems, namely the prolate and the oblate spheroidal ones. Precisely, Dassios et al. [11] managed to derive the complete solution of Stokes equations introducing for the first time the concept of semiseparation of variables. This delay may be due to the fact that in many engineering applications, the solutions in spherical geometry seem to be adequate for solving a problem. Semiseparation of variables is a kind of separation where particular combinations of products of functions of one variable are solutions while each component of the product is not. For an extensive review of the relative literature one may see [11]. Since then the semiseparation method has been used by many authors in many different problems. Zlatanovski [26] used the semiseparable solutions and the Brinkman’s model to study the flow past a porous prolate spheroidal particle, while Deo and Datta [14] solved the flow past a fluid prolate parallel to its axis of revolution. Moreover, Hadjinicolaou and Protopapas have shown that Stokes equation in the inverted prolate and oblate spheroidal systems of coordinates R-semiseparates variables [27] [28] [29].

The analytical solution of the irrotational Stokes flow $E^2\psi =0$ is also derived in each one of the aforementioned coordinate systems [2] [11] [27] [28] [29]. Furthermore, Deo and Tiwari in 2008 [30] derived the complete solution of the irrotational flow in R-separable form in bispherical and toroidal coordinate systems, while Protopapas [31] proved that Stokes operator separates variables in the parabolic coordinate system and it R-separates variables in the cardiod and the tangent sphere coordinate systems deriving the corresponding eigenfunctions.

Regarding mathematical rigor, Moon and Spencer in [32] and Morse and Feshbach in [33] presented a systematic way of deriving the necessary and sufficient conditions for the separation and the R-separation of the Laplace and the Helmholtz equations, in several coordinate systems. Although solutions and theoretical investigation for the Laplace and the Helmholtz equations in various orthogonal coordinate systems have been studied exhaustively, very few have been proved for the Stokes stream equation $E^2\psi =0$ and Stokes bistream equation $E^4\psi =0$, that govern the axisymmetric irrotational and the rotational creeping flow of an incompressible fluid.

In the present manuscript, we expand the existing theory for the separability criteria of the Laplace and Helmholtz operator to another elliptic operator, the Stokes one, $E^2$. Particularly, we investigate, formulate and derive the necessary and sufficient conditions for the separation or the R-separation of equation $E^2\psi =0$ in any axisymmetric coordinate system. The obtained results can serve as a criterion for determining whether irrotational Stokes equation $E^2\psi =0$ can accept a solution in separable or R-separable form, and thus assistance to attain it. In the case of R-separability, the exact form of the function R is also defined as part of the process. Taking into account that the solution of $E^4\psi =0$ is obtained through the use of the kernel space of $E^2\psi =0$, these necessary and sufficient conditions, may serve as a tool for deriving the analytical solution of the irrotational Stokes equation $E^4\psi =0$ in every axisymmetric coordinate system.

In the present study, we also reveal the interrelation of the type of separation of a solution in a coordinate system and the type of separation of the solution in the inverted one. Particularly, we prove that if the irrotational Stokes equation separates variables in one system, then it R-separates variables in the inverted one, while if it R-separates variables, it can also R-separates variables in the corresponding inverted system of coordinates. This is quite useful result since if analytical solution in any axisymmetric coordinate system is derived, then solution in the corresponding inverted one can be calculated without solving analytically the equation, by employing radial transformation.

The structure of this manuscript is as follows: In section 2 we provide the relevant mathematical background. In section 3 we present and prove our theoretical results for the necessary and sufficient conditions for the simple or the R-separability of Stokes equation and we derive the connection of the metric coefficients in any axisymmetric system and its inverted one. In section 4 we apply analytically the obtained results in the oblate, in the inverted oblate coordinate systems and briefly in other axisymmetric systems of coordinates, while all the outcomes are organized in tables, for convenience. To this end, we discuss the findings and present some final remarks.

2. Mathematical Background

We consider a Riemannian n-space with an orthogonal coordinate system where any point is defined by the variables $\left(u^1\mathrm{,}{u}^2\mathrm{,}\cdots \mathrm{,}{u}^n\right)$.

Definition 1. If the assumption

$u={\displaystyle \underset{i=1}{\overset{n}{\prod }}}{U}^i\left(u^i\right)$ (1)

allows the separation of the partial differential equation into n ordinary differential equations, the equation is said to be simply separable.

Definition 2. If the assumption

$u=\frac{1}{R\left(u^1,u^2,\cdots ,u^n\right)}{\displaystyle \underset{i=1}{\overset{n}{\prod }}}{U}^i\left(u^i\right)$ (2)

allows the separation of the partial differential equation into n ordinary differential equations, and R is a function of at least two variables which cannot be written as a product of one variable functions, the equation is said to be R-separable.

An axisymmetric system of coordinates $\left(q_1\mathrm{,}{q}_2\mathrm{,}\phi \right)\mathrm{,}\phi \in \left[\mathrm{0,2}\pi \right)$ is related to the Cartesian one $\left(x_1\mathrm{,}{x}_2\mathrm{,}{x}_3\right)$ with

$\left(x_1,x_2,x_3\right)=\left(\rho \left(q_1,q_2\right)\cos \left(\phi \right),\rho \left(q_1,q_2\right)\sin \left(\phi \right),z\left(q_1,q_2\right)\right).$ (3)

The scaling factors or the metric coefficients needed for describing the lengths of the basis vectors in the new orthogonal system are

$h_1=\frac{1}{\sqrt{{\left(\frac{\partial \rho }{\partial q_1}\right)}^2+{\left(\frac{\partial z}{\partial q_1}\right)}^2}},$ (4)

$h_2=\frac{1}{\sqrt{{\left(\frac{\partial \rho }{\partial q_2}\right)}^2+{\left(\frac{\partial z}{\partial q_2}\right)}^2}}$ (5)

and the radial cylindrical coordinate is

$\varpi =\left|\rho \left(q_1\mathrm{,}{q}_2\right)\right|\mathrm{.}$ (6)

The operator $E^2$ in the axisymmetric system of coordinates $\left(q_1\mathrm{,}{q}_2\mathrm{,}\phi \right)$ has the form

$E^2=h_1{h}_2\varpi \left[\frac{\partial }{\partial q_1}\left(\frac{h_1}{h_2\varpi }\frac{\partial }{\partial q_1}\right)+\frac{\partial }{\partial q_2}\left(\frac{h_2}{h_1\varpi }\frac{\partial }{\partial q_2}\right)\right].$ (7)

Assuming a function $\psi =\psi \left(q_1\mathrm{,}{q}_2\right)$, this satisfies the irrotational Stokes equation $E^2\psi =0$, which can be written as

$\frac{\partial }{\partial q_1}\left(\frac{h_1}{h_2\varpi }\frac{\partial \psi }{\partial q_1}\right)+\frac{\partial }{\partial q_2}\left(\frac{h_2}{h_1\varpi }\frac{\partial \psi }{\partial q_2}\right)=0.$ (8)

3. Theoretical Results

3.1. Simple Separability of the Irrotational Stokes Equation

In this section, we investigate the restrictions posed on the metric coefficients $h_1\mathrm{,}{h}_2\mathrm{,}\varpi$ of an axisymmetric coordinate system, under which the irrotational Stokes stream Equation (8) admits simple separable solution.

Theorem 1. Let $\left(q_1\mathrm{,}{q}_2\mathrm{,}\phi \right)$ an axisymmetric system of coordinates with metric coefficients $h_1\mathrm{,}{h}_2$ and radial cylindrical coordinate $\varpi$ . The equation $E^2\psi =0$ separates variables if and only if there exist functions $f_1\left(q_1\right)$ , $f_2\left(q_2\right)$ , $F_1\left(q_1\right)$ , $F_2\left(q_2\right)$ such that

$\frac{h_1}{h_2\varpi }=f_1{f}_2$ (9)

and

$\frac{h_2}{h_1\varpi }=F_1{F}_2.$ (10)

Proof. We assume that the function $\psi$ can be written in the form

$\psi \left(q_1\mathrm{,}{q}_2\right)=Q_1\left(q_1\right)Q_2\left(q_2\right)\mathrm{.}$ (11)

Substituting (11) into (8) we get

$Q_2\frac{\partial }{\partial q_1}\left(\frac{h_1}{h_2\varpi }\frac{\text{d}{Q}_1}{\text{d}{q}_1}\right)+Q_1\frac{\partial }{\partial q_2}\left(\frac{h_2}{h_1\varpi }\frac{\text{d}{Q}_2}{\text{d}{q}_2}\right)=0$ (12)

or equivalently

${Q^{″}}_1{Q}_2\frac{h_1}{h_2\varpi }+{Q^{\prime }}_1{Q}_2\frac{\partial }{\partial q_1}\left(\frac{h_1}{h_2\varpi }\right)+Q_1{Q^{″}}_2\frac{h_2}{h_1\varpi }+Q_1{Q^{\prime }}_2\frac{\partial }{\partial q_2}\left(\frac{h_2}{h_1\varpi }\right)=0,$ (13)

which by dividing with the product $Q_1{Q}_2$ becomes

$\frac{{Q^{″}}_1}{Q_1}\frac{h_1}{h_2\varpi }+\frac{{Q^{\prime }}_1}{Q_1}\frac{\partial }{\partial q_1}\left(\frac{h_1}{h_2\varpi }\right)+\frac{{Q^{″}}_2}{Q_2}\frac{h_2}{h_1\varpi }+\frac{{Q^{\prime }}_2}{Q_2}\frac{\partial }{\partial q_2}\left(\frac{h_2}{h_1\varpi }\right)=\mathrm{0,}$ (14)

where the primes denote the derivatives of the corresponding functions.

The “if” part: If Stokes stream equation separates variables, we will prove that the metric coefficients are given by (9) and (10).

Since $E^2\psi =0$ separates variables, due to the definition 1, the two dimensional PDE decomposes in two ordinary differential equations (ODEs). This is true only if the quantities $\frac{h_1}{h_2\varpi }$, $\frac{\partial }{\partial q_1}\left(\frac{h_1}{h_2\varpi }\right)$, $\frac{h_2}{h_1\varpi }$, $\frac{\partial }{\partial q_2}\left(\frac{h_2}{h_1\varpi }\right)$ can be written

as products of functions of one single variable each ( $q_1$ or $q_2$ ). In that case, (14) can be rewritten as a sum of two ODEs i.e. $\text{ODE}1\left(q_1\right)+\text{ODE}2\left(q_2\right)=0$, thus (9) and (10) hold.

The “only if” part: Assuming that $\frac{h_1}{h_2\varpi }=f_1{f}_2$ and $\frac{h_2}{h_1\varpi }=F_1{F}_2$ , we shall show that $E^2\psi =0$ separates variables.

Substituting (9), (10) in (12) we get

$Q_2{f}_2\frac{\text{d}}{\text{d}{q}_1}\left(f_1\frac{\text{d}{Q}_1}{\text{d}{q}_1}\right)+Q_1{F}_1\frac{\text{d}}{\text{d}{q}_2}\left(F_2\frac{\text{d}{Q}_2}{\text{d}{q}_2}\right)=0$ (15)

or

$\frac{\frac{\text{d}}{\text{d}{q}_1}\left(f_1\frac{\text{d}{Q}_1}{\text{d}{q}_1}\right)}{Q_1{F}_1}=-\frac{\frac{\text{d}}{\text{d}{q}_2}\left(F_2\frac{\text{d}{Q}_2}{\text{d}{q}_2}\right)}{Q_2{f}_2},$ (16)

which according to the definition 1, the equation separates variables. ¨

3.2. R-Separability of the Irrotational Stokes Equation

Next we provide the necessary and sufficient conditions, that the metric coefficients $h_1\mathrm{,}{h}_2$ and $\varpi$ of any axisymmetric coordinate system must satisfy in order to the irrotational Stokes equation admits R-separable solution.

Theorem 2. Let $\left(q_1\mathrm{,}{q}_2\mathrm{,}\phi \right)$ an axisymmetric system of coordinates with metric coefficients $h_1\mathrm{,}{h}_2$ and radial cylindrical coordinate $\varpi$ . The Stokes stream equation R-separates variables if and only if there exist functions $f_1\left(q_1\right)$ , $f_2\left(q_2\right)$ , $F_1\left(q_1\right)$ , $F_2\left(q_2\right)$ , $R\left(q_1\mathrm{,}{q}_2\right)$ , $R_1\left(q_1\right)$ , $R_2\left(q_2\right)$ such that

$\frac{h_1}{h_2\varpi }=R^2{f}_1{f}_2,$ (17)

$\frac{h_2}{h_1\varpi }=R^2{F}_1{F}_2,$ (18)

$\frac{1}{F_1}\frac{\partial }{\partial q_1}\left(f_1\frac{\partial R}{\partial q_1}\right)+\frac{1}{f_2}\frac{\partial }{\partial q_2}\left(F_2\frac{\partial R}{\partial q_2}\right)=R\left(R_1+R_2\right),$ (19)

where $R\left(q_1\mathrm{,}{q}_2\right)\ne g_1\left(q_1\right)g_2\left(q_2\right)$.

Proof. We assume that the function $\psi$ can be written in the form

$\psi \left(q_1,q_2\right)=\frac{Q_1\left(q_1\right)Q_2\left(q_2\right)}{R\left(q_1,q_2\right)}.$ (20)

Substituting (20) into (8) we arrive at

$Q_2\frac{\partial }{\partial q_1}\left(\frac{h_1}{h_2\varpi }\frac{\partial \frac{Q_1}{R}}{\partial q_1}\right)+Q_1\frac{\partial }{\partial q_2}\left(\frac{h_2}{h_1\varpi }\frac{\partial \frac{Q_2}{R}}{\partial q_2}\right)=0$ (21)

or

$\begin{array}{l}\frac{{Q^{″}}_1}{Q_1}\frac{h_1}{R{h}_2\varpi }+\frac{{Q^{\prime }}_1}{Q_1}\frac{1}{R^2}\left(R\frac{\partial \frac{h_1}{h_2\varpi }}{\partial q_1}-2\frac{h_1}{h_2\varpi }\frac{\partial R}{\partial q_1}\right)\\ +\frac{{Q^{″}}_2}{Q_2}\frac{h_2}{R{h}_1\varpi }+\frac{{Q^{\prime }}_2}{Q_2}\frac{1}{R^2}\left(R\frac{\partial \frac{h_2}{h_1\varpi }}{\partial q_2}-2\frac{h_2}{h_1\varpi }\frac{\partial R}{\partial q_2}\right)\\ -\left[\frac{\partial }{\partial q_1}\left(\frac{h_1}{R^2{h}_2\varpi }\frac{\partial R}{\partial q_1}\right)+\frac{\partial }{\partial q_2}\left(\frac{h_2}{R^2{h}_1\varpi }\frac{\partial R}{\partial q_2}\right)\right]=0.\end{array}$ (22)

The “if” part: If Stokes stream equation R-separates variables, then (17), (18), (19) hold.

Since $E^2\psi =0$ R-separates variables, from (22) yields that:

· each one of the functions $\frac{h_1}{R{h}_2\varpi }$, $\frac{1}{R^2}\left(R\frac{\partial \frac{h_1}{h_2\varpi }}{\partial q_1}-2\frac{h_1}{h_2\varpi }\frac{\partial R}{\partial q_1}\right)$, $\frac{h_2}{R{h}_1\varpi }$, $\frac{1}{R^2}\left(R\frac{\partial \frac{h_2}{h_1\varpi }}{\partial q_2}-2\frac{h_2}{h_1\varpi }\frac{\partial R}{\partial q_2}\right)$ has to be a product of three functions, one should be of the form $R\left(q_1\mathrm{,}{q}_2\right)$ and the other two functions should be of one single variable each, which according to definition 2 proves (17), (18) and

· the function $\left[\frac{\partial }{\partial q_1}\left(\frac{h_1}{R^2{h}_2\varpi }\frac{\partial R}{\partial q_1}\right)+\frac{\partial }{\partial q_2}\left(\frac{h_2}{R^2{h}_2\varpi }\frac{\partial R}{\partial q_2}\right)\right]$ can be written as a product of the functions R and $\Phi$ defined appropriate to allow separation of variables.

From (21), using the notation imposed in (17) and (18) we obtain

$f_2{Q}_2\frac{\partial }{\partial q_1}\left(R^2{f}_1\frac{\partial \frac{Q_1}{R}}{\partial q_1}\right)+F_1{Q}_1\frac{\partial }{\partial q_2}\left(R^2{F}_2\frac{\partial \frac{Q_2}{R}}{\partial q_2}\right)=0.$ (23)

Calculating the partial derivatives of (23) we get

$\begin{array}{l}{f}_2{Q}_{2}R\frac{\text{d}}{\text{d}{q}_1}\left(f_1\frac{\text{d}{Q}_1}{\text{d}{q}_1}\right)-f_2{Q}_2{Q}_1\frac{\partial }{\partial q_1}\left(f_1\frac{\partial R}{\partial q_1}\right)\\ +F_1{Q}_{1}R\frac{\text{d}}{\text{d}{q}_2}\left(F_2\frac{\text{d}{Q}_2}{\text{d}{q}_2}\right)-F_1{Q}_1{Q}_2\frac{\partial }{\partial q_2}\left(F_2\frac{\partial R}{\partial q_2}\right)=\mathrm{0,}\end{array}$ (24)

which indicates that (19) is also sufficient for the R-separability of the irrotational Stokes equation. Furthermore function $\Phi$ is defined as $\Phi =R{F}_1{f}_2\left(R_1+R_2\right)$ which allows R-separation.

The “only if” part: Assuming that $\frac{1}{F_1}\frac{\partial }{\partial q_1}\left(f_1\frac{\partial R}{\partial q_1}\right)+\frac{1}{f_2}\frac{\partial }{\partial q_2}\left(F_2\frac{\partial R}{\partial q_2}\right)=R\left(R_1+R_2\right)$, $\frac{h_1}{h_2\varpi }=R^2{f}_1{f}_2$ and $\frac{h_2}{h_1\varpi }=R^2{F}_1{F}_2$ then equation $E^2\psi =0$ R-separates variables.

If we substitute (17), (18) in (21) we have

$Q_2{f}_2\frac{\partial }{\partial q_1}\left(f_{1}R\frac{\text{d}{Q}_1}{\text{d}{q}_1}-f_1{Q}_1\frac{\partial R}{\partial q_1}\right)+Q_1{F}_1\frac{\partial }{\partial q_2}\left(F_{2}R\frac{\text{d}{Q}_2}{\text{d}{q}_2}-F_2{Q}_2\frac{\partial R}{\partial q_2}\right)=0$ (25)

or

$\begin{array}{l}R\left[f_2{Q}_2\frac{\text{d}}{\text{d}{q}_1}\left(f_1\frac{\text{d}{Q}_1}{\text{d}{q}_1}\right)+F_1{Q}_1\frac{\text{d}}{\text{d}{q}_2}\left(F_2\frac{\text{d}{Q}_2}{\text{d}{q}_2}\right)\right]\\ =Q_1{Q}_2\left[F_1\frac{\partial }{\partial q_2}\left(F_2\frac{\partial R}{\partial q_2}\right)+f_2\frac{\partial }{\partial q_1}\left(f_1\frac{\partial R}{\partial q_1}\right)\right]\end{array}$ (26)

and using (19) we obtain

$\frac{1}{F_1{Q}_1}\frac{\text{d}}{\text{d}{q}_1}\left(f_1\frac{\text{d}{Q}_1}{\text{d}{q}_1}\right)+\frac{1}{f_2{Q}_2}\frac{\text{d}}{\text{d}{q}_2}\left(F_2\frac{\text{d}{Q}_2}{\text{d}{q}_2}\right)=R_1+R_2\mathrm{,}$ (27)

which shows that the equation $E^2\psi =0$ separates variables. ¨

3.3. Inverted Coordinate Systems.

Next, we expand the proposed methodology to treat the case of the inverted coordinate systems (with respect to a sphere of radius $b>0$ ).

Lemma 1. Let an axisymmetric system of coordinates $\left(q_1\mathrm{,}{q}_2\mathrm{,}\phi \right)$ with metric coefficients $h_1\mathrm{,}{h}_2$ , radial cylindrical coordinate $\varpi$ and the corresponding system of coordinates under the inversion with respect to a sphere of radius $b>0$ having metric coefficients ${h^{\prime }}_1\mathrm{,}{h^{\prime }}_2$ and radial cylindrical coordinate ${\varpi }^{\prime }$, then the following relations, interconnecting the metric coefficients hold true.

${h^{\prime }}_1=\frac{r^2}{b^2}{h}_1,$ (28)

${h^{\prime }}_2=\frac{r^2}{b^2}{h}_2,$ (29)

${\varpi }^{\prime }=\frac{b^2}{r^2}\varpi .$ (30)

Proof. Any point $\left(x_1\mathrm{,}{x}_2\mathrm{,}{x}_3\right)$ in the Cartesian coordinate system, is expressed in an axisymmetric system of coordinates as $\left(q_1\mathrm{,}{q}_2\mathrm{,}\phi \right)$. If $\left({x^{\prime }}_1\mathrm{,}{x^{\prime }}_2\mathrm{,}{x^{\prime }}_3\right)$ is the image of the point $\left(x_1\mathrm{,}{x}_2\mathrm{,}{x}_3\right)$ under an inverse transformation with respect to a sphere of radius $b>0$, it yields

$\{\begin{array}{l}{x^{\prime }}_1=\frac{1}{{\rho }^2+z^2}\rho \left(q_1,q_2\right)\cos \phi \\ {x^{\prime }}_2=\frac{1}{{\rho }^2+z^2}\rho \left(q_1,q_2\right)\sin \phi \\ {x^{\prime }}_3=\frac{1}{{\rho }^2+z^2}z\left(q_1,q_2\right)\end{array}$ (31)

since $r^2=x_1^2+x_2^2+x_3^2={\rho }^2+z^2$. The new system of coordinates is also axisymmetric with

${\rho }^{\prime }\left(q_1\mathrm{,}{q}_2\right)=\frac{1}{r^2}\rho \left(q_1\mathrm{,}{q}_2\right)\mathrm{,}$ (32)

$z^{\prime }\left(q_1\mathrm{,}{q}_2\right)=\frac{1}{r^2}z\left(q_1\mathrm{,}{q}_2\right)$ (33)

and the corresponding metric coefficients (4), (5) are defined as

${h^{\prime }}_1=\frac{1}{\sqrt{{\left(\frac{\partial {\rho }^{\prime }}{\partial q_1}\right)}^2+{\left(\frac{\partial z^{\prime }}{\partial q_1}\right)}^2}}\mathrm{,}$ (34)

${h^{\prime }}_2=\frac{1}{\sqrt{{\left(\frac{\partial {\rho }^{\prime }}{\partial q_2}\right)}^2+{\left(\frac{\partial z^{\prime }}{\partial q_2}\right)}^2}}\mathrm{.}$ (35)

Calculating the partial derivatives of ${\rho }^{\prime }\left(q_1\mathrm{,}{q}_2\right)\mathrm{,}{z}^{\prime }\left(q_1\mathrm{,}{q}_2\right)$ with respect to $q_1\mathrm{,}{q}_2$ and substituting into (34), (35), we obtain that (28), (29) are true.

Furthermore, the radial cylindrical coordinate (6) is given by

${\varpi }^{\prime }=\left|{\rho }^{\prime }\left(q_1\mathrm{,}{q}_2\right)\right|\mathrm{,}$ (36)

so from (32), (6) it yields that (30) is also true. ¨

This way we provided relations interconnecting the metric coefficients of any axisymmetric coordinate system and its inverse.

4. Applications

4.1. Simple Separation of Stokes Stream Equation in the Oblate Spheroid Coordinate System

In this section we will demonstrate that in the oblate geometry equation $E^2\psi =0$ separates variables. It is known that any point $\left(x_1\mathrm{,}{x}_2\mathrm{,}{x}_3\right)$ in the Cartesian coordinate system, is expressed using the oblate spheroid coordinates $\left(\lambda \mathrm{,}\zeta \mathrm{,}\phi \right)$ where $\lambda \in ℝ$, $\zeta \in \left[-\mathrm{1,1}\right]$ and $\alpha >0$ is the semifocal distance, through the relations

$\{\begin{array}{l}{x}_1=\alpha \sqrt{{\lambda }^2+1}\sqrt{1-{\zeta }^2}\cos \left(\phi \right)\\ x_2=\alpha \sqrt{{\lambda }^2+1}\sqrt{1-{\zeta }^2}\sin \left(\phi \right)\\ x_3=\alpha \lambda \zeta \end{array}$ (37)

For constant λ we obtain oblate spheroidal coordinate surfaces in Figure 1.

Using (4), (5) we obtain

$h_1=\frac{\sqrt{{\lambda }^2+1}}{a\sqrt{{\lambda }^2+{\zeta }^2}},h_2=\frac{\sqrt{1-{\zeta }^2}}{a\sqrt{{\lambda }^2+{\zeta }^2}}$ (38)

and since $\varpi =a\sqrt{{\lambda }^2+1}\sqrt{1-{\zeta }^2}$ we derive

$\frac{h_1}{h_2\varpi }=\frac{1}{a\left(1-{\zeta }^2\right)},\frac{h_2}{h_1\varpi }=\frac{1}{a\left(1+{\lambda }^2\right)},$ (39)

while from (9), (10) assuming $q_1=\lambda ,q_2=\zeta$, we get

$f_1\left(\lambda \right)=\frac{1}{a},f_2\left(\zeta \right)=\frac{1}{1-{\zeta }^2},F_1\left(\lambda \right)=\frac{1}{1+{\lambda }^2},F_2\left(\zeta \right)=\frac{1}{a}.$ (40)

These calculations prove that theorem 1 holds, therefore Stokes stream equation separates variables in the oblate spheroidal coordinate system. This result verify the findings by Dassios et al. [11], where they showed that Stokes equation separates variables in the oblate geometry, taking into account the proof of the simple separability of the equation in the prolate geometry and the transformation $\tau =i\lambda ,c=-ia,\tau \ge 1,c>0$ which connects the oblate coordinate system and the prolate one $\left(\tau \mathrm{,}\zeta \mathrm{,}\varphi \right)\mathrm{,}\zeta \in \left[-\mathrm{1,1}\right]$. The eigenfunctions ${\Theta }_n^{\left(i\right)}\left(\lambda ,\zeta \right),i=1,2,3,4$ in the oblate spheroid coordinate system are

$(\begin{array}{l}{\Theta }_n^{\left(1\right)}\left(\lambda ,\zeta \right)=G_n\left(i\lambda \right)G_n\left(\zeta \right)\\ {\Theta }_n^{\left(2\right)}\left(\lambda ,\zeta \right)=G_n\left(i\lambda \right)H_n\left(\zeta \right)\\ {\Theta }_n^{\left(3\right)}\left(\lambda ,\zeta \right)=H_n\left(i\lambda \right)G_n\left(\zeta \right)\\ {\Theta }_n^{\left(4\right)}\left(\lambda ,\zeta \right)=H_n\left(i\lambda \right)H_n\left(\zeta \right)\end{array}$ (41)

where $G_n\mathrm{,}{H}_n$ are Gegenbauer functions of the first and the second kind respectively [34]. These eigenfunctions form a basis for the solution space of the irrotational flow problems around oblate spheroidal bodies. In Figures 2-5 we

Figure 1. The oblate spheroid.

Figure 2. Streamlines for ${\Theta }_2^{\left(4\right)}$.

Figure 3. Streamlines for ${\Theta }_4^{\left(2\right)}$.

Figure 4. Streamlines for ${\Theta }_4^{\left(3\right)}$.

Figure 5. Streamlines for ${\Theta }_4^{\left(4\right)}$.

present sample streamlines of eigenfunctions ${\Theta }_n^{\left(i\right)}\left(\lambda ,\zeta \right)$ in the oblate spheroid coordinate system in the plane $x_2=0$.

4.2. R-Separation of Stokes Stream Equation in the Inverted Oblate Spheroid Coordinate System

Next we will prove that the equation ${E^{\prime }}^2{\psi }_{inv\mathrm{.}}=0$ R-separates variables in the inverted oblate geometry, where ${E^{\prime }}^2$ denotes the Stokes operator in the inverted system. Any point $\left({x^{\prime }}_1\mathrm{,}{x^{\prime }}_2\mathrm{,}{x^{\prime }}_3\right)$ in the Cartesian coordinate system is expressed as

$\left({x^{\prime }}_1\mathrm{,}{x^{\prime }}_2\mathrm{,}{x^{\prime }}_3\right)=\frac{a^2}{{\lambda }^2-{\zeta }^2+1}\left(x_1\mathrm{,}{x}_2\mathrm{,}{x}_3\right)\mathrm{.}$ (42)

For constant λ we obtain inverse oblate spheroidal coordinate surfaces in Figure 6.

The metric coefficients ${h^{\prime }}_1\mathrm{,}{h^{\prime }}_2$ and the radial cylindrical coordinate ${\varpi }^{\prime }$ are

${h^{\prime }}_1=\frac{\sqrt{{\lambda }^2+1}\left({\lambda }^2-{\zeta }^2+1\right)}{a\sqrt{{\lambda }^2+{\zeta }^2}},{h^{\prime }}_2=\frac{\sqrt{1-{\zeta }^2}\left({\lambda }^2-{\zeta }^2+1\right)}{a\sqrt{{\lambda }^2+{\zeta }^2}},$ (43)

${\varpi }^{\prime }=\frac{a\sqrt{{\lambda }^2+1}\sqrt{1-{\zeta }^2}}{{\lambda }^2-{\zeta }^2+1}$ (44)

and we calculate that

$\frac{{h^{\prime }}_1}{{h^{\prime }}_2{\varpi }^{\prime }}=\frac{{\lambda }^2-{\zeta }^2+1}{a\left(1-{\zeta }^2\right)},\frac{{h^{\prime }}_2}{{h^{\prime }}_1{\varpi }^{\prime }}=\frac{{\lambda }^2-{\zeta }^2+1}{a\left(1+{\lambda }^2\right)}.$ (45)

We observe that Equation (45) do not fulfill the conditions set in (9), (10) and therefore theorem 1 does not hold. Subsequently, we investigate whether the conditions of theorem 2 are satisfied. From (45) with (17), (18) we get

$f_1\left(\lambda \right)=1,f_2\left(\zeta \right)=\frac{1}{1-{\zeta }^2},F_1\left(\lambda \right)=\frac{1}{{\lambda }^2+1},F_2\left(\zeta \right)=1$ (46)

and $R\left(\lambda \mathrm{,}\zeta \right)=\sqrt{{\lambda }^2-{\zeta }^2+1}$ since $q_1=\lambda ,q_2=\zeta$.

Moreover we calculate

$\frac{1}{F_1}\frac{\partial }{\partial q_1}\left(f_1\frac{\partial R}{\partial q_1}\right)+\frac{1}{f_2}\frac{\partial }{\partial q_2}\left(F_2\frac{\partial R}{\partial q_2}\right)=0,$ (47)

which verifies (19) when $R_1=R_2=0$. This proves that Stokes stream equation in inverted geometry R-separates variables with $R\left(\lambda \mathrm{,}\zeta \right)=\sqrt{{\lambda }^2-{\zeta }^2+1}$.

This result is in agreement with the one given in [11], where the obtained eigenfunctions of Stokes stream equation were

${{\Theta }^{\prime }}_n^{\left(i\right)}\left(\lambda ,\zeta \right)=\frac{1}{\sqrt{{\lambda }^2-{\zeta }^2+1}}{\Theta }_n^{\left(i\right)}\left(\lambda ,\zeta \right),i=1,2,3,4,n=0,1,2,\cdots$ (48)

Figures 7-10 show sample streamlines for the eigenfunctions of the Stokes operator in the inverted oblate spheroid in the plane $x_2=0$.

Figure 6. The inverted oblate spheroid.

Figure 7. Streamlines for ${{\Theta }^{\prime }}_1^{\left(3\right)}$.

Figure 8. Streamlines for ${{\Theta }^{\prime }}_3^{\left(2\right)}$.

Figure 9. Streamlines for ${{\Theta }^{\prime }}_4^{\left(2\right)}$.

Figure 10. Streamlines for ${{\Theta }^{\prime }}_4^{\left(3\right)}$.

Furthermore, taking into account (38), (43), (44) we derive that (28), (29), (30) are true if $b=a$, which means that since irrotational Stokes equation separates variables in the oblate spheroid coordinate system, it R-separates variables in its inverted one, as it was stated in lemma 1.

4.3. Separability Results in Known Orthogonal Axisymmetric Systems of Coordinates

In this section we investigate whether theorems 1 and 2 hold true in various axisymmetric coordinates [33] and we reveal the particular type of separability that the irrotational Stokes flow equation $E^2\psi =0$ admits.

Particularly, in the spherical coordinate system we obtain $\left(r\mathrm{,}\zeta \mathrm{,}\phi \right)\mathrm{,}r\ge \mathrm{0,}\zeta \in \left[-\mathrm{1,1}\right]$

$\frac{h_1}{h_2\varpi }=\frac{1}{1-{\zeta }^2},\frac{h_2}{h_1\varpi }=\frac{1}{r^2},$ (49)

in the prolate spheroid $\left(r,\zeta ,\phi \right),\tau \ge 1,\zeta \in \left[-1,1\right],\alpha >0$ we get

$\frac{h_1}{h_2\varpi }=\frac{1}{a\left(1-{\zeta }^2\right)},\frac{h_2}{h_1\varpi }=\frac{1}{a\left({\tau }^2-1\right)},$ (50)

in the parabolic coordinate system $\left(\mu \mathrm{,}\nu \mathrm{,}\phi \right)\mathrm{,}\mu \mathrm{,}\nu \ge 0$ it yields

$\frac{h_1}{h_2\varpi }=\frac{h_2}{h_1\varpi }=\frac{1}{\mu \nu },$ (51)

which all verify successively (9), (10). Thus the conditions of theorem 1 are satisfied so Stokes equation separates variables in spherical, parabolic and spheroidal geometries.

Moreover, in the tangent sphere coordinate system $\left(\mu ,\nu ,\phi \right),\mu >0,\nu \in ℝ$ we derive

$\frac{h_1}{h_2\varpi }=\frac{h_2}{h_1\varpi }=\frac{{\mu }^2+{\nu }^2}{\mu },\frac{1}{F_1}\frac{\partial }{\partial q_1}\left(f_1\frac{\partial R}{\partial q_1}\right)+\frac{1}{f_2}\frac{\partial }{\partial q_2}\left(F_2\frac{\partial R}{\partial q_2}\right)=0,$ (52)

in the cardioid coordinate system $\left(\mu ,\nu ,\phi \right)\mathrm{,}\mu \mathrm{,}\nu \ge 0$ we get

$\frac{h_1}{h_2\varpi }=\frac{h_2}{h_1\varpi }=\frac{{\left({\mu }^2+{\nu }^2\right)}^2}{\mu \nu },\frac{1}{F_1}\frac{\partial }{\partial q_1}\left(f_1\frac{\partial R}{\partial q_1}\right)+\frac{1}{f_2}\frac{\partial }{\partial q_2}\left(F_2\frac{\partial R}{\partial q_2}\right)=0,$ (53)

in the bispherical coordinate system $\left(\eta \mathrm{,}\theta \mathrm{,}\phi \right)\mathrm{,}\eta \in ℝ\mathrm{,}\theta \in \left[\mathrm{0,}\pi \right)\mathrm{,}\alpha >0$ we obtain

$\frac{h_1}{h_2\varpi }=\frac{h_2}{h_1\varpi }=\frac{\cosh \left(\eta \right)-\cos \left(\theta \right)}{a\sin \left(\theta \right)},\frac{1}{F_1}\frac{\partial }{\partial q_1}\left(f_1\frac{\partial R}{\partial q_1}\right)+\frac{1}{f_2}\frac{\partial }{\partial q_2}\left(F_2\frac{\partial R}{\partial q_2}\right)=\frac{R}{4},$ (54)

in the toroidal coordinate system $\left(\eta ,\theta ,\phi \right),\eta \ge 0,\theta \in \left(-\pi ,\pi \right],\alpha >0$ we get

$\frac{h_1}{h_2\varpi }\mathrm{<mo>\; =\; </mo>}\frac{h_2}{h_1\varpi }\mathrm{<mo>\; =\; </mo>}\frac{cosh\mathrm{<mo\; stretchy="false">\; (\; </mo>}\eta \mathrm{<mo\; stretchy="false">\; )\; </mo>}-cos\mathrm{<mo\; stretchy="false">\; (\; </mo>}\theta \mathrm{<mo\; stretchy="false">\; )\; </mo>}}{asinh\mathrm{<mo\; stretchy="false">\; (\; </mo>}\eta \mathrm{<mo\; stretchy="false">\; )\; </mo>}}\mathrm{,}\frac{1}{F_1}\frac{\partial }{\partial q_1}\left(f_1\frac{\partial R}{\partial q_1}\right)+\frac{1}{f_2}\frac{\partial }{\partial q_2}\left(F_2\frac{\partial R}{\partial q_2}\right)\mathrm{<mo>\; =\; </mo>}-\frac{R}{4}\mathrm{,}$ (55)

and in the inverted prolate coordinate system $\left(\eta ,\theta ,\phi \right),\eta \ge 0,\theta \in \left[0,\pi \right],\alpha >0$ we have

$\frac{h_1}{h_2\varpi }=\frac{h_2}{h_1\varpi }=\frac{{\cosh }^2\left(\eta \right)-{\sin }^2\left(\theta \right)}{a\sin \left(\theta \right)\sinh \left(\eta \right)},\frac{1}{F_1}\frac{\partial }{\partial q_1}\left(f_1\frac{\partial R}{\partial q_1}\right)+\frac{1}{f_2}\frac{\partial }{\partial q_2}\left(F_2\frac{\partial R}{\partial q_2}\right)=0,$ (56)

which verify (17), (18), (19). Therefore the conditions of theorem 2 are satisfied so Stokes equation R-separates variables in tangent sphere, cardioid, bishperical, toroidal and inverse prolate geometries. For convenience, we group the outcomes together in Tables 1-3.

5. Discussion

When a solution is obtained in separable form (product of functions of one variable alone) qualitative and quantitative information can be extracted by studying the behaviour of each of these functions independently, e.g. behaviour at infinity, close to singularities, etc. Additionally, when dealing with Boundary Value Problems, the appropriate curvilinear system is chosen so that the boundary

Table 1. Simple separation of Stokes operator in axisymmetric systems of coordinates.

Table 2. R-separation of stokes operator in axisymmetric systems of coordinates (part 1).

coincides with one of the coordinate surfaces which allows for simpler calculations, clear and comprehensive results. Conclusively, the separation of variables or the Fourier method, apart from a convenient method for deriving solutions of PDEs, it is also a method for revealing inherent characteristics of the problem.

Table 3. R-separation of stokes operator in axisymmetric systems of coordinates (part 2).

Some crucial questions are answered in the present manuscript, regarding the different kinds of separability one can have when solving irrotational Stokes flow problems in different axi-symmetric geometries. We provide “necessary and sufficient conditions” for the two kinds of separation: simple and R-separation, for any axisymmetric system of coordinates, in a general form. We also treated the case of the inverse of these systems (lemma 1). Furthermore, we applied the developed theory (theorems 1 and 2) to the oblate spheroidal coordinate system and proved the separability of the irrotational Stokes equation in this system and the R-separability of the irrotational Stokes equation in the inverted oblate spheroidal coordinate system.

More specifically, we provide necessary and sufficient conditions for simple separation (theorem 1) and R-separation (theorem 2) for the irrotational Stokes equation in any axisymmetric coordinate system of the general form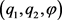. The function 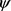may then be obtained as a combination of the solutions of the corresponding Ordinary Differential Equations to which equation decomposes. Our results are based on the form that the metric coefficients 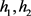and the radial cylindrical coordinate get in any axisymmetric

coordinate system. We calculate the quantities and examine whether

conditions (9), (10), (17), (18) hold. If (9), (10) are satisfied the method of separation of variables may be applied and obtain results. Furthermore if (17), (18) hold true, we can calculate the function R and when the requirements for (19) are also met, then the irrotational Stokes equation can be solved by employing the method of R-separation of variables. Additionally, we developed relations connecting the metric coefficients and the radial cylindrical coordinate in any axisymmetric coordinate system and its inverted one (lemma 1). Applying theorems 1, 2 and lemma 1 we reach at the following results:

· When irrotational Stokes equation separates variables in an axisymmetric system of coordinates, then the irrotational Stokes equation R-separates variables in the corresponding inverted system of coordinates, with, where r is the Euclidean distance, expressed in the parameters of the particular coordinate system.

· When irrotational Stokes equation R-separates variables in an axisymmetric system of coordinates, then the irrotational Stokes equation also R-separates variables in the corresponding inverted system of coordinates if (19) is also true.

This property, allows for the derivation of an analytical solution of the irrotational Stokes flow in a system, whenever the analytical solution of the corresponding problem in the inverted one is known. As an illustration, we employ the inverted oblate spheroidal coordinate system and prove the R-separability of through the Lemma using the separable form of the irrotational Stokes equation in the oblate coordinates, which agrees with already obtained results given in [29]. These theorems may serve as a priori, solvability criteria, preventing from man or computer waste of effort when seeking for solutions for the axisymmetric Stokes flow equations (rotational and irrotational), also carving this way, a path for further utilization.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

References

[1]	Stokes, G.G. (1851) On the Effect of the Internal Friction of Fluids on the Motion of Pendulums. Transactions of the Cambridge Philosophical Society, 9, 8-106.
[2]	Happel, J. and Brenner, H. (1991) Low Reynolds Number Hydrodynamics. Kluwer Academic Publishers, Dordrecht.
[3]	Stimpson, M. and Jeffery, B.G. (1926) The Motion of Two Spheres in a Viscous Fluid. Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 111, 110-116. https://doi.org/10.1098/rspa.1926.0053
[4]	Padmavathi, S.B., Amaranath, T. and Nigam, D.S. (1993) Stokes Flow past a Porous Sphere Using Brinkman’s Model. Zeitschrift für Angewandte Mathematik und Physik, 44, 929-939. https://doi.org/10.1007/BF00942818
[5]	Sekhar, R.P.G. and Amaranath, T. (2000) Stokes Flow inside a Porous Spherical Shell. Zeitschrift für Angewandte Mathematik und Physik, 51, 481-490. https://doi.org/10.1007/s000330050009
[6]	Elasmi, L., Berzig, M. and Feuillebois, F. (2003) Stokes Flow for the Axisymmetric Motion of Several Spherical Particles Perpendicular to a Plane Wall. Zeitschrift für Angewandte Mathematik und Physik, 54, 304-327. https://doi.org/10.1007/s000330300006
[7]	Padmavathi, S.B., Amaranath, T. and Nigam, D.S. (1993) Stokes Flow past a Sphere with Mixed Slip-Stick Boundary Conditions. Fluid Dynamics Research, 11, 229-234. https://doi.org/10.1016/0169-5983(93)90113-O
[8]	Guémas, M., Sellier, A. and Pigeonneau, F. (2016) Low-Reynolds-Number Rising of a Bubble near a Free Surface at Vanishing Bond Number. Physics of Fluids, 28, Article ID: 063102. https://doi.org/10.1063/1.4953467
[9]	Ageeva, I. and Osiptsova, N.A. (2019) Stokes Flow in a Microchannel with Superhydrophobic Walls. Fluid Dynamics, 54, 203-215. https://doi.org/10.1134/S0015462819020010
[10]	Deo, S. and Yadav, A.P. (2008) Stokes Flow past a Swarm of Porous Nanocylindrical Particles Enclosing a Solid Core. International Journal of Mathematics and Mathematical Sciences, 2008, Article ID: 651910. https://doi.org/10.1155/2008/651910
[11]	Dassios, G., Hadjinicolaou, M. and Payatakes, A.C. (1994) Generalized Eigenfunctions and Complete Semiseparable Solutions for Stokes Flow in Spheroidal Coordinates. Quarterly of Applied Mathematics, 52, 157-191. https://doi.org/10.1090/qam/1262325
[12]	Dassios, G., Hadjinicolaou, M., Coutelieris, F.A. and Payatakes, A.C. (1995) Stokes Flow in Spheroidal Particle in Cell Models with Happel and Kuwabara Boundary Conditions. International Journal of Engineering Science, 33, 1465-1490. https://doi.org/10.1016/0020-7225(95)00010-U
[13]	Hadjinicolaou, M. and Protopapas, E. (2020) A Microscale Mathematical Blood Flow Model for Understanding Cardiovascular Diseases. In: GeNeDis 2018, Springer, Berlin, 373-387.
[14]	Deo, S. and Datta, S. (2003) Stokes Flow past a Fluid Prolate Spheroid. Indian Journal of Pure and Applied Mathematics, 34, 755-764.
[15]	Moosaie, A. and Atefi, G. (2008) Slow Motion of a Rotating Circular Cylinder through a Micropolar Fluid. Archives of Mechanics, 60, 199-220.
[16]	Leshansky, M.A., Kenneth, O., Gat, O. and Avron, E.J. (2007) A Frictionless Microswimmer. New Journal of Physics, 9, 145. https://doi.org/10.1088/1367-2630/9/5/145
[17]	Sturzenegger, C.J., Sarasúa, G.L. and Martí, C.A. (2012) Analytical Solutions for the Axisymmetric Flow inside a Cylindrical Container with a Rod along the Axis at Low Reynolds Numbers. Journal of Fluids and Structures, 28, 473-479. https://doi.org/10.1016/j.jfluidstructs.2011.11.002
[18]	Dassios, G., Hadjinicolaou, M. and Protopapas, E. (2012) Blood Plasma Flow past a Red Blood Cell: Mathematical Modelling and Analytical Treatment. Mathematical Methods in the Applied Sciences, 35, 1547-1563. https://doi.org/10.1002/mma.2540
[19]	Hadjinicolaou, M., Kamvyssas, G. and Protopapas, E. (2013) Stokes Flow Applied to the Sedimentation of a Red Blood Cell. Quarterly of Applied Mathematics, 73, 511-523.
[20]	Hadjinicolaou, M. (2015) A Mathematical Model for the Blood Plasma Flow around Two Aggregated Low Density Lipoproteins. In: GeNeDis 2014, Advanced Experimental Medicine and Biology Vol. 820, Springer International Publishing, Berlin, 173-184.
[21]	Hadjinicolaou, M. and Protopapas, E. (2015) Translation of Two Aggregated Low Density Lipoproteins within Blood Plasma. A Mathematical Model. In: GeNeDis, Advanced Experimental Medicine and Biology Vol. 820, Springer International Publishing, Berlin, 185-192. https://doi.org/10.1007/978-3-319-09012-2_12
[22]	Lamb, H. (1945) Hydrodynamics. 6th Edition, Dover, New York, Cambridge Univercity. Press, Cambridge, 1932.
[23]	Oberbeck, A. (1876) Ueber Stationäre Flüssigkeitsbewegungen mit Berücksichtigung der inneren Reibung. Journal für die Reine und Angewandte Mathematik, 81, 62-80. https://doi.org/10.1515/crll.1876.81.62
[24]	Sampson, A.R. (1891) On Stoke’s Current Function. Philosophical Transactions of the Royal Society of London, 182, 449-518. https://doi.org/10.1098/rsta.1891.0012
[25]	Payne, E.L. and Pell, H.W. (1960) The Stokes Flow Problem for a Class of Axially Symmetric Bodies. Journal of Fluid Mechanics, 45, 529-549. https://doi.org/10.1017/S002211206000027X
[26]	Zlatanovski, T. (1999) Axisymmetric Creeping Flow past a Porous Prolate Spheroidal Particle Using the Brinkman Model. The Quarterly Journal of Mechanics and Applied Mathematics, 52, 111-126. https://doi.org/10.1093/qjmam/52.1.111
[27]	Hadjinicolaou, M. and Protopapas, E. (2013) On the R-Semiseparation of the Stokes Bi-Stream Operator in the Inverted Prolate Spheroidal Coordinates. Mathematical Methods in the Applied Sciences, 37, 207-211. https://doi.org/10.1002/mma.2841
[28]	Hadjinicolaou, M. and Protopapas, E. (2015) Spectral Decomposition of the Stokes Flow Operators in the Inverted Prolate Spheroidal Coordinates. The IMA Journal of Applied Mathematics, 80, 1475-1491. https://doi.org/10.1093/imamat/hxv003
[29]	Hadjinicolaou, M. and Protopapas, E. (2016) Eigenfunction Expansions for the Stokes Flow Operators in the Inverted Oblate Coordinate System. Mathematical Problems in Engineering, 2016, Article ID: 9049131. https://doi.org/10.1155/2016/9049131
[30]	Deo, S. and Tiwari, A. (2008) On the Solution of a Partial Differential Equation Representing Irrotational Flow in Bispherical Polar Coordinates. Applied Mathematics and Computation, 205, 475-477. https://doi.org/10.1016/j.amc.2008.08.023
[31]	Hadjinicolaou, M. and Protopapas, E. (2020) Separability of Stokes Equations in Axisymmetric Geometries. Journal of Applied Mathematics and Physics, 8, 315-348. https://doi.org/10.4236/jamp.2020.82026
[32]	Moon, P. and Spencer, D.E. (1961) Field Theory Handbook. Springer-Verlag, Berlin. https://doi.org/10.1007/978-3-642-53060-9
[33]	Morse, P.M. and Feshbach, H. (1953) Methods of Theoretical Physics. McGraw-Hill, New York.
[34]	Lebedev, N.N. (1972) Special Functions and Their Applications. Dover Publications, Mineola.