1. Introduction
With the rapid development of the internet, computer science and data information technology, we are facing a real world with more and more dynamic characteristics, often dealing with a large number of high-dimensional random data, and the uncertainty is becoming more and more large. The Choquet expectation theory cannot satisfy the dynamic economic model in the risk study, such as financial risk with highly dynamic and complex characteristics. By introducing a backward stochastic differential equation (BSDE) in typical probability space, in 1997, Peng [1] constructs a new class of nonlinear expectations which are uniquely determined by the generating function g of BSDE, which is named g-expectation. In a sense, the discovery establishes the theoretical basis of dynamic nonlinear mathematical expectation. With more and more scholars studying, g-expectation has become a powerful tool for studying recursive utility theory and financial risk measurement [2] [3] [4] . The concept of g-expectation can be applied to handle a set 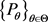 of uncertain probabilities by reference probability P. However, especially for
of uncertain probabilities by reference probability P. However, especially for  and
and , g-expectation is no longer applicable. Peng [5] introduced a new nonlinear mathematical expectation-G-expectation. Because the G-expectation constructive risk measure is a consistent risk measure, the theory has an important application in financial theory [6] [7] [8] [9] . In G-expectation theory, G-normal distribution theory is a sublinear expectation defined by Peng in the space of global continuous orbit. Next, there are concepts, which are introduced, such as a new stochastic process called G-Brownian motion, G-Itô integral and so on. Subsequently, the law of large numbers and central limit theorems under G-expectation are also proved [10] .
, g-expectation is no longer applicable. Peng [5] introduced a new nonlinear mathematical expectation-G-expectation. Because the G-expectation constructive risk measure is a consistent risk measure, the theory has an important application in financial theory [6] [7] [8] [9] . In G-expectation theory, G-normal distribution theory is a sublinear expectation defined by Peng in the space of global continuous orbit. Next, there are concepts, which are introduced, such as a new stochastic process called G-Brownian motion, G-Itô integral and so on. Subsequently, the law of large numbers and central limit theorems under G-expectation are also proved [10] .
Now based on the multiple G-Itô integral, scholars get the relationship between Hermite polynomials and multiple G-Itô integrals. Stratonovish [11] introduced the Brown movement. The problems related to the Stratonovish integral are not easy to solve. In 2012, Yin [12] introduced one weight G-Stratonovish integral of Brownian motion.
In this paper, according to the definition of Stratonovish integral of Brownian motion in G-expectation space, we not only introduce the multiple G-Stratonovish integral of Brownian motion but also obtain the relationship between Hermite polynomials and multiple G-Stratonovish integrals.
The structure of this paper is as follows: in Section 2, we first introduce the basic theoretical framework of nonlinear expectation related to the main concepts. In Section 3, two related theorems which are the relationships between Hermite polynomials and multiple G-Stratonovish integrals are given by mathematical induction for the G-Stratonovish integral of Brownian motion.
2. Preliminaries and Notation
Let 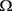 be a given set and let
be a given set and let  be a linear space of real valued functions defined on
be a linear space of real valued functions defined on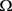 . In this paper, we suppose that
. In this paper, we suppose that  satisfies
satisfies  for each constant c and
for each constant c and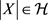 . The space
. The space 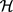 can be considered as the space of random variables. Peng [13] gave the nonlinear G-mathematical expectation and G-normal distribution as follows.
can be considered as the space of random variables. Peng [13] gave the nonlinear G-mathematical expectation and G-normal distribution as follows.
Definition 1 [13] We define a functional sublinear expectation 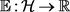 by
by
1) Monotonicity: 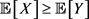 if
if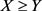 .
.
2) Constant preserving:  for
for 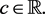
3) Sub-additivity: For each ,
, .
.
4) Positive homogeneity: 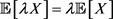 for
for![]() .
.
We call a sublinear expectation space, which is the triple![]() . If 1) and 2) are satisfied,
. If 1) and 2) are satisfied, ![]() is called a nonlinear expectation and the triple
is called a nonlinear expectation and the triple ![]() is called a nonlinear expectation space.
is called a nonlinear expectation space.
Definition 2 [13] (G-normal distribution) A d-dimensional random vector ![]() on a sublinear expectation space
on a sublinear expectation space ![]() is called (centralized) G-normal distributed if
is called (centralized) G-normal distributed if
![]()
where ![]() is an independent copy of X.
is an independent copy of X.
Now we give the definition of G-Brownian motion, G-quadratic variation process, and multi-dimensional G-Itô formula.
Definition 3 [13] A d-dimensional process ![]() on a sublinear expectation space
on a sublinear expectation space ![]() is called a G-Brownian motion if the following properties are satisfied:
is called a G-Brownian motion if the following properties are satisfied:
1)![]() ;
;
2) For each![]() , the increment
, the increment ![]() is
is ![]() -distributed and is independent from
-distributed and is independent from![]() , for each
, for each ![]() and
and![]() .
.
Definition 4 [13] Let ![]() be a d-dimensional G-Brownian motion. For each fixed
be a d-dimensional G-Brownian motion. For each fixed![]() ,
, ![]() is a 1-dimensional Ga-Brownian motion. We can define
is a 1-dimensional Ga-Brownian motion. We can define
![]()
where ![]() is called the quadratic variation process of
is called the quadratic variation process of![]() .
.
Definition 5 [13] Let ![]() with
with ![]() satisfying polynomial growth condition for
satisfying polynomial growth condition for![]() , and
, and ![]() satisfying
satisfying
![]()
where ![]() is the i-th of
is the i-th of![]() ,
, ![]() and
and ![]() are the line i and column j elements of
are the line i and column j elements of ![]() and
and ![]() respectively. And
respectively. And ![]() be bounded processes in
be bounded processes in![]() . Then for each
. Then for each ![]() we have, in
we have, in ![]()
![]()
Lemma 1 [13] In the G-expectation space, the following product rule is established:
![]()
![]()
![]()
The definition of G-Stratonovich integral for G-Brownnian motion is as below.
Definition 6 [13] Let ![]() is G-Itô process, then the G-Stratonovich integral of
is G-Itô process, then the G-Stratonovich integral of ![]() is
is
![]()
3. Main Result
In this section, in a multi-index ![]() the components that equal 0 refer to an integration with respect to time; the components that equal
the components that equal 0 refer to an integration with respect to time; the components that equal ![]() refer to an integration with respect to Stratonovich integral. We shall denote by
refer to an integration with respect to Stratonovich integral. We shall denote by ![]() and
and ![]() the sets of functions
the sets of functions ![]() for which
for which ![]() and
and![]() , respectively, where
, respectively, where ![]() is a d-dimensional Itô process which satisfies the Stratonovich stochastic differential equation.
is a d-dimensional Itô process which satisfies the Stratonovich stochastic differential equation.
Definition 7 Let ![]() and
and ![]() be two stopping times with
be two stopping times with ![]() w.p.1. Then for a multi-index
w.p.1. Then for a multi-index ![]() and a function
and a function ![]() we define the multiple Stratonovich integral
we define the multiple Stratonovich integral ![]() recursively by
recursively by
![]() (1)
(1)
There is a recursive relationship for multiple Stratonovich integrals analogous to that for multiple Itô integrals when the integrand is identically equal to 1. In order to state it succinctly we shall use the abbreviation
![]()
and as before, write ![]() for
for![]() . Based on the above multiple Stratonovich integral, we would like to consider the following special cases.
. Based on the above multiple Stratonovich integral, we would like to consider the following special cases.
Theorem 1 When![]() , the multiple G-Stratonovich integral and Hermite polynomials have the following relations
, the multiple G-Stratonovich integral and Hermite polynomials have the following relations
![]() (2)
(2)
where![]() .
.
Proof 1 For![]() , using Definition 7 and G-Itô formula we get
, using Definition 7 and G-Itô formula we get
![]() (3)
(3)
For![]() , combining with formula (3), it’s easy to get
, combining with formula (3), it’s easy to get
![]() (4)
(4)
By G-Itô formula, we have ![]() Thus the first term of the right side of formula (4) can be represented as
Thus the first term of the right side of formula (4) can be represented as
![]() (5)
(5)
We can derive
![]() (6)
(6)
Assuming that when![]() , we have
, we have
![]() (7)
(7)
It is proved that when![]() , we have the following equation
, we have the following equation
![]() (8)
(8)
Actually, applying Definition 8 and formula (7), we can get
![]() (9)
(9)
Applying G-Itô formula to ![]() and
and![]() , we have
, we have
![]() (10)
(10)
and
![]() (11)
(11)
The formula (11) is equal to
![]() (12)
(12)
Embedding formula (10) and formula (12) into formula (9), one has
![]() (13)
(13)
The proof is completed.
The next Theorem, gives a clear indication of the same structure offered by multiple Stratonovich integrals when compared with its counterpart for multiple G-Itô integrals. Similarly, we will give the proof process.
Theorem 2 For different![]() , the set
, the set ![]() being the all of the n level arrangement of
being the all of the n level arrangement of![]() , we have
, we have
![]()
such that
![]() (14)
(14)
Proof 2 For![]() , using Theorem 1 and Definition 7 we have
, using Theorem 1 and Definition 7 we have
![]() (15)
(15)
Suppose that when![]() , one has
, one has
![]() (16)
(16)
Now we prove that when![]() ,
,
![]() (17)
(17)
In fact, we only need to prove that
![]() (18)
(18)
where ![]() is
is ![]() gets rid of its last index element
gets rid of its last index element ![]() and gets the k-weight index. Using G-Itô formula and independence of G-Brownian motion on formula (18) we can get
and gets the k-weight index. Using G-Itô formula and independence of G-Brownian motion on formula (18) we can get
![]() (19)
(19)
Taking integral about the above equation, and combined with formula (18), the proof is completed.