Crystal Growth of Cu6(Ge,Si)6O18·6H2O and Assignment of UV-VIS Spectra in Comparison to Dehydrated Dioptase and Selected Cu(II) Oxo-Compounds Including Cuprates ()
UV-VIS Spectroscopy, EPR, Color, d-d Excitations, Bond Strength,
Super-Exchange Interaction
1. Introduction
Low-dimensional quantum spin systems are of considerable theoretical and experimental interests together with some applications to which they may lead. In spite of the ability of the d9 transition metal ion Cu2+ to form, apart from 3D networks, chains, ladders and small clusters, copper compounds are among the most interesting phases. With equal electronegativity compared to silicon, but in contrast to its tetrahedral networks, Cu(II) mainly forms oxo-compounds with chains and networks of connected “octahedra”.
For instance, copper polygermanate, CuGeO3, has a rather simple crystal structure of “einer” single chains of GeO4 tetrahedra alongside S = 1/2 spin single chains of edge-sharing CuO4+2 octahedra [1] [2] . It was the unique inorganic compound showing the Spin-Peierls-transition [3] [4] . As a quasi-one-dimen- sional system, it has been the subject of an intensive experimental and theoretical work for the past years. It was a great surprise, when Otto and Meibohm [5] [6] succeeded in the synthesis of pure copper polysilicate, CuSiO3, by thermal decomposition of the mineral dioptase, Cu6Si6O18・6H2O. CuSiO3 represents the example of a fully stretched silicate chain structure. It is isotypic to CuGeO3, but does not show the spin-Peierls transition, instead an antiferromagnetic ordering below TN = 7.9 K [7] [8] .
The rhombohedral title compound Cu6(Ge,Si)6O18・6H2O represents a hexacyclo-germanate (silicate) that contains copper-oxygen spiral chains along the c-axis, which are connected (intra-chain) by edge-sharing dimers (Figure 1).
![]()
Figure 1. Crystal structure of dioptase projected down [001]. A framework of copper oxide octahedra (yellow) screws around the c-axis with non-bonding axial water ligands (red) pointing towards empty channels. Six-membered silicate single rings are depicted in green.
This structure is interesting because it allows for a quantum phase transition between an anti-ferromagnetically ordered state and a quantum spin liquid [9] . Large quantum fluctuations in green dioptase have been described [10] . Recently, also the germanate analogue, Cu6Ge6O18・6H2O [11] , has been the object of detailed magnetic and structural investigations [12] [13] .
If near the empty structural channels located water molecules are removed, a screwed framework of edge-sharing disphenoids rather than flat CuO4 plaquettes remains in the dehydrated compound.
As part of a systematic study of transition metal germanates, silicates and arsenates we have undertaken syntheses of rare copper minerals and new copper compounds in view of its power as low dimensional S = 1/2 spin compounds allowing for interesting physical and physicochemical properties. First, the synthesis serves not to waste rare mineral specimens for research. There is also the possibility to study an improvement in the crystal growth by replacement of copper by other elements, apart from the chance of doping with electronically or magnetically interesting ones. For example, the replacement of copper by manganese was observed in natural samples of dioptase by EPR measurements [14] [15] .
Because the assignment of the dd excitations derived from the UV-VIS spectra of copper-bearing compounds are often found to be incorrect, this work contributed some simple tools that could lead to the right assignment. It is not the intent of this paper to review UV-VIS spectroscopy of Cu2+ compounds in general.
2. Experimental
2.1. Crystal Growth and Dehydration of the Samples
The method described below was used by the author many years earlier for the synthesis of rare minerals, for instance, the synthesis of Pb3Ge(OH)6(SO4)2・3H2O, the piezoelectric Tsumeb mineral fleischerite [16] . For the synthesis of the title compound freshly precipitated gels of GeO2 and Cu(OH)2 were separately filled in 200 ml beaker glasses and thoroughly filled up with distilled water. Then a U-shaped glass pipe of 6 mm inner diameter, well annealed before use to reduce crystal nucleation frequency, was filled free of air bubbles with distilled water. This pipe is then used to connect the distinct solutions in the beakers. Finally, the water surface in the beakers is covered with a film of liquid paraffin to prevent water evaporation and entry of CO2, respectively.
The desired slow diffusion of the distinct solutions into one another leads to the formation of Cu6(Ge,Si)6O18・6H2O seeds that grow up to 1 mm size of light blue crystals within 8 weeks. Interestingly, most individual crystals form double- crystals. The symmetry situation of this finding must be investigated further. The crystals of stocky prismatic, nearly spherical habit developed {110} and {021} forms (Figure 2).
One can extrapolate the time scale to get a crystal of about 2 mm diameter and calculate about 1 year of growing time. Trying to exchange Ge by Si by this method
![]()
Figure 2. The stocky prismatic habit of the as-grown Cu6(Ge,Si)6O18・6H2O crystals, showing a combination of the {110} prism and the {021} rhombohedron.
seems to be less efficient, only a slightly greenish sheen shows that a small exchange occurred.
The other method of co-precipitation of GeO2, SiO2 and Cu(OH)2 gel and longer time vigorous stirring resulted in a vivid green colored polycrystalline material of about 12 at-% Si determined from lattice parameter changes [14] [17] . Also, the substitution of some B3+ for Ge4+ is possible, leading to a beautiful green color [17] . Stirring a longer period and in addition changing the pH to more acidic milieu gives at least about 15 at-% Si (a = 14.640 Å, c = 7.806 Å, this work). The effect is based on the different solubility of the Ge-compound in comparison to dioptase. Cu6Ge6O18・6H2O is easily decomposed by a dilute acetic acid, but dioptase does not dissolve. Recently we observed a deepening of color to dioptase green, when the Si-rich solution was exposed to ultrasonic waves, in this way superseding vigorous stirring. The energy that is released when voids implodes (super-cavitation) may be able to assemble more easily and faster the six-membered silicate rings within the cuprate framework of dioptase.
A proposed approach for a possible synthesis of pure polycrystalline dioptase results as follows. The first step will be the spontaneous formation of pure germanate and exchange of maximum Ge by Si through stirring or sonochemical treatment. Then pH, as well as temperature, is altered to increase the solubility of the still Ge-rich compound combined with a simultaneous offer of more Si to form a dioptase layer. A new core of silico-germanate can be grown epitaxially and subsequently transformed to dioptase. Repetition of this process may finally form pure dioptase in mm-sized crystals. An automated process would make sense. Nature has similar tools in the quiver such as rhythmic property changes (concentration, pH, temperature) of metal bearing ascending or descending solutions, apart from a lot of time.
A single-phase crystalline powder of synthetic Ge-dioptase for the UV-VIS spectroscopic investigation is best obtained from an aqueous solution of pH 5.5 at room temperature, formed by mixing and stirring equal amounts of 0.02 M cupric acetate with freshly produced 0.02 M GeO2 solution. The initially formed gel settles as fully crystalline precipitate after an induction period of two days [10] .
Complete dehydration of synthetic Ge-dioptase was performed by annealing of the polycrystalline sample up to 920 K for 6 h, followed by cooling down to room temperature with a moderate cooling rate of 20 K/h. The chosen annealing temperature lies about 53 K below the temperature of decomposition to the orthorhombic spin-Peierls phase CuGeO3 [10] .
A natural dioptase samples from the locality Altyn Tyube, Kazakhstan, was used as pure silicate sample. Its complete dehydration to “black” dioptase occurs at 660 K and should be controlled by X-ray powder diffraction analysis because decomposition into CuO (tenorite) and SiO2 (partly quartz and cristobalite) starts only a few degrees higher at 673 K.
2.2. UV-VIS Spectroscopic Investigation
First results of UV-VIS spectroscopy on Cu6(Ge,Si)6O18・6H2O are given in the doctoral theses of my coworkers Brandt [17] and Meibohm [14] , respectively, whereas dioptase itself has been investigated earlier by different researchers [18] [19] [20] [21] .
Brandt [17] reported a color change from turquoise-green to blue on dehydration of dioptase-type copper germanate. In addition, the dehydrated compound showed thermochromic behavior on heating up to 500˚C with a reversible color change to vivid green similar to that of annealed CuGeO3. The color persists when Cu6Ge6O18 is rapidly cooled down to room temperature. A possible interpretation for this effect is according to [17] the low relaxation rate of the four oxygen ligands around copper. Remember that the equatorial coordination in dioptase is not planar but disphenoidic, and a change to a stiffer, more tetrahedral one may occur with raising the temperature.
A reinvestigation of the fully hydrated and dehydrated compounds is primarily undertaken in order to deconvolute and understand the broad UV-VIS spectrum of the synthetic color pigment litidionite, KNaCuSi4O10 [22] [23] , which shows similarity to that of dioptase.
The room temperature UV-VIS spectra of the samples were taken with the double-beam light scanning UV-2501PC CE spectrometer from Shimazu with selectable light sources (50W halogen lamp and D2 lamp). The powder sample was coated on a polished aluminum disk and measured in the reflection modus against a BaSO4 standard in the wavelength range between 190 and 900 nm with a spectral bandwidth of 0.1 nm using a 50 nm/min scan and choosing 0.5 nm intervals. From the less structured absorbance profile, recalculated from the measured reflectance, the energy bands were fitted with Gaussian profile functions. The better resolved spectra of the dehydrated compounds were fitted first and then the results used as start parameters for the broad spectra of the hydrated compounds.
2.3. EPR Data
Electron paramagnetic resonance spectroscopy (EPR) provides information about the electronic structure of transition metal ion complexes. For d1,9 systems such as Cu2+ centered complexes with no fine structure the principal values of the g-tensor of the spin Hamiltonian H = βeB・g・S, reflecting the symmetry of the ligand field, can be derived from the EPR spectrum, where B is the external magnetic field, S is the spin vector, and βe = ge・μB (Landé g-factor for the free electron, ge = 2.0023, Bohr magneton μB). In this contribution g values for dioptase, Cu6Si6O18・6H2O, determined by Reddy et al. [19] , and data measured by Meibohm [14] for synthetic Cu6Ge6O18・6H2O were used as expressed in its principal axes system.
3. Results and Discussion
The Gaussian peak analysis of the UV-VIS spectra was performed with the aid of own Turbo-Basic programs using recast software modules once developed for X-ray powder profile analysis, supplemented by a program to provide an illustration of single Gaussian peaks besides the cumulative curve. Fortunately, the spectra of the dehydrated compounds are well-resolved and their reliably fitted profile data could serve as input for the less-resolved spectra of the as-grown respectively hydrated natural compounds, thereby applying variable constraints to parameters (mainly the band width) during successive refinement cycles. Results of a Gaussian deconvolution of the UV-VIS spectra for the hydrated and dehydrated compounds, respectively, are given in Table 1 and depicted in Figures 3(a)-(d). λ(nm) and Γ(nm) represent wavelength and the full width of the excitation peaks, and the wavenumber E(cm−1) denotes the excitation energy. The
![]()
Table 1. Results of the Gaussian profile deconvolution of the UV-VIS spectra of the dioptase family.
P integrated band intensity (arbitrary units), Γ(nm) full band width at half f, E(cm−1) band energy, SPE assumed simultaneous pair excitation, ZRS less intense band observed only in the hydrated compounds around 2 eV could correspond to a Zhang-Rice singlet excitation, Eg large energy gap.
![]()
Figure 3. UV-VIS spectra of (a) dioptase; (b) dioptase dehydrated; (c) Ge-dioptase; (d) Ge-dioptase dehydrated. Measured spectra red, calculated spectra blue. A mineral sample of dioptase from Altyn Tyube, Kazakhstan was used besides synthetic Ge-dioptase.
remarkable integrated band intensity P (given in arbitrary units) is the consequence of non-zero dd transition probabilities due to the absence of symmetry elements on the Cu position with C1 site symmetry and the disphenoidic (stocky tetrahedral) oxygen environment with 4 distinct equatorial bond lengths indicating Cu3d-O2p hybridization. The relative width Γ/λ of the bands of the dehydrated compounds is about 18%, whereas that of the hydrated ones suffer additional broadening to about 23% caused by a vibronic contribution of the water molecule rings and due to assumed peak overlapping according to the below presented assignment.
The steep increase of absorption at the badly resolved high energy limit of the UV-VIS spectra has been simulated by a Gaussian curve, too, and may be interpreted as absorption edge, the large gap between valence and conduction band of isolator compounds. The gap is determined around 3.80 eV for dioptase and shifts to 3.76 eV for Ge-dioptase, respectively. It is slightly lower for the dehydrated compounds, giving 3.52 and 3.47 eV, respectively (Table 1). For comparison, Rudko [24] observed an absorption edge near 3.5 eV for the charge transfer insulator CuGeO3. The absorption structures at high energy just before the energy gap may be attributed to simultaneous ligand field transitions, involving both metal centers of the dimer at twice the monomer transition energy (SPE), because their oscillator strengths are too weak for charge transfer (CT) transitions. The position of a less intense absorption band observed only for the hydrated compounds around 2 eV (16,670 cm−1, 16,230 cm−1) would correspond to Zhang-Rice singlet excitations (ZRS), for instance, measured at this energy on CuO (tenorite) [25] and CuGeO3, respectively [26] .
The color of Cu2+ compounds with their Jahn-Teller distorted coordination polyhedra [27] is the conspicuously recognized property of this transition metal ion and is attributed to electronic excitations between its d-orbitals. The coordination polyhedron of copper in the d9 state with the unpaired electron in the x2 − y2 orbital is an elongated octahedron leading to splitting of formerly degenerated d-states. A recently found impressive example for a Jahn-Teller elongated octahedron is the new prototypic crystal structure of tetragonal CuO with a c > a rock salt structure [28] .
The transition energies ∆n (cm−1), derived from broad Gaussian-shaped absorption bands of UV-VIS spectra, are the energy differences between the
 ground state and the
ground state and the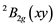 ,
, 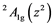 and
and 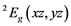 ex- cited states and can be connected with crystal field splitting parameters repre- senting orbital energies. Bearing in mind the Cu2+ site symmetry of D4h or lower, we are faced with an equatorial Dqe splitting parameter and two radial Ds and Dt ones (Gerloch and Slade, [29] ). The crystal field theory (CFT) allows for the following relations:
ex- cited states and can be connected with crystal field splitting parameters repre- senting orbital energies. Bearing in mind the Cu2+ site symmetry of D4h or lower, we are faced with an equatorial Dqe splitting parameter and two radial Ds and Dt ones (Gerloch and Slade, [29] ). The crystal field theory (CFT) allows for the following relations:
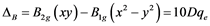 (1)
(1)
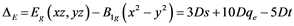 (2)
(2)
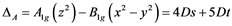 (3)
(3)
Conversely, the D parameters can be recalculated as
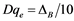 (4)
(4)
 (5)
(5)
 (6)
(6)
Whereas ∆E is always moderately larger than ∆B, ∆A ranges from about 8500 cm−1 (<∆B) for shortest axial bonds to at least 21,500 cm−1 (>∆E) for axially non- existent bonds (squared-planar coordination).
A more quantitative description of ligand field parameters using effective charges and bond lengths results in the following relations [29] :
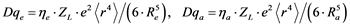 (7)
(7)
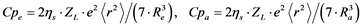 (8)
(8)
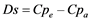 (9)
(9)
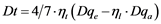 (10)
(10)
where ![]() represents an effective ligand charge, Re and Ra are equatorial and axial bond lengths in Å, and
represents an effective ligand charge, Re and Ra are equatorial and axial bond lengths in Å, and ![]() = 0.214 Å4 is the mean value of the fourth power of a 3d orbital radial distance from the nucleus, respectively
= 0.214 Å4 is the mean value of the fourth power of a 3d orbital radial distance from the nucleus, respectively ![]() = 0.294 Å2 the mean of the second power of the radial distance. For
= 0.294 Å2 the mean of the second power of the radial distance. For ![]() the values calculated by Haverkort within the Hartree-Fock approximation are used [30] . Because
the values calculated by Haverkort within the Hartree-Fock approximation are used [30] . Because ![]() is a measure proportional to the Cu(II) effective nuclear charge, one should multiply this value by a factor of 4 to give a realistic value of about 0.85 for the Scott charge, which would represent 42.5% ionicity of the Cu-O bond.
is a measure proportional to the Cu(II) effective nuclear charge, one should multiply this value by a factor of 4 to give a realistic value of about 0.85 for the Scott charge, which would represent 42.5% ionicity of the Cu-O bond.
Quoting Gerloch and Slade [29] ones more, in the crystal-field theory with its point-charge formalism charges as well as bond lengths have to be considered as effective parameters that are not independent of each other. Therefore, cationic and ligand charges should be combined to common adaptable factors ![]() respectively
respectively![]() .
.
For comparison of calculated band energies with experimental ones given in cm−1 an energy conversion factor ![]() is applied.
is applied.
Lebernegg et al. [31] found no general theoretical justification for R−5 dependence of ligand-field splitting. Nevertheless, one can use the inverse fifth power relationship Dqe µ R−5 in order to calculate a linear regression curve of Dqe (or DB) values against the mean of the four equatorial copper-oxygen distances Re(Å) according to Equation (7) for selected compounds with a reduced connectedness with respect to equatorial sharing, at the beginning excluding sheet structures as exemplified by cuprates.
The plot is depicted in Figure 4 and extrapolates well through the origin with![]() , giving effective charge numbers of Qe = ± 1.313 assumed to be evenly distributed over Cu2+ and ligands. The calculated Dqe values deviate less than 1.6% from the experimental ones.
, giving effective charge numbers of Qe = ± 1.313 assumed to be evenly distributed over Cu2+ and ligands. The calculated Dqe values deviate less than 1.6% from the experimental ones.
We chose compounds of the Egyptian Blue family (cuprorivaite, wesselite, effenbergite,) with isolated D4h plaquettes, the dehydrated dioptase compounds with equatorially edge-shared dimers, further connected via water oxygen to
![]()
Figure 4. Calculated Dq energies versus experimental ones for dioptase and related compounds. In the right plot, an additional magnetic contribution of Dqcalc for cuprates was considered.
![]()
Table 2. Coordination numbers CN, bond length and bond valence sums s for selected Cu(II) compounds. se equatorial sum, sa axial sum, Ss overall sum (particularly striking values in red).
*synthetic lammerite with an amount of CuO; **for this work a different assignment as given in the reference was used.
Recently, the energy and symmetry of dd excitations of some undoped layered cuprates have been measured by CuL3 resonant X-ray scattering [33] . The well- assigned dd excitations of these compounds with high connectedness were found to be higher than the energies of the compounds described before. Multiferroic CuO as limiting case can be added to this group with due allowance. Applying Equation (a), a steeper slope with ![]() results, representing higher excitation energies and effective charges (Qe ± 1.35) than for the dioptase group.
results, representing higher excitation energies and effective charges (Qe ± 1.35) than for the dioptase group.
The different connectedness of cuprates in comparison to the dioptase group is manifested in a larger contribution of the principal magnetic super-exchange interaction Jz to the optical excitation energies. In Figure 5, this contribution is depicted versus the Cu-O-Cu bond angle Φ, a representation first used by Rocquefelte et al. [34] , and here applied in an extended form, illustrating both dioptase group compounds and cuprate ones. A data fit resulted in the relation
![]() . (11)
. (11)
with an exponent near 5/3, explained by chemical pressure (Rocquefelte et al., 2012) [34] [35] . Adding Jz(Φ)・ln(2) as bond angle dependent contribution to the bond length dependent one, a surprisingly good agreement is achieved between the two groups of compounds, now giving![]() , respectively Qe = 1.312. It should be noticed that for the dioptase group an antiferromagnetic contribution is not included because TN is lower than room temperature, at which the optical spectra are taken.
, respectively Qe = 1.312. It should be noticed that for the dioptase group an antiferromagnetic contribution is not included because TN is lower than room temperature, at which the optical spectra are taken.
The R−5 inverse power of Cu-O bond lengths is nearly a measure for the bond strength. Therefore, the reliability of the fit can be enhanced applying the empirical Cu-O bond strength relation s = Σ(R/R0)−N [36] by choosing only the
![]()
Figure 5. Principal superexchange interaction Jz versus Cu-O-Cu bond angle Φ [34] [35] .
bond strength sum se of the four equatorial bonds. New values R0 = 1.713(9) Å, N = 5.76(16) were re-calculated for this work [37] . Results of a double-regression yielded for the cuprate group
![]() (12a)
(12a)
respectively ![]() (12b)
(12b)
for both the dioptase group and cuprates. ΔB of the last mentioned group is corrected by a bond angle dependent (magnetic) contribution (Figure 6). It is recommended to extend the analytic bond strength-bond length expression by a magnetic (angle dependent) contribution. In contrast to this result, the quoted authors [33] fitted their cuprate data with a lower slope of N = 4.2. On the other hand, the selection of compounds for such fit is not convincing, because an influence of some equatorial O− ions in La2CuO4 (high bond strength, see Table 2) on the excitation energies can be expected. In addition, the epitaxially grown infinite-layer structure of Ca0.5Sr0.5CuO2 is obviously strained.
Turning now to the calculation of splitting parameters Ds (Equation (9)) and Dt (Equation (10)) involving axial ligands one has to distinguish according to the Nephelauxetic Effect between pure oxo-ligands and such ones as H2O or Cl− with increased cationic charge and assumed higher Dqa values [29] . H2O (as equatorial ligands) are found in chalcanthite, and hydroxyl groups in azurite and conichalcite. The last compound has the most distorted “octahedron” and should show a pronounced splitting of the 2Eg term, which is not considered here.
![]()
Figure 6. A linear relation between Dq (cm−1) and the equatorial bond strength se, in case of cuprates (red curve) corrected by a bond angle dependent (magnetic) contribution to show a single linear plot (green curve) with dioptase group compounds (yellow) besides cuprates (now green).
In the case of square-planar environment it is useful to limit the extent of the ![]() orbital with “long” auxiliary axial bonds. Dehydrated dioptase and the germanate analogue already have some far distant oxygen ions (see Table 2) within the
orbital with “long” auxiliary axial bonds. Dehydrated dioptase and the germanate analogue already have some far distant oxygen ions (see Table 2) within the ![]() orbital sphere of influence. For the group of M2+CuO2 layered cuprates the limit is given by the layer separation down c of about 3.3 Å. Again the results differ somewhat for the two groups of compounds with slightly different effective charges. From the fitted values for Ds and Dt the ΔE (Equation (2)) and ΔA (Equation (3)) energies have been calculated as well as 2Eg and 2A1g. Results are summarized in Table 4.
orbital sphere of influence. For the group of M2+CuO2 layered cuprates the limit is given by the layer separation down c of about 3.3 Å. Again the results differ somewhat for the two groups of compounds with slightly different effective charges. From the fitted values for Ds and Dt the ΔE (Equation (2)) and ΔA (Equation (3)) energies have been calculated as well as 2Eg and 2A1g. Results are summarized in Table 4.
In order to check the correct assignment one can use a relation between experimental B2g, Eg and A1g values of form![]() , which results from Equations (1) to (3). Obviously, this relation holds only for shortest axial bonds and more octahedral ligand environment, such fulfilling the precondition for the underlying ionic model. For non-existent axial bonds the value for the quotient is close to unity. The values listed in Table 4 indicate clearly bond length dependence. An empirical function
, which results from Equations (1) to (3). Obviously, this relation holds only for shortest axial bonds and more octahedral ligand environment, such fulfilling the precondition for the underlying ionic model. For non-existent axial bonds the value for the quotient is close to unity. The values listed in Table 4 indicate clearly bond length dependence. An empirical function ![]() may serve as a correction giving quotients f(Δ)/f(R) near unity when using α1 = 0.59 for dioptase group compounds respectively 0.70 for cuprates. Compounds with axial water ligands or Cl− can clearly be identified by relatively small values. Another possibility here published the first time ever is to use the linear relation
may serve as a correction giving quotients f(Δ)/f(R) near unity when using α1 = 0.59 for dioptase group compounds respectively 0.70 for cuprates. Compounds with axial water ligands or Cl− can clearly be identified by relatively small values. Another possibility here published the first time ever is to use the linear relation
![]() , where
, where![]() , (13)
, (13)
with a Ra/Re ratio including well adapted auxiliary Ra bonds for compounds of coordination number 4, but different ε values for the dioptase group (![]() ) and cuprates (
) and cuprates (![]() ) to guide the regression line well through the origin (Figure 7 and Table 5).
) to guide the regression line well through the origin (Figure 7 and Table 5).
It should be stressed with respect to the use of mean bond distances in Equation (13) that also in the Equations (7) to (10) the mean of corresponding bond distances is taken first and then their inverse fifth power is calculated to yield the convincing results of Table 4.
An additional scaling ![]() between 1.7 and 2.0 (Equation (10)) is needed to fit the Dt values of compounds with H2O respectively Cl− as axial bonds. Also, La2CuO4 needs such correction (
between 1.7 and 2.0 (Equation (10)) is needed to fit the Dt values of compounds with H2O respectively Cl− as axial bonds. Also, La2CuO4 needs such correction (![]() ) possibly caused by some O- expected as axial ligands. Applied scaling factors were summarized as supplemented material in the Table 7.
) possibly caused by some O- expected as axial ligands. Applied scaling factors were summarized as supplemented material in the Table 7.
Indeed, the connectedness of copper-ligand units, representing the number of shared copper-oxygen polyhedra, should be important for the dd excitation energy. Therefore, besides the equatorial ligand sums that are calculated as fit coordinate, we used the bond valence sums to check for inconsistent structural details and signs for mixed valences. Copper polygermanate in the Pbmm prototypic structure [1] [2] shows too high a sum with Σs = 2.08. There is evidence from EPR [38] , X-ray diffraction [39] and NQR measurements [40] that copper is statistically out of center of the CuO2 plaquette, in this way the copper bond
![]()
Table 4. Comparison of experimental and calculated excitation energies and orbital ones in cm−1. ΔB is sorted from high values to low ones down the table;![]() ,
,![]() . Experimental and calculated Δ values are arranged one above the other.
. Experimental and calculated Δ values are arranged one above the other.
*) The broad band at 12,500 cm−1 is proven to split into two bands at about 10,700 cm−1 and 13,200 cm−1, respectively.
strength is reduced towards the net charge of 2+. Even large thermal displacement ellipsoids indicate structural features that require a careful evaluation. Bond lengths should be corrected for “thermal” displacement because not less than their inverse fifth power is used in calculations (see for instance [51] ).
4. EPR Analysis
Finally, the assignment of the dd excitations can be compared with results of EPR measurements. For 3d9 ions in (nearly) tetragonal ligand symmetry one can apply the following two formulas for the principal components g|| and g﬩, if the ground state is 2B1g:
![]() , (14)
, (14)
![]()
Figure 7. ΔA excitation energies (cm−1) depicted versus a function of axial to equatorial bond distances. Again the cuprate group excitations (in red) must be corrected by a (magnetic) contribution to reliably represent all data in a single regression line. Auxiliary axial bonds (see the yellow field) were introduced in case of compounds with really missing axial bonds (coordination number 4).
![]() , (15)
, (15)
where ge = 2.0023 is the g-value for the free electron, and λ is the spin-orbital coupling parameter, which yields for the free Cu2+ ion λo = 829 cm−1 [60] .
The k values are the spin orbital reduction factors used to scale the coupling parameters to the free Cu2+ ion value, k = λ/λo. This parameter reduction is attributed to covalence effects. Table 6 compares the results for dioptase and Ge- dioptase, respectively. Not surprisingly, the found covalence reduction effect is markedly smaller for the copper germanate than for the copper silicate, in accordance with crystal-chemical experience, confirming higher ionicity of the germanate (Table 6). Unfortunately, EPR data for the dehydrated compounds were not available.
![]()
Table 6. EPR analysis of dioptase related compounds.
5. Conclusion
As shown, a comparative reappraisal of Cu2+ UV-VIS spectra benefits from a special consideration of crystal-chemically similar groups of compounds, com- paring exemplarily the dioptase group, covering minerals as well as synthetic samples, with cuprates. The assignment of dd excitations and their representa- tion each on a single curve is possible by attributing a magnetic (bond angle de- pendent) contribution to the cuprate group. It is recommended to extend the bond strength-bond length relation by a bond angle dependent (magnetic) con- tribution. Deviations of the linear representation of orbital excitation energies may be helpful to discriminate results of compounds with peculiar orbital features from those with normal behavior. Fortunately, the first done assignment of well-resolved spectra of dehydrated dioptase Cu6(Ge,Si)6O18 served as input data to deconvolute the badly resolved spectra of as-grown Cu6(Ge,Si)6O18・6H2O samples. At present, the deconvolution of superposed spectra resulting from different Cu sites of a structure is inadequate. However, a pre-calculation of the expected energy levels can serve as input for fitting the experimental spectra. This has been successfully applied to lammerite. It is recommended to take a series of UV-VIS spectra step by step over the entire temperature range from hydrated to fully dehydrated dioptase as a didactic tool to follow the energy levels and their correct assignment, thereby simultaneously controlling the crystal water content by IR spectroscopy with a device that offers both analytical possibilities. Especially it should be investigated whether a Zhang-Rice excitation like that observed for CuGeO3 can be confirmed for the hydrated compounds of the dioptase family, too. In addition, the proposed assignment of the dd excitations of the green phase YBa2CuO5 should be supported by a CuL3 resonant X-ray scattering investigation.
Acknowledgements
The author would like to thank colleague Prof. Bernd Lehmann for supporting this work by the donation of wonderful dioptase pieces from Altyn-Tyube, Kazakhstan. Also my teacher, the late Prof. Hugo Strunz, donated dioptase pieces from the Tsumeb mine, Namibia.
Conflict of Interest
The author declares no conflict of interest.
Supplemented Material
![]()
Table 7. Comparison of scaling factors used for Cuprates in comparison to dioptase group compounds.