Performance Analysis of CSMA in Cognitive Radio Network with Random Residence Time of SUs ()
1. Introduction
Advances in wireless communication systems and development of new services have significantly increased the demand for more frequency bands. Cognitive radio network is one of the methods to solve the contradiction between supply and demand of the spectrum. Cognitive radio improves the spectrum efficiencies by enabling SUs to opportunistically access the channels unused by PUs.
There have been many studies on the opportunistic spectrum access for cognitive radio network. We classify the opportunistic spectrum access as the centralized (e.g., [1] [2] [3] [4]) and decentralized (e.g., [5]-[12]) cognitive medium access control (MAC) protocols. The decentralized cognitive MAC protocols can be further classified as slotted structure (e.g., [5] [6] [7] [8]) and unslotted structure (e. g., [9] [10] [11] [12]). Shunfu Jin et al. [5] analyzed the performance of the novel centralized spectrum allocation scheme in cognitive radio networks. S. Huang et al. [9] proposed three random access schemes for SUs, namely, VX, VAC, and KS schemes, with different sensing, transmission, and back-off mechanisms. D. B. Zhu et al. [10] proposed and analyzed the performance of the random m-sensing scheme in unslotted cognitive radio network based on the VAC scheme. [11] investigated the performance of CSMA in an unslotted cognitive radio Network with licensed channels and unlicensed channels. H. Q. Fang et al. [12] proposed and analyzed the performance of the grouped sensing scheme in unslotted cognitive radio network. These literatures all assume that the number of SU in the network is fixed. But in practical situation, the number of SU is not fixed because of the random mobility of SUs. SUs in the network may stay current network for continue its service or leave the current network for better service at any time. This is the motivation of our work.
In this paper, we consider CSMA with random residence time of SUs, where the SUs in the network may try to continue their services after random amount of time or leave the system forever after random residence time. We investigate the effect of random mobility of SUs on the system performance of an unslotted cognitive radio network. We analyze the system by CTMC with a level dependent QBD structure and obtain the steady state probability of the system using matrix analytic method.
The rest of this paper is organized as follows: In Section 2, the operation of all sensing scheme with random residence time of SUs is described in details. In Section 3, we analyze the performance of the system by using matrix analytic method. Numerical examples are presented in Section 4 and conclusions are given in Section 5.
2. System Model
We consider an unslotted CSMA in multi-channel cognitive radio network with M channels. The PU’s usage pattern of a channel follows On/Off process and is independent with other channel usage patterns. We define that the channel is on-period if it is used by PUs, and off-period otherwise. We assume that each SU performs perfect sensing and the sensing period of the channel is negligible and the SUs can opportunistically use the off-period of channels. It is assumed that the On-periods and Off-periods on the channel have exponential distribution with mean α−1 and β−1 respectively. We assume that SUs arrive according to Poisson processes with rate λ and the transmission times of messages for SUs are exponentially distributed with mean μ−1 (See Figure 1).
A SU always senses the channels before each message transmission. If there are idle channels, the SU occupies one of those idle channels and transmits a message and leaves the system after its transmission. When the arriving SU does not find idle channels, the SU either enters the back-off group with probability q for later retrial or give up its service and leaves the system with probability 1 − q.
When a SU is preempted by a PU, the SU performs spectrum handoff to a
channel. Spectrum handoff procedures aim to help SUs find another idle channel to send its message. If the preempted SU finds idle channels, the SU handoffs to one of those idle channels, otherwise the SU either enters the back-off group with probability q or leaves the system with probability 1 − q.
By the random mobility SUs’, the SUs in the back-off group either retry to the system in order to transmit their messages or leave the system after random residence time. The retrial time of SUs is defined as the amount of time between two consecutive retrials made by a SU and is assumed to be independent of all previous retrial times. We assume that the retrial time and residence time of SUs are exponentially distributed with mean 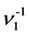 and
and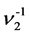 , respectively. When a SU in the back-off group retries to the system, the SU repeats the same procedure as an arriving SU does.
, respectively. When a SU in the back-off group retries to the system, the SU repeats the same procedure as an arriving SU does.
3. Performance Analysis of the System
Let
Nb(t) = the number of SUs in back-off group at time t;
Np(t) = the number of PUs in service at time t;
Ns(t) = the number of SUs in service at time t.
Then {(Nb(t), Np(t), Ns(t)) |t ≥ 0} forms 3-dimensional Markov process with state space
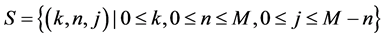
Let the elements of S be ordered lexicographically. The infinitesimal generator Q of the Markov process has a level dependent infinite QBD structure as follows
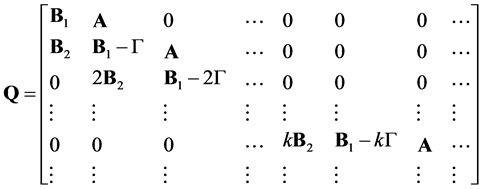 (1)
(1)
The entries of Q are given by following block matrices.
1) A is the transition rate matrix from level k to level k + 1, given by
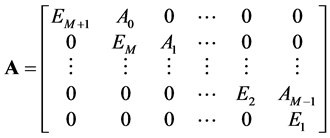 (2)
(2)
where 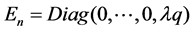 is an
is an 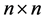 diagonal matrix and
diagonal matrix and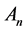 ,
, 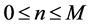 are
are  matrices as follows.
matrices as follows.
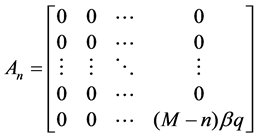
2) kB2 is the transition rate matrices from level k to level k − 1. B2 is given by
 (3)
(3)
where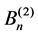 ,
, 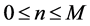 are
are  matrices and
matrices and 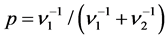 given by
given by
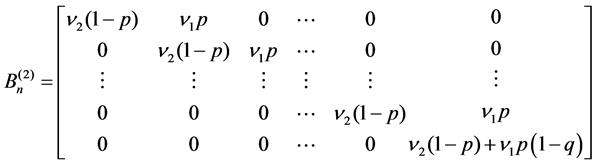
3) B1 − kΓ is the transition rate matrices in level k. The matrix Γ is given by
![]()
where
![]()
is diagonal matrix, B1 has following structure:
![]()
where Cn, ![]() are
are ![]() matrices and
matrices and![]() ,
, ![]() are
are ![]() matrices as follows:
matrices as follows:
![]()
![]()
When![]() ,
, ![]() has the structure
has the structure
![]()
where the diagonal elements bn,j are given by
1) If![]() ,
,
![]()
2) If ![]()
![]()
3) If ![]()
![]()
Note that the generator Q is a level dependent. It is obvious that the system is stable if q is less than 1. Let Π be the steady state probability vector, which is the unique solution of linear equations ΠQ = 0, Πe∞ = 1; where e∞ is an infinite dimensional column vector whose elements are all equal to 1. We partition Π as ![]() where
where![]() ,
, ![]() and
and ![]() is the probability that Markov chain is in state (k, n, j) in the steady state. We can obtain the steady state probability vector Π by matrix analytic method.
is the probability that Markov chain is in state (k, n, j) in the steady state. We can obtain the steady state probability vector Π by matrix analytic method.
The main performance measures of cognitive radio network are loss probability Pl and the throughput Ts of SUs.
Let ![]() is the probability that there are n PUs in the system and j
is the probability that there are n PUs in the system and j
SUs in service.
The loss probability Pl of SUs is defined by the ratio of the loss rate of SUs to the arrival rate of SUs. Loss of SUs occurs by the following three kinds of events:
・ a new SU is blocked and then gives up its service and thus its loss rate is given by
![]()
・ a retrial SU is blocked and then gives up its service and leaves the system after a random residence time, thus its loss rate is given by
![]()
where ![]() and
and ![]() are retrial rate and leave rate of SUs when there are k SUs in a back-off group.
are retrial rate and leave rate of SUs when there are k SUs in a back-off group.
・ a SU is preempted by a PU and then gives up its service and thus its loss rate is given by
![]()
where a SU is preempted when all M channels are busy and at least one SU occupy primary channel.
Hence the total loss rate of SUs is
![]()
Therefore the loss probability of SUs is given by
![]() (4)
(4)
The throughput Ts of SUs is defined as the number of SUs who successfully transmit their messages per unit time, i.e., we have
![]() . (5)
. (5)
4. Numerical Results
In this section, we present numerical examples to investigate the performance evaluation of CSMA in unslotted cognitive radio networks with a random residence time. We set the parameters M = 7 and the mean packet transmission time ![]() sec. Let the mean Off-periods
sec. Let the mean Off-periods![]() ,
,![]() .
.
In Figure 2, we compare the throughput of SUs versus the arrival rate of ![]() SUs in three different probability q. Figure 2(a) depicts the throughput of SUs versus the arrival rate
SUs in three different probability q. Figure 2(a) depicts the throughput of SUs versus the arrival rate ![]() of SUs. As expected, the throughput of SUs increases as the arrival rate of
of SUs. As expected, the throughput of SUs increases as the arrival rate of ![]() SUs increases. We see that the throughput of SUs in case with high probability q is larger than that in the case with low probability q, because the high probability q leads to higher channel utilization of SUs. Figure 2(b) shows the loss probability of SUs increases as the arrival rate
SUs increases. We see that the throughput of SUs in case with high probability q is larger than that in the case with low probability q, because the high probability q leads to higher channel utilization of SUs. Figure 2(b) shows the loss probability of SUs increases as the arrival rate ![]() of SUs. We also see that the loss probability of SUs in case with low probability q is larger than that in the case with high probability q.
of SUs. We also see that the loss probability of SUs in case with low probability q is larger than that in the case with high probability q.
Figure 3(a) and Figure 3(b) depict the throughput of SUs and loss probability of SUs versus the residence ![]() in three different arrival rate
in three different arrival rate ![]() of SUs. Figure 3(a) depicts the throughput of SUs versus the residence time
of SUs. Figure 3(a) depicts the throughput of SUs versus the residence time![]() . It shows that the throughput of SUs decreases as the residence time
. It shows that the throughput of SUs decreases as the residence time ![]() increases, because as the random residence time
increases, because as the random residence time ![]() of SUs increases, the number of leaving SUs will be increased to reduce the number of SUs successfully transmitted per unit of time, therefore, the throughput of the system in reducing.
of SUs increases, the number of leaving SUs will be increased to reduce the number of SUs successfully transmitted per unit of time, therefore, the throughput of the system in reducing.
Figure 3(b) shows the loss probability of SUs increases as the residence time ![]() increases. Because the high random residence time
increases. Because the high random residence time ![]() of SUs can increase the chance of SUs leave in back-off group. Therefore, as leaving the total
of SUs can increase the chance of SUs leave in back-off group. Therefore, as leaving the total
![]() (a)
(a)![]() (b)
(b)
Figure 2. Performance of SUs versus the arrival rate λ of SUs. (a) The throughput of SUs. (b) The loss probability of SUs.
number of system SUs increases, the loss probability of SUs increases.
In Figure 4, we compare the throughput of SUs and loss probability of SUs between the case with residence time and the case without residence time. Figure 4(a) shows the throughput of SUs increases as the arrival rate of ![]() SUs increases. We see that the throughput of SUs in the case without residence time is larger than that in the case with residence time. Figure 4(b) shows the loss probability of SUs increases as the arrival rate
SUs increases. We see that the throughput of SUs in the case without residence time is larger than that in the case with residence time. Figure 4(b) shows the loss probability of SUs increases as the arrival rate ![]() of SUs. We also see that the
of SUs. We also see that the
![]() (a)
(a)![]() (b)
(b)
Figure 3. Performance of SUs versus the residence time of SUs. (a) The throughput of Sus. (b) The loss probability of SUs.
loss probability of SUs in the case with residence is larger than that in the case with residence time.
Figure 2 shows the probability q leads to higher channel utilization of SUs. Figure 3 and Figure 4 show random residence characteristic of SUs has an impact on the performance of CSMA scheme in unslotted cognitive radio networks.
![]() (a)
(a)![]() (b)
(b)
Figure 4. Performance of SUs versus the arrival rate λ of SUs. (a) The throughput of SUs. (b) Performance of SUs versus the arrival rate λ of SUs.
5. Conclusion
We have considered CSMA in an unslotted cognitive radio network with random residence time and investigated the effect of random mobility of SUs. We analyze the system by CTMC with a level dependent QBD structure and obtain the steady state probability of the system using matrix analytic method, and then obtain performance measures of SU such as the loss probability of SUs and the throughput of SUs. Numerical results show that the random mobility of SUs has an impact on the loss probability and throughput of SUs in cognitive radio networks with random residence time.
Acknowledgements
This research is supported by the Science and Technology Department of Jilin province science and technology development plan project (20170520165JH), Jilin, China.