Equivalence between Modulus of Smoothness and K-Functional on Rotation Group SO(3)*

Zhuyuan Yang¹, Zongwen Yang²

¹School of Mathematics and computer Science, Yunnan Minzu University, Kunming, China.
²Department of Mathematics, Yunnan University, Kunming, China.

DOI: 10.4236/jamp.2017.52031                

Abstract

In this paper we obtain the equivalence between modulus of smoothness and K-functional on rotation group SO(3).

Keywords

Rotation Group, Modulus of Smoothness, K-Functional, Equivalence

1. Introduction

Many results of approximation are based on Euclid spaces or their compact subsets. Periodic approximation is based on compact group {exp(ix)}, whereas matrix group U(n) is the generalization of {exp(ix)}. We know homomorphism between SU(2) and rotation group SO(3), which has many applications in Physics and Chemistry. Some approximation problems on compact groups have been studied since in 1920s F. Peter and H. Weyl proved the approximation theorem on compact group, that is, the irreducible character generate a dense subspace of the space of continuous classes function. For instance, Gongsheng (see [1]) studied the basic problems of Fourier analysis on unitary and rotation groups, including the degree of convergence of Abel sum based on Poisson kernel. Xue-an Zheng (see [2] [3]) studied the polynomial approximation on compact Lie groups. D. I. Cartwright et al. studied Jackson’s theorem for compact connected Lie groups (see [4]), and so on. In this paper, we study the modulus of smoothness and K-functional on rotation group SO(3) and as classical casein Euclid space we will obtain the equivalence between them.

Let 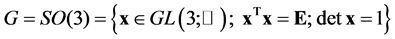be the rotation group, where 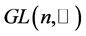is the group of invertible real (n × n) matrices. For 1 ≤ p < +∞, 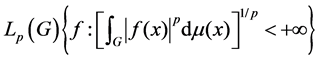, where μ is the normalized Harr measure on G. For, the Lie algebra of G = SO(3), i = 1, 2, 3, Let 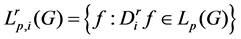, i = 1, 2, 3, where 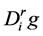denote the r-order derivative of g in direction.

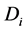We also write the difference of function f and modulus of smoothness in the direction D_i as follows

,

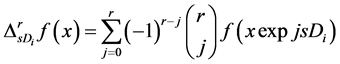and

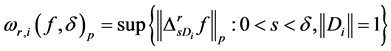
where 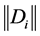is the norm induced by Killing inner product on g.

We denote

.

Accordingly, we denote K-functional as follows

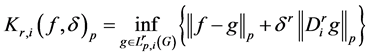
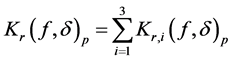
Further, for the isotropic case.

Let multi-indice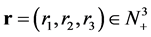, and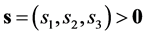, , 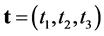, , 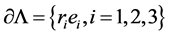here is the unit vector in the i-th direction. Define

,

and

,

and

.

The corresponding K-functional is defined by

,

where, ,.

In the next paragraph we denote by C or C_i the positive constants but are not the same in the different formula. And means there exist two positive constants C₁, C₂ satisfying C₁A ≤ B ≤ C₂A.

2. Theorems and Their Proofs

We will use the next lemma 1.

Lemma 1 [5] [6]. If, then

, where N_r denotes the normalized B-spline of order r (degree r-1).

Theorem 1. If, , , , then

.

Proof. For i = 1, 2, 3, we first construct the approximation operators as follows

By Lemma 1,

,

where.

Obviously, is a bounded operator from L_p to L_p().

If we differentiate r times, then

,

So,

. (1)

Clearly,

.

We get

,

and

.

Conversely, for, using (see [7])

,

we have

Thus

.

Theorem 2. For, , then

.

Proof. Noting that for,

,

we get

.

Writing and using the last inequality will give

.

Moreover, we construct the approximation operator as follows

where

.

It easy to see that by using the boundedness of, i = 1, 2, 3.

It is similarly to (1), we have

and.

Thus.

Remark: Theorem 1 and theorem 2 can be easily generalized to SO(n) (n > 3).

NOTES

*This research was supported by the national natural science foundation of China (11361076).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Gong, S. (1983) Harmonic Analysis on Classical Groups. Science Press, Beijing. (In Chinese).
[2]	Zheng, X.-A., Xu, Z.F. and Zhao, H.S. (987) Approximation by Polynomial on Compact Lie Groups(I). Advance in Mathematics, 16, 61-66. (In Chi-nese)
[3]	Zheng, X.-A., Zhao, H.S. and Xu, Z.F. (1990) Polynomial Approximation on Compact Lie Groups in the Lp Norm(II). Advance in Mathematics, 19, 199-203. (In Chinese).
[4]	Cartwright, D.I. and Kucharski, K. (1988) Jackson’s Theorem for Compact Connected Lie Groups. Journal of Approximation Theory, 55, 352-359. https://doi.org/10.1016/0021-9045(88)90102-5
[5]	Schumarker, L.L. (1981) Spline Functions: Basic Theory. A Wi-ley-Interscience Publication, John Wiley and Sons Inc., New York, Chichester, Brisbane, Toronto.
[6]	Dahmen, W., De Vore, R. and Scherer, K. (1980) Multi-Dimensional Spline Approximation. SIAM Journal on Numerical Analysis, 17, 380-402. https://doi.org/10.1137/0717033
[7]	Gaudry, G.I. and Pini, R. (1986) Bernstein Theorem for Compact, Connected Lie Groups. Mathematical Proceedings of the Cambridge Philosophical Society, 99, 297- 305. https://doi.org/10.1017/S0305004100064215