A Remark on the Topology at Infinity of a Polynomial Mapping F: Cⁿ→Cⁿ via Intersection Homology

Nguyen Thi Bich Thuy

UNESP, Universidade Estadual Paulista, “Júlio de Mesquita Filho”, São José do Rio Preto, Brazil.

DOI: 10.4236/apm.2016.613076                

Abstract

In [1], Guillaume and Anna Valette associate singular varieties V_F to a polynomial mapping . In the case , if the set K₀(F) of critical values of F is empty, then F is not proper if and only if the 2-dimensional homology or intersection homology (with any perversity) of V_F is not trivial. In [2], the results of [1] are generalized in the case where n≥3, with an additional condition. In this paper, we prove that for a class of non-proper generic dominant polynomial mappings, the results in [1] and [2] hold also for the case that the set K₀(F) is not empty.

Keywords

Polynomial Mappings, Intersection Homology, Singularities

1. Introduction

In [1] , Guillaume and Anna Valette provide a criteria for properness of a polynomial mapping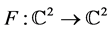. They construct a real algebraic singular variety 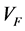satisfying the following property: if the set of critical values of 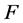is empty then 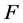is not proper if and only if the 2-dimensional homology or intersection homology (with any perversity) of 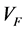is not trivial ( [1] , Theorem 3.2). This result provides a new approach for the study of the well-known Jacobian Conjecture, which is still open until today, even in the two-dimensional case (see, for example, [3] ). In [2] , the result of [1] is generalized in the general case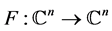, where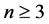, with an additional condition ( [2] , Theorem 4.5). The variety is a real algebraic singular variety of dimension in some, where, the singular set of which is contained in, where is the set of critical values and is the asymptotic set of.

This paper proves that if is a non-proper generic dominant poly- nomial mapping, then the 2-dimensional homology and intersection homology (with any perversity) of are not trivial. We prove that this result is also true for a non-proper generic dominant polynomial mapping, with the same additional condition than in [2] . To prove these results, we use the Transversality Theorem of Thom: if is non-proper generic dominant polynomial mapping, we can construct an adapted -allowable chain (in generic position) providing non triviality of homology and intersection homology of the variety, for any perversity (Theorems 5.1 and 5.2).

In order to compute the intersection homology of the variety in the case, we have to stratify the set. Furthermore, the intersection homology of the variety does not depend on the stratification if we use a locally topologically trivial stratification. It is well-known that a Whitney stratification is a Thom-Mather stratification and a Thom-Mather stratification is a locally topologically trivial stratification (see [4] [5] [6] [7] ). In order to prove the main result, we use two facts: In [6] , Thom defined a partition of the set by “constant rank”, which is a local Thom-Mather stratification; in [2] , the authors provide a Whitney stratification of the asymptotic set. One important point for the proof of the princial results of this paper is the following: we show that in general the set is not closed, so we cannot define a (global) stratification of satisfying the frontier condition. Hence, we cannot define a (global) Thom-Mather stratification of. However, we prove that the set is closed and. This fact allows us to show that there exists a Thom-Mather stratification of the set compatible with the partition of the set defined by Thom in [6] and com- patible with the Whitney stratification of the set defined in [2] (Theorem 4.6).

This paper provides also some examples to light the results. Moreover, these ex- amples provide also some topological properties of the well-known critical values set associated to a complex polynomial mapping, for instance: in general, the set is not closed; the set is not smooth; is not pure dimensional if is not dominant. Via these examples, we make clear also the well-known Thom-Mather partition of defined by Thom in [6] .

2. Preliminaries

In this section we set-up our framework. All the varieties we consider in this article are semi-algebraic.

2.1. Intersection Homology

We briefly recall the definition of intersection homology. For details, we refer to the fundamental work of M. Goresky and R. MacPherson [8] (see also [4] ).

Definition 2.1. Let be a -dimensional semi-algebraic set. A semi-algebraic stratification of is the data of a finite semi-algebraic filtration

such that for every, the set is either an emptyset or a manifold of dimension. A connected component of is called a stratum of.

Let be a stratum of and its closure in. If is the union of strata of, for all strata of, then we say that the stratification of satisfies the frontier condition.

Definition 2.2 (see [6] [9] ). Let be a variety in a smooth variety. We say that a stratification of is a Thom-Mather stratification if each stratum is a dif- ferentiable variety of class and if for each, we have:

an open neighbourhood (tubular neighbourhood) of in,

a continuous retraction of on,

a continuous function which is on the smooth part of,

such that and if, then

i) the restricted mapping is a smooth immersion,

ii) for such that, we have the following relations of com- mutation:

1)

2)

when the two members of these formulas are defined.

A Thom-Mather stratification satisfies the frontier conditions.

We denote by the open cone on the space, the cone on the empty set being a point. Observe that if is a stratified set then is stratified by the cones over the strata of and an additional -dimensional stratum (the vertex of the cone).

Definition 2.3. A stratification of is said to be locally topologically trivial if for every, , there is an open neighborhood of in, a stratified set and a semi-algebraic homeomorphism

such that maps the strata of (induced stratification) onto the strata of (product stratification).

Theorem 2.4 (see [6] [7] ). A Thom-Mather stratification is a locally topologically trivial stratification.

Definition 2.5 ( [7] ). One says that the Whitney condition is realized for a stratification if for each pair of strata and for any one has: Let be a sequence of points in with limit and let be a sequence of points in tending to, assume that the sequence of tangent spaces admits a limit for tending to (in a suitable Grassmanian manifold) and that the sequence of directions admits a limit for tending to (in the corresponding projective manifold), then.

A stratification satisfying the Whitney condition is called a Whitney stra- tification.

Theorem 2.6 ( [5] ). Every Whitney stratification is a Thom-Mather stratification, hence satisfies the topological triviality.

The definition of perversities has originally been given by Goresky and MacPherson:

Definition 2.7. A perversity is an (m + 1)-uple of integers such that and, for.

Traditionally we denote the zero perversity by, the maximal per- versity by, and the middle perversities by

(lower middle) and

(upper middle). We say that the perversities and are complementary if.

Let be a semi-algebraic variety such that admits a locally topologically trivial stratification. We say that a semi-algebraic subset is -allowable if

(2.8)

Define to be the -vector subspace of consisting in the chains such that is -allowable and is -allowable.

Definition 2.9 The intersection homology group with perversity, with real coefficients, denoted by, is the homology group of the chain complex.

Notice that, the notation refers to the intersection homology with compact supports, the notation refers to the intersection homology with closed supports. In the compact case, they coincide.

Theorem 2.10 ( [8] [10] ) The intersection homology is independent on the choice of the stratification satisfying the locally topologically trivial conditions.

The Poincaré duality holds for the intersection homology of a (singular) variety:

Theorem 2.11 (Goresky, MacPherson [8] ). For any orientable compact stratified semi-algebraic -dimensional variety, the generalized Poincaré duality holds:

where and are complementary perversities.

For the non-compact case, we have:

2.2. The Asymptotic Set

Let be a polynomial mapping. Let us denote by the set of points at which is non proper, i.e.,

(2.12)

where is the Euclidean norm of in. The set is called the asymptotic set of.

In this paper, we will use the following important theorem:

Theorem 2.13. [11] Let be a polynomial mapping. If is do- minant, i.e., , then is either an empty set or a hypersurface.

3. The Variety V_F

We recall in this section the construction of the variety and the results obtained in [1] and [2] : Let be a polynomial mapping. We consider as a real mapping. By we mean the set of critical points of. Thanks to the lemma 2.1 of [1] , there exists a covering of by semi-algebraic open subsets (in) such that on every element of this covering, the mapping induces a diffeomorphism onto its image. We may find some semi- algebraic closed subsets (in) which cover as well. By the Mosto- wski’s Separation Lemma (see [12] , p. 246), for each, there exists a Nash function, such that is positive on and negative on. We can choose the Nash functions such that tends to zero where is a sequence in tending to infinity. We define

that means, is the closure of the image of by.

The variety is a real algebraic singular variety of dimension in, with, the singular set of which is contained in, where is the set of critical values and is the asymptotic set of.

Theorem 3.1 ( [2] ). Let be a generically finite polynomial mapping with nowhere vanishing Jacobian. There exists a filtration of:

such that:

1) for any, ,

2) the corresponding stratification satisfies the Whitney condition.

Recall the condition “is nowhere vanishing Jacobian” means that the set of critical values of is an emptyset.

The following corollary comes directly from the Theorem 3.1 above.

Corollary 3.2. Let be a generically finite polynomial mapping. Then there exists a Whitney stratification of the asymptotic set.

Theorem 3.3 ( [1] ). Let be a polynomial mapping with nowhere vanishing Jacobian. The following conditions are equivalent:

1) is non proper,

2),

3) for any perversity,

4) for some perversity.

Form here, we denote by the homogeneous component of of highest degree, or the leading form of.

Theorem 3.4 [2] Let be a polynomial mapping with nowhere vanishing Jacobian. If, where is the leading form of, then the following conditions are equivalent:

1) is non proper,

2)

3) for any (or some) perversity

4), for any (or some) perversity.

Notice that with the notations (resp.), we mean the homology (resp., the intersection homology) with both compact supports and closed supports.

Remark 3.5. There exist may-be a lots of varieites associated to the same polynomial mapping, but for any variety, its properties in the Theorems 3.3 and 3.4 do not change.

The purpose of this paper is to prove that if is a non-proper generic dominant polynomial mapping, then the 2-dimensional homology and in- tersection homology (with any perversity) of are not trivial. In order to compute the intersection homology of the variety in the case, we have to stratify the set. Furthermore, the intersection homology of the variety does not depend on the stratification of if we use a locally topologically trivial stratification. By theorem 2.4, a Thom-Mather stratification is a locally topologically trivial stratification. In the following section, we provide an explicit Thom-Mather stratification of the set.

4. A Thom-Mather Stratification of the Set

We begin this section by giving an example to show that in general the set of a polynomial mapping is neither closed, nor smooth, nor pure dimen- sional. Recall that a set is pure dimensional of dimension if any point of this set admits a -dimensional neighbourhood in.

Example 4.1. Let us consider the polynomial mapping such that

Then, the jacobian determinant of is given by. If then or or. So we have the following cases:

+ if then and the axis is contained in,

+ if then and the axis is contained in,

+ if then. We observe that: if then; If then and. Moreover, since and, then, this implies. Furthermore, we have. Let

then is contained in.

So, we have (see Figure 1).

Notice that does not contain neither, nor the curve of equation in the plane. However and this is the singular point of. So, the set is neither closed, nor smooth, nor pure dimensional.

From the example 4.1, in general the set is not closed, so we cannot stratify in such a way that the stratification satisfies the frontier condition. The following proposition allows us to provide a stratification satisfying the frontier con- dition of the set.

Proposition 4.2. The set is closed. Moreover, we have

To prove this proposition, we need the three following lemmas.

Lemma 4.3. For a polynomial mapping, the set of the solutions of is closed, where is the jacobian determinant of at.

Chứng minh. Considering a sequence contained in the set such that tends to. Since is a polynomial mapping, then is also a polynomial mapping and is continuous. Hence tends to. Since for all, we have. So belongs to the set. We conclude that the set of the solutions of is closed.

Lemma 4.4. The set is contained in the set.

Proof. Let. There exists a sequence such that tends to. Then there exists a sequence contained in the set such that, for all, where is the determinant of the Jacobian

Figure 1. The set of the polynomial mapping.

matrix of. Assume that the sequence tends to and is finite. Since the set is closed, then belongs to the set. Moreover, since is a polynomial mapping, then tends to. Hence tends to and. Since is finite, then, which provides the contradiction. Then tends to infinity and belongs to.

Considering now the graph of in, that means

Let be the projective closure of in. We have the following lemma:

Lemma 4.5. The asymptotic set of a polynomial mapping is the image of the set by the canonical projection.

This lemma is well-known. In fact, this is the first observation of Jelonek [11] when he studied the geometry of the asymtotic set. We can find this fact, for example, in the introduction of [1] . We provide here a demonstration of this observation.

Proof. Firstly, we show the inclusion. Let, there exists a sequence such that tends to infinity and tends to. The limit of the sequence is, where and.

Now we show the inclusion. Let , then there exists such that but. Then we have. Moreover, there exists a sequence such that tends to. Hence the sequence tends to and tends to. Since is a polynomial mapping, then tends to. But, then, and tends to infinity. Thus we have.

We prove now the proposition 4.2.

Proof. By the lemma 4.5, the set is the image of the set by the canonical projection. Then the set is closed. Moreover, we have

By the lemma 4.4, we have, then Consequently, the set is closed.

Theorem 4.6. Let be a generically finite polynomial mapping. Let be the partition of defined by Thom in [6] and let be the stratification of defined in [2] (see Theorem 3.1 and Corollary 3.2). Then there exists a Thom-Mather stratification of the set compatible with and.

Proof. By the Proposition 4.2, we have. So, in order to define a Thom-Mather stratification of, we have to define a Thom- Mather stratification of the set.

Considering the partition of defined by Thom [6] and the stra- tification of defined in [2] . Notice that:

+ is a local Thom-Mather partition ( [6] , Theorem 4.B.1).

+ Since is a generically finite polynomial mapping, then by the Theorem 4.1 in [2] (see Theorem 3.1), is a Whitney stratification. Hence is a Thom-Mather stratification (Theorem 2.6).

We define now a partition of of, denoted by, as follows:

Since is a local Thom-Mather partition, then is a Thom-Mather strati- fication. Since a Thom-Mather stratification is a particular case of a Whitney stra- tification (Theorem 2.6), then we can use the result in [13] , we have is a Thom-Mather stratification (see Tranversal intersection of stratifications in [13] , p. 4).

Finally, we define a stratification of, denoted by, as follows:

.

By the Proposition 4.2, since is closed, then the obtained partition is a Thom-Mather stratification. It is clear that this stratification is compatible with and defined by [6] and [2] , respectively.

Remark 4.7. Another way to define a Thom-Mather stratification of the asymptotic set is to use “la méthode des façons” in [14] . In fact, the stratification of the asymptotic set defined by “la méthode des façons” is a Thom-Mather stratification (see [15] ).

The following example is for making clear the idea “define a partition of the set by constant rank” defined by Thom in [6] .

Example 4.8. Let us consider the example 4.1: let be the polynomial mapping such that.

We provide a partition of the set by “constant rank” defined by Thom in [6] of this example, consisted in the five following steps.

1) Step 1: Subdividing the singular set of into subvarieties, where. From the example 4.1, we have:

2) Step 2: Subdividing the sets in step 1 into smooth varieties. Since is not smooth, so we need to subdivide into, and.

3) Step 3: Making a partition of the set from the subsets in the steps 1 and 2. Since, so let us consider:

We get a partition of.

4) Step 4: Computing. We have

5) Step 5: Computing We have

Recall that

Each is a -dimensional smooth variety of. So we get a partition of by smooth varieties (see Figure 2).

Remark 4.9. If is smooth, then we can define easily a stratification of the set. But in general, is not smooth. We can check this fact in the following example:

.

Figure 2. The partition of defined by Thom of the polynomial mapping.

Remark 4.10. In all examples in this paper and in [16] , the set is pure dimensional if is dominant. So we can suggest the following conjecture:

Conjecture 4.11. If is a dominant polynomial mapping then the set is pure dimensional.

Notice that the above conjecture is not true in the case is not dominant, as shown in the following example:

5. The Homology and Intersection Homology of the Variety V_F

In this section, we prove the principal results of the paper, which are the two following theorems.

Theorem 5.1. Let be a non-proper generic dominant polynomial mapping. Then for any variety associated to, we have

1),

2) for any perversity,

3) for some perversity.

Theorem 5.2. Let be a non-proper generic dominant poly-

nomial mapping. If, where is the leading form of,

then for any variety associated to, we have

1)

2) for any (or some) perversity,

3), for any (or some) perversity.

Before proving these theorems, we recall some necessary definitions and lemmas.

Definition 5.3. A semi-algebraic family of sets (parametrized by) is a semi- algebraic set, the last variable being considered as parameter.

Remark 5.4. A semi-algebraic set will be considered as a family para- metrized by. We write, for “the fiber of at t”, i.e.:

Lemma 5.5 ( [1] lemma 3.1). Let be a -cycle and let be a com- pact semi-algebraic family of sets with for any. Assume that bounds a -chain in each, small enough. Then bounds a chain in.

Definition 5.6 ( [1] ). Given a subset, we define the “tangent cone at infinity”, called “contour apparent à l'infini” in [16] by:

Lemma 5.7 ( [2] lemma 4.10). Let be a polynomial mapping and be the zero locus of, where is the leading form of. If is a subset of such that is bounded, then is a subset of, where.

Proof. (Proof of the Theorem 5.1).

The proof of this theorem consists into three steps:

+ In the first step, we use the Transversality Theorem of Thom (see [17] , p. 34): if is non-proper generic dominant polynomial mapping, we can construct an adapted -allowable chain in generic position providing non triviality of homology and intersection homology of the variety, for any perversity.

+ In the second step, we use the same idea than in [1] to prove that the chain that we create in the first step cannot bound a -chain in.

+ In the third step, we provide an explicit stratification of the singular set of, so that the properties of the homology and the intersection homology of the set in the theorem do not change for all the varieties associated to.

a) Step 1: Let be a generic polynomial mapping, then ( [1] , proposition 2.3). Assume that. We claim that. In fact, since is dominant, then by the Theorem 2.11, we have. Moreover, since is generic then. Thanks again to the genericity of, we have. Let, then there exists a complex Puiseux arc in, where

(with is a negative integer, is an unit vector of and a small 2-dimensional disc centered in 0 and radius) tending to infinity in such a way that converges to. Then, the mapping, where (see the construction of the variety, Section 3) provides a singular -simplex in that we will denote by. We prove now the simplex is -allowable for any perversity. In fact, since, the condition (see 2.8)

where holds for any perversity since.

Notice that is not smooth in general. In fact,. Let us consider a stratum of the stratification of defined in the Theorem 4.6 and denote. Assume that, we can choose the Puiseux arc such that lies in the regular part of, thanks to the genericity of. In fact, this comes from the generic position of transversality. So is - allowable. Hence we only need to consider the cases and. Then:

1) If intersects: since, then we have. Considering the condition

(5.8)

We see that, for and. So the condition (5.8) holds.

2) If does not meet, then the condition

holds always.

In conclusion, the simplex is -allowable for any perversity.

We can always choose the Puiseux arc such that the support of lies in the regular part of and bounds a 2-dimensional singular chain e of. So is a -allowable cycle of.

b) Step 2: We claim that cannot bound a -chain in. Assume otherwise, i.e. assume that there is a 3-chain in, satisfying. Let

By definition 5.6, the sets and are subsets of. Observe that, in a neighborhood of infinity, coincides with the support of the Puiseux arc. The set is equal to (denoting the orbit of under the action of on,). Let be the zero locus of the leading forms. Since and are bounded, then by lemma 5.7, the sets and are subsets of.

For large enough, the sphere with center 0 and radius in is transverse to and (at regular points). Let

Then is a chain bounding the chain. Considering a semi-algebraic strong deformation retraction, where is a neighborhood of in onto. Considering as a parameter, we have the following semi- algebraic families of chains:

1), for large enough, then is contained in,

2), where,

3), we have,

4), we have.

As, near infinity, coincides with the intersection of the support of the arc with, for large enough the class of in is nonzero.

Let, consider as a parameter, and let, , as well as the corresponding semi-algebraic families of chains.

Let us denote by the closure of, and set. Since the strong deformation retraction is the identity on, we see that

Let us denote by the closure of, and set. Since bounds, then is contained in. We have

The class of in is, up to a product with a nonzero constant, equal to the generator of. Therefore, since bounds the chain, the cycle must bound a chain in as well. By Lemma 5.5, this implies that bounds a chain in which is included in.

The set is a projective variety which is an union of cones in. Since, so and. The cycle thus bounds a chain in, which is a finite union of circles, that provides a contradiction.

c) Step 3: We prove at first the afirmation: If is dominant, then is generically finite. Recall that is generically finite if there exists a subset in the target space such that is dense in and for any, the cardinality of is finite. To prove that is generically finite, we do two steps:

+ Prove that. In fact, by the definition of (see (2.12)), it is clear that. Take now, then there exists a sequence such that tends to. If tends to infinity, then belongs to. If does not tend to infinity, assume that tends to. Since is a polynomial mapping and hence is continuous, then tends to. Moreover is a Hausdorff space, then. This implies that. Consequently, we have. We conclude that.

+ Indicate that there exists a dense subset in the target space in the target space such that for any, the cardinality of is finite. In fact, let

Since is dominant, then by the Theorem 2.13, the dimension of is. Hence is dense in the the target space. With each, since, and since is a polynomial mapping, then the cardinality of is finite (see, for example, the Proposition 6 of [11] ). Then is generically finite.

Since is generically finite, then by the Theorem 4.6, there exists an explicit Thom-Mather stratification of the set, which is compatible with the Thom-Mather partition of defined by [6] and is compatible with the Whitney stratification of defined in [2] . In other words, there exists an explicit Thom- Mather stratification of the variety, since is the singular part of the set. We use this stratification to calculate the intersection homology of the variety. Since the obtained stratification is a Thom-Mather stratification, then it is a locally topologically trivial stratification (Theorem 2.6). Hence the intersection homology of the variety does not depend on the stratification of (Theorem 2.9). Con- sequently, the properties of the homology and the intersection homology of the variety in the theorem do not depend on the choice of the varieties associated to the polynomial mapping.

We prove now the Theorem 5.2.

Proof. (Proof of the Theorem 5.2).

Assume that is a non-proper generic dominant polynomial mapping. Similarly to the previous proof, we have:

・ Since is dominant, then by the Theorem 2.13, we have. Moreover, since is generic then. Thanks again to the genericity of, we have. Let, then there exists a complex Puiseux arc in, where

(with is a negative integer and is an unit vector of) tending to infinity such a way that converges to. Since and is generic, then we can choose the arc Puiseux in generic position, that means the simplex is -allowable for any perversity.

・ Now, with the same notations than the above proof, we have: Since

then. Moreover since then and. The cycle bounds a chain in, which is a finite union of circles, that provides a contradiction.

Hence, we get the facts (1) and (2) of the theorem. Moreover, from the Goresky- MacPherson Poincaré Duality Theorem (Theorem 2.11), we have

where and are complementary perversities. Since the chain that we create in the proof of the Theorem 5.1 can be either a chain with compact supports or a chain with closed supports, so we get the fact (3) of the theorem.

Remark 5.9. The properties of the homology and intersection homology in the Theorem 5.1 and 5.2 hold for both compact supports and closed supports.

Remark 5.10. From the proofs of the Theorems 5.1 and 5.2, we see that the properties of the intersection homology in these theorems do not hold if is not dominant. The reason is that the Theorem 2.11 is not true if is not dominant and then the condition (5.8) does not hold. However, the properties of the homology hold even if is not dominant. So we have the two following corollaries.

Corollary 5.11. Let be a non-proper generic polynomial mapping, then.

Corollary 5.12. Let be a non-proper generic polynomial mapping. If, where is the leading form of, then.

Remark 5.13. In the previous papers [1] and [2] , the condition “is nowhere vanishing Jacobian” (see Theorems 3.3 and 3.4) implies is dominant. Hence, the condition “is dominant” in the Theorems 5.1 and 5.2 guarantees the condition of dimension of the set (see Theorem 2.13). Moreover, we need this condition in this paper also to be free ourself from the condition, since the condition of dimension of when is dominant also guarantees the (generic) tranversal position of the -allowable chain which provides non triviality of homology and intersection homology of the variety when in Theorems 5.1 and 5.2.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Valette, A. and Valette, G. (2014) Geometry of Polynomial Mappings at Infinity via Intersection Homology. Annales-Institut Fourier, 64, 2147-2163.
[2]	Nguyen, T.B.T., Valette, A. and Valette, G. (2013) On a Singular Variety Associated to a Polynomial Mapping. Journal of Singularities, 7, 190-204.
[3]	van den Essen, A.R.P. (1997) Polynomial Automorphisms and the Jacobian Conjecture. Séminaires et Congrès, 2, 55-81. Société Mathématique de France.
[4]	Brasselet, J.-P. (2015) Introduction to Intersection Homology and Perverse Sheaves. Instituto de Matemática Pura e Aplicada, Rio de Janeiro.
[5]	Borel, A., et al. (1984) Intersection Cohomology, Progress in Mathematics Vol 50. Birkhaüser.
[6]	Thom, R. (1969) Ensembles et morphismes stratifiés. Bulletin of the American Mathematical Society, 75, 240-284. https://doi.org/10.1090/S0002-9904-1969-12138-5
[7]	Whitney, H. (1965) Tangents to an Analytic Variety. Annals of Mathematics, 81, 496-549. https://doi.org/10.2307/1970400
[8]	Goresky, M. and MacPherson, R. (1983) Intersection Homology II. Inventiones Mathematicae, 72, 77-129. https://doi.org/10.1007/BF01389130
[9]	Mather, J. (1970) Notes on Topological Stability. Miméographié, Harvard University, Cambridge, MA.
[10]	Goresky, M. and MacPherson, R. (1980) Intersection Homology Theory. Topology, 19, 135-162. https://doi.org/10.1016/0040-9383(80)90003-8
[11]	Jelonek, Z. (1993) The Set of Point at Which Polynomial Map Is Not Proper. Annales Polonici Mathematici, 58, 259-266.
[12]	Mostowski, T. (1976) Some Properties of the Ring of Nash Functions. Ann. Scuola Norm. Sup. Pisa Cl. Sci., 3, 245-266.
[13]	Trotman, D. (2005) Lectures on Real Stratification Theory. LATP-UMR 6632, University of Provence, Marseille.
[14]	Nguyen, T.B.T. (2015) La méthode des façons. ArXiv: 1407.5239.
[15]	Nguyen, T.B.T. (2016) Une stratification de Thom-Mather de l'ensemble asymptotique d'une application . ArXiv: 1611.01384.
[16]	Nguyen, T.B.T. (2013) étude de certains ensembles singuliers associés à une application polynomiale. Thèse, Université d’Aix Marseille. http://tel.archives-ouvertes.fr/
[17]	Arnold, V., Varchenko, A. and Goussein-Zadé, S. (1986) Singularités des applications différentiables. éditions Mir Moscou. (Original Edition in Russian, 1982)