1. Introduction
Brass is a metal alloy made of copper and zinc [1] , whose proportions can be varied to create a range of brasses with varying properties [2] . The formation of brass makes it a substitutional alloy i.e. atoms of the two constituents may replace each other within the same crystal structure [1] . Brass has higher malleability compared to its counterpart bronze [1] . However, both may also include small proportions of a range of other elements including arsenic, phosphorus, aluminum, manganese and silicon [1] . Generally, it has low melting point of about 900˚C to 940˚C (1652˚F to 1724˚F) depending on its composition. Its flow characteristics make it a relatively easy material to cast. By varying the proportions of copper and zinc, the mechanical properties of the brass can be changed, producing hard and soft brasses. The density of brass is approximately 0.303 lb/inch3 (8.4 grams/cm3) [3] . Cu-Zn alloy is widely used as industrial materials because of their excellent characteristics such as balance of strength, ductility, high corrosion resistance, non-magnetism and good formability [4] . Due to the excellent mechanical properties and machinability, it finds good applications in plumbing fixtures and fittings, low pressure valves, gears, bearings, decorative hardware and architectural frames [5] .
According to [1] [4] , several factors like corrosion resistance of brass to harsh environment, use in musical instrument industries, germicidal and anti-micro- bial application have contributed to increasing demands for brass alloy. In particular, electrical and electronic components’ market of high performance and multifunctional has increased, and the amount of brass alloys in these products has also enlarged [4] . On the other hand, a weight reduction of parts and product is strongly required for the energy efficiency improvement of transport equipment or miniaturization [4] . An effect of brass alloy part with a high specific gravity on the weight ratio of the total product is large [4] . It is possible to produce the small parts by using the high strength brass alloy. Thus, the weight of the product will be reduced significantly.
Today, almost 90% of all brass alloys are recycled [6] due to non-ferromag- netism. It can be separated from ferrous scrap by passing the scrap near a powerful magnet. Brass scrap is collected and transported to the foundry where it is melted and recast into billet. Billet is reheated and extruded into the desired form and size. The study is aimed at evaluating α-brass obtained from scraps Cu and Zn so as to achieve the objectives of determining the microstructure and mechanical properties of the brass as compared to normal α-brass billets.
2. General Survey on Brass Prospects
Ozgowiez et al. [7] examined the influence of the recrystallization annealing temperature on the microstructure and mechanical properties of brass Cu30%Zn subjected to cold deformation in the process of rolling at various degree of strain. The mechanical test shows that there was deterioration in the properties of the brass and an increase in the plastic properties as the recrystallization temperature was increasing within the range 400˚C - 650˚C (Table 1).
Xie et al. [8] also made a similar contributions on α-brass (Cu-38Zn-0.15Fe- 0.08Pb-0.5Ni) (mass%) by examine the effect of rotational speed during friction stir welding. With increasing rotational rates, the friction of the non-crystalliza- tion grains decreased while that of re-crystallized grains increased. The hardness
![]()
Table 1. Investigations of the mechanical properties of brass (Cu30%Zn) after cold rolling and recrystallization annealing.
Tensile Strength (Rm), Yield Point (Re), Increased Elongation (A), Necking (Z). Source: [7] .
values in the nugget zones (NZs) were lighter than those in the parent material (PM). Increasing the rotational rates did not exert a noticeable effect on the tensile and yield strength of the welds but increased the elongation.
According to the investigation by [5] on α-brass (Cu44%Zn), the experimental results on microhardness and microstructure after sand casting and heat treatment show improvement in the microstructure and yields strength of the α? brass. Another recent significant contribution by Hishashi et al., [4] was achieved by studying the microstructure and mechanical properties of Cu?40% Zn brass alloy with 0.5 mass% Cr additives and monolithic Cu-40%Zn powder produced by water atomization process. These powders were consolidated by hot extrusion at various temperatures by considering the precipitation behaviour of β-phase and Cr. The results by the comparison show higher yield strength in brass alloy with Cr than the monolithic brass at the same extruded temperature. Solid solution of chromium on the Cu-40%Zn-0.5Cr brass alloy extruded at a temperature is about twice as that of the same brass alloy extruded at a higher temperature. The strength impact of Cr solid solution was much effective compared to Cr precipitation strengthening. The grain size of extruded materials increased with increasing extrusion temperature (Figures 1-3).
![]() (a)
(a) ![]() (b) (c)
(b) (c)
Figure 1.Microstructure of brass: (a) parent material (PM); (b) thermo-mechanical affected zone (TMAZ) at 600 rpm; (c) heat affected zone (HAZ) at 600 rpm. Source: [8] .
![]() (a) (b)
(a) (b) ![]() (c) (d)
(c) (d)
Figure 2. Microstructure of nugget zone (NZ 1) of friction stirred welding brass joints at (a) 400 rpm; (b) 600 rpm; (c) 800 rpm; (d) 1000 rpm. Source: [8] .
![]() (a) (b)
(a) (b)![]() (c) (d)
(c) (d)
Figure 3. Microstructure of nugget zone 2 of friction stirred welding brass joints at (a) 400 rpm; (b) 600 rpm; (c) 800 rpm; (d) 1000 rpm. Source: [8] .
3. Experimental Procedure
The Cu and Zn metals were purchased as scraps from copper wire and zinc battery casing respectively. Five different compositions of the alloy were prepared to give Cu-5%Zn, Cu-10%Zn, Cu-15%Zn, Cu-20%Zn and Cu-30%Zn alloy respectively. The total mass for each weight percentage was weighed to 1.5 kg. The alloys were prepared by method of sand casting. The sequence of production process involved in the casting is as follows: pattern making, mould and core making, casting, demoulding, removal of runner/riser and cast cleaning (Table 2).
The furnace charge was calculated using Equation (1):
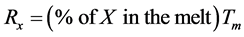 (1)
(1)
where X = constituent (Cu or Zn);
Rx = required mass of the constituent in the melt;
Tm = total mass of melt.
Parts of the cast rods were machined on a lathe to obtain the tensile test specimens. The rods were machined down to test specifications of 60 mm × 100 mm × 300 mm as shown in the Figure 4. The cast samples were subjected to homogenization annealing in order to homogenize the composition. They were heated in an OMSZON electrical furnace which was set to a temperature of 500˚C. The samples were soaked at this temperature for 3hrs and then allowed to cool slowly in the furnace. The grinding of each test sample was carried out under running water to avoid over heating of the sample with grinding machine
![]()
Figure 4. Working drawing of tensile test piece.
![]()
Table 2. Furnace charge calculation for Cu-Zn alloys.
which consist of a set of emery papers of successive grades (240, 320, 400 and 600) from coarse to finest. The subsequent grinding was done at an angle of 90˚ to the previous. In order to obtain a perfectly flat and mirror like surface suitable for metallographic examination, samples were polished using ECONET II polishing deck with emery cloth mounted on a rotating disc. Each sample was held with a gently pressure against the alumina impregnated cloth. While the process is going on, constant flow of water was maintained to wash the wear debris. The prepared polished surface of each sample was etched with ferric chloride solution for 20 seconds, and then dipped in concentrated nitric acid to remove stains. The as-received and etched samples were mounted on ACCUSCOPE metallographic microscope and examined using a magnification of ×400.
3.1. Hardness Measurement
The as-received samples and cast alloys were subjected to the hardness test using brinell hardness test accessory of the Mensanto Hounsfield Tensometer. Before the Tensometer was used, the compression attachments were mounted on the machine. After the whole setup, the corresponding Brinell hardness number was then calculated using the formula shown in the Equation (2)
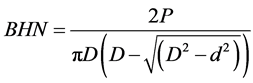 (2)
(2)
where P = applied load;
D = diameter of the indenter;
d = diameter of the impression.
3.2. Tensile Measurement
Samples from as-received and cast brass alloys that had been machined into tensile test pieces were subjected to tensile tests with the aid of a Monsanto universal testing machine. The test was carried out to determine the response of samples under the application of increasing stresses. Some properties of the alloys that were studied are as follows; yield stress, percentage elongation, reduction in area and ultimate tensile stress.
4. Results and Discussion
4.1. Hardness Test
The result of the hardness test was presented in Table 3. Also Figure 5 shows the variation in hardness of the cast Cu-Zn alloys with increasing zinc content.
![]()
Figure 5. Variation of Cu-Zn alloys with increasing zinc content.
![]()
Table 3. Results of the hardness test.
As observed in Figure 4, the hardness value of the alloys increases as the zinc content increases. In the hardness test, severe plastic flow has been concentrated in the localized region directly below the indentation, outside of which the material still behaves elastically. Directly below the indentation, the density of the particles increased locally, compared to the regions away from the depression.
Since plastic deformation in crystals is caused by the motion of dislocations, any obstacle to dislocation motion will hinder deformation and the crystal is thereby strengthened [9] . Therefore, the increase in the hardness values of the alloys with increase in zinc content is attributable to solute hardening caused by the zinc solute atoms.
4.2. Tensile Test
The result of the tensile test was presented in the Table 4. The table shows the ultimate tensile strength (UTs), yield strength, and percentage elongation (% EL) of the sample
It can be observed from Table 4, that the yield strength and ultimate tensile strength of the cast alloy samples initially increased with increase in zinc content and then decreased, with a maximum at 15 wt% Zinc. Also, the percentage elongation increased with increase in zinc content up to 20 wt% Zinc, and then decreased. Therefore, the alloy with 20 wt% Zinc has the highest ductility (Figure 6).
![]()
Figure 6. Modulus of elasticity of the alloy according to increasing zinc content.
![]()
Table 4. Tensile strength variation according to increasing zinc content.
4.3. Micrograph of the Samples
From Figures 7-12, micrographs of the various alloys reveal the presence of a single solid phase which consists of a solid solution of zinc in alpha copper. Alpha brasses containing up to 20% Zn are reddish in colour. Above 20%, the brass is yellow in colour [10] . This is expected because based on the Cu-Zn phase diagram, zinc has complete solid solubility in copper up to 35% [11] .
![]()
Figure 7. Micrograph of the as-received Cu-Zn alloy (×400).
![]()
Figure 8. Micrograph of Cu 5% Zn alloy (×400).
![]()
Figure 9. Micrograph of Cu 10% Zn alloy (×400).
![]()
Figure 10. Micrograph of Cu 15% Zn alloy (×400).
![]()
Figure 11. Micrograph of Cu 20% Zn alloy (×400).
![]()
Figure 12. Micrograph of Cu 30% Zn alloy (×400).
5. Conclusions
Hardness of the cast brass samples made from recycled copper and zinc metals increased with increase in zinc content which shows that, the higher the recycled zinc used in casting brass alloys, the harder the brass obtained.
Brass alloys made from recycled copper and zinc were seen to possess low tensile strength and ductility with increase in brittleness as the zinc content increased. This is an indication that when more zinc is added during the casting of copper alloys, for the production of brass, the brass obtained will have less tensile strength, low ductility, and high degree of brittleness.
Generally an increase in the hardness of the cast brass obtained brought about an equal decrease in the tensile strength and ductility of the metal. Thus, in order to obtain an optimum brass cast, the zinc added to the copper must be at an optimum value. Therefore, recycled copper and zinc can be applied in brass production for engineering applications.
6. Recommendations
Based on the results obtained in this work, it is therefore recommended that the hardness property of Cu-Zn alloys can be improved by addition zinc. However, further research work is required to determine other mechanical properties of the alloys (such as compression strength and impact strength) in order to obtain the optimum contents for Cu-Zn alloys which give the best combination of mechanical properties.