Sample Selection Model with Bootstrap (BPSSM) Approach: Case Study of the Malaysian Population and Family Survey ()
1. Introduction
Sample selection model is part of the field of econometrics. The term “selection” or “select” is the term commonly used and it is mentioned in a number of different issues related with the econometric data. Sample selection was developed [1] . This model also has good interaction of relation and ideal to expert evaluation and quantitative information.
The earliest introduced model consists of female labour force and wage equality [2] , [3] . They have used this model widely in the model affects unions, occupational choices, schooling choices, options and also a residential area of the industry. According to [4] in the female labour supply model, the binary model choice whether a person’s functioning and conditions of work can be seen in working hours. Traditionally, this model has been estimated by maximum likelihood or using computerized methods called Heckman two-step method.
Model selection consists of two parts [5] . The first part is the selection equation (known as the participation or equality of results). In this section, not random sample taken into account for the observation of the process of entering the sample and determine a probability sample of the population. This combination can fix the not random sample and the estimated relation of the population. The second part is the structural equation. This is also known as equality of outcome or equality of salaries with relationship desired study population centres.
Therefore, to get the accurate and precise estimation, bootstrap approach was introduced. Through this method, Bootstrap approach will be hybridized with PSSM model called Bootstrap PSSM to get more accurate estimator result. The best model is the model contains of consistent and efficient.
Bootstrap introduced by [6] . Bootstrap is a common technique that builds confidence interval by resampling with replacement sample from finite. The main objective of this article, we propose to develop a sample selection model (PSSM) based on bootstrap approach to achieve estimation result that is more precise. After that, the model of BPSSM was applied for the Family and Population Data 1994.
2. Methods
Bootstrapping the Base Model of BPSSM
In this study, a mean process is considered to monitor individual observations of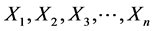 
with assumption of dependent and uncorrelated distributed. Thus, the base model and residual of BPSSM can be given by:
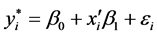
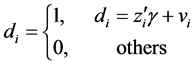
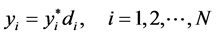(1)
where
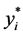and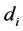 
= dependent variables
x and z = vectors of exogenous remaining variables
, 
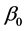and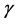 
= unknown parameter vectors
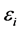and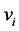 
= zero mean error terms
The standard approach is to assume that follow a bivarite normal distribution and then applied to the maximum likelihood estimation or a two-stage estimation procedure purposed by Heckman (1979). Firstly, how to estimate 
and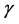 
consistently from the data. In general, both the error terms are correlated, since that the regression of y on x for the selected sample will not give consistent estimates of
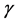. It is well known that the consistency of those estimators depends on the assumption of bivariate normality. For a random sample from the population it is observed that 
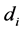x and z. If and only if, observation of 
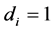then, we observed
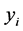. This sample selection models in (1) consist of two equations or parts; the first structural part, embodying the desired population relationship or is the equation of primary interest and second, the selection part or is the reduced form takes account of the non-representative nature of the present non-random sample. From the literature (Martin, 2001), the identification purpose, the variable z contains at least one variable which does not appear the relation between an outcome in interest y and a vector of covariates x and the selection equation describing the relation between a binary participation decision 
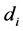and another vector of covariates z.
In this study, the hybridization of bootstrap approach in base model (1). This hybridization produced a hybrid control charts where the basic model named by Bootstrap PSSM (BPSSM). The algorithm for this hybrid process is as follows:
Step 1: A sample data, ![]()
generated by time ![]()
from a dependent and colerated distribution. The data then will be used to estimate parameter of![]()
, base model of PSSM ![]()
Step 2: Find bootstrap replication, B(c) by using:
![]()
where ![]()
and ![]()
defines as average of expected of error and true value of error respectively. This estimation will be repeated several times to get a constant value of bias and this new value will be used to analyze data in Step 1.
Step 3: By continue from Step 2, the residual value will be used in sampling with replacement method to get a matrix of residual bootstrap, ![]()
![]()
Step 4: For each residual in Step 3, compute new data ![]()
Step 5: Compute average of column of ![]()
by using![]()
, with c defines as summation of bootstrap replication, for example c = 1000
Step 6: By using bootstrap data, ![]()
compute parameter of ![]()
Step 7: For complete PSSM model, ![]()
must be hybrid with bootstrap approach. Step 1 until Step 6 rapidly to compute bootstrap data of![]()
.
Step 8: After the both equation have bootstrap data, Heckman Two Step estimation was used base on model BPSSM;
![]()
(2)
In this study, we intend to examine the performance of BPSSM in terms of effectiveness and efficiency control. Numerical estimation was selected to be used in this study. For numerical estimation, basically it is used to examine effectiveness of base model where is evident in two kind of methods, i.e. confidence interval, bootstrap percentile (PB) and Biased Corrected and Accelerate (BCa). BP and BCa selection is motivated by the advantages of these two methods in which BP is the basic method for estimating bootstrap intervals while BCa is a method that can improve BP interval estimation [7] . The main reason for selecting different methods is to finds the differences in the effectiveness of the hybrid model when using those interval methods. In theory, a model that gives the shortest interval estimation is said to be more effective model. This is because; short interval giving the idea that model estimation is closer to real interval estimation. Therefore, the lower and upper limit ![]()
can be given by:
Student’s-t:
![]()
(3)
Bootstrap Persentile (BP):
![]()
(4)
Bias Corrected and accelerated (Bca):
![]()
(5)
where ![]()
in Equation (3) represent value of percentage ![]()
for student’s-t distribution with n − 1 degree of freedom.
In this study, ![]()
is valued as ![]()
and standard error estimation, ![]()
can be calculated using the discussion on [7] .
For Equation (4), length of this interval based on percentile of mean estimation of bootstrap replication, B of ![]()
where ![]()
and ![]()
[7] . In other word, upper and lower limit of BP refers to the interval length from 50-th through 950-th replication. While ![]()
and ![]()
in Equation (5) refers to normal confidence interval with ![]()
and ![]()
respectively.
Mean Square Error (MSE) and Root Mean Square Error (RMSE) was used for error estimation in this study. In theory, a model that gives the smallest estimation value is said to be more efficient and automatically show the effectiveness of the model itself [8] . By taking the idea of small error in base model, it clearly shows that model is giving more accurate estimation. Thus, error estimation used in this study is given:
![]()
(6)
![]()
(7)
where for both MSE and RMSE refers to differences of real error, ![]()
with expected of error estimation,![]()
.
3. Results and Discussion
Application of Hybrid Model: The Malaysian Population and Family Survey 1994 Data
A comparison of performance of the real model, PSSM and hybrid model, BPSSM in terms of effectiveness or efficiency base on model estimation. The data set used for this study is from the Malaysian population and family survey 1994 (MPFS-1994). This survey was conducted by National Population and Family Development Board of Malaysia under Ministry of Women, Family and Community Development Malaysia. This survey was specifically for married women, providing relevant and significant information for the problem of married women status regarding wages, educational attainment, household composition and other socioeconomic characteristics. The original MPFS-94 sample data comprises 4444 married women.
The whole data sets used in this study consisted of 2792 married women. The selection rules [9] were applied to create the sample criteria of choosing for participant and non-participant married women on the basis of the MPFS-94 data set, which are as follows:
・ Married and aged below 60
・ Not in school or retired
・ Husband present in 1994
・ Husband reported positive earnings for 1994
The empirical results of the basic specification one are presented for the Heckman two-step approach. These approaches consider the probit estimates for the participation equation as a first step and OLS estimates for the wage equation as the second step. We discuss both the participation and wage equation on the estimated coefficient for interval method, the significant effect, and consistency and for PSSM, as well as BPSSM for comparison purposes.
Based on Table 1, the estimate for the standard intervals (Student’s-t confidence interval) using hybrid model gives a shorter interval. See for example, the length of BPSSM-t valued 0.0512791 compare to real model, PSSM-t which is more length 1.0898210. This result can be seen clearly in Figure 1. The differences shown in these two models proved that the bootstrap approach fixed the interval estimation and gives a good performance for hybrid model.
In Figure 1 and Figure 2, a plot of interval estimation for Student’s-t method in Figure 1 and also a plot of Bootstrap Percentile (BP) and Bias Corrected and accelerated (BCa) showed in Figure 2. Based on these two plots, we found that bootstrap interval method, i.e. BP and BCa, gave short length compare to the standard interval which show a length interval either for real or hybrid model. Significant difference on the length value shows that the bootstrap percentile interval method gave a good performance compare to Student’s-t estimation. By considering this result, we can say that BPSSM model gives a better performance when using bootstrap interval method. With this result, it’s clearly proved that hybrid model provides an effective estimation compare to the real model.
![]()
Table 1. Interval estimation for the real and hybrid model.
![]()
Figure 1. Interval estimation of standard interval: Student’s-t.
![]()
Figure 2. Interval estimation of bootstrap interval method.
![]()
Table 2. Error value for real and hybrid model.
Next, estimation of the effectiveness of the real and hybrid models is seen in the results of the MSE and RMSE and the good performance of the model is based on the theory of effectiveness estimation model, as discussed in the previous section. Therefore, the results of this error can be referred to Table 2.
Based on the results of Table 2, a model with the bootstrapping approach provides the smallest error value compared to the real model, PSSM. For example, the estimation result for MSE of hybrid model is 0.019855010 while real model gives large error estimation, i.e. 0.023978510. These results are plotted in Figure 3 and Figure 4 for an illustration comparing the results for both models of MSE and RMSE estimation value.
Based on such a significant error reduction in Figure 3 and Figure 4, show the boot-
![]()
Figure 3. Plot of error estimation, MSE.
![]()
Figure 4. Plot of error estimation, RMSE.
strap approach in real base model of control charts fixing the estimation of real model and provide a more accurate estimation for the model. This small error values also indicate that the hybrid model is more effective and gives good performance compared to the real model, PSSM.
4. Conclusion
In this study, a PSSM model was hybrid with bootstrap method using an alternative algorithm. Using an alternative algorithm, the hybrid process was involved the construction of a standard error of PSSM confidence interval and proposed a new hybrid model of BPSSM. The data set Malaysian population and Family survey 1994 (MPFS-1994) was used. Participation and wage equation on the estimated coefficient for interval method, the significant effect, and consistency and for PSSM, as well as BPSSM for comparison purposes was discussed. The differences shown in these two models proved that the bootstrap approach fixed the interval estimation and gives a good performance for hybrid model. Estimation of the effectiveness of the real and hybrid models is seen of the MSE and RMSE. This small error value also indicates that the hybrid model is more effective.
Acknowledgements
A special gratitude for School of Informatics and Applied Mathematic (SIAM) and Research Management Centre (RMC), Universiti Malaysia Terengganu for supported this research paper.