A Remarkable Chord Iterative Method for Roots of Uncertain Multiplicity

I. Fried

Department of Mathematics, Boston University, Boston, MA, USA.

DOI: 10.4236/am.2016.711106                

Abstract

In this note we at first briefly review iterative methods for effectively approaching a root of an unknown multiplicity. We describe a first order, then a second order estimate for the multiplicity index m of the approached root. Next we present a second order, two-step method for iteratively nearing a root of an unknown multiplicity. Subsequently, we introduce a novel chord, or a two- step method, not requiring beforehand knowledge of the multiplicity index m of the sought root, nor requiring higher order derivatives of the equilibrium function, which is quadratically convergent for any , and then reverts to superlinear.

Keywords

Iterative Methods, Unknown Root Multiplicity, Two-Step Methods

Received 23 May 2016; accepted 8 July 2016; published 11 July 2016

1. Introduction

The multiplicity index m of root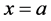, 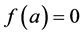of equilibrium function 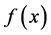may be a well latent property of the root, not cursorily revealed, nor readily available, yet this multiplicity can profoundly affect the behavior of the iterative approach [1] - [3] to the root. In this note, we briefly review the iterative methods [4] - [8] for approaching a root of an unknown multiplicity, and present a first oder [9] as well as a second order estimate for the multiplicity index m of the approached root. Then we present a novel chord, or a two-step method, not requiring beforehand knowledge of m, nor requiring the higher derivatives of the equilibrium function, which is quadratically convergent for any, and then reverts to superlinear.

2. Assumed Nature of the Equilibrium Function

We assume that near root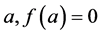, function 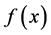has the power series representation

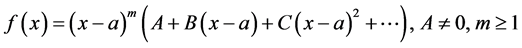(1)

where m is the multiplicity index of root a, and where etc. are, for, the coefficients

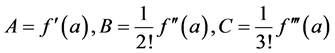(2)

and so on.

3. The Newton-Raphson Method

The Newton-Raphson method

(3)

is quadratic

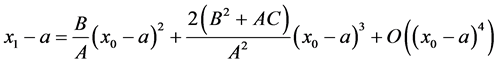(4)

if. However, if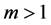, the method declines to mere linear

(5)

See also [10] .

4. Extrapolation to the Limit

Let be already near root a. Then, if

(6)

nearly. Eliminating from the two equations we obtain

(7)

which we solve for an approximate a, as

(8)

where

(9)

The square root in Equation (8) may be approximated as

(10)

and for this extrapolated of Equation (8) we have

(11)

For example, for, and starting with, we compute,; and then from Equation (8),. Another such cycle starting with produces a next.

5. Always Quadratic Newton-Raphson Method

The modified Newton-Raphson method

(12)

converges quadratically to a root of any multiplicity m

(13)

But for this we need to know m.

By Equation (1) we readily deduce that, for any x

(14)

obtained at the price of a second derivative. For finite-difference approximations of the needed derivatives see [11] - [13] . Using in Equation (14) for m in Equation (12) we obtain the method

(15)

which is quadratic for any, provided, m

(16)

The method of Equation (15) is also obtained by applying Newton’s method not to f, but rather to. For, we obtain by the method of Equation (15) that requires not only but also, starting with.

For

(17a)

For

(17b)

Equation (15) may be written as

(18)

and it is of interest to know that

(19)

For the price of a third derivative we may have the quadratic approximation

(20)

6. An Erroneous m

The method

(21)

produces the superlinear

(22)

and if, convergence is alternating.

7. Estimation of the Leading Term

We readily have that

(23)

For example, for, we compute using Equation (23) the approximations as depending on the chosen x

(24)

8. An Elementary Discrete Two-Step Newton Method for Roots of Any Multiplicity

If

(25)

are already close to root a of multiplicity, then according to Equation (5)

(26)

nearly, from which we extract the approximation

(27)

Setting a back into Equation (26) yields

(28)

and the two-step method

(29)

where in Equation (28) is seen to be but the finite-difference approximation of in Equation (14).

For example, for, and starting with, we compute by Equation (29), the successive approximations

(30a)

(30b)

(30c)

(30d)

Generally, starting with

(31)

we have from the method of Equation (29) that

(32)

The repeated classical Newton’s method, , we recall, is only linear if

(33)

See also [14] [15] .

9. Derivation of the Chord Method

It is a rational two step method of the form

(34)

With

(35)

the method is quadratic for and. In fact;

For

(36a)

For

(36b)

For

(36c)

For the method produces

(37)

and for the method is quadratic for as well.

According to Equation (36a), if, then the method is higher than quadratic.

10. The Method is Further Superlinear

For we have:

For

(38a)

For

(38b)

For

(38c)

For

(38d)

For

(38e)

For

(38f)

For

(38g)

For

(38h)

For

(38k)

For

(38l)

11. Lowering the Value of k

We leave k in of Equation (34), free, and have by power series expansion, for multiplicity index, for in Equation (1), that

(39)

The linear term in the above expansion is annulled with

(40)

We do this for higher values of m and find that

(41)

We try, and get

For

(42a)

For

(42b)

For

(42c)

For

(42d)

For

(42e)

For

(42f)

For

(42g)

For

(42h)

For

(42k)

For

(42l)

For

(42m)

The general form of the linear part of in Equations (42) is of the form with a constant that is small if multiplicity index m is not much above 5. For instance, , meaning that at each iteration the error is reduced by this factor. Such convergence behavior we term superlinear. More concretely, for, we obtain by the above method, using, starting with.

For

(43a)

For

(43b)

For

(43c)

12. Conclusions

The paper is predicated on the realistic assumption that the multiplicity index m of the iteratively targeted root is unknown. We conclude that if one prefers to shun second order derivatives, then the quadratic two-step method of Equation (29), that provides also ever better approximations for the multiplicity index m of the approached root, is a practically appealing alternative.

Otherwise, one may use the rational two-step method of Equation (34) with a constant k that is only slightly less than 2. Thus stating the method becomes superlinear, albeit, of a reduced speed of convergence for highly elevated root multiplicities. For the sake of brevity, the present paper does not explore the possibility of estimating the multiplicity index m of the sought root by the method of Equation (29), then applying this estimate to the choice of an optimal k in the method of Equations (34) and (35).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Householder, A.S. (1970) The Numerical Treatment of a Single Nonlinear Equation. McGraw-Hill, New-York.
[2]	Traub, J.F. (1977) Iterative Methods for the Solution of Equations. Chelsea Publishing Company, New York.
[3]	Ostrowski, A. (1960) Solution of Equations and Systems of Equations. Academic Press, New York.
[4]	Hansen, E. and Patrick, M.A. (1977) Family of Root Finding Methods. Numerische Mathematik, 27, 257-269. http://dx.doi.org/10.1007/BF01396176
[5]	Petkovic, M.S., Petkovic, L.D. and Dzunic, J. (2010) Accelerating Generators of Iterative Methods for Finding Multiple Roots of Nonlinear Equations. Computers and Mathematics with Applications, 59, 2784-2793. http://dx.doi.org/10.1016/j.camwa.2010.01.048
[6]	Neta, B. and Johnson, A.N. (2008) High-Order Nonlinear Solver for Multiple Roots. Computers and Mathematics with Application, 55, 2012-2017. http://dx.doi.org/10.1016/j.camwa.2007.09.001
[7]	Fried, I. (2013) High-Order Iterative Bracketing Methods. International Journal for Numerical Methods in Engineering, 94, 708-714. http://dx.doi.org/10.1002/nme.4467
[8]	King, R.F. (1977) A Secant Method for Multiple Roots. BIT, 17, 321-328. http://dx.doi.org/10.1007/BF01932152
[9]	Lagouanelle, J.L. (1966) Sur Une Metode de Calcul de l’Ordre de Multiplicite des Zeros d’Un Polynome. Comptes Rendus de l'Académie des Sciences, 262, 626-627.
[10]	Rall, L.B. (1966) Convergence of the Newton Process to Multiple Solutions. Numerische Mathematik, 9, 23-37. http://dx.doi.org/10.1007/BF02165226
[11]	Soleymani, F. (2012) Optimized Steffensen-Type Methods with Eighth-Order Convergence and High Efficiency Index. International Journal of Mathematics and Mathematical Sciences, 2012, 1-18. http://dx.doi.org/10.1155/2012/932420
[12]	Sharma, J.R. (2005) A Composite Third Order Newton-Steffensen Method for Solving Nonlinear Equations. Applied Mathematics and Computation, 169, 242-246. http://dx.doi.org/10.1016/j.amc.2004.10.040
[13]	Esser, H. (1975) Eine Stets Quadratisch Konvergente Modifikation des Steffensen Verfahrens. Computing, 14, 367-369. http://dx.doi.org/10.1007/BF02253547
[14]	Dong, C. (1987) A Family of Multipoint Iterative Functions for Finding Multiple Roots of Equations. International Journal of Computer Mathematics, 21, 363-367. http://dx.doi.org/10.1080/00207168708803576
[15]	Thukral, R. (2013) Introduction to Higher-Order Iterative Methods for Finding Multiple Roots of Nonlinear Equations. Journal of Mathematics, 2013, 1-3. http://dx.doi.org/10.1155/2013/404635