Received 24 February 2016; accepted 25 April 2016; published 28 April 2016

1. Introduction
1.1. Relativity Hypotheses
For a century, hypothesis of a variable time is laid down by the special theory of relativity. This hypothesis can explain many Nature observations, experiments and formulas, for example, the demonstration of the Lorentz factor. Because of such good explanations, the hypothesis of a variable time has been validated. Nevertheless, it remains some paradoxes and some predictions which are difficult to measure directly, as a reversible time, an “imaginary” time or even the time variation itself.
And in developing his ideas about the consequences of the equivalence principle between gravitational mass and inertial mass, Einstein leads to a new vision of gravitation which is to replace that of Newton: the general theory of relativity. The most important aspect is the disappearance of gravitational force concept. For Einstein, the motion of a body is not determined by strength, but by the configuration of space-time [1] . For example, relativity theory explains the deflection of light and the perihelion precession of Mercury, and predicts the gravitational waves which have been very recently detected.
But the absence of gravitational force and a variable time according to the reference frame remain concepts difficult to directly prove.
1.2. The Purpose
The question is: is it possible to explain such phenomena within another theory, i.e. using gravitational forces and a universal time? It is what we will try to do in this article.
A universal time would give in coherence with the universal time of the Quantum Mechanics.
1.3. Neo-Newtonian Hypotheses
The basis has been laid down in a previous article [2] : Lorentz factor can be demonstrated without using a variable time! It is only necessary to consider a variable inertial mass, different of the gravitational mass, and the energy of the particle linked to the inertial mass. If Newton distinguished the concepts of gravitational mass from the inertial mass [3] , he could not be envisioned a variation of the inertial mass only detected at very high velocity (let us remind in the 17th century, Huygens was only trying to estimate the light celerity [4] ). We will call these hypotheses: the neo-Newtonian mechanics. We compare them in Chart 1.
Now in this article, we will check the consequence of these hypotheses on force expression in general (which includes resultant gravitational force).
2. Net Force Demonstration
The linear momentum p is by definition the product of the mass of a body by its velocity [5] :
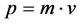 (1)
(1)
It is a general formula, the mass m is the inertial mass (it is not the gravitational mass).
So the linear momentum can be written more precisely
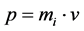 (2)
(2)
With 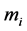 the inertial mass
the inertial mass
According to neo-Newtonian demonstration [2] , the inertial mass is linked to the gravitational mass 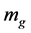 by the Lorentz factor γ
by the Lorentz factor γ
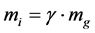 (3)
(3)
with
 (4)
(4)
Chart 1. Comparison of hypotheses.
By property of the net force F according to the second Newton’s law of motion:
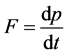 (5)
(5)
Because gravitational mass is constant:
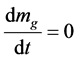 (6)
(6)
so
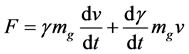 (7)
(7)
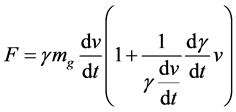 (8)
(8)
 (9)
(9)
And due to Equation (4):
 (4bis)
(4bis)
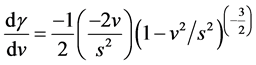 (10)
(10)
 (11)
(11)
So, with Equation (9):
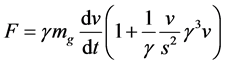 (12)
(12)
![]() (13)
(13)
And again due to Equation (4):
![]() (4ter)
(4ter)
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
And so, with Equation (13)
![]() (17)
(17)
![]() (18)
(18)
By definition, the acceleration a is:
![]() (19)
(19)
So the updated property of the net force is:
![]() (20)
(20)
3. Comments
3.1. Comparison
This expression in ![]() can look a bit strange at first sight.
can look a bit strange at first sight.
Let us remind the synchrotron radiation. The cyclotron is used for particles, and the synchrotron is used for particles at velocities close to light celerity. The loss of energy per turn by synchrotron radiation can be mea- sured as follows [6] - [8] :
![]() (21)
(21)
formula which can also be written:
![]() (21bis)
(21bis)
or
![]() (21ter)
(21ter)
And let us remind a work is a force by a length, and a length is a velocity by a time. So
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
Then, the work ![]() of a
of a ![]() force [Equation (24)] appears to be homogeneous with the measure in a synchrotron of the loss of energy W [Equation (24ter)] of particles at very high velocity. This synchrotron effect can be checked not only in a laboratory but also in pulsed emission gamma-ray radiation from pulsar [9] .
force [Equation (24)] appears to be homogeneous with the measure in a synchrotron of the loss of energy W [Equation (24ter)] of particles at very high velocity. This synchrotron effect can be checked not only in a laboratory but also in pulsed emission gamma-ray radiation from pulsar [9] .
3.2. Numerical Application
This ![]() factor can be detected only at very high velocity. At very high velocity, it is of course easier to mea- sure when the body stays close, i.e. on a constant periodic movement, as the circular motion. For example:
factor can be detected only at very high velocity. At very high velocity, it is of course easier to mea- sure when the body stays close, i.e. on a constant periodic movement, as the circular motion. For example:
・ Planet revolution (Mercury is the fastest planet of our solar system).
・ Particle in a cyclotron.
・ Particle in a synchrotron.
Let us check the value of ![]() at various velocities. See Chart 2 and/or Figure 1.
at various velocities. See Chart 2 and/or Figure 1.
It confirms
- Variation of ![]() could not envisioned at Newton’s age when the higher motion known was Mercury velocity (with a
could not envisioned at Newton’s age when the higher motion known was Mercury velocity (with a![]() ).
).
- Expression of the net force with ![]() can be checked with a synchrotron.
can be checked with a synchrotron.
3.3. Meaning
That means that, at very high velocity,
- For a same variation of velocity (or acceleration), the net force will be slightly higher than traditionally ex- pected.
Chart 2. Value of γ3 according to the velocity.
![]()
Figure 1. Value of ![]() according to the velocity.
according to the velocity.
- For a same net force, the variation of velocity (or acceleration) will be slightly lower than traditionally ex- pected and at usual velocity, ![]() , and we find back the usual formula:
, and we find back the usual formula:
![]() (25)
(25)
4. Conclusions
First, we remind results of a previous article: Lorentz factor can be demonstrated without using a variable time, but using a variable inertial mass. Such a hypothesison time, called neo-Newtonian theory, is in coherence with the Quantum Mechanics.
Then in present article, consequence of this hypothesis has been checked on net force expression. Deducted and demonstrated from the linear momentum, net force is so expressed to:![]() .
.
This ![]() factor can be detected only at very high velocity. At very high velocity, it is of course easier to mea- sure on a constant periodic movement, as the circular motion. For example, the synchrotron radiation (in synchrotron laboratory or in pulsed emission gamma-ray radiation from pulsar): the electromagnetic energy emitted by electrons or protons at circular velocity close to light celerity is done with the factor
factor can be detected only at very high velocity. At very high velocity, it is of course easier to mea- sure on a constant periodic movement, as the circular motion. For example, the synchrotron radiation (in synchrotron laboratory or in pulsed emission gamma-ray radiation from pulsar): the electromagnetic energy emitted by electrons or protons at circular velocity close to light celerity is done with the factor![]() .
.
Application of such a neo-Newtonian hypotheses on the perihelion precession of Mercury (the faster of the planets of our solar system), the deflection of light or the Doppler Effect will be done in next articles.
Acknowledgements
I would like to thank the reviewers for their advice about the looking of my article.