Kummer’s 24 Solutions of the Hypergeometric Differential Equation with the Aid of Fractional Calculus

Tohru Morita^1*, Ken-ichi Sato²

¹Tohoku University, Sendai, Japan.
²College of Engineering, Nihon University, Koriyama, Japan.

DOI: 10.4236/apm.2016.63015                

Abstract

We know that the hypergeometric function, which is a solution of the hypergeometric differential equation, is expressed in terms of the Riemann-Liouville fractional derivative (fD). The solution of the differential equation obtained by the Euler method takes the form of an integral, which is confirmed to be expressed in terms of the Riemann-Liouville fD of a function. We can rewrite this derivation such that we obtain the solution in the form of the Riemann-Liouville fD of a function. We present a derivation of Kummer’s 24 solutions of the hypergeometric differential equation by this method.

Keywords

Fractional Derivative, Hypergeometric Differential Equation, Hypergeometric Function

Received 30 November 2015; accepted 24 February 2016; published 29 February 2016

1. Introduction

The hypergeometric function is a solution of the hypergeometric differential equation, and is known to be expressed in terms of the Riemann-Liouville fractional derivative (fD) ([1] , p. 334). By the Euler method ( [2] , Section 3.2), the solution of the hypergeometric differential equation is obtained in the form of an integral, which is confirmed to be expressed in terms of the Riemann-Liouville fD of a function. This shows that we can obtain the solution in the form of the Riemann-Liouville fD of a function. In fact, Nishimoto [3] obtained a solution of the hypergeometric differential equation in terms of the Liouville fD in the first step, and then expressed the obtained fD in terms of the hypergeometric function in the second step. His calculation in the second step is unacceptable. In [4] , he gave a derivation of Kummer’s 24 solutions of the hypergeometric differential equation ( [5] , Formula 15.5.4) ( [6] , Section 2.2) by his method. In the present paper, we show that the desired solutions are obtained by using the Riemann-Liouville fD in place of the Liouville fD.

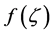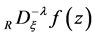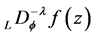In a preceding paper [7] , we discussed the Riemann-Liouville fD and the Liouville fD as analytic continuations of the respective fractional integrals (fIs), on the basis of the papers by Lavoie et al [1] [8] , and those by Nishimoto [3] and Campos [9] , respectively. In Section 2, we define these fIs of a function, and, of order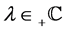, by (1) and (2), respectively, and give their properties which we use later. The notation 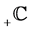is defined at the end of this section.

In Section 3, following [1] [3] [7] -[9] , the Riemann-Liouville fD, 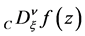and, and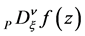 the Liouville f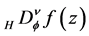D, and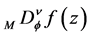, of order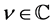, are defined in the form of a contour integral, for a function 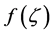which is analytic on a neighborhood of the path of integration. They are defined such that they are analytic continuations of the corresponding fI as a function of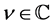. 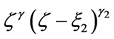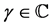In the present paper, the fI and fD are operated to a function of the form for and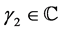. The analytic continuations of and are then shown to be analytic as a function of as well as of and. In the present paper, we use this fact in the calculation. In the following, we use fD to represent fI and fD as a whole.

In [1] , the expression of the hypergeometric function: in terms of the Riemann-Liouville fD is given. In Sections 4 and 4.1, its derivation is presented with the aid of the method using the Riemann-Liouville fD. In Sections 4.2-4.4 and 5, Kummer’s 24 solutions of the hypergeometric differential equation are derived in two ways in the present method.

In a separate paper [10] , a method of obtaining the asymptotic expansion of the Riemann-Liouville fD is presented by using a relation of its expression via a path integral or a contour integral with the corresponding Liouville fD. It is then applied to obtain the asymptotic expansion of the confluent hypergeometric function which is a solution of Kummer’s differential equation. In that paper, Kummer’s 8 solutions of Kummer’s differential equation are obtained by using the method which is adopted in the present paper to obtain the solutions of the hypergeometric differential equation.

We use notations, and, which represent the sets of all complex numbers, of all real numbers and of all integers, respectively. We use also the notations given by, , , for and, and.

2. Riemann-Liouville fD and Liouville fD

Following preceding papers [7] [10] , we adopt the following definitions of the Riemann-Liouville fI, f-dept Liouville fI and the corresponding fDs.

2.1. Riemann-Liouville fI on the Complex Plane

Let and. We denote the path of integration from ξ to z by, and use to denote that the function is integrable on.

Definition 1. Let, , and be continuous on a neighborhood of. Then the Riemann-Liouville fI of order is defined by

(1)

where is the gamma function.

2.2. Definition of f-Dept Liouville fI

Let and. We denote the half line, by, or by. When is locally integrable as a function of t in the interval, we denote this by.

Definition 2. Let, , , and. Let be such that the integral

converges for and diverges for. We then call the abscissa of conver-

gence, and denote it by or.

We then have or.

Lemma 1. Let for and. Then.

Definition 3. Let and. Let and be continuous on a neighborhood of. Let, and. Then we define by

(2)

We call the f-dept Liouville fI of.

Definition 4. When the conditions in Definition 3 are satisfied, we define for by (1).

The following lemma was mentioned in [11] .

Lemma 2. Let. Then

Proof. This is confirmed by comparing the second members of (1) and of (2). ,

2.3. Definitions of Riemann-Liouville fD and Liouville fD

Definition 5. The Riemann-Liouville fD: for and the Liouville fD: for, of order satisfying, are defined by

(3)

when the righthand side exists, where, and for.

Here for denotes the greatest integer not exceeding x.

2.4. Index Law and Leibniz’s Rule of Riemann-Liouville fI and Liouville fI

We use the following index law and Leibniz’s rule, in Section 4.2. By Lemma 2, the formulas for are for the Liouville fI.

Lemma 3. Let, satisfy, and exist. Then

(4)

Proof. Proof for and is found in ( [12] , Section 2.2.6), where p and q appear in place of and, respectively. The proofs there apply for and if we replace p and q in the inequalities there by and, respectively. ,

Lemma 4. Let, and satisfy, and (i) and, or (ii) and. Then (4) holds valid for.

Proof. Proof of (4) for the case (i) is found in ( [7] , Appendix A). In the case (ii), with the aid of this knowledge and formula (3), we prove the first equation in (4) in the following way:

(5)

where, δ = 0 if, and if. When, (5) shows the second equation in (4). ,

Lemma 5. Let, and exist. Then.

Proof. By using the righthand side of (1), we see that both sides of the equation in this lemma are equal to

. ,

This Leibniz’s rule is given in ( [13] , Section 5.5). The following corollary follows from this lemma.

Corollary 1. Let, and exist. Then

(6)

(7)

3. Analytic Continuations of Riemann-Liouville fD and Liouville fD

3.1. Analytic Continuations of Riemann-Liouville fI

In [1] [7] [8] , analytic continuations of the Riemann-Liouville fI via contour integrals are discussed. In [7] , and for are defined as follows.

Definition 6. Let be analytic on a neighborhood of the path and on the point, and. Then is defined by

(8)

for, where the contour of integration is the Cauchy contour shown in Figure 1(a), which starts from, encircles the point z counterclockwise, and goes back to, without crossing the path

. When, we put.

Definition 7. Let, , , and be analytic on a neighborhood of the path and on the points and z. Then is defined by

(9)

for, where is the Pochhammer contour shown in Figure 1(b). When, we put. When, we put.

3.2. Analytic Continuations of Liouville fI

In [3] [7] [9] , the analytic continuation of Liouville fI: is discussed. It is defined in [7] as follows.

Definition 8. Let be analytic on a neighborhood of the path, and and. Then for is defined by

(10)

where. When, we put.

In [7] , another analytic continuation of Liouville fI: was introduced. Here we define it for a function of the form, where, , , and is an entire function.

Definition 9. Let (i): be a function of the form stated above, where, (ii): be the modified Pochhammer contour shown in Figure 2, where, , , , and satisfy, and (iii):, and satisfy, , , and, Then for is defined by

Figure 1. The contours of integration, (a):, (b):.

Figure 2. The contour of integration, from, to X, to, , , Y, , , and then back to.

(11)

where. When, we put. When, is defined by analyticity.

3.3. Analyticity of Riemann-Liouville fD and Liouville fD

In this section, we consider functions and expressed by

(12)

where, , and.

The following Lemmas 6~10 are obtained by modifying the corresponding arguments given in Section 2 for the Riemann-Liouville fD and in Sections 3.1~3.3 for the Liouville fD in [7] , with the aid of ( [14] , Sections 3.1 and 3.2).

Lemma 6. and are analytic as a function of as well as of, and of in the domains and, respectively.

Lemma 7. and are analytic as a function of as well as of and.

Lemma 8. Let exist. Then exists and.

Lemma 9. Let exist. If, then exists and.

Lemma 10. Lemmas 8 and 9 with, , and, replaced by, , and, respectively, are valid.

Remark 1. The statements related with and in Lemma 10 are proved by modifying the proofs of Theorems 3.1 and 3.3, respectively, in [7] .

In the following sections, we use and for the Riemann-Liouville fD.

4. The Hypergeometric Function in Terms of Riemann-Liouville fD

Let, , and satisfy (i): or (ii): and either or. In the case (i), the hypergeometric series is defined by

(13)

where for and, for. In the case (ii), it is defined by

.

The integral representation of is given by

(14)

when, in ( [5] , Formula 15.5.4) ( [6] , Section 2.5). In fact, we obtain (13) from (14) by expanding the righthand side of the latter in powers of z and then performing the integration term-by-term, when.

This function is a solution of the hypergeometric differential equation:

(15)

which has also another solution given by

(16)

see ( [5] , Section 15.5.1) ( [6] , Section 2.2).

4.1. Solution of the Hypergeometric Differential Equation (15) with the Aid of Riemann-Liouville fD

The function is known to be expressed in the form of (18) for given below, in [1] . We now obtain the solutions of (15) expressed in terms of the Riemann-Liouville fD.

Proofs of the following two lemmas are presented in the following two sections.

Lemma 11. Let and for be as follows:

(17)

(18)

where the values a_l, b_l and c_l are given in Table 1, and are constants. Then, for and, are solutions of (15).

Lemma 12. When, we choose, and then given by (18) are expressed as

(19)

Table 1. Values of, and.

Corollary 2. When we put for, we have

(20)

(21)

Remark 2. The solutions given in Corollary 2 satisfy and; see ( [5] , Formulas 15.5.3~15.5.4) ( [6] , Section 2.2). This is confirmed by noting that the solution of (15) in the form with a fixed and is unique.

4.2. Proof of Lemma 11

Lemma 13 Let, and (i): and, or (ii): and, or (iii):, and. Then a solution of (15) is given by

(22)

Proof. We assume that a solution of (15) is expressed as for satisfying. If (i) or (ii) applies, we substitute this in (15), and use Lemma 3 and Corollary 1. We then obtain

(23)

Putting and hence assuming, and applying to (23), we obtain

(24)

with the aid of Lemma 3. This equation requires that

(25)

and when. Now we obtain if any of the three conditions in Lemma 13 is satisfied. Thus we obtain (22). When (iii) applies, we use Lemma 4 in place of Lemma 3. Then we have to use. ,

Remark 3. The proof of Lemma 13 corresponds to the derivation, given in ( [2] , pp. 43-44), of an integral form of the solution of (15), where the method is called the Euler method.

Lemma 14. If is a solution of (15), then for also are solutions of (15).

Proof. We first consider the case of. We replace by in (15), then we obtain

(26)

When we choose, this equation is reduced to (15) with a, b, c and w replaced by, , and u, respectively. In the case of, we use in place of. By using this lemma for and, we see that and are solutions of (15). This proves the case of. ,

Proof of Lemma 11. The formula (18) for follows from Lemmas 13 and 14 with the aid of Lemmas 7-10. ,

4.3. Expressions of in Terms of the Hypergeometric Functions

We now present the expressions of given in (18) in terms of the hypergeometric functions. We then obtain Kummer’s 24 solutions. In the following section, we give another derivation of them.

Proof of Lemma 12 is given at the first part of the proof of Lemma 15 below.

By using Lemmas 8, 9 and 10 and the middle member of (1), (18) is expressed as

(27)

Lemma 15. We choose, , and.

Then given by (18) is expressed as, where

(28)

(29)

if k, , , , , , , , are those given in a row in Table 2.

Proof. We put and in (27). Then we obtain

(30)

when, and also. The data in the row in Table 2, are so chosen that given by (28) with the data is equal to (30). Lemma 12 follows from (30) with the aid of formula (19).

We put and in (27). We then obtain

(31)

when, and. The data in the row are taken from this equation.

We put and in (27). We then obtain

(32)

when, and. The data in the row are taken from this equation.

We put in (28). Then we obtain

Table 2. Functions of z and values of, , , , , and, for.

(33)

Applying this to the formula (28) for and 3, we obtain the results in Table 2 for and 5, respectively. ,

Remark 4. Let given by (29), for and, be denoted by when. We show that they give Kummer’s 24 solutions of (15), which are for given in Theorem 1 below. They are related by for, and by for, where, , , , , , , , , , and for. Here and appear twice, and and do not appear. We note that when the formers are solutions of (15), the latters which are obtained from the formers by exchanging a and b, are obviously solutions of (15). By adding these in the set of solutions, we have the 24 solutions of (15).

Remark 5. In Lemma 15, we have two expressions of for different k. For instance for and, we have, which is given in ( [5] , Formulas 15.3.3~15.3.5) ( [6] , Section 2.4.1).

Remark 6. When, we have, so that the equation (32) and the data for in Table 2 are obtained by using the Liouville fD, and is given by Nishimoto in [4] . In that case, Nishimoto’s derivation is justified.

4.4. Solutions of (15) as a Function of, , , , and

In the following, there appear, , and for. They are listed in Table 3.

Lemma 16. If is a solution of (15), then for also are solutions of (15).

Proof. When, we replace z and by and, respectively, in (15). We then obtain the same equation with c, z and replaced by, and, respectively. We call the obtained Equation (15-2).

When, we put, and replace z and by and or, respectively, in (15). We then obtain

When we choose, this equation is reduced to (15) with b, c, z and replaced by, , and, respectively. We call the obtained Equation (15-3).

Table 3. Fuctions and of z, and values of and, for.

When, we replace and by and, respectively, in (15-3). We then obtain

the same equation with, , and replaced by, , and, respectively.

When, we replace and by and or, respectively, in (15-2).

We then obtain the same equation with b, , and replaced by, , and, respectively. We call the obtained Equation (15-5).

When, we replace and by and, respectively, in (15-5). We then obtain

the same equation with, , and replaced by, , and,

respectively. ,

By Corollary 2 and Lemma 16, we obtain the following corollary.

Corollary 3. Let for represent the righthand side of the equation for given in (20)~ (21). Then for, and,

(34)

is a solution of (15).

We note here the following remark, which is used in obtaining Table 4 below.

Table 4. Functions of z and values of k, l, , , , and for.

Remark 7, for and 5, and for and 6.

5. Kummer’s 24 Solutions of the Hypergeometric Differential Equation

By Corollary 3 and Lemma 7, we obtain the following theorem by the present method.

Theorem 1 We have 24 solutions of (15), which are expressed as

(35)

where the functions of z and the values of, , , and are listed in Table 4.

The values for in Table 4 are obtained by comparing (35) with (20)~(21) in Corollary 2. By Corollary 3 and Remark 7, the functions and the values for are obtained with the aid of the following lemma.

Lemma 17. Let, , , and for represent, , , and, respectively, as a function of a, b and c. Then the values of, , , and and functions of z for are given by

(36)

(37)

(38)

(39)

where and.

The following lemma is well known, see ( [5] , Formulas 15.5.3~15.5.14) ([6] , Section 2.2).

Theorem 2. The solutions given in Theorem 1 for are related by

(40)

Proof. This is confirmed by using Lemma 16 or Corollary 3 with the aid of Remark 2. ,

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Lavoie, J.L., Tremblay, R. and Osler, T.J. (1975) Fundamental Properties of Fractional Derivatives via Pochhammer Integrals. In: Ross, B., Ed., Fractional Calculus and its Applications, Springer-Verlag, Berlin, 327-356. http://dx.doi.org/10.1007/BFb0067118
[2]	Sneddon, I.N. (1980) Special Functions of Mathematical Physics and Chemistry. Longman Inc., New York.
[3]	Nishimoto, K. (1991) An Essence of Nishimoto’s Fractional Calculus. Descartes Press, Koriyama.
[4]	Nishimoto, K. (1997) Kummer’s Twenty-Four Functions and N-Fractional Calculus. Nonlinear Analysis, Theory, Methods & Applications, 30, 1271-1282.
[5]	Abramowitz, M. and Stegun, I.A. (1972) Handbook of Mathematical Functions with Formulas, Graphs and Mathematical Tables, Chapter 15. Dover Publ., Inc., New York.
[6]	Magnus, W., Oberhettinger, F. and Soni, R.P. (1966) Formulas and Theorems for the Special Fuctions of Mathematical Physics, Chapter II. Springer-Verlag New York Inc., New York. http://dx.doi.org/10.1007/978-3-662-11761-3
[7]	Morita, T. and Sato, K. (2013) Liouville and Riemann-Liouville Fractional Derivatives via Contour Integrals. Fractional Calculus and Applied Analysis, 16, 630-653. http://dx.doi.org/10.2478/s13540-013-0040-9
[8]	Lavoie, J.L., Osler, T.J. and Tremblay, R. (1976) Fractional Derivatives and Special Functions. SIAM Review, 18, 240-268. http://dx.doi.org/10.1137/1018042
[9]	Campos, L.M.B.C. (1984) On a Concept of Derivative of Complex Order with Applications to Special Functions. IMA Journal of Applied Mathematics, 33, 109-133. http://dx.doi.org/10.1093/imamat/33.2.109
[10]	Morita, T. and Sato, K. (2015) Asymptotic Expansions of Fractional Derivatives and Their Applications. Mathematics 3, 171-189. http://dx.doi.org/10.3390/math3020171
[11]	Samko, S.G., Kilbas, A.A. and Marichev, O.I. (1993) Fractional Integrals and Derivatives, Theory and Applications. Gordon and Breach Sc. Publ., Amsterdam.
[12]	Podlubny, I. (1999) Fractional Differential Equations. Academic Press, San Diego.
[13]	Oldham, K.B. and Spanier, J. (2006) The Fractional Calculus. Dover Publ. Inc., New York.
[14]	Whittaker, E.T. and Watson, G.N. (1935) A Course of Modern Analysis. Cambridge U.P., Cambridge.