Received 11 December 2015; accepted 31 January 2016; published 3 February 2016
1. Introduction
The chain binomial models (Bailey, 1975) [1] have met with reasonable accomplishment, when fitted to data on communicable diseases for households, for example diseases like common cold or influenza. Also, Heasman and Reid (1961) [2] have demonstrated that the Reed-Frost chain binomial model can provide an adequate fit to data on outbreaks of the common cold in households of size five. And, by comparing the observed frequencies with the expected frequencies for the total number of cases, they also demonstrate that the stochastic version of the Kermack-McKendrick epidemic model (Bailey, 1975) [1] may provide an even better fit. In the later stage, a detailed comparison of the fits provided by these two models is attempted by Becker(1980) [3] by formulating an epidemic chain model, that is developed by assuming a beta distribution of first kind, for the probability of being infected by contact with a given infective from the same household. This model includes, as a particular case, the epidemic chain model corresponding to the stochastic version of the Kermack-McKendrick epidemic model (Bailey, 1975) [1] and, as a limiting case, the Reed-Frost chain binomial model. The advantages of the more general model are also illustrated with an application to household data for the common cold. Also the assumptions made were similar in many ways to those used by Ludwig (1975) [4] in his derivations of the final size distributions for epidemics with arbitrary time-dependent infectiousness.
A more detailed comparison of the fits provided by the two models namely, Reed-Frost chain binomial model and the stochastic version of the Kermack-McKendrick epidemic model, is not attempted by Becker for any epidemic chain model developed by assuming any other kind of Beta distribution for the probability of being infected by contacting with a given infective from the same household. In order to make a more exhaustive comparison, we formulate a modified epidemic chain model by assuming a beta distribution of third kind for the probability of being infected by contacting with a given infective from the same household.
2. Objective
An epidemic chain model was developed by Becker in 1980 [3] by assuming a beta distribution of first kind for the probability of being infected by contact with a given infective from the same household. The main objective of this paper is to provide an alternative epidemic chain model proposed by Becker model (1980) [3] under different assumptions i.e., by developing a modified epidemic chain model by assuming a beta distribution of third kind for the probability of being infected by contact with a given infective from the same household with closed population and to develop the probabilities of all possible epidemic chains with one introductory case for three, four and five member household.
3. Probability of Escaping Infection
Consider a disease say, influenza, which is able to spread from person in a household. Let the time at which the disease is introduced to the household as the time origin and suppose that the outbreak within the household is over by time t*. Assume that during the time interval (0, t*) the chance of infection from outside the household is negligible compared with the chance of infection from within the household. Following a latent period of random duration, an infected person becomes infectious and remains so until his removal by isolation, death or recovery, with immunity for the duration of the outbreak. The probability that a given infected person A, say, transmits the disease to any given susceptible during the time increment (t, t + h) is assumed to be
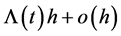
So,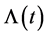 
indicates how infectious A is at time t. By partitioning the interval (0, t*) into n small time increment 
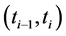of length
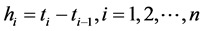, the probability that any given susceptible escapes infection by A during the interval (0, t*) is
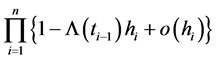
which tends in the limit as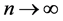 
and the partition becomes finer, to
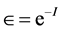, where
.
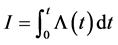In particular case when A assumes the constant value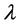 
when A is infectious, but assumes the value zero otherwise , we find that
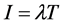, where T is the duration of A’s infectious period and 
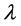is A’s infection rate , so I indicates the potential that A has for transmitting the disease to any given susceptible of the household.
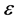, the probability that any given susceptible escapes infection by any given infected person is constant. If both 
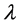and T are constants then 
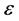is a constant.
4. Chains of Infection
It is not always possible to determine which infective is responsible for a certain infection. It is easier by making use of the gaps between cases, to partition the cases of a household into generations: the susceptible infected by direct contact with the introductory cases are said to make up the first generation of cases; the susceptibles infected by direct contact with first generation cases are said to make up the second generation and so forth. By an epidemic chain we mean the enumeration of the number of cases in each generation.
Thus, we should use 1-2-1-0 to denote the chain consisting of one introductory case, two first generation cases, one second generation case and no cases in later generation.
1-2-1-0
1: Introductory case
2: First Generation case
1: Second generation case
0: Third Generation case
Corresponding to a given infective A, the conditional probability that r out of k susceptibles of the household escape infection by A is
,
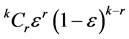given the infection potential I of infective A.
Corresponding to a given infective A, unconditional probability that r out of k susceptibles of the household escape infection A is given by
![]()
(i)
Becker (1980) has considered ![]()
being a beta distribution of first kind given by the density function
![]()
and ![]()
is given by Becker (1980) [3] as
![]()
Now, let us consider ![]()
to be a beta distribution of third kind by Nagar and Ramirez-Venagas (2012) [5] given by the density function
![]()
Then ![]()
is given by![]()
. Since, ![]()
is the probability
of being infected by contact with a given infective from the same household. So the higher herms of ![]()
can be
neglected. ![]()
can further found to be as
![]()
For the practical application the term ![]()
can be considered as
![]()
The above term is resulted after applying the test for convergence of the infinite series
![]()
. In this process Raabe’s test was proved to be stronger than the D’Alembert’s Ratio
test and succeed when the Ratio test fails. For the test of convergence of the infinite beta series, the Raabe’s test is applied when the test fails for the Ratio test.
Further, ![]()
can also be expressed as
![]()
(ii)
where ![]()
Then expression (i) using equation (ii) is given by
![]()
(iii)
To illustrate the computation of the probabilities associated with the different possible epidemic chains we consider the chain 1-1-2-0 in a household of size five including one introductory case. The probability of this chain, conditional on the probabilities ![]()
that a given susceptible escape infection by each of the four infected individuals, respectively found to be
![]()
The unconditional probability is obtained by taking the expectation of this conditional probability and using the fact that ![]()
are independent random variables having the same beta distribution of third kind. Thus the probability of the chain 1-1-2-0 in a household of size five including one introductory case is using the form in equation (ii) we have
![]()
Since, ![]()
, ![]()
and![]()
, so putting the values in the above equation we have
![]()
5. Chain Probabilities
The probabilities of the possible type of chains for household of size three with one introductory case for the probability assuming beta distribution of third kind is given in Table 1. Also, the chain probabilities for households of size three, by assuming the probability as beta distribution of first kind which was earlier developed by Becker in 1980 [3] was also shown in the table along with the new set of expressions. Similarly the expressions are shown in Table 2 and Table 3 for household of size four and five with one introductory case.
6. Conclusion
The paper aims to develop a probability model of infectious diseases which is an alternative to the epidemic chain binomial model of Becker (1980) [3] . This modified epidemic chain binomial model is a complicated
![]()
Table 1. Chain probabilities for households of size three.
![]()
Table 2. Chain probabilities for households of size four.
![]()
![]()
Table 3. Chain probabilities for households of size five.
model than that of the epidemic chain binomial model of Becker, so the estimation procedure for the proposed model is also complicated as compared to the existing epidemic chain binomial model. However, we are in the process of illustrating the application of this method to the data on common cold for three, four, five member household with closed population in our next communication.
Acknowledgements
This work is financially supported by University Grants Commission, New Delhi, under UGC-BSR one time grant (No. F.19-145/2015(BSR)) and provided to the first author.
Conflict of Interest
None.