An Extended Sliding Mode Observer for Speed, Position and Torque Sensorless Control for PMSM Drive Based Stator Resistance Estimator ()
Received 27 August 2015; accepted 1 January 2016; published 4 January 2016

1. Introduction
Drive applications with PMSM are receiving more and more interest because of their better performance in dynamic and steady state responses, from their greater power density, larger torque/ampere, best efficiency, lower cost and easier maintenance [1] [2] . To achieve high-performance field oriented control, accurate rotor position information, which is usually measured by rotary encoders or resolvers, is indispensable. However, the use of these sensors increases the cost, size, weight, and wiring complexity and reduces the mechanical robustness and the reliability of the overall PMSM drive systems.
The goal of the research for this dissertation was to develop a rotor position/speed/load torque sensorless control system with performance comparable to the sensor-based control systems for PMSMs over their entire operating range.
The naturally structure of non-linear multivariable state of PMSM models induces the use of robust feedback linearization method [3] [4] in order to permit a decoupling and good dynamic stability of the PMSM variables in a field-oriented (d, q) coordinate so that stator currents can be separately and independently controlled.
However, this feedback control technique requires the knowledge of the instantaneous speed which is often difficult to access or not usually measurable in practice. Also parameters variations (more specifically the stator resistance and load torque variation) and noises injected by the inverter in the PMSM can induce a lack of field orientation and a state-space “coupling”, which can involve a performance degradation of the system.
In order to achieve better system dynamic performance, the approach proposed in this paper consists to design extended observers allowing an on-line estimation of speed, position, load torque and stator resistance.
The Extended Kalman Filter (EKF) presented in [5] [6] can be used for the problem of states estimations for PMSM sensorless control. Unfortunately the initialization and the optimal choice of covariance and gain matrix are delicate. These matrixes play a critical role in robustness of the EFK.
Another approach proposed in [7] -[10] to estimate the state variables in a PMSM is the use of Sliding Mode Observer (SMO). This nonlinear estimator, based on the variable structure system theory, has been chosen to be of type “Sliding Mode” for having many advantages like: robustness to disturbances, low sensitivity to the system parameters vibrations, some gains easily adjusted compared with the EKF.
Thus, this paper proposes a sixth-order Discrete-time Extended Sliding Mode Observer (DESMO) to provide not only Speed/rotor position estimation but also the load torque and stator resistance reconstruction for the PMSM
After a brief review of the PMSM model, the simulation results for a 1.6 kW PMSM drive system are presented to validate the high robustness of the proposed DESMO approach against parameter variations, measurement and system noises.
2. Model of PMSM
By assuming that the saturation of the magnetic parts and the hysteresis phenomenon are neglected; by considering the case of a smooth-air-gap PMSM (where the inductances are equal: Ld = Lq) and according to the field oriented principle where the direct axis current (Id) is always forced to be zero which simplifies the dynamics and achieve maximum electromagnetic torque per ampere, the PMSM model in the rotor reference (d, q) frame are as follows [2] [5] :
 (1)
(1)
with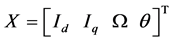 ,
, 
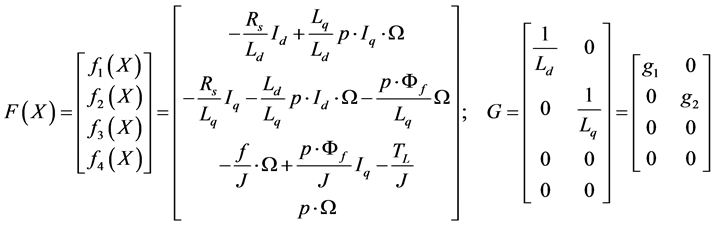
This relation (1) shows that the PMSM dynamic model can be represented as a non-linear function of speed and stator resistance which varies with temperature. A variation of this parameter can induce, for the PMSM, a lack of field orientation, performance and stability. Thus, to preserve the reliability and robustness stability under the stator resistance variation, a robust input-output linearization via feedback control, proposed by [3] [4] , is used to provide a good regulation and convergence of the currents for the PMSM drive. However, the resolution of the feedback control for the PMSM requires an on-line estimation of the speed value that is not measurable.
Thus, in order to take into account the load torque and stator resistance variations, this work uses a full sixth-order Discrete-time ESMO method to provide an on-line estimation of currents, speed, rotor position, load torque and stator resistance in a PMSM.
3. Discrete-Time ESMO Model
Let us consider the dynamic model of the PMSM given by the system (1). Assume that among the state variable, only the currents 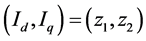 are measurable. Consider that
are measurable. Consider that 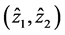 are the estimates of the currents and denote
are the estimates of the currents and denote  the estimates of the speed (Ω) and position (θ). Thus, In order to solve at the same time the problem of the load torque and stator resistance estimations in a PMSM, a six-dimensional extended state vector defined by
the estimates of the speed (Ω) and position (θ). Thus, In order to solve at the same time the problem of the load torque and stator resistance estimations in a PMSM, a six-dimensional extended state vector defined by  has been introduced.
has been introduced.
Thus the proposed ESMO structure is a copy of the model (1), extended to the load torque and stator resistance equation, and by adding corrector gains with switching terms [8] :
 (2)
(2)
with 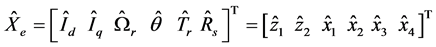
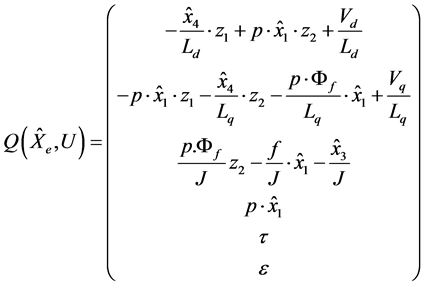
where the parameters (t, e) present the slow variation of (Tr, Rs); K is the observer gain matrices and the switching “Js” that depends on the estimated currents, is given by:
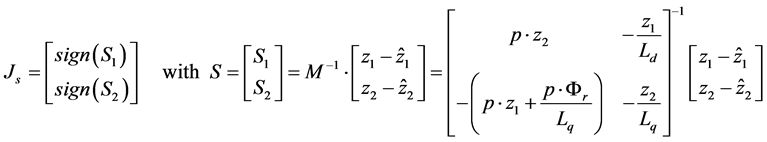 (3)
(3)
Setting

the estimation error dynamics is given by:

The condition for convergence is verified by chosen the following observer gain matrices K1, K2, K3, K4, K5 and K6:
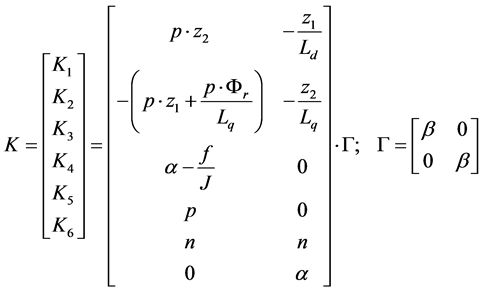 (4)
(4)
From the expression of K, it can be seen that there are three adjusting gains: (a, b and n) > 0, which play a critical role in the potential stability of the scheme with respect to stator resistance, speed and load torque estimation. These three adjusting gains must be chosen so that the estimator satisfies robustness properties, global or local stability, good accuracy and considerable rapidity.
In order to implement the ESMO algorithm in a DSP for real-time applications, the proposed extended sliding mode observer must be discretized using Euler approximation (1st order) proposed in [11] . The Discrete-time Extended Sliding Mode Observer (DESMO) should be written as:
![]() (5)
(5)
with
![]() ,
, ![]()
![]()
![]()
![]()
![]()
where k means the kth sampling time, i.e. t = k∙Te with Te the adequate sampling period chosen without failing the stability and the accuracy of the discrete-time model.
4. Simulation Results and Discussion
Finally, the proposed scheme (Figure 1), a combination nonlinear feedback control and DESMO approach, is carried out for a 1.6 kW PMSM by the simulation on SIMULINK /MATLAB in order to evaluate its robustness and effectiveness in the presence of measurement noise and parameter variations.
The nominal parameters of the PMSM are given in the Table 1. The sampling period is Te = 1 ms.
Two kinds of tests have been performed (with nominal and non-nominal parameters) in order to compare the behaviour of the DESMO algorithm with respect to parameter variation and the presence of about 20% noise on the simulated currents:
![]()
Table 1. Nominal parameters of the PMSM.
・ Figure 2 shows the simulation results with nominal parameters for a load torque (TL = 2 N.m);
・ Figure 3 illustrates the results where the stator resistance varies (Rs = 2.Rsn) with a load torque TL =3 N.m and a step variation in current Id (4 to 3 A).
For each test, the comparative simulation and estimated results are presented. Better estimation performance yielded by the proposed DESMO is obvious from the observation results. Thus it can be seen that the estimation waves are quite similar to the simulation ones. The observed speed, position and load torque indicate the good
![]()
Figure 2. Nominal case (Rs = Rsn): Comparison between estimated and simulated values for TL = 2 N.m in the presence of measurement noise.
![]()
Figure 3. Non Nominal case (Rr = 1.5 × Rrn): Comparison between estimated and simulated values for TL = 3 N.m in the presence of measurement noises.
orientation (the current Iq converges very well to zero) which is due to a favourable stator resistance estimation. Also we can see an absence or a rejection of noises on the speed, position and load torque values in the both figure cases. Furthermore A variation in load torque cannot influence on the speed/position response that remains acceptable.
All those good waveforms show that the agreement between the observation dynamic performance and the simulated ones is demonstrated.
5. Conclusions
In this research, a robust feedback linearization strategy and a DESMO algorithm are used not only to decouple and then control independently the currents of the PMSM in a field-oriented (d, q) coordinate but also to provide the unmeasurable state variable estimation (speed, position, stator resistance and load torque). A series of simulations tests have been achieved on the PMSM. The results obtained have demonstrated a good performance of this robust decoupling controland DESMO algorithm against stator resistance variations, measured noise and load torque.
Thus, in the industrial applications, one will appreciate very well the experimental implement of this robust estimator for the reconstitution of the speed, position and the torque as well as the stator resistance.
Nomenclature
Tem, Tl: Electromagnetic and load torques (N.m).
Id, Iq: (d, q)-axis stator currents (A).
p, J, f: p: pole number; J: inertia (kg∙m2); f: Damping coefficient (Nm.s/rad).
Ld, Lq: (d, q)-axis inductances (H).
Rs, Te: Stator resistance (W) and Sampling period (s).
Vd, Vq: D-axis and q-axis stator voltage (V).
Ff, q: Rotor magnet flux linkage (Wb);q: Rotor position at electrical angle (rpm).
wr, W, wr: Rotor electrical radian speed; W: Mechanical rotor speed (rad/s).
NOTES
![]()
*Corresponding author.