Influence of Magnetic Field, Viscous Dissipation and Thermophoresis on Darcy-Forcheimer Mixed Convection Flow in Fluid Saturated Porous Media ()
1. Introduction
Mixed convective flow and heat transfer in saturated porous media is of practical interest in engineering activities because of its wide applications as seen in porous insulation design, resin transfer modeling, nuclear waste disposal, etc. Over the years, the researchers in the field of fluid mechanics have intensified their research to unravel the importance of particles deposition technology due to its numerous engineering applications. Most of the research efforts as cited in [1] -[4] are concerned about free convection using Darcy’s law, which states that the volume-averaged velocity is proportional to the pressure gradient. The Darcy model has shown to be valid under conditions of low velocities and small porosity. In many practical situations, the porous medium is bounded by an impermeable wall, high flow rates and non uniform porosity distribution in the near-wall region, thereby rendering Darcy’s law inappropriate and inadequate. Hence, to model the real physical situations better, it is therefore necessary to include the non-Darcian effects in the analysis of convective transport in a porous medium.
The problem of Darcy Forchheimer mixed convection heat and mass transfer in fluid-saturated porous media in the presence of thermophoresis was studied by [5] . This phenomenon has been the subject of considerable study in the past. In optical fiber synthesis, thermophoresis has been identified as the principal mechanism of mass transfer as used in the technique of modified chemical vapor deposition (MCVD) [6] . Thermophoresis is a gaseous mixture of active precursors directed over a heated substrate where solid film deposits are located. In particular, the mathematical modeling of the deposition of silicon thin films using MCVD methods has been accelerated by the quality control measures enforced by the micro-electronics industry. Such topics involve a variety of complex fluid dynamical processes including thermophoretic transport of particles deposits, hetero- genous/homogenous chemical reactions, homogenous particulate nucleation and coupled heat and energy transfer.
The migration of small particles in the direction of decreasing thermal gradient is called thermophoresis [7] . That is, a phenomenon which causes small particles to be driven away from a hot surface and towards a cold one. Small particles, such as dust, when suspended in a gas with a temperature gradient, experience a force in the direction of the temperature gradient. The velocity acquired by these particles is called thermophoretic velocity, and the force experienced by the suspended particles due to the temperature gradient is called thermophoretic force. The magnitudes of thermophoretic velocity and thermophoretic force are proportional to the temperature gradient and depend on thermal conductivity of aerosol particles, the carrier gas, the heat capacity of the gas, the thermophoretic coefficient and the Knudsen number. Due to thermophoresis, small micron sized particles are deposited on cold surfaces. In this process, the repulsion of particles from hot objects also takes place, and a particle-free layer is observed around hot bodies [8] .
Thermophoresis is of practical importance in a variety of industrial and engineering applications including aerosol collection, nuclear reactor safety, corrosion of heat exchanger, and micro contamination control. The use of thermophoretic heaters has led to a reduction in chip failures. In the same vein, there is potential application of thermophoresis in removing radioactive aerosols from containment domes in the event of a nuclear reactor accident. [9] was one of the first to study the role of thermophoresis in the laminar flow of a viscous and incom- pressible fluid. He used the classical problem of flow over a flat plate to calculate deposition rates and showed that substantial changes in surface deposition can be obtained by increasing the difference between the surface and free stream temperatures. This was later followed by the effect of thermophoresis on particle deposition from a mixed convection flow onto a vertical plate by [10] and [11] . Also, [12] discussed the effect of surface mass transfer on mixed-convection flow past a heated vertical permeable flat plate with thermophoresis. [13] studied the effect of thermophoretic particle deposition in free convection boundary layer from a vertical flat plate embedded in a porous medium.
Mixed convection flow occurs frequently in nature. The temperature distribution varies from layer to layer and these types of flows have wide applications in industry, agriculture and oceanography. [14] investigated the numerical study on MHD mixed convective flow with dispersion and chemical reaction over a vertical plate in non-darcy porous medium. Transport processes in porous media play a significant roles in various applications such as in geothermal engineering, thermal insulation, energy conservations, chemical catalytic reactors and many others. In many transport processes in nature and in industrial applications, heat and mass transfer with variable viscosity is a consequence of buoyancy effects caused by diffusion of heat and chemical species. [15] investigated the thermophoresis and chemical reaction effects on non-darcy MHD mixed convective heat and mass transfer past a porous wedge in the presence of suction/injection. [16] considered coupled heat and mass transfer in Darcy-Forchheimer mixed convection from a vertical flat plate embedded in a fluid saturated porous medium under the effects of radiation and viscous dissipation. Research on combined heat and mass transfer find application in chemical processing equipment, formation and dispersion of fog, distribution of temperature and moisture over agricultural field as well as grooves of fruit trees, damage of crops due to freezing, food processing, cooling towers, chemically reactive vapor deposition boundary layers in optical materials processing etc. [17] investigated the chemical reaction and radiation effects of surface mass transfer on mixed convection flow past a heated vertical flat permeable plate with thermophoresis. [18] investigates the numerical study of thermophoresis on aerosol particle deposition from hiemenz flow through porous medium onto a stretching sur- face.
The influence of magnetic field on heat and mass transfer by natural convection from vertical surfaces in porous media with Soret and Dufour effects has been carried out by [19] . Analysis of MHD free convection flow along a vertical porous plate embedded in a porous medium with magnetic field and heat generation was in- vestigated by [20] . Viscous dissipation changes the temperature distributions by playing a role like an energy source that leads to affect heat transfer rates. The merits on the effects of viscous dissipation depend on whether the plate is being cooled or heated. The work of [21] deals with the effect of the viscous dissipation term along with temperature dependent heat source or sink on momentum, heat and mass transfer visco-elastic fluid flow over an accelerating surface. [22] investigated the effects of chemical reaction and heat generation on MHD boundary layer flow of moving vertical plate with suction and dissipation. Effects of thermophoresis, practical deposition and chemical reaction on unsteady MHD mixed convective flow over a porous wedge in the presence of temperature dependent viscosity was investigated by [23] . [24] studied the thermophoresis particle deposition and variable viscosity effects on non-darcy free convection in fluid saturated porous media with uniform suc- tion or injection. [25] investigated on the effectiveness of variable heat and mass fluxes on hydromagnetic free convection and mass transfer flow along an inclined permeable stretching surface with thermophoresis. Influence of viscous dissipation on free convection in a non-darcy porous medium saturated with Nano-fluid in the pres- ence of magnetic field was investigated in [26] . [27] investigated the thermophoresis and viscous dissipation ef- fects on Darcy-Forchheimer MHD mixed convection in a fluid saturated porous media.
The effects of magnetic field on a boundary layer control and on the performance of many systems using electrically conducting fluid such as MHD power generators, the cooling of nuclear reactors, plasma studies, purification of molten metals from non-metallic inclusion geothermal energy extraction etc.has been discussed extensively in some literatures. The laminar boundary layer on a moving continous flat surface in the presence of suction and magnetic field was studied by [28] . They observed the effect of magnetic field on boundary layer thickness and skin friction at the surface. Boundary layer flow along a flat plate is considered when a magnetic field acts perpendicular to the plate. Recently, [29] considered the effect of magnetic field on the boundary layer flow, heat and mass transfer of nanofluids over a stretching cylinder. [30] studied the effect of a uniform tran- sverse magnetic field on the stagnation point flow over a stretching and vertical sheet. While, [31] studied the effect of magnetic field on mixed convection boundary layer flow over an exponentially shrinking vertical sheet with suction.
From the literature survey, the influence of magnetic field,viscous dissipation and thermophoresis on Darcy- Forchhemer mixed convection in fluid saturated porous media in the presence of chemical reaction have not been investigated so far. Hence,we result to study the influence of magnetic field and thermophoresis on darcy- forchhemer mixed convection in fluid saturated porous media with viscous dissipation and chemical reaction is investigated using a novel SHAM approach. The transformed governing equations is solved using the spectral homotopy analysis method.
2. Mathematical Formulation
Consider a steady mixed convection boundary layer flow over a vertical flat plate of constant temperature 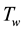 and concentration
and concentration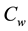 , which is embedded in a fluid-saturated porous medium of ambient temperature
, which is embedded in a fluid-saturated porous medium of ambient temperature 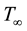 and concentration
and concentration , respectively. The x-coordinate is measured along the plate from its leading edge and the y- coordinate normal to it. Also, it is assumed that there exists a homogeneous first-order chemical reaction with a constant rate
, respectively. The x-coordinate is measured along the plate from its leading edge and the y- coordinate normal to it. Also, it is assumed that there exists a homogeneous first-order chemical reaction with a constant rate 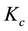 between the diffusing species and the fluid. It is assumed that the porous medium is homo- geneous and present everywhere in local thermodynamic equilibrium. It is to be mentioned that the hole size of the porous plate is assumed to be constant. The fluid state properties and that of porous medium are assumed to be constant. Allowing both Brownian motion of particles and thermophoretic transport, the governing boundary layer equations are
between the diffusing species and the fluid. It is assumed that the porous medium is homo- geneous and present everywhere in local thermodynamic equilibrium. It is to be mentioned that the hole size of the porous plate is assumed to be constant. The fluid state properties and that of porous medium are assumed to be constant. Allowing both Brownian motion of particles and thermophoretic transport, the governing boundary layer equations are
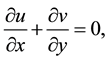 (1)
(1)
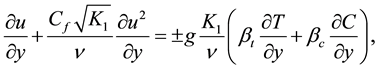 (2)
(2)
 (3)
(3)
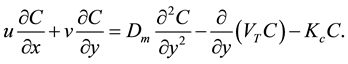 (4)
(4)
The initial conditions at  are given as
are given as
 (5)
(5)
The boundary conditions as  are:
are:
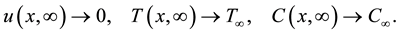 (6)
(6)
In Equation (2), the plus sign corresponds to the case where the buoyancy force has a corresponding “aiding effect” on the flow and the minus sign correspond to “opposing flow” case. The term 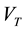 in Equation (4) following [32] can be defined as:
in Equation (4) following [32] can be defined as:
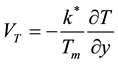 (7)
(7)
setting  and following [33] , the thermophoretic coefficient
and following [33] , the thermophoretic coefficient ![]() is defined as
is defined as
![]() (8)
(8)
The following relations are now introduced for u, v, ![]() and
and ![]() as
as
![]() (9)
(9)
It is well known that boundary layer flows have a predominant flow direction and boundary layer thickness is small compared to a typical length in the main flow direction. Boundary layer thickness usually increases with increasing downstream distance, the basic equations are transformed in order to make the transformed boundary layer thickness a slowly varying function of y, with this objective, the governing partial differential Equations (1)-(4) are transformed by following dimensionless variables for the mixed convection regime:
![]() (10)
(10)
Here, ![]() is the stream function. The first two mathematical relations of (10) satisfy continuity Equa- tion (1). Upon substituting the above transformation (10) into the governing Equations (1)-(4) we obtain the following non-dimensional form
is the stream function. The first two mathematical relations of (10) satisfy continuity Equa- tion (1). Upon substituting the above transformation (10) into the governing Equations (1)-(4) we obtain the following non-dimensional form
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
where the prime denote differentiation with respect to ![]() and the pertinent dimensionless parameters are
and the pertinent dimensionless parameters are
![]()
Also using the above stated similarity transformations, the transformed boundary conditions are:
![]() (14)
(14)
The physical quantities of interest in this problem are Nusselt number and Sherwood number which are de- fined respectively as
Nusselt number:
![]()
Sherwood number:
![]()
3. Approximate Method
In this paper, the numerical version of the homotopy analysis method called SHAM is used to solve a set of or- dinary differential equations (ODEs) that models the problem of darcy-forcheimer mixed convection flow over a vertical plate embedded in a saturated porous medium in the presence of Magnetic field and chemical reaction. SHAM is a numerical version of the homotopy analysis method (HAM) that has been widely applied to solve a wide variety of nonlinear ordinary and partial differential equation with applications in applied mathematics, physics, nonlinear mechanics, finance and engineering. A detailed systematic description of the HAM and its applications can be found in two books (and a huge list of references cited therein) ( [34] [35] ) by S. J. Liao who is credited with developing the method.
In essence, the HAM works by transforming a nonlinear ODE or PDE into an infinite number of linear ODEs which should be solvable analytical. The HAM solutions are required to conform to a predefined rule of solution expression. The SHAM was introduced in ( [36] [37] ) and it uses the principles of the traditional HAM and combines them with the Chebyshev spectral collocation method which is used in the solution of the transformed sequence of ordinary differential equations. One of the main features of the SHAM is the removal of the requirement to conform to a particular rule of solution expression. The SHAM also requires that the linear operator to be used in the development of the algorithm be selected as the entire linear part of the governing differential equation. This often leads to complicated sequence of linear ordinary differential equations which can only be solved numerically. Hence, the use of the Chebyshev spectral collocation method. Spectral methods are now becoming the preferred tools for solving ordinary and partial differential equations because of their elegance and high accuracy in resolving problems with smooth functions ( [38] [39] ).
In applying the spectral-homotopy analysis method, it is convenient to first transform the domain of the
problem from ![]() to
to ![]() and make the governing boundary conditions homogeneous by using the trans- formations
and make the governing boundary conditions homogeneous by using the trans- formations
![]() (15)
(15)
![]() (16)
(16)
Substituting (15)-(16) in the governing equation and boundary conditions (11)-(14) gives
![]() (17)
(17)
![]() (18)
(18)
![]() (19)
(19)
Subject to
![]() (20)
(20)
where the primes denote differentiation with respect to ![]() and
and
![]() (21)
(21)
And
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
The initial approximation is taken to be the solution of the nonhomogeneous linear part of the governing Equa- tions (17)-(19) given by
![]() (25)
(25)
![]() (26)
(26)
![]() (27)
(27)
subject to
![]() (28)
(28)
We use the Chebyshev pseudospectral method to solve (25)-(28). The unknown function![]() ,
, ![]() and
and ![]() are approximated as a truncated series of Chebyshev polynomials of the form:
are approximated as a truncated series of Chebyshev polynomials of the form:
![]() (29)
(29)
![]() (30)
(30)
![]() (31)
(31)
where ![]() is the kth Chebyshev polynomial,
is the kth Chebyshev polynomial, ![]() ,
, ![]() and
and ![]() are coefficients and
are coefficients and ![]() are Gauss- Lobatto collocation points (see [28] ) defined by
are Gauss- Lobatto collocation points (see [28] ) defined by
![]()
Derivatives of the functions![]() ,
, ![]() and
and ![]() at the collocation points are represented as
at the collocation points are represented as
![]()
where r is the order of differentiation and ![]() is the Chebyshev spectral differentiation matrix. Substituting the above expressions in (25)-(28) yields
is the Chebyshev spectral differentiation matrix. Substituting the above expressions in (25)-(28) yields
![]() (32)
(32)
Subject to
![]()
![]() (33)
(33)
where
![]()
And
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() In the above definitions, the superscript T denotes transpose, diag is a diagonal matrix and I is an identity matrix of size
In the above definitions, the superscript T denotes transpose, diag is a diagonal matrix and I is an identity matrix of size ![]() To implement the boundary conditions (33), we delete the first and
To implement the boundary conditions (33), we delete the first and
the last rows and columns of A and delete the first and last rows of![]() ,
, ![]() ,
, ![]() and
and![]() . The boun-
. The boun-
dary conditions (33) are imposed on the resulting first and last rows of the modified matrix A and setting the resulting first and last rows of the modified matrix ![]() to be zero. The values of
to be zero. The values of
![]() are then determined from
are then determined from
![]() (34)
(34)
To find the SHAM solutions of (17)-(19), we begin by defining the following linear operator:
![]() (35)
(35)
![]() (36)
(36)
![]() (37)
(37)
![]() is an embedding parameter and
is an embedding parameter and![]() ,
, ![]() and
and ![]() are the unknown functions. The zeroth order deformation is given as
are the unknown functions. The zeroth order deformation is given as
![]() (38)
(38)
![]() (39)
(39)
![]() (40)
(40)
where![]() ,
, ![]() and
and ![]() are the nonzero convergence controlling auxiliary parameters and
are the nonzero convergence controlling auxiliary parameters and![]() ,
, ![]() and
and ![]() are nonlinear operators given by
are nonlinear operators given by
![]() (41)
(41)
![]() (42)
(42)
![]() (43)
(43)
Differentiating (38)-(40) m times with respect to q and then setting ![]() and finally dividing the resulting equations by
and finally dividing the resulting equations by ![]() yields the mth order deformation equations:
yields the mth order deformation equations:
![]() (44)
(44)
![]() (45)
(45)
![]() (46)
(46)
Subject to
![]() (47)
(47)
where
![]() (48)
(48)
![]() (49)
(49)
![]() (50)
(50)
And
![]() (51)
(51)
Applying the Chebyshev pseudospectral transformation on (44)-(46) gives
![]() (52)
(52)
![]() (53)
(53)
![]() (54)
(54)
Subject to
![]()
![]()
where ![]() and
and![]() , are as defined above and
, are as defined above and
![]()
![]() (55)
(55)
![]() (56)
(56)
![]() (57)
(57)
To implement the boundary conditions above we delete the first and last rows of![]() ,
, ![]() ,
, ![]() and
and ![]()
and delete the first and last rows and first and last columns of ![]() in 52, 53 and 54. The boundary conditions (54a) are imposed on the first and last row of the modified
in 52, 53 and 54. The boundary conditions (54a) are imposed on the first and last row of the modified ![]() matrix on the left side of the equal sign in 52, 53 and 54. The first and last rows of the modified
matrix on the left side of the equal sign in 52, 53 and 54. The first and last rows of the modified ![]() matrix on the right of the equal sign in 52, 53 and 54 are the set to be zero. This results in the following recursive formulas
matrix on the right of the equal sign in 52, 53 and 54 are the set to be zero. This results in the following recursive formulas
![]() (58)
(58)
![]() (59)
(59)
![]() (60)
(60)
Thus, starting from the initial approximation,obtain from (34), higher-order approximations![]() ,
, ![]() ,
, ![]() for
for ![]() can be obtained through the recursive formula (58)-(60).
can be obtained through the recursive formula (58)-(60).
4. Results and Discussion
For the problem under investigation, numerical computations are carried out for different flow parameters such as inertia parameter![]() , thermal rayleigh number
, thermal rayleigh number![]() , buoyancy ratio N, Schmidt number Sc, thermophoretic parameter
, buoyancy ratio N, Schmidt number Sc, thermophoretic parameter![]() , Eckert number Ec, Chemical reaction parameter
, Eckert number Ec, Chemical reaction parameter![]() , Magnetic parameter M and the results are reported in graphs and tables. This is done to illustrate special features of the numerical solutions. In this com-
, Magnetic parameter M and the results are reported in graphs and tables. This is done to illustrate special features of the numerical solutions. In this com-
putation except otherwise stated, we used prandtl number Pr = 0.73, Schmidt number![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() . In addition the boundary condition
. In addition the boundary condition ![]() is approximated by
is approximated by![]() ; which is sufficiently large for the velocity to approach the relevant stream velocity.
; which is sufficiently large for the velocity to approach the relevant stream velocity.
Figures 1-8 illustrate the effects of the various pertinent parameters on the dimensionless velocity![]() , temperature
, temperature ![]() and concentration
and concentration![]() . Figures 1(a)-(c) show the effect of the mixed convection
. Figures 1(a)-(c) show the effect of the mixed convection
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)
Figure 4. Effect of bouyancy ratio parameter N on velocity, temperature and concentration profiles. (a) Velocity profile; (b) Temperature profile; (c) Con- centration profile.
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)
Figure 5. Effect of magnetic parameter M on velocity, temperature and con- centration profiles. (a) Velocity profile; (b) Temperature profile; (c) Concen- tration profile.
![]()
Figure 8. Comparison of velocity profiles of the fluid with the model solved by Kishan [37] . Velocity profile.
parameter ![]() on the dimensionless velocity,temperature and concentration profiles of the flow.We note that when
on the dimensionless velocity,temperature and concentration profiles of the flow.We note that when![]() , the flow is dominated by natural convection, while when
, the flow is dominated by natural convection, while when![]() , forced convection dominates the flow regime. Hence, when
, forced convection dominates the flow regime. Hence, when![]() , the effects of natural convection and forced convection achieve equal importance and flow is dominated by mixed convection conditions. Figure 1(a) shows that velocity of the flow within the boundary layer increases as thermal rayleigh number
, the effects of natural convection and forced convection achieve equal importance and flow is dominated by mixed convection conditions. Figure 1(a) shows that velocity of the flow within the boundary layer increases as thermal rayleigh number ![]() increase due to the effect of buoyancy force. When the free stream and the boundary force are in opposite direction, the bouyancy force retard the fluid on the boundary layer acting somewhat like an adverse pressure gradient. From Figure 1(b) and Figure 1(c), we observed that the temperature and concentration profile of the flow decrease with increasing value of
increase due to the effect of buoyancy force. When the free stream and the boundary force are in opposite direction, the bouyancy force retard the fluid on the boundary layer acting somewhat like an adverse pressure gradient. From Figure 1(b) and Figure 1(c), we observed that the temperature and concentration profile of the flow decrease with increasing value of![]() .
.
Figures 2(a)-(c) illustrate the influence of Eckert number Ec, a viscous dissipation term on the velocity, temperature and concentration distribution. It is observed from these figures that Ec have quite opposite effects on the velocity and the associated thermal boundary layer thickness. That is, velocity and temperature profile of the flow increase with increase in the the viscous dissipation term. This further establishes the fact that Eckert number Ec enhances temperature distribution in a mixed convective flow. Whereas, concentration profile de- creases more quickly for an increasing value of Ec. Figures 3(a)-(c) show the influence of thermophoresis parameter ![]() on the dimensionless velocity, dimensionless temperature and concentration in the presence of viscous dissipation. In Figure 3(a), as a result of viscous dissipation effect which acts as source of internal heat to the flow,the velocity profile increase as a result of increase in thermophoresis parameter. This is accompanied by a slight increase in fluid temperature and concentration as seen in Figure 3(b) and Figure 3(c) respectively. Figure 3(c) illustrates the influence of the thermophoretic parameter on the concentration profiles. It is seen that concentration of the fluid increases with an increase of the thermophoretic parameter
on the dimensionless velocity, dimensionless temperature and concentration in the presence of viscous dissipation. In Figure 3(a), as a result of viscous dissipation effect which acts as source of internal heat to the flow,the velocity profile increase as a result of increase in thermophoresis parameter. This is accompanied by a slight increase in fluid temperature and concentration as seen in Figure 3(b) and Figure 3(c) respectively. Figure 3(c) illustrates the influence of the thermophoretic parameter on the concentration profiles. It is seen that concentration of the fluid increases with an increase of the thermophoretic parameter![]() . So, thermophoretic parameter is expected to alter the concentration boundary layer significantly.
. So, thermophoretic parameter is expected to alter the concentration boundary layer significantly.
Figure 4(a) displays the effects of the ratio of buoyancy parameter N on the velocity, temperature and con- centration profile of the fluid. The effects of the ratio of the buoyancy parameter are similar to that of a local buoyancy parameter in a qualitative way. We noticed that the fluid velocity increases more rapidly in the case of increasing buoyancy parameter. It is observed that velocity increases in the presence of aiding flows![]() . This is because the practical effect of buoyancy ratio N is to enhance the rate of surface heat transfer. Increase in the ratio of the buoyancy parameter correspond to a decrease in the temperature and concentration as observed in Figure 4(b) and Figure 4(c) respectively.
. This is because the practical effect of buoyancy ratio N is to enhance the rate of surface heat transfer. Increase in the ratio of the buoyancy parameter correspond to a decrease in the temperature and concentration as observed in Figure 4(b) and Figure 4(c) respectively.
In Figure 5(a), the velocity of the flow increases with increase in magnetic force acting on the the particles of the fluid. This is because the variation of M leads to the variation of Lorentz force due to the magnetic field, and the Lorentz force produces more resistance to the transport phenomena. Therefore, the momentum boundary layer thickness becomes larger, and the separation of the boundary layer occurs earlier. In Figure 5(b), the fluid temperature increases with an increase in the Magnetic strength. That is, for increasing M it means that magnetic field actually influenced flow system by increasing the values of temperature in the flow field and then de- creasing the gradient at the wall and increases thickness of the thermal boundary layer. While in Figure 5(c), the concentration profile of the flow decreases with increase in the Magnetic parameter M.
The influence of inertia parameter ![]() is illustrated on the velocity, temperature and concentration profiles of the flow as shown in Figures 6(a)-(c). It is observed that an increase in the value of inertia parameter
is illustrated on the velocity, temperature and concentration profiles of the flow as shown in Figures 6(a)-(c). It is observed that an increase in the value of inertia parameter ![]() caused a reduction in the maximum velocity attained by the flow. This occurs as a result of increase in the for- mation of drag within the porous medium when the inertia effect is included. While in Figure 6(b) and Figure 6(c), the temperature and concentration profiles in the boundary layer increase as a result of increase in the inertia parameter and consequently, the thermal and momentum boundary layers become thicker. Figure 7(c) shows the variation of the concentration distribution across the boundary layer for various values of the che- mical reaction parameter
caused a reduction in the maximum velocity attained by the flow. This occurs as a result of increase in the for- mation of drag within the porous medium when the inertia effect is included. While in Figure 6(b) and Figure 6(c), the temperature and concentration profiles in the boundary layer increase as a result of increase in the inertia parameter and consequently, the thermal and momentum boundary layers become thicker. Figure 7(c) shows the variation of the concentration distribution across the boundary layer for various values of the che- mical reaction parameter![]() . It is seen that the effect of increasing values of the chemical reaction parameter result to reduction in the velocity, temperature and concentration distribution across the boundary layer. The reason being that chemical reaction increases the rate of interfacial mass transfer. Figure 8 compared the ve- locity profile of the flow analyzed by [27] and the present study in the absence of magnetic field, chemical re- action and magnetic field. It is observed that the solution obtained by SHAM is in good agreement with Quasi- linearization technique used by [27] .
. It is seen that the effect of increasing values of the chemical reaction parameter result to reduction in the velocity, temperature and concentration distribution across the boundary layer. The reason being that chemical reaction increases the rate of interfacial mass transfer. Figure 8 compared the ve- locity profile of the flow analyzed by [27] and the present study in the absence of magnetic field, chemical re- action and magnetic field. It is observed that the solution obtained by SHAM is in good agreement with Quasi- linearization technique used by [27] .
The effects of thermophoresis, chemical reaction, Hartmann number, on heat flux and mass flux are presented in Tables 1-3 respectively.
As defined previously in the initial/boundary conditions (14), the velocity, temperature and concentration distributions decay as ![]() tends to infinity. The numerical results in Table 1 compared solutions obtained from present model with the one analyzed by [27] on the local heat transfer rate and sherwood number. It is observed that both local heat transfer rate and sherwood number increase as the thermophoresis paramter increases in the flow domain. This further established the accuracy of our results when compared with the earlier work of [27] .
tends to infinity. The numerical results in Table 1 compared solutions obtained from present model with the one analyzed by [27] on the local heat transfer rate and sherwood number. It is observed that both local heat transfer rate and sherwood number increase as the thermophoresis paramter increases in the flow domain. This further established the accuracy of our results when compared with the earlier work of [27] .
![]()
Table 2. SHAM solution for different values of chemical reaction parameter ![]() when
when ![]() .
.
![]()
Table 3. SHAM solution for different values of magnetic parameter M when ![]() .
.
Table 2 illustrates the influence of chemical reaction parameter ![]() on the flow field. It can be seen clearly that local heat transfer rate reduces for every increment in the chemical reaction parameter whereas sherwood number increases with increase in the chemical reaction parametr. Obviously, thermophoresis has direct impact on the concentration profile rather than on the flow velocity and temperature distributions as shown in Table 2. As the chemical reaction species in the flow are multiplied, higher fluid composition can be flushed away from the surface as given in Table 2. Based on Table 3, it can be concluded that as the Hartmann number increases, the Lorentz force due to electromagnetism increases ,leading to increment in internal heat transfer rate.
on the flow field. It can be seen clearly that local heat transfer rate reduces for every increment in the chemical reaction parameter whereas sherwood number increases with increase in the chemical reaction parametr. Obviously, thermophoresis has direct impact on the concentration profile rather than on the flow velocity and temperature distributions as shown in Table 2. As the chemical reaction species in the flow are multiplied, higher fluid composition can be flushed away from the surface as given in Table 2. Based on Table 3, it can be concluded that as the Hartmann number increases, the Lorentz force due to electromagnetism increases ,leading to increment in internal heat transfer rate.
5. Conclusions
In this paper, we have used the spectral homotopy analysis method (SHAM) to solve a second-order nonlinear boundary value problem that governs the two-dimensional steady darcy-forcheimer mixed convection flow in fluid saturated porous media in the presence of chemical reaction and viscous dissipation. The non-linear mo- mentum, energy and species boundary layer equations are transformed into ordinary differential equations using suitable similarity variables.The transformed boundary layer equations are solved using SHAM. We have dis- cussed the effects of magnetic field,chemical reaction,viscous dissipation and thermophoresis on the flow pro- files. The main observations are as follows:
Due to stronger magnetic field the dimensioless velocity decreases whereas, temperature and concentration distributions increase.
An increase in the ratio of the buoyancy parameter N corresponds to an increase in velocity profile ![]() but lead to decrease in the temperature
but lead to decrease in the temperature ![]() and concentration
and concentration ![]() distributions.
distributions.
The fluid velocity and temperature rise with an increase in Eckert number Ec, a viscous dissipation term but caused a reduction the concentration profile.
The influence of thermophoresis parameter on the local heat transfer rate is very significant when compared with the sherwood number.
Using magnetic field we can control the heat and mass transfer flow characteristics.
The species concentration profiles increases significantly for the increasing chemical reaction parameter ![]() and but opposite trend is observed by the influence of thermophoretic parameter
and but opposite trend is observed by the influence of thermophoretic parameter ![]() on the local heat transfer.
on the local heat transfer.
Acknowledgements
We thank the editor and the referee for their useful comments.
Nomenclature
English Symbols
Greek Symbols