A Short Note on Self-Similar Solution to Unconfined Flow in an Aquifer with Accretion

Arieh Pistiner

Unit for Hydrocarbon Pollution Prevention, Ministry of the Environmental Protection, Haifa, Israel.

DOI: 10.4236/ojfd.2015.51007                

Abstract

In this study we refer to a non-steady state, one-dimensional (on the x-axis), unconfined and saturated flow in an aquifer, described by the Boussinesq equation, combined with accretion. In accordance with the above, the moving boundary of the saturated area (toward x → +∝) serves as a horizontal water flux source to the unsaturated area. As time advances, the horizontally saturated zone, lying on the x-axis, becomes wider. A self-similar solution is derived that, after some mathematical manipulation, it is described in terms of Hypergeometric functions. The long-time behaviors of the solution describe the situation at which the water flux, that penetrates horizontally to the non-saturated zone, is equal to the water flux entering into the saturated zone.

Keywords

Boussinesq Equation, Self-Similar Solution, Hypergeometric Function

1. Introduction

In this study, the equation describing unsteady flow in a semi-infinite phreatic aquifer with accretion [1] - [3]

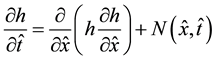, (1)

is analyzed. In the above equation, 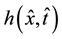is the hydraulic head in the aquifer; 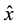and 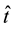are the normalized position and time coordinates, respectively (i.e.,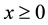), and 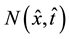is a time and position dependent function, representing the rain intensity distribution imposed on the aquifer that is given by

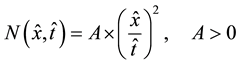(2)

where 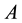is the rain intensity.

We consider a situation in which the water head distribution in a body of water, lying in the porous medium, at time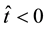, is unknown. Initially, at time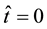, the water level on the inlet face of the aquifer suddenly drops, according to the following power law

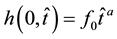, (3a)

where 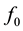is a scaling parameter of the porous medium, and 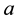is a negative constant to be determined hereafter. This boundary condition would correspond to an influent stream that supplies water to the aquifer. In addition to this, rainwater begins to penetrate into the aquifer according to (2) and adds rainwater to the saturated water body. As a response to that, water flux at the inlet face is created and possesses the following form

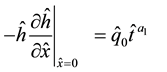, (3b)

where 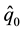is a dimensionless inlet flux parameter and 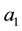is a negative constant to be determined hereafter.

The downstream boundary conditions for the saturated water body on the moving boundary is given by

(3c)

and the downstream water flux on the moving boundary is given by

, (3d)

where is the dimensionless flux parameter of the moving boundary, where the area in the domain, is supposed to be a non-saturated zone.

In general, the problem must be solved for specified initial conditions imposed upon. However, as will be shown below, the long-time profile of is independent of the precise form of the initial condition, which governs the hydraulic head at early stages only. However, the long-time profile will be investigated in the next section by the similarity method.

2. Self-Similar Model

We will now refer to the circumstances in which the hydraulic head in the aquifer achieves a certain asymptotic, and is described by a single independent self-similar variable [4] :

, (4a)

, (4b)

where is a similarity positive function, and are parameters to be determined later. Substituting (2), (4a), (4b) in (1) and after certain mathematical manipulation we obtain

, (5)

where

. (5a)

In this study we refer to the particular case

. (5b)

Introducing (5a) into (5b), we obtain

(6a) (6b) (6c)

Substituting (6b) in (5) and integration we obtain

, (7)

where is an integration constant.

3. Method of Solution

The similarity function may be defined via a new independent function as follows

. (8)

Introducing (8) into (7) combined to yield

. (9)

Define a new dependent variable

. (10)

Introducing (10) into (9) we obtain

, (11)

where

(11a)

We now define two new functions, and respectively

, (12)

and

. (13)

Differentiating with respect to, using (11) and (12) and selecting a value for the rain intensity, i.e., , we obtain an Abel-type equation of the second kind [5]

. (14)

We now define a new function as follows [5]

. (15)

The substitution of (15) in (14) leads to a Riccati equation with respect to

. (16)

We now define the function and apply the Riccati transformation [5] , as follows

. (17)

Substituting (17) in (16), we obtain the following linear ODE

, (18)

where

. (18a)

We now define as follows

, (19)

which is valid in the domain

. (19a)

The substitution of (19) in (18) then yields the hypergeometric equation

, (20)

which possesses the general solution

. (21)

In the above

, (21a)

, (21b)

are expressed via hypergeometric functions [6] , and and are constants to be determined below. Using the properties of the hypergeometric series, we obtain from (21) and (21a), (21b) the expression for

, (22)

where the hypergeometric functions and are given by

, (22a)

. (22b)

Substituting (19) into (17) using (18a) we obtain

. (23)

The introduction of (21) and (22) into (23) we obtain the final solution for

. (24)

Substituting (10) in (13) we obtain

. (25)

The introduction of (8) and (10) into (12) gives the following expression for

. (26)

Using the expression for in Equations (15) and (25) and combined with (26), the functions and are given by

, (27a)

and

, (27b)

where can be easily obtained from (19)

. (28)

The inlet face position, i.e., is obtained from (27a) as follows

. (29)

It can be observed from (23) that the requirement appearing in (29) can be achieved only if. In accordance with the above, we obtained the value for by equating (21) to zero at, i.e.

, (30)

and in accordance with (19a), the constant exists in the following range

. (31)

Substituting (29) in (27b) yields the boundary condition parameter defined in (3a)

. (32)

From the above, it can be observed that must be negative

. (33)

The boundary condition (3c), imposed on the moving front, is determined by equating (27b) to zero by introducing (see (23)). Hence, the downstream parameter (i.e.) is obtained after introducing into (27a). Using the property of the hypergeometric functions (i.e.,) we obtain the downstream parameter

, (34)

where

. (35)

In accordance with the above (i.e.,), the denominator of Equation (34) must obey the following inequality

, (36)

which automatically shows that

, (36a)

and it is in accordance with the range for the parameter in (31).

The behavior of as approaches zero can be obtained from (27b) and is given by

, (37)

where is a positive constant which is equal to.

The flux parameter for the saturated zone, which appear in (3b), can be obtained by using (8)-(13) as follow

. (38)

The water flux parameter on the moving boundary, that serve as water source for the unsaturated zone where (i.e., see (37)), can be obtained from (7)

. (39)

We will now assume that at the long-time limit, the water flux exchange between the inlet face and the moving boundary (i.e., the water flux to the saturated zone and the water flux to the unsaturated zone) reach some equilibrium. As a result, an additional condition can be formulate as follow

. (40)

The introduction of (35) into (39), using (38) and (40) we obtain the following equilibrium equation

, (41)

which is independent on the value of. Solving (41) implicitly and using (30) and (34), we obtain the value for

. (42)

4. Short Discussion

Figure 1 illustrates the evolution of the water head in the aquifer for three time intervals.

Figure 1. Hydraulic head profiles for 3 time intervals (, , , ,).

It can be observed that the downstream branch of the water head profiles is characterized by a steep transition to zero (almost infinite gradient) as can be expected from (38) and (39) (i.e., the water flux on the boundary between the saturated zone and the non-saturated zone possess finite value, as can be observed from (3b) and (3d)).

In general, the solution here developed describes the evolution of the saturated zone, stem from penetration of rainwater and an influent stream from the inlet face. The developed analytical solution can be most useful for verifying numerical solutions involving groundwater transport in an unconfined aquifer.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Bear, J. (1988) Dynamics of Fluids in Porous Media. Dover, New York.
[2]	Knowles, I. and Yan, A. (2007) The Reconstruction of Groundwater Parameters from Head Data in an Unconfined Aquifer. Journal of Computational and Applied Mathematics, 208, 72-81.
[3]	Rai, S.N. and Manglik A. (2012) An Analytical Solution of Boussinesq Equation to Predict Water Table Fluctuations Due to Time Varying Recharge and Withdrawal from Multiple Basins, Wells and Leakage Sites Water Resources Management, 26, 243-252. http://dx.doi.org/10.1007/s11269-011-9915-x
[4]	Barenblatt, G.I. (1979) Similarity, Self-Similarity and Intermediate Asymptotics. Consultants Bureau, New York.
[5]	Polyanin, A.D. and Zaitsev, V.F. (2003). Handbook of Exact Solutions for Ordinary Differential Equations. 2nd Edition, Chapman & Hall/CRC Press, Boca Raton.
[6]	Abramowitz, M. and Stegun, I. (1970) Handbook of Mathematical Functions. Dover, New York.