General Integral Control Design via Singular Perturbation Technique ()
1. Introduction
Integral control [1] plays an important role in practice because it ensures asymptotic tracking and disturbance rejection when exogenous signals are constants or planting parametric uncertainties appear. However, integral control design is not trivial matter because it depends on uncertain parameters and disturbances. Therefore, it is of important significance to develop the design method on the integral control.
In 2009, for overcoming the restriction of traditional integral control, the idea of general integral control firstly was proposed by [1] , which presented some general integrators and controllers. However, their justification was not verified by mathematical analysis. General integral control designs based on linear system theory, sliding mode technique and feedback linearization technique were presented by [2] -[4] , respectively. The main shortage of these design methods proposed by literature [2] -[4] is that they were all achieved by using a kind of particular integrator and linear integral action, which are a serious obstruction to design a high performance integral controller. In addition, general concave integral control [5] , general convex integral control [6] , constructive general bounded integral control [7] and the generalization of the integrator and integral control action [8] were all developed by resorting to an ordinary control along with a known Lyapunov function. This results in that design methods presented by [5] -[8] are all suspended in midair. Thus, it is a very valuable and challenging problem to establish a solid foundation for designing general integral control with the generic integrator and integral control action.
Motivated by the cognition above, this paper proposes a systematic method to design general integral control with the generic integrator and integral control action. The main contributions are that: 1) By mean value theorem, the nonlinear actions in the subsystem and integral dynamics are all reformulated as the linear forms on the interval matrix such that stability theorem of interval matrix can be used to deal with them; 2) The error of integrator output can be used to stabilize the system, just like the system state, such that it does not need to take an extra and special effort to deal with the integral dynamic; 3) No longer resorting to an ordinary control along with a known Lyapunov function, but synthesizing singular perturbation technique, mean value theorem, stability theorem of interval matrix and Lyapunov method, a universal theorem to ensure regionally as well as semi- globally asymptotic stability is established in terms of some bounded information. Consequently, this universal theorem is not suspended in midair but is developed with a solid foundation. Moreover, simulation results showed that general integral controller, which is tuned by this design method, has superstrong robustness and can deal with nonlinearity and uncertainties of dynamics more forcefully.
Throughout this paper, we use the notation 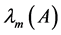 and
and 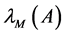 to indicate the smallest and largest eigenvalues, respectively, of a symmetric positive defined bounded matrix
to indicate the smallest and largest eigenvalues, respectively, of a symmetric positive defined bounded matrix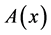 , for any
, for any . The norm of vector x
. The norm of vector x
is defined as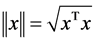 , and that of matrix A is defined as the corresponding induced norm
, and that of matrix A is defined as the corresponding induced norm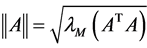 .
.
For two 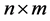 matrices A and B,
matrices A and B, 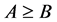 denotes element-by-element inequality. A family of interval matrices is defined as,
denotes element-by-element inequality. A family of interval matrices is defined as,
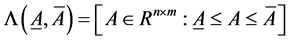
where  and
and 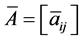 are fixed matrices. The family
are fixed matrices. The family 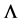 is described geometrically as hyperrectangle in the space
is described geometrically as hyperrectangle in the space 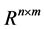 of the coefficients
of the coefficients . We say that a
. We say that a 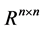 family matrix
family matrix 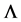 is Hurwitz stable if every
is Hurwitz stable if every ![]() is Hurwitz stable.
is Hurwitz stable.
The remainder of the paper is organized as follows: Section 2 describes the system under consideration, assumption and definition. Section 3 addresses the design method. Example and simulation are provided in Section 4. Conclusions are presented in Section 5.
2. Problem Formulation
Consider the following controllable nonlinear system,
![]() (1)
(1)
where ![]() and
and ![]() are the states;
are the states; ![]() is the control input;
is the control input; ![]() is a vector of unknown constant parameters and disturbances. The partial derivative of function
is a vector of unknown constant parameters and disturbances. The partial derivative of function ![]() on
on ![]() is bounded in the control domain
is bounded in the control domain![]() , and
, and![]() . The functions,
. The functions, ![]() and g are continuous in
and g are continuous in ![]() on the control do- main
on the control do- main![]() . We want to design a control law,
. We want to design a control law, ![]() such that
such that ![]() and
and ![]() as
as![]() .
.
Assumption 1: There is a unique pair ![]() that satisfies the equations,
that satisfies the equations,
![]() (2)
(2)
so that ![]() is the desired equilibrium point and
is the desired equilibrium point and ![]() is the steady-state control that is needed to maintain equilibrium at
is the steady-state control that is needed to maintain equilibrium at![]() .
.
Assumption 2: No loss of generality, suppose that the functions ![]() and
and ![]() satisfies the following inequalities,
satisfies the following inequalities,
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
for all![]() ,
, ![]() and
and![]() . where
. where![]() ,
, ![]() ,
, ![]() and
and ![]() are all positive constants.
are all positive constants.
Definition 1: ![]() with
with![]() ,
, ![]() and
and ![]() denotes the set of all continuously differential increasing functions [8] ,
denotes the set of all continuously differential increasing functions [8] ,
![]()
such that
![]() ,
,
![]()
![]() .
.
where ![]() stands for the absolute value.
stands for the absolute value.
Figure 1 depicts the example curves of one component of the functions belonging to the function set![]() . For instance, for all
. For instance, for all![]() , the functions,
, the functions, ![]()
![]() ,
, ![]() ,
, ![]() and so on, all belong to function set
and so on, all belong to function set![]() .
.
Definition 2: ![]() with
with![]() ,
, ![]() and
and ![]() denotes the set of all integrable func- tions [8] ,
denotes the set of all integrable func- tions [8] ,
![]()
such that
![]() ,
,
![]()
![]()
Figure 1. Example curves of one component of the functions belonging to the function set![]() .
.
hold for all![]() , and
, and ![]() is a point on the line segment connecting
is a point on the line segment connecting ![]() to the origin.
to the origin.
Figure 2 depicts the example curves of one component of the functions belonging to the function set![]() . For instance, for all
. For instance, for all![]() , and
, and![]() , the functions,
, the functions, ![]() ,
, ![]() ,
, ![]() , and so on, all belong to the function set
, and so on, all belong to the function set![]() .
.
3. Control Design
In general, integral controller comprises three components: the stabilizing controller, the integral control action and the integrator, and then the general integral controller can be given as,
![]() (6)
(6)
where![]() ,
, ![]() and
and ![]() are the m × n, m × m and m × m gain matrices, respectively;
are the m × n, m × m and m × m gain matrices, respectively;![]() ;
;![]()
![]() ;
; ![]() is a positive constant; the functions
is a positive constant; the functions ![]() and
and ![]() belong to the function sets
belong to the function sets ![]() and
and![]() , respectively.
, respectively.
Thus, substituting (6) into (1), obtain the augmented system,
![]() (7)
(7)
By Assumption 1 and choosing ![]() to be nonsingular and large enough, and then setting
to be nonsingular and large enough, and then setting ![]() and
and ![]() of the system (7), we obtain,
of the system (7), we obtain,
![]() (8)
(8)
Therefore, we ensure that there is a unique solution![]() , and then
, and then ![]() is a unique equilibrium point of the closed-loop system (7) in the domain of interest. At the equilibrium point,
is a unique equilibrium point of the closed-loop system (7) in the domain of interest. At the equilibrium point, ![]() , irrespective of the value of
, irrespective of the value of![]() .
.
Now, by Mean Value Theorem for each component of the vector function![]() , we have,
, we have,
![]()
where ![]() and
and ![]() is a point on the line segment connecting
is a point on the line segment connecting ![]() to the origin.
to the origin.
For convenience, the function, ![]() can be written as a compact formulation, that is,
can be written as a compact formulation, that is,
![]()
![]()
Figure 2. Example curves of one component of the functions belonging to the function set![]() .
.
where,
![]() .
.
Thus, by the bound of partial derivative of function ![]() on
on![]() , we can ensure that the matrices
, we can ensure that the matrices ![]() and
and ![]() belong to the families of interval matrices, respectively, that is,
belong to the families of interval matrices, respectively, that is,
![]() .
.
In the same way, we obtain,
![]()
Therefore, by![]() , and Definitions 1 and 2, we have,
, and Definitions 1 and 2, we have,
![]() ,
,
and then substituting them and (8) into (7), obtain,
![]() (9)
(9)
where
![]() .
.
Now, defining![]() ,
, ![]() ,
,
![]() ,
,
and then the closed-loop system (9) can be rewritten as,
![]() (10)
(10)
where
![]() ,
,
![]() ,
,
![]() ,
,![]() , and
, and
![]() .
.
In the absence of ![]() and
and![]() , the asymptotic stability of the closed-loop system (10) can be achieved by designing the interval matrices A and
, the asymptotic stability of the closed-loop system (10) can be achieved by designing the interval matrices A and ![]() are all Hurwitz stable [9] . Thus, by linear system theory, two quadratic Lyapunov functions,
are all Hurwitz stable [9] . Thus, by linear system theory, two quadratic Lyapunov functions,
![]() (11)
(11)
![]() (12)
(12)
can be obtained, respectively. Where ![]() and
and ![]() are the solutions of Lyapunov equations
are the solutions of Lyapunov equations ![]() and
and![]() , respectively. It is obvious that
, respectively. It is obvious that ![]() and
and ![]() are all interval matrices, that is,
are all interval matrices, that is,
![]() and
and![]() .
.
Based on the Lyapunov Functions (11) and (12), a composite Lyapunov function candidate [10] for the closed-loop system (10) can be written as,
![]() (13)
(13)
Obviously, Lyapunov function candidate (13) is positive define. Therefore, our task is to show that its time derivative along the trajectories of the closed-loop system (10) is negative define, which is given by,
![]() (14)
(14)
By definitions of ![]() and
and![]() , we have,
, we have,
![]()
![]()
and then substituting![]() ,
, ![]() , and
, and ![]() into
into![]() , and using Assumptions 2, and Definitions 1 and 2, we have,
, and using Assumptions 2, and Definitions 1 and 2, we have,
![]() (15)
(15)
In addition, by![]() ,
, ![]() and definition of
and definition of![]() , obtain,
, obtain,
![]() (16)
(16)
where![]() ,
, ![]() , and
, and ![]() are all positive constants.
are all positive constants.
Substituting (15) and (16) into (14), obtain,
![]() (17)
(17)
where
![]()
The right-hand side of the inequality (17) is a quadratic form, which is negative define when,
![]() (18)
(18)
which is equivalent to,
![]() (19)
(19)
By the dependence of ![]() on
on![]() , it is obvious that the maximum value of
, it is obvious that the maximum value of ![]() occurs at
occurs at ![]() [10] and is given by,
[10] and is given by,
![]() (20)
(20)
It follows that the origin of closed-loop system (10) is asymptotically stable for all![]() . Consequently, by
. Consequently, by ![]() and
and![]() , we have
, we have![]() ,
, ![]() and
and![]() . This means that the closed-loop system (7) is asymptotically stable, too. This established the following Theorem.
. This means that the closed-loop system (7) is asymptotically stable, too. This established the following Theorem.
Theorem 1: Under Assumptions 1 and 2, if there exist gain matrices![]() ,
, ![]() and
and ![]() such that the interval matrices
such that the interval matrices ![]() and
and ![]() are all Hurwitz stable and the following inequality,
are all Hurwitz stable and the following inequality,
![]() (21)
(21)
holds to ensure that there exist positive constants ![]() and
and![]() , and then
, and then ![]() is an exponentially stable equilibrium point of the closed-loop system (7) for all
is an exponentially stable equilibrium point of the closed-loop system (7) for all![]() . Moreover, if all assumptions hold globally, and then it is globally exponentially stable.
. Moreover, if all assumptions hold globally, and then it is globally exponentially stable.
Discussion 1: It is not hard to see that: Just using singular perturbation technique, two key points in stability analysis are solved, that is, one is that it decomposes the whole system into two interconnection subsystems such that it is very easy to obtain two quadratic Lyapunov functions; another is that it derives the condition on the controller gains to ensure the asymptotic stability. Therefore, although mean value theorem, stability theorem of interval matrix, singular perturbation technique and Lyapunov method are all indispensable components, singular perturbation technique plays a decisive role. This is why our design method is called as singular perturbation one.
Discussion 2: By special concerns of the equation ![]() and its matrix
and its matrix![]() , it is not hard to find that the error of integrator output
, it is not hard to find that the error of integrator output ![]() appears in not only the system dynamic
appears in not only the system dynamic ![]() but also the integral dynamic
but also the integral dynamic![]() . This results in that integral dynamic
. This results in that integral dynamic ![]() has the same formulation as the system dynamic
has the same formulation as the system dynamic![]() . Thus, the error of integrator output can be used to stabilize the system, just like the system state
. Thus, the error of integrator output can be used to stabilize the system, just like the system state![]() . This means that in stability analysis, the integral dynamic plays a positive role and it does not need to take an extra and special effort to deal with it. As a result, this is a highlight point of this paper.
. This means that in stability analysis, the integral dynamic plays a positive role and it does not need to take an extra and special effort to deal with it. As a result, this is a highlight point of this paper.
Discussion 3: Compared with general integral control proposed by [2] -[8] , the main differences are that: 1) The integrator and integral action here are all generalized by two function sets, respectively. However, they are all particular in [2] -[4] ; 2) As like reference [7] , the integrator here increases a positive define vector function ![]() on base of the integrator presented by [8] , which can be used as an additional freedom of degree to improve the integrator performance. However, it is not completely freedom and mainly used to construct the bound condition in [7] ; 3) Control design here is achieved by synthesizing singular perturbation technique, mean value theorem, stability theorem of interval matrix and Lyapunov method. However, in reference [2] -[8] , the designs are achieved by linear system theory, sliding mode technique, feedback linearization technique and Lyapunov method, respectively; 4) For the stability analysis, the integral dynamic here not only plays a positive role but also its negative effects can be effectively attenuated by decreasing
on base of the integrator presented by [8] , which can be used as an additional freedom of degree to improve the integrator performance. However, it is not completely freedom and mainly used to construct the bound condition in [7] ; 3) Control design here is achieved by synthesizing singular perturbation technique, mean value theorem, stability theorem of interval matrix and Lyapunov method. However, in reference [2] -[8] , the designs are achieved by linear system theory, sliding mode technique, feedback linearization technique and Lyapunov method, respectively; 4) For the stability analysis, the integral dynamic here not only plays a positive role but also its negative effects can be effectively attenuated by decreasing![]() . However, the integral dynamics not only almost have not positive actions in [5] -[8] but also there no effective method was proposed to deal with its negative effects; 5) Theorem 1 is not suspended in midair but is established on a solid foundation. However, stability theorems [5] -[8] were all developed by resorting to an ordinary control along with a known Lyapunov function.
. However, the integral dynamics not only almost have not positive actions in [5] -[8] but also there no effective method was proposed to deal with its negative effects; 5) Theorem 1 is not suspended in midair but is established on a solid foundation. However, stability theorems [5] -[8] were all developed by resorting to an ordinary control along with a known Lyapunov function.
Discussion 4: From the design procedure above, it is obvious that: First, the equation ![]() in (1) is transformed into the singular perturbation form such that singular perturbation technique can be used to attenuate the nonlinearities and/or uncertainties,
in (1) is transformed into the singular perturbation form such that singular perturbation technique can be used to attenuate the nonlinearities and/or uncertainties,![]() . Second, by mean value theorem, the nonlinear terms,
. Second, by mean value theorem, the nonlinear terms, ![]() ,
, ![]() and
and ![]() are all reformulated as the linear forms on the interval matrix such that stability theorem of interval matrix can be used to deal with them. Finally, by Lyapunov method, a universal theorem to ensure regionally as well as semi-globally asymptotic stability is established in terms of some bounded information. All of them synthesize a systematic method to design general integral control with the generic integrator and integral control action. Specially, the error of integrator output can be used to stabilize the system, just like the system state
are all reformulated as the linear forms on the interval matrix such that stability theorem of interval matrix can be used to deal with them. Finally, by Lyapunov method, a universal theorem to ensure regionally as well as semi-globally asymptotic stability is established in terms of some bounded information. All of them synthesize a systematic method to design general integral control with the generic integrator and integral control action. Specially, the error of integrator output can be used to stabilize the system, just like the system state![]() . All those mean that the design method here can more effectively deal with nonlinearity and uncertainty of dynamics, and then makes the engineers more easily design a stable controller.
. All those mean that the design method here can more effectively deal with nonlinearity and uncertainty of dynamics, and then makes the engineers more easily design a stable controller.
4. Example and Simulation
Consider the pendulum system [10] described by,
![]()
where![]() ,
, ![]() is the angle subtended by the rod and the vertical axis, and
is the angle subtended by the rod and the vertical axis, and ![]() is the torque applied to the pendulum. View
is the torque applied to the pendulum. View ![]() as the control input and suppose we want to regulate
as the control input and suppose we want to regulate ![]() to
to![]() . Now, taking
. Now, taking![]() ,
, ![]() ,
, ![]() and
and![]() , general integral controller can be written as,
, general integral controller can be written as,
![]() ,
,
and then the pendulum system with the normal parameters ![]() and
and ![]() can be written as,
can be written as,
![]() (22)
(22)
where![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
By stability theorem of interval matrix [9] , it is easy to verify that the interval matrix ![]() is Hurwitz stable. Thus, by solving Lyapunov equation
is Hurwitz stable. Thus, by solving Lyapunov equation ![]() and
and![]() , the maximum values of
, the maximum values of ![]() and
and ![]() can be obtained, respectively, that is,
can be obtained, respectively, that is,
![]() and
and![]() .
.
and then using ![]() and
and![]() , we have,
, we have,
![]() ,
,![]() and
and![]() .
.
Therefore, the stability of the closed-loop system (22) can be ensured for all ![]() and
and![]() .
.
For illustrating the performance of controller above, the simulations are achieved under normal and perturbed parameters, respectively. The normal parameters are ![]() and
and![]() . In the perturbed case,
. In the perturbed case, ![]() and
and ![]() are reduced to 0.25 and 2.5, respectively, corresponding to four times the mass.
are reduced to 0.25 and 2.5, respectively, corresponding to four times the mass.
Figure 3 showed the simulation results under normal (solid line) and perturbed (dashed line) cases. The following observations can be made: the optimum response in the whole domain of interest can all be achieved by a set of the same control gains, even under the case that four times payload changes. This demonstrates that although the design method here is too conservative, general integral controller, which is tuned by only the normal parameters, has superstrong robustness, fast convergence, and good flexibility and can deal with nonlinearity and uncertainties of dynamics more forcefully.
5. Conclusions
This paper proposes a systematic method to design general integral control with the generic integrator and integral control action. The main contributions are that: 1) By mean value theorem, the nonlinear actions in the subsystem and integral dynamics are all reformulated as the linear forms on the interval matrix such that stability theorem of interval matrix can be used to deal with them; 2) The error of integrator output can be used to
![]()
Figure 3. System output under normal (solid line) and perturbed case (dashed line).
stabilize the system, just like the system state, such that it does not need to take an extra and special effort to deal with the integral dynamic; 3) No longer resorting to an ordinary control along with a known Lyapunov function, but synthesizing singular perturbation technique, mean value theorem, stability theorem of interval matrix and Lyapunov method, a universal theorem to ensure regionally as well as semi-globally asymptotic stability is established in terms of some bounded information. Consequently, this universal theorem is not suspended in midair but is developed with a solid foundation.
Simulation results showed that general integral controller, which is tuned by this design method, has superstrong robustness and can deal with nonlinearity and uncertainties of dynamics more forcefully.