Inertial and Gravitational Mass Described by Their Electromagnetic Processes ()
1. Introduction
It has been reported that the universe contains a gigantic singularity which generates very low frequency and synchronized TEM (transverse electromagnetic) waves, having extremely high amplitude and energy [1] -[3] . Atoms contain oscillators with different natural frequencies. These oscillators absorb TEM waves at specific frequencies. The absorbed electromagnetic energy accounts for atomic internal and external forces as well as atomic stored energy and emitted energy [1] -[3] . These TEM waves are impossible to measure using state of the art methods. However, a novel method enables exact characterization of TEM waves emitted by the singularity, absorbed by atoms and re-emitted by atoms [1] -[4] .
It has also been reported that atoms absorb these TEM waves in the frequency range 0.005 - 0.03 Hz [1] . The absorbed energy is very large and may account for atomic forces and atomic stored energy.
Furthermore, it has been reported that atoms also absorb TEM waves with frequency 69.9 Hz [2] . These TEM waves are called gravity waves in the present paper. These gravity waves are then re-emitted uniformly into space, whereby some are absorbed by other atoms. This creates a mutual flow of synchronized TEM waves among atoms, resulting in a mutual force of attraction, i.e. gravity.
Gravitational mass is the expression of the mechanism, i.e. intrinsic atomic oscillators, which absorb and re-emit TEM waves resulting in the gravitational force [2] .
It has also been reported that excess energy quanta hv in oscillators, contained in a particle, an electron or an atom, is superpositioned on gravity waves absorbed by the oscillator. The re-emitted TEM wave has the superpositioned energy quanta hv and the frequency 69.9 Hz + v [3] . The superpositioned energy quantum hv is called photon and it explains the photon—wave duality. Empiric results reveal that this process is frequency independent [3] [4] .
Consequently, acceleration or deceleration of a particle, an electron or an atom, results in generated and emitted photons. Acceleration or deceleration of a particle, an electron or an atom demands enforced force and energy. The enforced energy equals the emitted photon energy. Thus inertial mass is the expression of the mechanism, i.e. intrinsic atomic oscillators, which superpose excess energy quanta hv on absorbed and re-emitted TEM waves. Thus, inertial mass is the expression of the mechanism which transforms enforced energy into emitted electromagnetic energy.
Hence, gravitational and inertial mass can be described by the electromagnetic interaction between particles, electrons or atoms and omnipresent electromagnetic energy generated by a singularity.
The objective with the present paper is to build on results already presented in reports [1] -[4] . This information is compiled into a theoretical model in Section 2, which describes the mechanism behind gravitational and inertial mass. The theoretical model is based on state of the art electromagnetic and wave theory [5] -[11] and photon theory [12] -[14] . In Section 3 the theoretical model is compared with state of the art description of inertial mass based on the Higgs field, the Higgs mechanism and the Higgs particle [15] -[21] . Discussion and conclusions are found in Section 4.
The aim of the study is to present a theoretical model of gravitational and inertial mass.
2. Theoretical Model
2.1. Gravity
The theoretical model builds on the observation that atomic oscillators69.9, with natural frequency 69.9 Hz, absorb TEM waves with frequency 69.9 Hz [2] . The TEM waves originate from a singularity in the universe and have been thoroughly described [1] -[3] . The absorbed TEM waves are then re-emitted uniformly into space.
The behavior and characteristics of plane TEM waves is independent of their frequency. The field vectors E and B or H (B = µ0H) are linked and perpendicular. The field vector amplitudes relate as E = cB, where c is the speed of light. The electric and magnetic field vector amplitudes E and B decrease with the distance from the source as 1/r. The Poynting vector S describes the TEM energy flow density [5] [6]
 (1)
(1)
The energy stored in the magnetic field is just equal to that in the magnetic field. The direction of energy flow is reversed for a wave travelling in the opposite direction because the phase of E and H is reversed.
Assume that one source, Source 1, absorbs and re-emits plane TEM1 waves, described by its Poynting vector S1(r) at the distance r from Source 1. Another source, Source 2 is positioned at the distance r. Source 2 absorbs TEM waves and re-emits plane TEM2 waves uniformly into space. In the direction towards Source 1 plane TEM1 and TEM2 waves interact because of the force between their synchronized field vectors. This also implies that there is energy transfer from TEM1 to TEM2 when TEM2 propagates towards Source 1. In equilibrium there is energy transfer in both directions, i.e. from TEM1 to TEM2 vice versa. Note that E and H are always perpendicular and hence S = E × H can be replaced by S = E·H. Equilibrium is defined by the amount of energy that Source 1 is able to deliver at Source 2, e.g. at the distance r, S1(r), and the amount of energy that Source 2 is able to deliver at Source 1, i.e. S2(r). This results in back reaction force F(r), i.e. radiation reaction [5] . This creates mutual force of attraction F(r), and where γ is a constant:
 (2)
(2)
It is now assumed that each source consists of many oscillators69.9 where each atomic oscillator69.9 re-emits TEM waves described by its Poynting vector 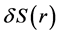 and where r denotes the distance from the source and its oscillator69.9. E and H decrease linearly with the distance r implying that
and where r denotes the distance from the source and its oscillator69.9. E and H decrease linearly with the distance r implying that  decreases with the square of the distance;
decreases with the square of the distance;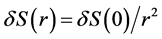 . The mutual force of attraction
. The mutual force of attraction  between two atomic oscillators69.9 and distance r is
between two atomic oscillators69.9 and distance r is
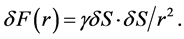 (3)
(3)
It is now assumed that one oscillator69.9 acts on p co-located oscillators69.9, belonging to the set P of all oscillators69.9 at Source 2, and where each force can be described by . These oscillators69.9 are synchronized resulting in the force
. These oscillators69.9 are synchronized resulting in the force
 (4)
(4)
It is now assumed that n co-located oscillators69.9, belonging to the set N of all oscillators69.9 at Source 1, act on p collocated oscillators69.9, belonging to the set P of all oscillators69.9 at Source 2, resulting in the total force F(r)
 (5)
(5)
δS·δS is a constant described by the intrinsic characteristics of the oscillator69.9, and hence Equation (5) is simplified into
 , (6)
, (6)
where ξ is a constant.
In a previous study Equation (6) was called the law of gravity between two clusters, at distance r containing n respectively p oscillators69.9 [2] . Note that the cluster can be few oscillators69.9, an electron, an atom, a mass, a planet or a black hole.
Equation (6) can be illustrated with gravity between the earth and the sun. The earth contains n atomic oscillators69.9 creating a force nδF(r) on every atomic oscillator69.9 in the sun. The sun contains p oscillators69.9, thus the total force of attraction is npδF(r) and that is equal to Equation (6). The earth’s mass m1 is proportional to the number of atomic oscillators69.9 on earth, i.e. m1 ~ n, and the sun’s mass m2 ~ p. Equation (6) is then approximately equal to the Newtonian geometric law of gravity, where FG is the gravitational force:
 (7)
(7)
S1(r) and S2(r) in Equation (6) depend on the distance between the singularity and S1(r) respectively S2(r). Thus ξ in Equation (7) increases at decreasing distance to the singularity.
Gravity is illustrated in Figure 1.
Comment; Gravity encompasses altogether four oscillators at 69.9 Hz, 71.9 Hz. 89.9 Hz and 91.9 Hz. Together they form clusters and the sum of F(r) in Equation (6) of all four forces comprises, according to the superposition principle, a static force. This explains why gravity is a static force. This will be explained in detail in a forthcoming study. In this study only the contribution from 69.9 Hz is described in order to simplify. In the text 69.9 Hz can be substituted with 69.9 Hz, 71.9 Hz. 89.9 Hz and 91.9 Hz in order to gain a correct description.
2.2. Photon
The amplitude of light and radio waves decreases linearly with the distance r from the source (as 1/r). One commonly known phenomenon in physics which decreases linearly with distance is the far field from accelerated charge, i.e. the plane TEM wave according to Maxwell’s equations [5] [6] :
 (8)
(8)
 (9)
(9)
According to state of the art science radio waves are generated by accelerated electrons in the antenna which produces a far field according to Equations (8) and (9). This far field is a plane TEM wave. This TEM wave can be absorbed (e.g. in matter or receiver antenna) whereby its energy is dissipated as e.g. heat or current in the

Figure 1. A singularity 1 generates gravity waves (low frequency plane TEM waves). Oscillators69.9 2 and 3 in atoms create resonance with gravity waves and re-emit them unaltered. This causes flow of gravity waves between atoms and their oscillators69.9 2 and 3. The flow of gravity waves in opposite directions between oscillators69.9 results in mutual force of attraction, i.e. gravity.
antenna and which results in that the TEM wave ceases to exist.
The real process is very different; however, the end result is almost the same. The theory of photon energy transport in space can be illustrated with radio waves. It has been shown [3] that radio waves are the result of the sum of time limited processes, i.e. acceleration or deceleration of oscillators69.9 in an electron or atomic nucleus, see Figure 2. These oscillators69.9 absorb and re-emit gravity waves with frequency 69.9 Hz. Accelerating or decelerating an electron or an atomic nucleus implies that they gain energy, i.e. each of their intrinsic oscillators69.9 increases its energy and this excess energy can be described by one or many energy quanta hv. In this case the oscillator69.9 4 in the electron or atom contains one energy quantum hv at a time, where h is Planck constant or quantum of action. The energy quantum hν is discrete and limited in time. The energy quantum hν is superpositioned on a re-emitted TEM wave. This TEM wave contains the superpositioned energy quantum hv and the frequency 69.9 Hz and instant frequency ν. Hence, the re-emitted wave is a gravity wave with superpositioned electromagnetic energy. The superpositioned electromagnetic energy quantum hv with frequency v is the photon. In a continuous process the sum of many photons and their energy quanta hν, superpositioned on re-emitted gravity waves, result in radio waves. The radio wave’s amplitude is proportional to the number of photons per time unit, which is proportional to the number of involved energy quanta hv, which in its turn is proportional to the number of involved oscillators69.9 and which is proportional to the inertial mass. This radio wave has the frequency 69.9 Hz + v.
The radio wave can be absorbed in matter 5 and where the superpositioned energy quanta hν are absorbed, resulting in that the radio wave is converted back to the original gravity wave with frequency 69.9 Hz.
The energy contained in a TEM wave is proportional to its frequency ν. From this follows that the superpositioned energy and the photon energy δE is:
 (10)
(10)
The TEM wave’s superpositioned energy and momentum are related as δE = pc, where p is the magnitude of the momentum vector p. This derives from the following relativistic relation, with m = 0 [11] :
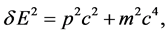 (11)
(11)
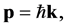 (12)
(12)
where k is the wave vector (where the wave number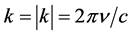 ), and
), and  is the reduced Planck
is the reduced Planck

Figure 2. Electrons can be accelerated or decelerated. The electron contains oscillators69.9. The oscillator69.9 4 in an electron creates resonance with a gravity wave and excess energy hν, caused by electron acceleration deceleration, is superpositioned on the re-emitted wave. The superpositioned energy hv with frequency v represents the photon. This wave with frequency 69.9 Hz and v is re-emitted as a radio wave. The superpositioned energy hν can be absorbed in matter 5, whereby the radio wave is converted into the original gravity wave with frequency 69.9 Hz.
constant. Since p points in the direction of the TEM wave propagation, the magnitude of the momentum is:
 (13)
(13)
Thus, the photon contained in the radio wave is not a particle; however, discrete electromagnetic energy quantum hν, with frequency v, superpositioned on a low frequency TEM wave, i.e. a gravity wave. From this follows that the photon is strictly mass less, has zero charge and propagates with the speed of the low frequency TEM wave, i.e. with the speed of light in free space.
Previous reports have shown that this process is frequency independent. Currents in the magnetosphere generate photons or radio waves with the period 24 hours [4] . It is possible to generate photons or radio waves in the 2 Hz - 2 GHz range using a signal generator or a radio transmitter [3] . Photons in the 400 to 700 nanometer range are produced by a similar process [3] when matter is heated. Hence, the theoretical model is valid from almost infinite period to almost infinite frequency.
2.3. Gravitational Mass
From Equation (5) follows that the gravitational force FG acting on an oscillator69.9 or a cluster of n oscillators69.9 (e.g. oscillators69.9 contained in electron, atom, mass, planet) is the result of TEM waves operating on the oscillator69.9 or the cluster of n oscillators69.9. Hence, the force FG is proportional to the sum of involved oscillators69.9.
 (14)
(14)
This implies that the gravitational mass mG is the expression of the mechanism which results in the gravitational force FG:
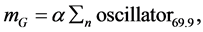 (15)
(15)
where α is a constant.
This also implies that Einstein’s E = mc2 is incorrect. Absorbed TEM waves with frequency 69.9 Hz do not result in nucleus energy. It is proposed that energy E, stored in a body, is the result of TEM waves absorbed by atomic oscillators (with natural frequencies in another frequency range), reported previously [1] . However, the number of these atomic oscillators is proportional to the number of atomic oscillators69.9 with natural frequency 69.9 Hz, and proportional to the mass mG. Hence, E = mc2 is correct in a wide sense.
2.4. Inertial Mass
The implication of Section 2.2 is as follows. Accelerating or decelerating an oscillator69.9 or a cluster of n oscillators69.9 (e.g. particle, electron, nucleus, atom, body, mass, car or planet) results in emitted photons, i.e. emitted electromagnetic energy. Hence, the force FI and the energy EI must be enforced on the oscillator69.9 or n oscillators69.9 in order achieve acceleration or deceleration. The enforced energy EI equals the sum of the energy in emitted photons. Thus, enforced energy is transformed into emitted electromagnetic energy.
The force δFI must be enforced on one oscillator69.9 in order to achieve the acceleration or deceleration β·a, where β is a constant and a is the acceleration. In order to accelerate or decelerate n oscillators69.9 the force FI must be enforced on the oscillators69.9:
 (16)
(16)
In classical mechanics Equation (16) is denoted FI = mIa. Consequently, the inertial mass mI is the expression of the mechanism which transforms enforced energy into emitted electromagnetic energy:
 (17)
(17)
From Equation (15) and Equation (17) follows that the gravitational mass relates to the inertial mass; . This explains the linear relationship between gravitational and inertial mass, as observed in classical mechanics.
. This explains the linear relationship between gravitational and inertial mass, as observed in classical mechanics.
Inertial mass can be illustrated with the following. Enforced force FI and energy EI accelerates the mass mI, resulting in that photons are emitted and where the photon energy equals EI. When FI is removed the mass mI propagates with constant velocity in free space. This implies that the mass does not emit photons, i.e. the transport is loss free. Now the force FI and energy EI is enforced on the mass mI, which results in that the mass is decelerated whereby photons are emitted, and where the photon energy equals EI. In classical mechanics the kinetic energy is . However, this energy is not stored in the mass, i.e. the kinetic energy EK does not exist. EK expresses that a mass mI with velocity v can be decelerated to the velocity v = 0 in a given reference system. This results in that photons are emitted and where the total photon energy is
. However, this energy is not stored in the mass, i.e. the kinetic energy EK does not exist. EK expresses that a mass mI with velocity v can be decelerated to the velocity v = 0 in a given reference system. This results in that photons are emitted and where the total photon energy is
 (18)
(18)
Consequently, accelerating mass results in that enforced energy EI is emitted as photon energy EI, and it is not stored as kinetic energy EK. Mass deceleration results in that that the enforced energy EI is emitted as photon energy EI, and there is no other energy involved, i.e. kinetic energy.
3. Alternative Theory
The Higgs field, the Higgs mechanism and the Higgs particle provide an alternative description of inertial mass. The drawback with that theory is that the Higgs field and the Higgs mechanism are based entirely on the theoretical mathematical description of a scalar field which we do not know if it exists, nor has this field and mechanism been measured and empirically verified. The existence of the Higgs particle has been reported [21] .
The strength of the present theory is that there exists a method to measure relevant parameters [1] -[4] . TEM waves originating from the singularity have been measured to a degree which allows exact description of their characteristics such as direction of origin, amplitude, phase, frequencies and field vector behavior [1] -[3] . Furthermore, TEM waves, absorbed and re-emitted by atoms, have been measured to a degree which reveals the atomic intrinsic mechanism; forced damped oscillators with natural frequencies 0.005 - 0.03 Hz [1] and 69.9 Hz [2] . Moreover, extremely low frequency photons have been produced and measured in laboratory [3] . Hence, crucial parts of the present theory have been measured in laboratory and some parts have been simulated and reproduced in laboratory.
4. Discussion and Conclusion
It is proposed that all energies in the universe originate from a singularity, and are distributed throughout the universe by low frequency TEM waves, having a broad spectrum of frequencies. The atom in itself is fully passive. At this stage the atom’s physical view is of little interest. However, the atom’s functional view is crucial; the atom consists of forced damped oscillators with different natural frequencies. They absorb TEM waves originating from the singularity. The atomic oscillators are assembled in different configurations, where the number of oscillators and their mix of natural frequencies result in different types of electromagnetic energies and forces, according to electromagnetic theory [5] [6] and wave theory [7] -[11] . One configuration results in that the absorbed energy creates internal forces and nuclear binding energy [1] . A second configuration results in that the absorbed energy generates what is perceived as static electric fields, e.g. the Coulomb field [1] . A third configuration results in that absorbed energy is re-emitted creating gravity, photon, gravitational mass and inertial mass [2] [3] . All of these processes are entirely electromagnetic. These processes originate from external electromagnetic energy operating on fully passive atoms and where the atom contains only one type of functionality, and force damped oscillators.
The platform of modern physics is elementary particle physics described in the Standard Model [12] . Atom, photon and graviton are described as particles. The atom is self contained, i.e. atomic forces and energy are the consequence of atomic intrinsic mechanisms. The Higgs field is added in order to account for inertial mass.
Consequently, there is a fundamental difference between the present theoretical model and the Standard Model and they provide fundamentally different solutions to the basic level of physics.
The present paper describes that gravitational mass mG is the expression of the mechanism which results in gravitational force FG. Inertial mass mI is the expression of the mechanism which transforms enforced energy EI into emitted electromagnetic energy EI. In both cases the mechanism consists of external energy operating on atomic oscillators69.9 with natural frequency 69.9 Hz. The present study describes gravity and photon by their electromagnetic processes. The present study also displays that gravitational and inertial mass are caused by electromagnetic processes.