1. Introduction
Other classical nonlinear equation which has been the object of much study is called the white-dwarf equation. This equation has the form:
 (1)
(1)
with  and subject to initial conditions:
and subject to initial conditions:
 (2)
(2)
The Equation (1) is one of Lane-Emden types, where
 . In fact, it reduces to Lane-Emden equation with index
. In fact, it reduces to Lane-Emden equation with index  when
when .
.
Let us consider a spherical cloud of gas (see Figure 1) and denote its hydrostatic pressure at a distance  from the centre by P. Let
from the centre by P. Let 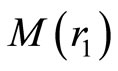 be the mass of the spheres of radius
be the mass of the spheres of radius  the gravitational potential of the gas, and g the acceleration of gravity.
the gravitational potential of the gas, and g the acceleration of gravity.
Then, we have the following equations:
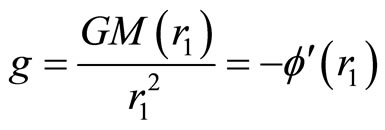 (3)
(3)
where G is the gravitational constant.
Thus, three conditions are assumed for the determination of  and P:
and P:
 (4)
(4)
where ρ is the density of the gas.
 (5)
(5)
and
 (6)
(6)
where γ and K are arbitrary constants.
Solving (4) and (6) with  when
when  we have:
we have:
 (7)
(7)
or
 (8)
(8)
where  and
and . If this value of ρ is replaced into Equation (5), we obtain:
. If this value of ρ is replaced into Equation (5), we obtain:
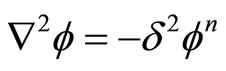 (9)
(9)
where, .
.
This is the Lane-Emden equation. This is a second order ordinary differential equation for the density profile ϕ as a function of the radius . We also have to determine initial conditions at
. We also have to determine initial conditions at . Obviously, at the center the density has to be the central density, and hence
. Obviously, at the center the density has to be the central density, and hence  at
at . Also, the derivative of the density has to vanish at the center, and therefore
. Also, the derivative of the density has to vanish at the center, and therefore  at
at .
.
Our goal is to find a function ϕ that satisfies the Lane-Emden Equation (9). In general, this has to be done numerically using the differential transformation method.
The Zhou’s Method is a semi-numerical-analytic method for solving ordinary and partial differential equations. The concept of the DTM was first introduced by Zhou in 1986 [2]. Its main application therein is to solve both linear and non-linear initial value problems in electric circuit analysis. This technique constructs an analytical solution in the form of a polynomial. The Taylor series method is computationally expensive for large orders. The differential transformation method is an alternative procedure for obtaining analytic Taylor series solution of the differential equations. The series often coincides with the Taylor expansion of the true solution at point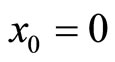 , in the initial value case, although the series can be rapidly converged in a very small region.
, in the initial value case, although the series can be rapidly converged in a very small region.
Many numerical methods were developed for this type of nonlinear ordinary differential equations, specifically on Lane-Emden type equations such as the Adomian Decomposition Method (ADM) [3,4], the Homotopy Perturbation Method (HPM) [5,6], the Homotopy Analysis Method (HAM) [7] and Bernstein Operational Matrix of Integration [8], in [9] Hojjati and Parand propose a class of second derivative multistep methods (SDMM) for solving some well-known classes of Lane-Emden type equations. Finally in [10] Batiha propose the variational iteration method (VIM) for a class of Lane-Emden type equation, powerful method for the solution of linear and nonlinear equations. In this paper, we show superiority of the DTM by applying them on the some type LaneEmden type equations (white-dwarfs).
2. Differential Transformation Method
Differential transformation method of function  is defined as follows:
is defined as follows:
 (10)
(10)
In (10),  is the original function and
is the original function and  is the transformed function and the inverse differential transformation is defined as:
is the transformed function and the inverse differential transformation is defined as:
 (11)
(11)
In real applications, function 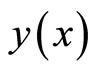 is expressed by a finite series and Equation (11) can be written as:
is expressed by a finite series and Equation (11) can be written as:
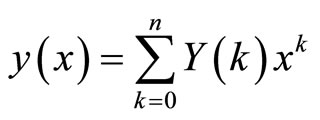 (12)
(12)
Equation (12) implies that
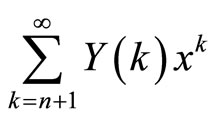
is negligibly small. Here, n is decided by the convergence of natural frequency in this study.
The following theorems that can be deduced from Equations (10) and (11).
Theorem 1.1. If
 then
then 
Theorem 1.2. If
 then
then 
 is a constant.
is a constant.
Theorem 1.3. If
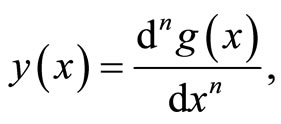 then
then 
Theorem 1.4. If
 , then
, then 
Theorem 1.5. If
 then
then where
where

Theorem 1.6. (Cárdenas A). If  with
with  then:
then:

Proof. We proof this theorem by induction method. We assume that is true for m, then we will prove that is true also for . Using DTM to a product we have:
. Using DTM to a product we have:

then,

where  and
and  Therefore,
Therefore,
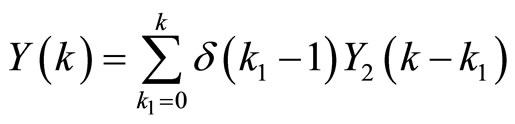
whenever  the expression reduces to:
the expression reduces to:

Now, if  then all terms of the sum are zero except $
then all terms of the sum are zero except $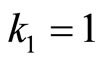 obtaining:
obtaining:

Rearranging the expression we have:


The proofs of Theorems 1-5 are available in [1].
3. Numerical Solution for C = 0.3
To illustrate the ability of the Zhou’s method for the Lane-Emden type equation (white-dwarf), the next problem is provided for . The results reveal that this method is very effective.
. The results reveal that this method is very effective.
Problem. To solve  subject to
subject to  and
and . First, multiplying both sides by x we have:
. First, multiplying both sides by x we have:
 (13)
(13)
Here, is easy to verify that the function

has a series expansion:
 (14)
(14)
where  Therefore, (13) takes the form:
Therefore, (13) takes the form:
 (15)
(15)
Using in (15) the Theorems 3, 4 and 6 we have:
 (16)
(16)
or
 (17)
(17)
where,



and successively. Also,
 (18)
(18)
 (19)
(19)
 (20)
(20)
for all .
.
Now, from the initial conditions  and
and  we have:
we have:
 (21)
(21)
Substituting Equation (21) into Equation (17) and by recursive method, the results are listed as follows:
For  we have:
we have:

For 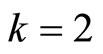 we have:
we have:

and then, .
.
For  we have:
we have:
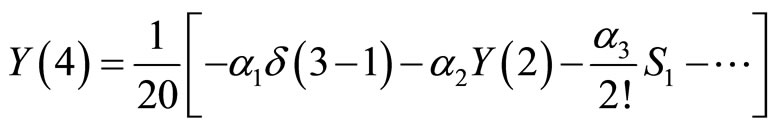
and then,

For  we have:
we have:
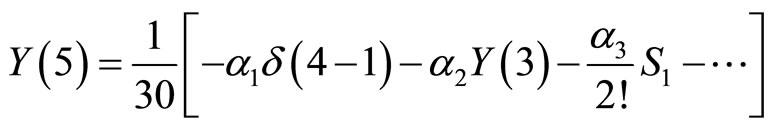
and then, 
For  we have:
we have:
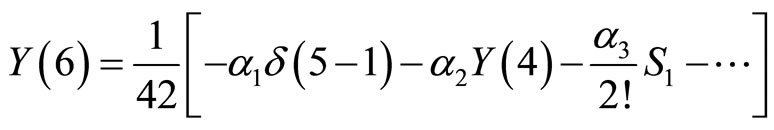
and then,

Therefore using (12), the closed form of the solution can be easily written as:

A series solution obtained by Chandrasekhar [2] using series expansion was:

Table 1 shows the comparison of  obtained by the DTM (method proposed in this work) and those obtained by Hojjati. The resulting graph of the whitedwarfs equation in comparison to the present method and those obtained by [5] is shown in Figure 2.
obtained by the DTM (method proposed in this work) and those obtained by Hojjati. The resulting graph of the whitedwarfs equation in comparison to the present method and those obtained by [5] is shown in Figure 2.
4. Conclusion
In this work, we presented the definition and handling of one-dimensional differential transformation method. Using the differential transformation, differential equations can be transformed to algebraic equations and the resulting algebraic equations are called iterative equations. This method has applied to solve some class of LaneEmden type equations as a model for the study of the gravitational potential of these degenerate stars (whitedwarfs), which are nonlinear ordinary differential equations on the semi-infinite domain (see [11]). The Figure

Table 1. Comparison between Zhou’s method and SDMM.
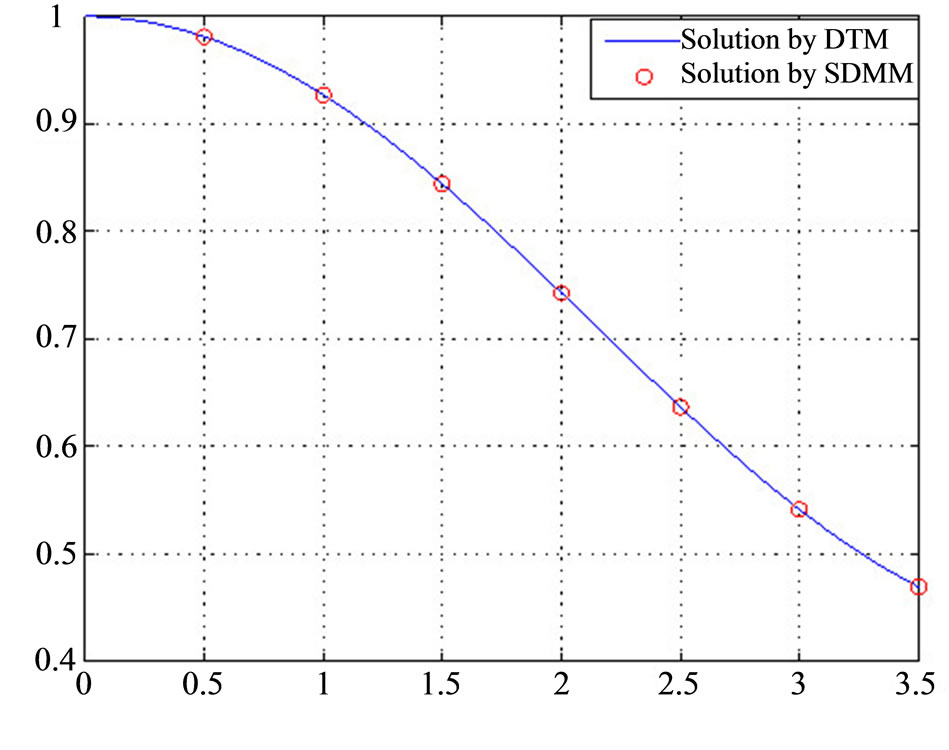
Figure 2. The numerical results  obtained using DTM with C = 0.2.
obtained using DTM with C = 0.2.
2 and table clearly show the high efficiency of DTM to solve nonlinear equations in comparison with other analytical methods equations (see [12,13]).
5. Acknowledgements
The authors gratefully acknowledge the support of the Universidad Tecnológica de Pereira and the group GEDNOL and would like to thank the referee for his valuable suggestions that improved the presentation of the paper.
NOTES