Volatility in High-Frequency Intensive Care Mortality Time Series: Application of Univariate and Multivariate GARCH Models ()
1. Introduction
Mortality time series analyses in the biomedical literature traditionally utilise monthly or yearly aggregates [1] , albeit log-linear (Poisson) approaches to the assessment of the effects of air-borne pollution report daily mortality [2] . The recent application of statistical process control (SPC) to monitor provider (for example intensive care unit, ICU) mortality has seen the use of EWMA (exponentially weighted moving average) charts to plot sequential patient admissions and progressively updated aggregate (mean) mortalities [3] [4] . The data generating process (DGP) of mortality series at this degree of temporal aggregation has not been appropriately characterised and would have implications for performance monitoring strategies such as residual-EWMA control charts, which we have previously advocated [5] . The latter study investigated the DGP of monthly ICU mortality time-series, which displayed autocorrelation, seasonality and (G)ARCH ((Generalised) Autoregressive Conditional Heteroscedasticity) effects. That is, the conditional variance of the time series random component (ϵt, or white noise) followed an autoregressive process with time varying volatility. In the financial time series literature, “volatility” is conventionally equated with (conditional) standard deviation [6] or (conditional) variance [7] , albeit such focus has been subjected to critique [8] [9] . We now extend the previous perspective to daily mortality time series, which, for the current purpose, we will term “high-frequency” and draw inspiration from the paradigm of economic and financial time series [10] [11] . As opposed to financial time series, we do not consider intra-day events [12] [13] [14] on the basis that deaths within a “day” are relatively few in number and occur at irregular time intervals, precluding conventional time series analysis [15] . This being said, the stylised facts of financial “returns”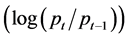
, where 
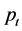is the asset price at time t, [16] have similarities with mortality time series [7] .
We first undertake an analysis of the daily (mean) mortality of an exemplar ICU continuously contributing data (1996-2010) to the ANZICS (Australian and New Zealand Intensive Care Society) adult patient database [17] . In particular: characterisation of the raw series in terms of moments, auto-correlation and ARCH effects; specification of a mean equation and model to remove any linear dependence (for example, ARMA, autoregressive moving average); identification of residual ARCH effects and formulation of a volatility model (in this case, a (G) ARCH model [18] ), and joint estimation of the mean and volatility equations [19] . Secondly, and more ambitiously, we undertake the joint analysis of multiple-provider series on the basis of presumed temporal dependencies [20] . Within a time series paradigm, and inheriting the insights of our first stage analysis, this modelling task presents itself in the domain of multivariate GARCH (MGARCH) models [21] [22] , whereby the dynamics of conditional- variance and covariance of multiple provider-series are estimated; specifically the relations across series in the second order moment. In itself, this task is by no means facile, due to the attendant computational burden of the heavily parameterised MGARCH models [23] .
2. Methods and Materials
2.1. Ethics Statement
Access to the data was granted by the ANZICS (Australian and New Zealand Intensive Care Society) Database Management Committee in accordance with standing protocols; local hospital (The Queen Elizabeth Hospital) Ethics of Research Committee waived the need for patient consent to use their data in this study. The data set analysed was anonymised before release to the authors by the ANZICS Centre for Outcome and Resource Evaluation (CORE) of the Australian and New Zealand Intensive Care Society (ANZICS), custodians of the database. The dataset is the property of the ANZICS Data base and contributing ICUs and is not in the public domain. Access to the data by researchers, submitting ICUs, jurisdictional funding bodies and other interested parties is obtained under specific conditions and upon written request (“ANZICS CORE Data Access and Publication Policy.pdf”, http://www.anzics.com.au/Downloads/ANZICS%20CORE%20Data%20Access%20and%20Publication%20Policy%20July%202017.pdf).
As previously described [5] [24] , the ANZICS adult patient database [17] was utilised to define an appropriate patient set, 1996-(end)2010. Physiological variables collected in accordance with the requirements of the APACHE (Acute Physiology and Chronic Health Evaluation) III algorithm [25] [26] were the worst in the first 24 hours after ICU admission, and all first ICU admissions to a particular hospital for the period 1995-2009 were selected. Records were used only when all three components of the Glasgow Coma Score were provided, records for which all physiologic variables were missing were excluded, and for the remaining records, missing variables were replaced with the normal range and weighted accordingly. Ventilation status in the data base was recorded with respect to invasive mechanical ventilation on or within the first 24 hours of ICU-admission. The mortality endpoint was at hospital discharge. Exclusions: unknown hospital outcome, patients with an ICU length of stay ≤ 4 hours, and patients aged < 16 years of age.
2.2. Mortality Series
1) Exemplar univariate analysis: a running (mean) sum (window, 1 day) of daily mortality was computed over the period 1st January 1996 to 30th December 2010, with a run-in period of calendar year 1995 to establish an average baseline mortality, for ICU site 14.
2) Multivariate analysis: within a single state of the Commonwealth of Australia, for each of the hospital types (rural/regional, metropolitan, tertiary and private), as defined in the ANZICS CORE data dictionary [25] , similar daily mortality series were generated, allowing a minimum 6 month run-in period.
3) The choice of exemplar and multivariate sets was made on the basis of maximizing series length (including run-in period) with no missing values and on this basis was empirical. We have previously noted the problem of missing values in the ANZICS Adult Patient data base [27] .
2.3. Statistical Analysis
Analyses were performed using Stata™ version 14 [28] , the G@RCH™ 7 module [29] of OxMetrics™ 7 statistical software [30] and the “forecast” (V 6.1) package [31] of R (V 3.2.0; 2015) statistical software [32] . Continuous variables were reported as mean (SD), except where otherwise indicated, and statistical significance was ascribed at P ≤ 0.05. Summary statistics of the univariate series were characterised in terms of location (mean), scale (SD), skewness and kurtosis (tail-heaviness) by (i) classical estimators based upon (centred) moments of the distribution and (ii) recently described estimators based upon pairwise comparison of observations; in particular the user written Stata command “robjb” [33] , which provides a robust Jarque-Bera normality test [34] and a robust measure of asymmetry and tail heaviness (“medcouple”; tail heaviness is compared against a value of 0.2 for the standard normal, for both observations smaller (left) and larger (right) than the median). Seasonality was explored using the “tbats” module of the “forecast” package [31] . This module implements an exponential smoothing state space model with Box-Cox transformation, ARMA errors, and trend and seasonal components [35] .
Establishment of daily time-series models at the individual ICU level was based upon classic Box-Jenkins methodology (ARMA models) with investigation of (G)ARCH effects, as previously described [5] [24] . A stationary time series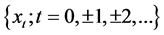 
has an autoregressive moving average (ARMA(p,q)) structure: 
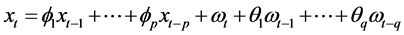where 
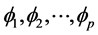are the “autoregressive” (AR) coefficients relating the value of 
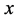at time t to its past p values, and 
are the “moving average” (MA) coefficients, relating the current “white-noise”,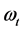 
, to its past q values and
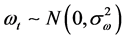. Initial autoregressive integrated moving average model specification (ARIMA; #p, #d, #q, where “#“denotes the lags [p, q] of autocorrelations and moving averages, respectively and the degree of differencing [d]; and “1/4”, say, indicates “1 through 4”) was established using the “auto.arima” function of the R statistical package “forecast” [31] . Volatility of the (squared) residuals 
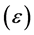of the mean equation (conditional heteroscedasticity [36] ) was checked using the PACF (partial autocorrelation function) of the squared residuals and the user-written Stata™ “armadiag” module [37] , that is, (G)ARCH effects of the error variance process. The latter module, which may be implemented after the “arima”, “arch” or “regress” (ordinary least squares regression, OLS) commands in Stata, plots the residual (standardized residuals with arch) autocorrelations, partial autocorrelations and P-values of the Ljung-Box Q-statistic. For an ARCH model, the variance equation is
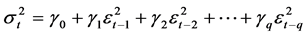, where
, 
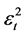are the squared residuals (innovations) and 
are the ARCH parameters; the conditional variance is thus modelled as an AR process. A GARCH (p, q) model includes lagged values of the conditional variance itself 
, where 
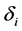are the GARCH parameters (an ARMA process) [5] [24] [38] .
2.4. Univariate Series
Various univariate GARCH models were considered and implemented in Stata™. As originally proposed by Engle [39] , in the ARCH model, the variance of a regression model was modelled as a linear function of the lagged values of the squared regression disturbances. The conditional mean of the series (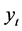
) was given by 
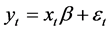(where ![]()
is a linear combination of lagged endogenous and exogenous variables and the (unknown) regression parameters, and ![]()
are the residuals or “innovations”) and the (conditional) variance ![]()
was variously specified and both normal and t (degrees of freedom (df) estimated from the data) distributions were utilised. A (1, 1) lag formulation was utilised for each variant [40] . Other than the vanilla GARCH model [41] , the models assessed were those that formally deal with the stylized facts of financial data such as persistence (the conditional volatility process is not mean reverting), asymmetry (positive and negative shocks have different volatility impacts) and leverage (volatility is increased by negative shocks and decreased by positive) [42] [43] . In particular: the GARCH (p, q) model, as formulated by Bollerslev [41] ; the exponential GARCH (p, q) model of Nelson (EGARCH [44] ); the GJR-(Glosten, Jagaannathan and Runkle [45] )-GARCH model; and the asymmetric power GARCH (APGARCH (p, q)), as described by Ding et al [46] . Full technical details are provided in Appendix 1.
2.5. Multivariate Series
Multivariate GARCH models [21] [22] [47] allow the conditional covariance matrix of the dependent variables to follow a flexible dynamic structure and the conditional mean to follow a vector-autoregressive (VAR) structure [24] . Thus, if {![]()
} is a vector stochastic process of dimension N x 1, and conditioning on past information, then ![]()
ϵ![]()
, where θ is a finite vector of parameters, ![]()
is the conditional mean vector and ϵ![]()
=![]()
; ![]()
is the Cholesky factorisation of the time varying conditional covariance matrix ![]()
and ![]()
is a random innovations vector. Both ![]()
and ![]()
depend on the unknown parameter vector ![]()
(which can be split into two parts, one for ![]()
and one for ![]()
[47] ). MGARCH models differ in specification of![]()
: direct generalisations of the univariate GARCH model of Bollerslev [41] , for instance, the BEKK models [48] ; linear combinations of univariate GARCH models, such as the orthogonal and G(eneralised)O-GARCH [49] [50] models; and conditional correlation models [29] . As noted by van der Weide: “The ‘holy grail’ in multivariate GARCH modeling is without any doubt a parameterization of the covariance matrix that is feasible in terms of estimation at a minimum loss of generality” [51] . For our purposes, the conditional mean ![]()
of these models was of lesser importance and we follow Laurent et al [23] and Tsay [49] and impose a constant conditional mean and consider the conditional covariance matrix ![]()
as the primary objective of investigation [52] . The particular problems of forecasting squared innovations (and determining appropriate loss functions) from MGARCH models, first addressed by Andersen and Bollerslev [53] , reiterated by Laurent et al [23] , and resolved in the concept of realized variance [54] , persuaded us not to undertake multivariate forecasting, which is more appropriate for construction of hedging ratios and portfolio weights [55] [56] [57] and lacks import for mortality series. We therefore considered the conditional correlations between ICUs over time and the ICU conditional variance over time, and contrast the following MGARCH models, using the G@RCH™ 7 module of Oxmetrics™ 7: GO-GARCH [50] ; and the conditional correlation models: constant conditional correlation (CCC) [58] , and dynamic conditional correlation (DCC) [59] . Full technical details are provided in Appendix 2. The program allows specification of different univariate GARCH models within the overall MGARCH process: GARCH, EGARCH, APGARCH and GRJ-GARCH (see above, “Univariate series”) may be selected [47] .
Model selection was guided by a combination of penalized information criteria, assessment of model diagnostics and comparison of model predictive performance. We utilised the Akaike (AIC) and Bayesian (BIC) information criteria (the latter for non-nested comparisons, [60] ; smaller values are advantageous for AIC, with, in general, a difference of >5 indicating potential model discrimination). Model diagnostics: the use of auto- (ACF) and partial-autocorrelation (PACF) function displays, testing for time series stationarity via the KPSS (Kiawtowski-Phillips-Schmidt-Shin) test (null hypothesis of stationarity [61] ) and residual white-noise (Bartlett’s periodogram-based- and Portmanteau (Q)- test) were undertaken after Shumway & Stoffer [62] and as previously described [5] [24] . Lag length for various tests used Schwert’s criterion (a function of sample size) where applicable [63] .
Model performance (univariate series) was assessed by (i) graphical comparison from one-step ahead predictions and dynamic forecasts, the latter (from 1st July 2010 to 31st December 2010) utilising the Kalman filter (see “Dynamic forecasting” in [64] ) and (ii) various loss criteria, using the “accuracy” function of
the R-software “forecast” package: Mean Error (ME, ![]()
, where![]()
); Root Mean Square Error (RMSE,![]()
), Mean Absolute Error (MAE,![]()
); and Mean Absolute Percentage Error (MAPE, ![]()
, where ![]()
[65] . Forecast com-
parison between competing models was assessed by the Stata™ user-written module “dmariano” which computes the Diebold-Mariano comparison of predictive accuracy (for loss criteria MSE, MAE and MAPE [66] ), albeit we note the caution that “… different [GARCH] models can lead to almost equivalent predictive formulas” [7] .
3. Results
The initial data set, 1995-2010, contained 674,193 patient records from 157 ICUs. For the exemplar univariate analysis (ICU site 14), there were 5479 observations over the calendar years 1996-2010, with no missing values. The mean series mortality was 0.17 (0.01) and summary statistics for the raw and first differenced series are seen in Table 1, where tail-heaviness for the first differenced series is noted. Not surprisingly the raw series demonstrated a high degree of autocorrelation to the 100th lag (and beyond, data not shown). The raw series (Figure 1, top panel) displayed a downward mortality trend and rejected the null of stationarity (KPSS test) at all lags (n = 10, p < 0.01). The first differenced series (Figure 1, bottom panel) displayed stationarity at all lag lengths (n = 10, p > 0.1) and the latter series was used for model development, the marked kurtosis being a feature (Table 1). Residuals from OLS regression of the raw series against time displayed autocorrelation and ARCH effects with p-values of the Ljung-Box Q-statistic approximating zero. We were unable to establish season-
![]()
Figure 1. Raw and differenced daily mortality series.
Upper panel: Y-axis, observed daily hospital mortality for ICU site 14. X-axis, time in days. Lower panel: Y-axis, first differenced daily hospital mortality for ICU site 14. X-axis, time in days.
![]()
Table 1. Summary statistics and autocorrelations for raw and first differenced mortality series for ICU site 14.
SD, standard deviation. S-Wilk, Shapiro-Wilk normality test. z, z-statistic. p, p-value. robjb-s, robust Jarque-Bera normality test (skewness). robjb-k, robust Jarque-Bera normality test (kurtosis). medcouple-L, left medcouple (observations less than median). medcouple-R, right medcouple (observations greater than median). Tail-heaviness (medcouple) is compared with a value of 0.2 for the standard normal.
ality of the (raw) series at the monthly or yearly level using the “tbats” module of the R-software “forecast” package.
The model formulated by the “auto-arima” module of the R-software “forecast” package [31] was ARIMA (1/4, 1, 1/3). Alternate specifications up to ARIMA (1/9, 1, 1/3) were considered, but such extensive parameterisation of the mean dynamic was considered to lack interpretation and a simpler mean model, ARIMA (7, 1, 0) was chosen to reflect the daily series (additive seasonality), albeit the latter model and all other ARIMA variants demonstrated substantial ARCH effects. Of the 8 GARCH models initially considered, an asymmetric power (G)ARCH model (APGARCH, [46] [67] ) with t-distribution (df, 11.63) and ARMA (7, 0) for the mean-model, was the most parsimonious and, not surprisingly, had substantial information criterion advantage over the ARIMA mean model (ARIMA (7, 1, 0)); BIC −86,324 versus −73,873. Information criteria (AIC and BIC) with model and estimated t df for all univariate GARCH models are detailed in Table 2. For each of the GARCH variants, a t-distribution had information criterion advantage, but between-model differences based upon BIC were rather modest. Graphical display of ARCH specification tests for each of the t-distribution variants is seen in Figure 2. The APGARCH-t model (lower right panel) appeared the most parsimonious, especially with regard to the lack of residual (![]()
) serial correlation, as indicated by the lag p-values (?0.05) of the (Ljung-Box) Q-statistic [68] . APGARCH parameter estimates are shown in Table 3 (cross-referenced to model formula in Statistical analysis, Univariate series (iii), above), the scalar sum of α and β (=1.002) suggesting persistence of conditional volatility. Conditional variance plots (Figure 3) from the APGARCH-t model exhibited extreme volatility during the period 1996-1998 (upper panel) and substantial, but declining volatility, from 1998-2010 (lower panel). This being said, a “level” shift (coded 1/0) at 1st January 1998 lacked significance (p = 0.23). The predictive performance of the APGARCH-t model was also considered. One-step-ahead predictions are seen in Figure 4 (upper panel), demonstrating, not surprisingly, virtual identity of the raw series signal and the one- step predictions (Table 4). The dynamic 6-month forecast is shown in Figure 4 (lower panel), with some divergence between the raw series and forecast, reflected in the increment of the MAPE loss function for the out-of sample forecast, 2nd June 2010 to 31st December 2010 (Table 4(a), third column). With respect to comparative predictive accuracy between GARCH variants (in particu-
df, degrees of freedom. −t, t distribution. t-df, estimated t degrees of freedom, EGARCH model, no convergence.
![]()
Figure 2. ARCH specification tests for GARCH models.
Upper left panel: GARCH (1, 1) model, t-distribution. Upper right panel: EGARCH (1, 1) model, t-distribution. Lower left panel: GJR-GARCH (1, 1) model t-distribution. Lower right panel: APGARCH (1, 1), t-distribution. 95% CB, 95% confidence bands. Q-stat, Ljung-Box Q-statistic [80] . ARCH param, ARCH parameters.
![]()
Table 3. Parameter estimates of the APGARCH-t model.
L, lag. t-df, estimated t degrees of freedom.
![]()
Figure 3. APGARCH-t conditional variance plots.
Upper panel: 1996-2010, Y-axis, one-step conditional variance. X-axis, time (days); Lower panel: 1998-2010, Y-axis, one-step conditional variance. X-axis, time (days).
![]()
![]()
(a)Dec., December. Jan., January.
(b)MSE, means squared error. MAE, mean absolute error. MAPE, mean absolute percentage error; Significant p-values indicate superior APARCH-tforecast performance.
Table 4. (a) Forecast evaluation of APGARCH-t model. (b) Comparative forecasts.
![]()
Figure 4. APGARCH-t model: One step prediction and dynamic forecast.
Upper panel: One-step ahead predictions for the APGARCH-t (mean) model; Y-axis, mortality; X-axis, time (days); Lower panel: Six month dynamic forecast for APGARCH-t (mean) model; Y-axis, mortality; X-axis, time (days).
![]()
Figure 5.. Multivariate rural/regional, metropolitan, tertiary and private series.
Hospital raw mortality (Y-axis) plotted against time (days) for various sites in the multivariate series: upper left, rural/regional; upper right, metropolitan; lower left, tertiary; lower right, private.
lar, using the t distribution): for a maximum lag of 32 (chosen by Schwert criterion [63] , with a uniform kernel to calculate long-run variance) a variable superiority of the APGARCH-t forecasts (compared with GARCH-t, EGARCH-t and GJR-GARCH-t) was demonstrated, as indicated in Table 4(b), test significance being dependent upon the particular loss criterion [69] . Compared with the conventional ARIMA (7, 1, 0) model, the APGARCH-t demonstrated a superior forecast (MAPE, p = 0.015; MAE, p = 0.026).
The four multivariate component raw series (rural/regional, metropolitan, tertiary and private) are seen in Figure 5, demonstrating varied levels of, and trend decline in, mortality. The series are further characterised in terms of summary statistics and autocorrelations for raw and differenced series in Table 5 and Table 6 respectively. The most notable findings were (i) marked kurtosis and rejection of normality for both the raw and differenced series, and (ii) for each of the multivariate series, the raw series rejected the null of stationarity (KPSS test) at all lags (n = 10; p < 0.01) and the first differenced series displayed stationarity at all lag lengths (n = 10; p > 0.1). The 3 MGARCH model variants (GO-GARCH (normal distribution only), CCC (normal and t-distribution) and
![]()
Table 5. Summary statistics for rural/regional, metropolitan, tertiary and private multivariate series.
SD, standard deviation. S-Wilk, Shapiro-Wilk normality test. z, z-statistic. p, p-value.
![]()
Table 6. Autocorrelations of raw and first differenced mortality series for rural/regional, metropolitan, tertiary and private multivariate series.
![]()
Table 7. Model specifications for the MGARCH series.
GO-GARCH: generalised orthogonal GARCH. CCC: constant conditional correlation. DCC: dynamic conditional correlation. -normal: normal distribution. ?t: t distribution (estimated from the data)
DCC (normal and t-distribution)), displayed varying degrees of convergence difficulties, especially with the 7 component univariate series of the tertiary multivariate set. Table 7 shows model information criteria (AIC and BIC) for (i) two univariate specifications, GARCH (1, 1) and APGARCH (1, 1) and (ii) the 4 MGARCH series (rural/regional, metropolitan, tertiary and private). Within each MGARCH series no model specification dominated, although there was some advantage for the t-distribution in the private series. The tertiary series allowed only a univariate GARCH specification and the GO-GARCH model was unable to converge with the univariate APGARCH. Graphical analysis is presented of the conditional correlations and variances from the DCC-t model (univariate APGARCH (1, 1)), except for the tertiary series (univariate GARCH (1, 1)). Figure 6 & Figure 7 show the conditional correlations between the univariate series of the rural/regional and metropolitan series. The correlations between the component univariate series were quite variable, and demonstrated reversion to a constant level (see Statistical analysis, Multivariate series, ii(b), above), the private series being noted for relatively high positive correlation (0.27 - 0.85). The variances of the component series of each of the multivariate series demonstrated a variable rate of time decline from periods of early volatility and volatility spikes in the rural/regional and metropolitan and private series during the calendar years mid 2006-2007 to mid 2007-2008.
4. Discussion
The current study has demonstrated that high frequency (daily) mortality series
![]()
Figure 6. Conditional correlations between the ICU sites (32, 49, 52 and 106) of the rural/regional multivariate series.
Conditional correlations (Y-axis) over time (X-axis) for various combinations of ICU sites.
![]()
Figure 7. Conditional correlations between the ICU sites (37, 64, 73 and 130) of the metropolitan multivariate series (obtained from a variant of the DCC model: Asymmetric Corrected Dynamic Correlation Model (Aielli) [59] , with univariate APGARCH (1, 1).
Conditional correlations (Y-axis) over time (X-axis) for various combinations of ICU sites.
exhibit (G)ARCH effects, consistent with our two previous studies of the same data-base [5] [24] , albeit the specific models differ, most likely reflecting different temporal data aggregation, daily versus monthly [70] . Thus, unlike some financial data, for example exchange rates, the ability to discern ARCH effects did not decrease with increasing sampling interval [71] .
In financial time series, conditional asymmetry is a stylized fact [67] . That is, there is a negative correlation between the squared current innovations ![]()
and the past innovations, or empirically, the volatility due to, say, a price decrease is greater than that of a comparable price increase. For classical GARCH, the conditional variance is a function of the modulus of the past![]()
, positive ![]()
and negative ![]()
innovations having the same effect on current volatility: ![]()
where Cov = covariance. Under conditions of second-order stationarity, ![]()
may be decomposed as ![]()
where ![]()
is an iid sequence and ![]()
is a measurable positive function of the past of![]()
. The circumstance ![]()
is that of a leverage effect. For the APGARCH model (see Statistical analysis, Univariate series, (iii)), if ![]()
then “… negative innovations have more impact on current volatility than positive ones of the same modulus” [67] ; that is, there exists a leverage effect. This condition was satisfied in the current APGARCH model (![]()
= 0.330, ![]()
was significantly different from 0, P = 0.000, Table 3).
However, a degree of caution is required in considering the application of asymmetric volatility models [43] to non-economic/financial data. Such models require “…a specification that can accommodate a leverage effect” [40] , such specification being described as “crucial” by the authors of the APGARCH model [46] . We make two points with regard to leverage in the current series: (i) a snapshot of the series, 1996-1998, raw versus the differenced mortality (Figure 8), is suggestive of volatility clustering during sharp falls in mortality, similar to that described by Engle for financial data [72] and (ii) the early volatility maybe at least in part due to reporting artefacts or processes at that time, in addition to the increased variability associated with smaller numbers. The overall trend then is for declining mortality, which would be confounded with improvements in reporting processes, data completeness and increasing numbers. This would suggest that we are not seeing a leverage effect as such, but rather a confluence of trends.
The implications of a volatility model perspective [43] in the context of mortality rates are best considered against the background of (i) the above perspective of the financial paradigm where the trade-off between risk and expected return is a fundamental concern and the measurement and forecasting of volatility a core pursuit [73] and (ii) recent actuarial and demographic literature, where detailed comparisons between (G)ARCH?based stochastic mortality models and the orthodox Lee-Carter model [74] , have favoured the former. Of interest, the literature review (section 2.3) of Andersen et al., “Volatility forecasting in fields outside finance” in 2006 [73] made no specific mention of mortality series. The
![]()
Figure 8. Raw mortality and differenced mortality series: 1996 to 1998.
Upper panel: raw series 1996-1998; Y-axis, raw mortality; X-axis, time (days); Lower panel: differenced series 1996-1998; Y-axis, differenced mortality; X-axis, time (days).
original Lee-Carter model (modelling the logarithm of the central death rate ![]()
for age x at time t) used ARIMA functions to undertake mortality forecasts, but assumed homoscedasticity and constant volatility, which assumptions are belied by the structure of long-term (yearly) mortality series which demonstrate non-stationarity, conditional heteroscedasticity and non-normality [75] [76] . Thus, apposite analysis of mortality time-series mandates the demonstration and appropriately modelling of volatility. As opposed to the population perspective of demography, we model the mortality of the critically-ill, where the interplay of an ensemble of patient factors (severity of illness, patient type) and provider characteristics (ICU occupancy, structure and staffing), not all of which are in principle identifiable, are determinate in the conditional heteroscedasticity of the mortality series.
The parsimony of univariate GARCH models has been shown in actuarial and demographic studies, but the analysis of, say, cross-(nation)-state mortality correlations [75] within the same framework has been “…a largely unchartered territory” [77] . To this end, the recent study of Gao and Hu [78] reports 8 separate GARCH (1, 1) models in a sub-section “An application to multi-country study”, rather than a multivariate approach. Although not undertaking MGARCH forecast assessment in the current series (see Statistical analysis, Multivariate series; above), recent evidence has suggested primacy of the DCC model, at least in financial series [23] [56] and further sophisticated variants of the DCC model have been presented [79] , although cautions about the DCC representation have been expressed [80] . In a wide ranging study of time series from finance, physiology and genomics, Podobnik et al., using time-lag random matrix theory, demonstrated that “… cross-correlations are ubiquitously present in many systems … [and] … studying these cross-correlations is a necessary prerequisite for understanding them …” [81] . Similar studies have been presented from the social sciences [82] [83] . As the selection of univariate series was based upon defined provider categories of hospital type and locality, there was an expectation of substantial but variable levels of correlation between these (multivariate) series, more so given the particular structure of critical care practice in Australia and New Zealand (uniform training scheme and closed ICUs [84] ). The conditional correlations were surprisingly low (<0.1) between tertiary series and substantial (0.4 - 0.6) between rural-regional and private series. An explanation for this finding could be the similarity / uniformity of patient-mix and treatments in tertiary ICUs. Thus, condition correlations would look relatively independent, as opposed to the cross-correlations, which would be expected to be related. Such explanation would also suggest that other sets of hospitals were more heterogeneous, which seems plausible, although less so for the metropolitan centres. Conditional variance volatility demonstrated, not surprisingly, persistence and the degree of volatility was most marked in non-tertiary series where annual patient admission numbers were lower [85] . Within the statistical process control (SPC) paradigm, where we have demonstrated the facility of univariate GARCH modelling [5] , the extension to “… monitor [ing] outcomes at more than one unit simultaneously” has been advocated [86] and, on the basis of the cross- correlations revealed in the current analysis, would also appear to have a plausible empirical basis.
5. Conclusion
High frequency ICU mortality time series display autocorrelation, persistence of conditional variance and volatility which are appropriately modelled using estimators which explicitly account for these attributes. Similarly, multivariate mortality series exhibit these stylised facts and temporal dependencies, reflected in varying degrees of conditional correlations which belie the use of (repeated) univariate approaches to the understanding of the performance of sets of ICUs.
Appendix 1
i) The GARCH(p,q) model, as formulated by Bollerslev [41] ;
![]()
, where ![]()
are constants and ![]()
are the squared residuals (innovations:![]()
). This model is an obvious comparator and in some financial data (exchange rates) it outperforms more sophisticated models [40] .
ii) The exponential GARCH(p,q) model of Nelson (EGARCH [44] ).
![]()
; where the ![]()
parameter indicates leverage ![]()
[42] . Different formulations and software implementations of the EGARCH model exist and we provide a minimal equation where p = q = 1 [87] .
iii) The GJR-(Glosten, Jagaannathan and Runkle [45] )-GARCH model;
![]()
, where ![]()
is a dummy variable of
value 1 when ![]()
is negative and 0 otherwise and the model assumes that the sign of ![]()
(positive or negative) is determinant of the impact of ![]()
on the conditional variance ![]()
[88] .
iv) The asymmetric power GARCH (APGARCH (p, q)), as described by Ding et al [46] ;
![]()
, where ![]()
and![]()
. The δ parameter performs a Box-Cox type transformation of st and ![]()
reflects the “leverage” effect [89] ; ![]()
is a non-restrictive identifiability constraint [67] . If the sum of (scalar) α and β (a persistence coefficient [90] [91] ) < 1, the conditional volatility process is mean reverting and shocks are transitory. First published in 1993, this is an encompassing model to the extent that it includes the ARCH, GARCH and GJR-GARCH models as special cases [88] .
Appendix 2
i) GO-GARCH [50] . In orthogonal GARCH models, the observed data are assumed to be generated by an orthogonal transform of N (or
) are linked to unobserved, uncorrelated factors (![]()
; in GO-GARCH, equal to the series number) through a linear, invertible transformation (![]()
, a non-singular ![]()
matrix). The conditional covariance matrix of ![]()
is
expressed as![]()
, where ![]()
are the columns of ![]()
and ![]()
are the diagonal elements of ![]()
[22] .
ii) Conditional correlation models: use nonlinear combinations of univariate GARCH models to represent the conditional covariances, which are decomposed into conditional variances and correlations. The diagonal elements of ![]()
(the conditional covariance matrix) are modelled as univariate GARCH models, whereas the off-diagonal elements are modelled as nonlinear functions of the diagonal terms.
a) constant conditional correlation (CCC) [58] ; here the conditional correlations are (time) invariant and the conditional covariances are proportional to the product of corresponding standard deviations. The series (![]()
) are modelled as![]()
. Although we estimate the CCC model, it is used as a comparator as the “… hypothesis of CCCs is not tenable except for specific cases and short periods” [92] .
b) dynamic conditional correlation (DCC) [59] . The CCC model is generalised such that the conditional correlations change over time:![]()
, where the diagonal elements ![]()
follow univariate GARCH processes and ![]()
follows a time-varying dynamic process. A constraint of this model is that “… all correlations have the same dynamic pattern… [and] … revert to a constant level” [92] .
![]()
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/
Or contact ojapps@scirp.org