The Density of Energy States for Nonparabolic Dispersion Law in a Strong Magnetic Field ()
1. Introduction
In a study of the energy spectra of electrons in semiconductors and metals exceptional role has played the application of quantizing magnetic fields. In the works of [1] the temperature dependence of the density of states in quantizing magnetic fields were considered as the result of thermal broadening of the Landau levels. In those works studies showed, that the density of states of the continuous spectrum measured at the temperature of liquid nitrogen at low temperatures turns into discrete Landau levels. However, in these works are considered only in the quadratic dispersion law.
The aim of this work is to determining the temperature dependence of the density of energy states in a quantizing magnetic field for the model Kane and into the effect of temperature of a sample on the results of treatment of experimental data.
2. Determination of the Density of Energy States in a Quantizing Magnetic Field for the Kane Dispersion Law
In a magnetic field the energy of free electrons with a quadratic dispersion law, and in view of the spinal level splitting energy takes the following form [2]:
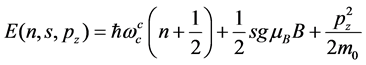 (1)
(1)
In a magnetic field density of states for a parabolic band is determined by the following expression
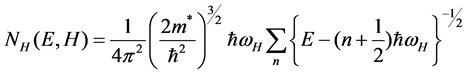 (2)
(2)
However, if the energy dependence of the wave vector is not described by a quadratic form, such as, for electrons in InSb energy levels of the charge carriers in the magnetic field is not equidistant, since cyclotron mass determined by the expression
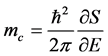 (3)
(3)
and therefore the cyclotron frequency depends on Е and kz.
Nonparabolicity conduction band in compounds III-IV and II-VI is the result of interaction between the conduction and valence bands three. In magnetic field energy levels for the three bands (apart from the heavy hole band that does not interact with them) are cubic equation [3] [4]:
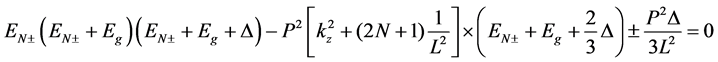 (4)
(4)
Here,  -energy electrons in the conduction band in view of spin in a quantizing magnetic field,
-energy electrons in the conduction band in view of spin in a quantizing magnetic field,  -width band-gap,
-width band-gap, 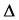 -the spin-orbit splitting, P-the matrix element.
-the spin-orbit splitting, P-the matrix element.
From this condition of the cubic Equation (4) reduces to the square, the solution of which electrons of the conduction band is given by
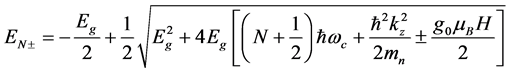 (5)
(5)
Equation (5) is applicable only for narrow-gap semiconductors.
From Equation (5) we define kz without spin:
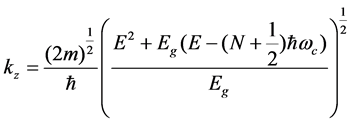 (6)
(6)
We return now to the calculation of the density of states with a nonparabolic dispersion law in a magnetic field. The movement of free electrons along the z axis and is quantized by kz. That is,
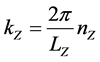 (7)
(7)
According to the expression (6) and (7) the number of states the energy interval from
 to E:
to E:
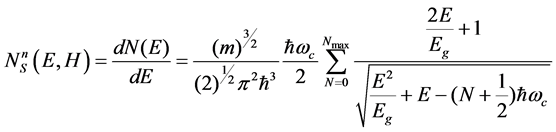 (10)
(10)
Here, 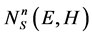 -the density of the energy states of a Kane dispersion law in a quantizing magnetic field. At
-the density of the energy states of a Kane dispersion law in a quantizing magnetic field. At 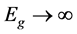 expression (10) goes into a parabolic dispersion law (2). In this expression, the temperature-induced broadening of the energy levels is disregarded.
expression (10) goes into a parabolic dispersion law (2). In this expression, the temperature-induced broadening of the energy levels is disregarded.
Thermal broadening of the levels in a magnetic field gives rise to the smoothing of discrete levels. Thermal broadening is to be taken into account using a derivative of the
energy distribution function of the Fermi-Dirac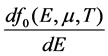 . At absolute zero of temperature, the
. At absolute zero of temperature, the  function transforms into the delta-function of Dirac.
function transforms into the delta-function of Dirac.
In order to take into account the temperature dependence of the density of states, we
expend 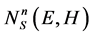 into series with respect to
into series with respect to 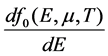 functions (Figure 1).
functions (Figure 1).
We then obtain the density of energy states depending on temperature [1] (Figure 1):
![]() (11)
(11)
![]()
Figure 1. Determination of the change in the density of energy states with decreasing temperature in high magnetic fields using the Kane model.
The corresponding expression at ![]() transforms into (10).
transforms into (10).
3. Conclusion
We developed a new method for determining the density of the energy states in a quantizing magnetic field for the Kane model. For a nonquadratic dispersion law was shown that the density of states in a strong magnetic field at an increased temperature coincides with the density of states in the sample without a magnetic field.