Gerber Shiu Function of Markov Modulated Delayed By-Claim Type Risk Model with Random Incomes ()
1. Introduction
Analyzing a risk model using the Gerber-Shiu discounted function largely promoted the theory and provided a useful tool for the computation of many performance measures. As a classical risk model is too idealistic, in fact there are a lot of distracters, it has become necessary to study risk models having parameters governed by the external environment. Recently many authors considered risk models having Markov modulated environment or Markovian regime-switching models. The purpose of this generalization is to enhance the flexibility of the model parameters for the classical risk process. For a Markov modulated Poisson process, the arrival rate varies according to a given Markov process. The risk models managed by an insurance company are a long-term program and system parameters such as interest rates, premium rates, claim arrival rates, etc. may need to change whenever economic or political environment changes. So it is always preferable to regulate the model according to the external environment.
The assumption on independence among claims is an important condition used in the study of risk models. However, in many practical situations, this assumption is inconsistent with the operation of insurance companies. In reality, claims may be time- correlated for various reasons, and it is important to study risk models which can also depict this phenomenon. Two types of individual claims, main claims and associated by-claims are introduced, where every by-claim is induced by the main claim and could be delayed for one time period depending on the amount to be paid towards the main claim. Further, we discuss the model in the presence of random incomes in order to accommodate insurance companies having lump sums of income occurring time to time based on their business and other related activities.
The idea of delayed claims is gaining importance due to its relevance in many real world situations. Xie et al. [1] considered the expected discounted penalty function of a compound Poisson risk model with delayed claims and proved that the ruin probability for the risk model decreases as the probability of the delay of by-claims is increasing, while in [2] the authors discussed the model perturbed by diffusion. The same authors in [3] presented an explicit formula for the ruin probability when the claims were delayed. Delayed claim risk models were first introduced by Waters et al. [4] so that the independence assumption between claim sizes and their interarrival times can be relaxed and since then it has been investigated by many researchers. Hao et al. [5] analyzed the risk model with delayed claims in a financial market where the probability of delay of each claim is constant and independent of claim amounts.
Yu [6] studied the expected discounted penalty function in a Markov Regime- Switching risk model with random income. Assuming that the premium process is a Poisson process, Bao [7] obtained the Gerber-Shiu function of the compound Poisson risk model. In this paper the author discussed the ruin model in which the premium is no longer a linear function of time but a Poisson process. Zhu et al. [8] considered the expected discounted penalty function of a compound Poisson risk model with random incomes and potentially delayed claims. Huang and Yu [9] investigated the Gerber-Shiu discounted penalty of a Sparre-Andersen risk model with a constant dividend barrier in which the claim inter-arrival distribution is the mixture of an exponential distribution and an Erlang (n) distribution.
J. Gao and L. Wu [10] considered a risk model with random income and two types of delayed claims and derived the Gerber-Shiu discounted penalty function using an auxiliary risk model. This was done as an extension of the work by Xie et al. in [1] and [2] . More developments about compound Poisson models can be found in Hao and Yang [11] where they analyze the expected discounted penalty function of a compound Poisson risk model with random incomes and delayed claims. In this paper, we investigate a general form of such a risk model by assuming the existence of Markovian environment.
The rest of this paper is organized as follows. In Section 2, we describe the risk model considered. In Section 3, the integral equations for the expected discounted penalty function are obtained. Section 4 deals with the case with exponential random incomes and Laplace transforms of the discounted penalty function derived. In Section 5, we illustrate the usefulness of the model by computing probability of ruin for a model having only two states and in Section 6 a risk model without any external environment. Section 7 concludes the paper.
2. The Risk Model
Here we consider a continuous time risk model with random incomes, two types of insurance claims, namely the main claims and the by-claims, and where the parameters are depending on the external environment. Let 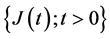 be the external environment process which is assumed to be a homogenous irreducible and recurrent continuous time Markov chain with finite state space
be the external environment process which is assumed to be a homogenous irreducible and recurrent continuous time Markov chain with finite state space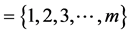 , intensity matrix
, intensity matrix
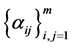 and
and 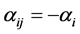 for
for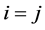 .
.
Let  and
and 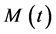 be respectively, the number of claims and the random incomes occurring in
be respectively, the number of claims and the random incomes occurring in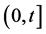 . Let
. Let  be the epoch of the nth claim and
be the epoch of the nth claim and 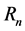 be the epoch of the nth random premium. When
be the epoch of the nth random premium. When 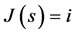 for all s in a small interval
for all s in a small interval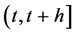 , the number of claims occurring in that interval is assumed to follow the Poisson distribution with parameter
, the number of claims occurring in that interval is assumed to follow the Poisson distribution with parameter 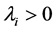 and the nth main claim amount
and the nth main claim amount 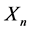 has the distribution function
has the distribution function , density function
, density function 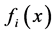 and finite mean
and finite mean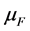 . Also the number of random premiums follows the Poisson distribution with parameter
. Also the number of random premiums follows the Poisson distribution with parameter 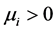 and the nth premium amount
and the nth premium amount ![]() having the distribution
having the distribution![]() , density function
, density function ![]() and finite mean
and finite mean![]() . Each main claim will generate a by-claim
. Each main claim will generate a by-claim ![]() and when
and when![]() , let
, let ![]() be the distribution function of the by-claim amount,
be the distribution function of the by-claim amount, ![]() the density function and the finite mean
the density function and the finite mean![]() . These
. These![]() ,
, ![]() and
and ![]() are assumed to be iid positive random variables and are independent of each other. Moreover, the processes
are assumed to be iid positive random variables and are independent of each other. Moreover, the processes![]() ;
; ![]() and
and ![]() have independent increments.
have independent increments.
The processes ![]() and
and ![]() are Markov-modulated Poisson processes, which are special cases of the Markovian Arrival Process (MAP). The claim arrival rates, claim amounts, income arrival rates and random incomes are all driven by the external environment process
are Markov-modulated Poisson processes, which are special cases of the Markovian Arrival Process (MAP). The claim arrival rates, claim amounts, income arrival rates and random incomes are all driven by the external environment process![]() .
.
In this paper, we consider the risk model having the following claim occurrence process. There will be a main claim ![]() at every epoch
at every epoch ![]() of the Poisson process and this will induce a by-claim
of the Poisson process and this will induce a by-claim ![]() . Moreover if the main claim amount
. Moreover if the main claim amount ![]() is less than the threshold level
is less than the threshold level![]() , then both the main claim
, then both the main claim ![]() and associated by-claim
and associated by-claim ![]() occurs simultaneously. If the main claim amount
occurs simultaneously. If the main claim amount ![]() is larger than or equal to the threshold
is larger than or equal to the threshold![]() , then the occurrence of the by-claim
, then the occurrence of the by-claim ![]() is delayed to the next claim epoch
is delayed to the next claim epoch![]() . If the occurrence of the by-claim
. If the occurrence of the by-claim ![]() is delayed to
is delayed to![]() , then the delayed claim
, then the delayed claim ![]() and the main claim
and the main claim ![]() occur simultaneously.
occur simultaneously.
In this set up, the surplus process ![]() of the risk model is defined as
of the risk model is defined as
![]() (1)
(1)
where u is the initial capital and ![]() is the sum of all by-claims
is the sum of all by-claims ![]() that occurred upto time t. Define the time of ruin by
that occurred upto time t. Define the time of ruin by![]() . The ruin probabilities given initial capital u are
. The ruin probabilities given initial capital u are ![]() . Let
. Let ![]() and
and ![]() be the surplus immediately before ruin and the deficit at ruin respectively. The Gerber- Shui discounted penalty function is of the form
be the surplus immediately before ruin and the deficit at ruin respectively. The Gerber- Shui discounted penalty function is of the form
![]()
where ![]() is the discounted factor,
is the discounted factor, ![]() is the penalty function and
is the penalty function and ![]() is the indicator function of the event A.
is the indicator function of the event A.
The safety loading condition is
![]()
Now let us consider an auxiliary risk model, which is same as the one described above with a slight change assumed at the first claim epoch. Instead of having one main claim ![]() and a by-claim
and a by-claim ![]() with probability
with probability ![]() at the first epoch
at the first epoch![]() , we have another by-claim Y added at the first epoch
, we have another by-claim Y added at the first epoch![]() . i.e.; by-claim Y and the main claim
. i.e.; by-claim Y and the main claim ![]() occur at
occur at ![]() simultaneously. Hence the corresponding surplus process
simultaneously. Hence the corresponding surplus process ![]() of this auxiliary risk model is defined as
of this auxiliary risk model is defined as
![]() (2)
(2)
where Y denotes the other by-claim amount added at the first claim epoch and let![]() . Assume that Y and
. Assume that Y and ![]() are iid positive random variables. Let
are iid positive random variables. Let ![]() denote the Gerber-Shiu discounted penalty function that can be defined for the auxiliary model corresponding to the initial environment
denote the Gerber-Shiu discounted penalty function that can be defined for the auxiliary model corresponding to the initial environment![]() .
.
3. System of Integral Equations
We are interested in the Gerber-Shiu discounted penalty function of the model. Analyzing the surplus process ![]() in a small interval
in a small interval![]() , for
, for![]() , we have the following cases:
, we have the following cases:
1) During ![]() no claim occurs, no premium arrivals and no change in the external environment.
no claim occurs, no premium arrivals and no change in the external environment.
2) During the time interval![]() , one main claim and a by-claim occurs, main claim is less than the threshold level, no premium arrival and no change in the external environment.
, one main claim and a by-claim occurs, main claim is less than the threshold level, no premium arrival and no change in the external environment.
3) One main claim and a by-claim occurs in![]() , main claim is more than the threshold level (this transfers by-claim amount to the next claim point), no premium arrival and no change in the external environment.
, main claim is more than the threshold level (this transfers by-claim amount to the next claim point), no premium arrival and no change in the external environment.
4) No claim occurs in ![]() but one premium arrival and no change in the external environment.
but one premium arrival and no change in the external environment.
5) No claim occurs, no premium arrival in ![]() but a change in the external environment in
but a change in the external environment in![]() .
.
6) All other events having total probability![]() .
.
The Gerber-Shiu discounted penalty function of the model satisfies equation,
![]() (3)
(3)
Similarly, for the auxiliary model we have
![]() (4)
(4)
Expanding![]() , dividing by t and taking as limit
, dividing by t and taking as limit ![]() in (3) and (4) we get,
in (3) and (4) we get,
![]() (5)
(5)
![]() (6)
(6)
Substituting![]() ,
,
![]() ,
,
![]()
and![]() ;
;
in the Equations (5) and (6). They reduce to,
![]() (7)
(7)
For the auxiliary model, it is
![]() (8)
(8)
where![]() ,
,
![]()
and
![]() .
.
Remark 1: Letting ![]() and
and![]() , above expressions will give the Laplace transform of time to ruin.
, above expressions will give the Laplace transform of time to ruin.
![]()
![]()
Remark 2: Letting ![]() and
and![]() , the ruin probabilities for the model is obtained.
, the ruin probabilities for the model is obtained.
Remark 3: Letting![]() , we get the discounted expectation of the deficit at ruin for the model.
, we get the discounted expectation of the deficit at ruin for the model.
4. Laplace Transform of Gerber-Shiu Function for the Model with Exponential Incomes
This section assumes that the random premium amounts are exponentially distributed and we derive the Laplace transform of the Gerber-Shiu function.
Writing ![]() as the Laplace transform of
as the Laplace transform of![]() ,
,
i.e.
![]()
we have,
![]() (9)
(9)
where
![]() ,
,
![]() and
and
![]()
Similarly for the auxiliary model we have,
![]() (10)
(10)
where
![]() and
and
![]() .
.
Suppose that the random income ![]() are exponentially distributed (i.e.)
are exponentially distributed (i.e.) ![]() .
.
Then we have,
![]()
![]()
Hence,
![]()
and
![]()
Further simplifying we have,
![]() (11)
(11)
and
![]() (12)
(12)
5. Explicit Results for a Two-State Model with Exponential Claims and Degenerate Threshold
We consider the case where all the by-claims are delayed to the next claim epoch and both claim amounts are exponentially distributed, i.e.; the distribution functions are
![]() and
and![]() . Also let
. Also let ![]() (only two external environment states).
(only two external environment states).
The probability of ruin is obtained by putting ![]() in Equations (11) and (12).
in Equations (11) and (12).
We have,
![]() ;
;![]() ;
;![]() ;
;![]() ;
;
![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() .
.
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
![]() . (16)
. (16)
Numerical example 1: Let![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
; ![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() .
.
Then we have![]() . Table 1 shows the ruin probabilities of the example and further Figure 1 and Figure 2 show the ruin probabilities for different values of u.
. Table 1 shows the ruin probabilities of the example and further Figure 1 and Figure 2 show the ruin probabilities for different values of u.
![]()
Table 1. Ruin probabilities for the model in numerical example 1.
![]()
Figure 1. Example 1: Ruin probabilities for initial state 1.
![]()
Figure 2. Example 1: Ruin probabilities for initial state 2.
One can note from the graph that in Figure 1, ![]() and
and ![]() decrease sharply when u is in
decrease sharply when u is in ![]() and then turns flat as u increases. The same observation is made in Figure 2 for
and then turns flat as u increases. The same observation is made in Figure 2 for ![]() and
and![]() .
.
6. Explicit Results for the Model with Exponential Claims and No External Environment
In this section, we consider the risk model without external environment (i.e.; ![]() and all the other assumptions remaining the same as in Section 5. Resulting equations for the ruin probabilities are,
and all the other assumptions remaining the same as in Section 5. Resulting equations for the ruin probabilities are,
![]() (17)
(17)
![]() (18)
(18)
where![]() .
.
Numerical example 2: Let![]() . From Table 2, we can see the behavior of ruin probabilities in this model.
. From Table 2, we can see the behavior of ruin probabilities in this model.
Figure 3 shows the ruin probabilities in Example 2 for different values of u. One can see that, ![]() and
and ![]() decreases sharply when u is in
decreases sharply when u is in ![]() and then turn flat when u increases further.
and then turn flat when u increases further.
7. Conclusions
In this paper, we investigated a Markov-modulated risk model with random incomes
![]()
Table 2. Ruin probabilities for the model in numerical example 2.
![]()
Figure 3. Example 2: Ruin probabilities.
and two types of claims (i.e., main claims and by-claims) and where the by-claims may be delayed to the next claim point. We assume that the by-claim can be delayed depending on the corresponding main claim amount; whether it is exceeding the random threshold. All system parameters are assumed to be depending on the state of the external environment. System of integral equations for the Gerber-Shiu penalty function was obtained. Then we obtained Laplace transforms of the penalty function under the assumption that the random incomes follow an exponential distribution. Next for a simplified model with exponential claim amounts, we presented expressions for the probability of ruin and some numerical illustrations included. Finally we considered another simplified model in the absence of external environment and numerically illustrated the influence of initial capital on the ruin probabilities.
Future research includes investigation of the risk model with generalized distributions. It would be also interesting to find other ruin related parameters like surplus prior to ruin, deficit at ruin, etc.
Conflict of Interests
The authors declare that there is no conflict of interests regarding the publication of this paper.