Local Curvature and Centering Effects in Nonlinear Regression Models ()
Received 15 December 2015; accepted 20 February 2016; published 23 February 2016

1. Introduction
Applied probability models are mathematical constructs that have roots in both theory and observed data. They often reflect specific theoretical properties, but may simply be the application of an all-purpose linear model. The fitting of a probability model to the observed data requires careful consideration of potential difficulties and model sensitivities. These may include aspects of the model itself or anomalies in the structure of the database. As large scale observational databases have become more common, the possibility of unplanned and non- standard data patterns have become more common.
The stability of linear models can be affected by various properties of the model-data combination. Model sensitivity to rescaling and transformations of the response [1] , the presence and effect of heterogeneity [2] , the need to employ ridge regression when collinearity is present [3] , all have the goal of improving the application and stability of the model-data combination and resulting fitted model. In the application of linear models, these issues extend to consideration of residual error behavior and diagnostic measures to detect the effects of outliers, collinearities and serial correlation. Discussion of these can be found in [4] .
The simple centering of data in linear models is often applied as a component of standardizing the variables in a regression, re-centering the means of the variables at zero. It can also be seen as a way to lower correlation among explanatory variables in some cases, but will have limited if any effect on ANOVA related test statistics and measures of goodness of fit in models when interaction terms are present in the model. This is due to the geometry of the test statistics involved which typically reflect standardized lengths of orthogonal projections which are invariant to centering. See for example [5] . In high dimensional linear models, centering allows for easier geometric interpretation of correlations among a set of centered vectors and is often an initial step in the analysis. Note that in data with nonlinear patterns, correlation based adjustments often does not make sense as they implicitly assume an underlying linear framework. A serious concern in this regard is model mis-specifica- tion, here the assumption of a linear model when underlying nonlinearity is present. Centering the data may induce bias and inaccurate estimation and testing.
Nonlinear regression models are also available to model data based patterns. The use of centering in such models can be challenging to interpret. Such models are common in many biological, ecological and economic applications and there is often less flexibility in the set of potential modifications available as theory often informs and restricts model choice. Examples can be found in [6] . In terms of inference, the Wald statistic tends to be more interpretable, even though the log-likelihood ratio and score function are more theoretically justified. The local curvature of the regression surface may require consideration if approximations based on local linear models are used to develop pivotal quantities for inference, especially in small samples with normal error.
In this paper, centering effects are examined in relation to the use of linear approximation in nonlinear regression models. To begin, the effects of centering in linear models with interaction effects are reviewed. Centering effects in nonlinear models where linear approximation is employed to obtain tests of significance are then discussed. Even in the presence of uncorrelated explanatory variables and simple main effects, centering may significantly affect locally defined linear approximations and related test statistics. Local measures of nonlinearity are defined and used to assess these effects. We then investigate the mis-specification of linear versus nonlinear models and show that centering effects arise as a measure of bias. This is particulary relevant in high dimensional data modeling where centeriing is common as a first step in data analysis.
2. Centering in Linear Models
We can write a standard linear model in the form

typically assuming the 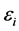 random errors are i.i.d.
random errors are i.i.d. . The
. The 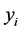 are the responses of interest, the
are the responses of interest, the 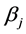 unknown parameters and the
unknown parameters and the 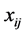 are explanatory variables taken here as known. The
are explanatory variables taken here as known. The 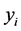 and
and 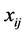 can be collected into vectors and matrices and re-expressed as
can be collected into vectors and matrices and re-expressed as  The model is quite flexible and can be transformed in many ways.
The model is quite flexible and can be transformed in many ways.
The use of centering in linear regression settings is typically suggested to lower correlation among the explanatory variables. For example, if 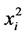 is entered in the model already containing
is entered in the model already containing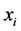 , centering will often lower the correlation between them. This will provide more stability in the interpretation of the fitted model. Centering is often thought to be useful when interaction terms are entered into the model, giving more stability in least squares based estimation. The cross-product term in regression models with interaction may be collinear with the main effects, making it difficult to detect identify both main and interaction effects. However in such models, as shown in [5] , mean-centering does not change the computational precision of parameters, the sampling accuracy of main effects, interaction effects, nor the
, centering will often lower the correlation between them. This will provide more stability in the interpretation of the fitted model. Centering is often thought to be useful when interaction terms are entered into the model, giving more stability in least squares based estimation. The cross-product term in regression models with interaction may be collinear with the main effects, making it difficult to detect identify both main and interaction effects. However in such models, as shown in [5] , mean-centering does not change the computational precision of parameters, the sampling accuracy of main effects, interaction effects, nor the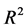 . The pivotal quantities and related test statis- tics for the main effects may require adjustment for this to be clear as the respective parameters may alter mean- ing.
. The pivotal quantities and related test statis- tics for the main effects may require adjustment for this to be clear as the respective parameters may alter mean- ing.
To see this, consider the simple linear regression model
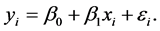
Centering by definition will not affect the shape of the initial 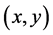 data cloud, it simply re-centers it to
data cloud, it simply re-centers it to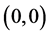 . The best fitting line will therefore not alter in terms of its slope and neither will the residuals of the fitted line. As the SSE is the squared length of the residuals, the MSE the average squared length and the goodness of fit measure R2
. The best fitting line will therefore not alter in terms of its slope and neither will the residuals of the fitted line. As the SSE is the squared length of the residuals, the MSE the average squared length and the goodness of fit measure R2 ![]() where
where ![]() these also do not alter with centering. The ols estimate for the slope,
these also do not alter with centering. The ols estimate for the slope, ![]() , is based on sums of differences from the x and y means and is invariant to centering, as is the correlation between x and y. The error distribution assumed does not affect these results. It is based on the initial assumption of normally distributed (theoretical) erros and the geometric properties of the least squares estimators. Note that the estimate for the intercept
, is based on sums of differences from the x and y means and is invariant to centering, as is the correlation between x and y. The error distribution assumed does not affect these results. It is based on the initial assumption of normally distributed (theoretical) erros and the geometric properties of the least squares estimators. Note that the estimate for the intercept ![]() will alter upon centering the data.
will alter upon centering the data.
For the multivariate linear model
![]()
the same basic argument related to residuals holds and the results are similar. The centering of all variables has no effect on the measures of association between the x and y variables, including the least squares estimators![]() . Note again that if terms of the form
. Note again that if terms of the form ![]() are added to the model, then centering may lower the correlation between the
are added to the model, then centering may lower the correlation between the ![]() and
and ![]() terms.
terms.
The addition of interaction terms ![]() to the linear model are a way of examining whether the relationship between y and
to the linear model are a way of examining whether the relationship between y and ![]() can be interpreted directly without accounting for the levels of another variable
can be interpreted directly without accounting for the levels of another variable![]() . If the coefficient for the respective interaction term is found to be significant, the main effect relating y and
. If the coefficient for the respective interaction term is found to be significant, the main effect relating y and ![]() cannot be directly assessed and stratification of the model may be necessary. Typically the multiple
cannot be directly assessed and stratification of the model may be necessary. Typically the multiple ![]() is taken to represent interaction effects as the partial derivative of the response with regard to either of the x will have the form
is taken to represent interaction effects as the partial derivative of the response with regard to either of the x will have the form
![]()
This implies that the main effect of ![]() is dependent on the level of
is dependent on the level of![]() . Note that the transformation
. Note that the transformation ![]() may remove a significant interaction.
may remove a significant interaction.
The centering of the data to limit potentially high levels of correlation between the interaction term![]() , and both
, and both ![]() and
and ![]() is sometimes suggested. As noted above this will not alter most measures of fit in the linear model (even a linear model where one of the variables is the interaction term). In particular, as shown in [5] , if we have as our model
is sometimes suggested. As noted above this will not alter most measures of fit in the linear model (even a linear model where one of the variables is the interaction term). In particular, as shown in [5] , if we have as our model
![]()
then the least squares estimate of the interaction term will not alter if ![]() and
and ![]() are centered, neither will the
are centered, neither will the ![]() value for the model. Note that the significance for the main effects in this model will appear to alter, but only due to the parameters having a different meaning in the centered model and thus related t-tests are testing slightly different hypotheses.
value for the model. Note that the significance for the main effects in this model will appear to alter, but only due to the parameters having a different meaning in the centered model and thus related t-tests are testing slightly different hypotheses.
3. Example 1
Consider the Penrose bodyfat ( [7] ) dataset of physiologic measurements where some measures are highly correlated. We look to predict bodyfat density as a function of several body measurements; Abdomen, Wrist, Weight, Hip, Knee, Ankle, Forearm, Biceps, Thigh, Chest. Three principal components account for 84% of the total variation in the data. Stepwise regression gives three variables (Abdomen, Weight, Wrist) accounting for an ![]() value of 73%. These variables have high correlations (0.88, 0.73, 0.62) which do not alter if we center the data. If we proceed to include interactions, dropping the Abdomen-Weight interaction due to extreme collinearity, we obtain a similar
value of 73%. These variables have high correlations (0.88, 0.73, 0.62) which do not alter if we center the data. If we proceed to include interactions, dropping the Abdomen-Weight interaction due to extreme collinearity, we obtain a similar ![]() value (73.1%). The correlations among the interactions themselves can be examined pre-centering (0.95, 0.96, 0.94) and post-centering (0.38, 0.90, 0.30) showing the effect of centering. We also obtain an overall F-test value of 133.95 (significant at 0.0001) which does not alter and
value (73.1%). The correlations among the interactions themselves can be examined pre-centering (0.95, 0.96, 0.94) and post-centering (0.38, 0.90, 0.30) showing the effect of centering. We also obtain an overall F-test value of 133.95 (significant at 0.0001) which does not alter and![]() , also invariant to centering. Further results are given in Table 1. Note that the OLS estimates for the interactions terms and their standard errors do not alter.
, also invariant to centering. Further results are given in Table 1. Note that the OLS estimates for the interactions terms and their standard errors do not alter.
4. Nonlinear Regression Models: Local Curvature Assessment
Nonlinear regression models typically are developed and applied in areas such as toxicology, economics and ecology. See [8] . Consider the nonlinear regression model
![]() (1)
(1)
(a) ![]() (b)
(b) ![]()
Table 1. Centering in linear models. (a) Original Data (S = 0.0099, R-sq = 73.1); (b) Centered Data (S = 0.0099 R-sq = 73.1).
![]() where
where ![]() are fixed values of the explanatory variable
are fixed values of the explanatory variable![]() , the model function
, the model function ![]() is known and depends on the parameter vector
is known and depends on the parameter vector ![]() and
and![]() . The
. The ![]() are independent error terms, each normally dis- tributed with mean zero and variance element
are independent error terms, each normally dis- tributed with mean zero and variance element![]() . The set of possible mean values defines a surface,
. The set of possible mean values defines a surface, ![]() , where
, where ![]() is the parameter space and
is the parameter space and ![]() is the
is the ![]() column vector with
column vector with ![]() com- ponent given by
com- ponent given by![]() . Some standard examples of nonlinear models include the Michaelis-Menten model
. Some standard examples of nonlinear models include the Michaelis-Menten model ![]() and the Logistic model;
and the Logistic model; ![]()
Nonlinear regression models are subject to the effects of centering when using local linear approximation. The relative position of the response y vis-a-vis the solution locus ![]() and the point on the surface at which the linear or tangent plane approximation is developed will affect the degree to which centering affects least squares based analysis of the model. In relation to the residual vector, an important aspect of the linear argument above, when there is intrinsic curvature present, the usual geometric properties of the residual vector are affected as they are the projection of an idempotent matrix only locally. Below we show that simply cen- tering the data affects the observed residuals, affects the level of a locally defined measure of intrinsic curvature and thus the linear approximation based analysis, and in the setting of misclassification, imputes bias into the analysis even to the first order.
and the point on the surface at which the linear or tangent plane approximation is developed will affect the degree to which centering affects least squares based analysis of the model. In relation to the residual vector, an important aspect of the linear argument above, when there is intrinsic curvature present, the usual geometric properties of the residual vector are affected as they are the projection of an idempotent matrix only locally. Below we show that simply cen- tering the data affects the observed residuals, affects the level of a locally defined measure of intrinsic curvature and thus the linear approximation based analysis, and in the setting of misclassification, imputes bias into the analysis even to the first order.
Local Geometry
Some geometry is briefly reviewed. Let ![]() be the
be the ![]() matrix with column elements given by
matrix with column elements given by
![]() for
for![]() . If
. If ![]() is the tangent plane to the surface N defined at
is the tangent plane to the surface N defined at![]() , then
, then
![]() is the orthogonal projection matrix for
is the orthogonal projection matrix for ![]() evaluated at
evaluated at![]() . Further
. Further
![]() is the projection of
is the projection of ![]() onto the tangent plane at
onto the tangent plane at![]() . Let
. Let
![]() , where
, where ![]() denotes length, be a unit vector centered at
denotes length, be a unit vector centered at ![]() on the tangent plane. The quadratic approximation to
on the tangent plane. The quadratic approximation to ![]() at
at ![]() is given by
is given by
![]() where
where ![]() is the Hessian
is the Hessian ![]() matrix with vector elements
matrix with vector elements
![]() evaluated at
evaluated at ![]() and
and![]() . The intrinsic acceleration vector in the direction u can
. The intrinsic acceleration vector in the direction u can
be expressed as ![]() or
or![]() , where
, where ![]() is the unit vector perpendicular to the acceleration vector in the direction
is the unit vector perpendicular to the acceleration vector in the direction ![]() and
and ![]() is the corresponding radius of curvature at
is the corresponding radius of curvature at![]() . We then have
. We then have
![]()
where![]() . Taking the norm gives the intrinsic local curvature
. Taking the norm gives the intrinsic local curvature
![]() (2)
(2)
where again![]() , all matrices are evaluated at
, all matrices are evaluated at![]() .
.
An intrinsic curvature based adjustment to standard ANOVA can be developed. See [9] . The usual orthogonal decomposition of regression and error can be replaced with the orthogonal decomposition ![]() with the residual space spanned by the intrinsic curvature vector
with the residual space spanned by the intrinsic curvature vector ![]() and the column vectors of
and the column vectors of![]() , which are orthonormal vectors spanning the remaining residual space dimensions, orthogonal to both tangent plane and
, which are orthonormal vectors spanning the remaining residual space dimensions, orthogonal to both tangent plane and![]() , evaluated at
, evaluated at![]() . The relevance of the curvature in the direction
. The relevance of the curvature in the direction ![]() at
at ![]() can be assessed by comparing the orthogonal projection(s) of
can be assessed by comparing the orthogonal projection(s) of ![]() onto
onto ![]() and
and ![]() respectively.
respectively.
To investigate this curvature effect in relation to the hypothesis ![]() an approximate linear model based approach can be used. A sum of squares regression component can generate a global F-test with p and
an approximate linear model based approach can be used. A sum of squares regression component can generate a global F-test with p and ![]() degrees of freedom. Assuming
degrees of freedom. Assuming ![]() where
where ![]() is unknown, we have under the null;
is unknown, we have under the null;
![]() (3)
(3)
with large values of the test statistic leading to rejection of ![]()
A further orthogonal decomposition gives a test of significance for curvature in the direction ![]() using orthogonal projection onto the vector
using orthogonal projection onto the vector![]() ;
;
![]() (4)
(4)
where ![]() A large value here reflects a significant projection length onto the curvature vector
A large value here reflects a significant projection length onto the curvature vector ![]() in the direction
in the direction![]() . The orthogonal projection onto the vector
. The orthogonal projection onto the vector ![]() also provides a correction factor for the global test
also provides a correction factor for the global test
![]()
See [10] for further details and application in regard to the testing of global null hypotheses. As the effect of intrinsic curvature depends where on the actual regression surface the linear approximation is developed in relation to the position of the response vector y, all of these test statistics may reflect centering effects.
5. Centering in Nonlinear Models
As in linear models, the use of centering on both response and some if not all of the explanatory variables initially would seem to have little or no effect on the underlying geometry of the model-data combination. A graph of the ![]() point cloud initially centered at
point cloud initially centered at ![]() will simply re-center at
will simply re-center at ![]() even if the overall pattern is nonlinear. However there may be effects on the subsequent analysis due to the nature of the nonlinear model and the locally linear frame of reference used for inference. The relative centering based shift in the
even if the overall pattern is nonlinear. However there may be effects on the subsequent analysis due to the nature of the nonlinear model and the locally linear frame of reference used for inference. The relative centering based shift in the ![]() surface versus the shift in the response y may alter the geometric relationship between y and
surface versus the shift in the response y may alter the geometric relationship between y and ![]() and the tangent plane relevant to the local approximation, related test statistics and orthogonal projections. These effects do not exist in the standard linear model setting as projections are taken onto the same flat surface with zero curvature at all points. Here the more curved the regression surface, the more the local frame of reference can be affected by small changes in the relative positioning of the response vector.
and the tangent plane relevant to the local approximation, related test statistics and orthogonal projections. These effects do not exist in the standard linear model setting as projections are taken onto the same flat surface with zero curvature at all points. Here the more curved the regression surface, the more the local frame of reference can be affected by small changes in the relative positioning of the response vector.
In regard to standard m.l.e. based analysis, the effects of centering will depend on the actual model itself. For example consider the asymptotic growth model
![]()
where centering the data yields
![]()
If the differences ![]() are relatively greater than
are relatively greater than ![]() then in terms of the response vector and regression surface the portion of the regression surface relevant to supporting the local linear approximation and analysis will alter. Note also that the parameters and their estimators in a nonlinear model are not easily interpreted as simple intercept and slope. They are often defined and justified in terms of underlying differential equations or asymptotic properties.
then in terms of the response vector and regression surface the portion of the regression surface relevant to supporting the local linear approximation and analysis will alter. Note also that the parameters and their estimators in a nonlinear model are not easily interpreted as simple intercept and slope. They are often defined and justified in terms of underlying differential equations or asymptotic properties.
The fundamental nature of a nonlinear regression model may be reflected in its possible forms under reparameterisation, especially in regard to re-expression as a linear model. If this is possible, then intrinsic cur- vature corrections tend to be of little value and centering can be seen to have the same non-effect as in standard linear models with regard to the rescaled parameters. For example, the Michaelis-Menten model is given by;
![]()
where ![]() are i.i.d.
are i.i.d.![]() . This can be re-expressed and re-parameterized as
. This can be re-expressed and re-parameterized as
![]()
![]()
Letting ![]() and
and ![]() the model has a linear form if this reformatting of the variables is acceptable. In some settings however this re-writing of the model may not be possible.
the model has a linear form if this reformatting of the variables is acceptable. In some settings however this re-writing of the model may not be possible.
For models which may not be re-expressed as linear models, we can assess the change in curvature effect at a given ![]() when centering the data
when centering the data ![]() using
using
![]()
The SSE values may also differ and together these alter the relevant F-statistics for the local ANOVA analysis discussed above. Note that while the raw data plot is simply re-centered, the local approximation and analysis reflecting the model-data combination is more strongly affected by centering.
6. Example 2
We examine these concepts further in the context of the asymptotic growth model applied to the BOD dataset found in Bates and Watts (1988). This is given by
![]()
The original and centered dataset is given in Table 2 and results from fitting the model based on the m.l.e. are given in Table 3.
The non-standard behavior of this model yields log-likelihood based confidence regions that are open at confidence levels above 95% in the ![]() direction and a linear approximation based analysis can be applied. The first order derivative matrix is n by 2 and can be written, for
direction and a linear approximation based analysis can be applied. The first order derivative matrix is n by 2 and can be written, for ![]()
![]()
with related 2 by 2 by n second order Hessian matrix
![]()
where each ![]() is an n-dimensional vector. The 0 value denotes a linear aspect to the model in certain direc- tions, sometimes called partially linear.
is an n-dimensional vector. The 0 value denotes a linear aspect to the model in certain direc- tions, sometimes called partially linear.
Note that the m.l.e. here is not available in closed form, rather it is defined by differentiating the log- likelihood with regard to each parameter and setting the resulting equations equal to zero. Here the log- likelihood is given by
![]()
Table 3. BOD Model Standard Output (![]() ).
).
![]()
Note that the effects of centering on the m.l.e. occur in this set of equations. Standard errors can be deter- mined from the inverse of the Fisher Information matrix.
For the original data, the resulting maximum likelihood or least squares value for ![]() is given by
is given by![]() ,
, ![]() with residual standard error
with residual standard error ![]() on 4 degrees of freedom. The residual vector is given by (0.41, −2.22, 3.75, −0.85, −2.20, 1.12). T-tests for for a difference from zero give p- values of 0.0015 and 0.059 respectively. For the centered data, the maximum likelihood values for
on 4 degrees of freedom. The residual vector is given by (0.41, −2.22, 3.75, −0.85, −2.20, 1.12). T-tests for for a difference from zero give p- values of 0.0015 and 0.059 respectively. For the centered data, the maximum likelihood values for ![]() are
are ![]() and
and ![]() with residual standard error
with residual standard error ![]() on 4 degrees of free- dom. The residual vector is given by (−0.29, 1.05, 5.41, 0.61, −1.24, 0.83). Comparing the maximum likelihood values is difficult as the meaning of the parameters alters. More importantly we can see that the residual vector and related SSE have altered due to centering.
on 4 degrees of free- dom. The residual vector is given by (−0.29, 1.05, 5.41, 0.61, −1.24, 0.83). Comparing the maximum likelihood values is difficult as the meaning of the parameters alters. More importantly we can see that the residual vector and related SSE have altered due to centering.
The curvature adjusted approach using ANOVA is given in Table 4 for a null value of![]() .
.
The measure
![]()
is examined here by comparing the SSCurv elements pre and post centering. This has a value pre-centering (0.40) that is approximately only 10% of its value post-centering (3.90). Whether this incurs statistically significant effects will depend on the local curvature of the surface, the manner in which the parameters enter into the model and the relative position of y in relation to ![]() and its linear approximation before and after centering. The results in Table 4 show the centering of the data affecting the formal significance of the global test.
and its linear approximation before and after centering. The results in Table 4 show the centering of the data affecting the formal significance of the global test.
7. Mis-Specification and Centering Related Bias
The use of linear models when the underlying model-data combination is nonlinear can lead to mis-specification error. It is interesting to consider this in relation to centering effect which can yield bias even where second order intrinsic curvature is not significant. In many high dimensional data analytic techniques the centering of the data is a standard first step. See for example [10] . However it is rare in those settings that linearlity can be confidently assumed.
To examine mis-specification generally in this setting, we begin by expressing a linear model as function of two sets of variables
![]()
Assume that the variables of interest form the ![]()
![]() matrix with
matrix with ![]() variables and the
variables and the ![]()
![]() matrix has
matrix has ![]() additional variables and
additional variables and![]() . The error distribution is given by
. The error distribution is given by![]() . The goal here is to identify significant variables in the
. The goal here is to identify significant variables in the ![]() matrix.
matrix.
Assume now that a true nonlinear model underlies the set of ![]() variables. Re-expressing our initial model we have
variables. Re-expressing our initial model we have
![]()
where ![]() is a nonlinear model for the
is a nonlinear model for the ![]() subset of variables. Replacing
subset of variables. Replacing ![]() with its Taylor expansion about
with its Taylor expansion about ![]() gives
gives
![]() (5)
(5)
where ![]() is a constant function of
is a constant function of ![]() and
and ![]() the relevant derivative. We can further write
the relevant derivative. We can further write
![]()
where ![]() and
and ![]()
If we fit the original linear model, mis-specification effects arise as we will use (i) ![]() instead of
instead of ![]() and (ii) apply a biased error distribution as the more appropriate error distribution with nonlinearity present is;
and (ii) apply a biased error distribution as the more appropriate error distribution with nonlinearity present is;![]() . This reflects a type of centering effect that will be incorporated into the approximate least squares based analysis to follow. Typically we evaluate this at
. This reflects a type of centering effect that will be incorporated into the approximate least squares based analysis to follow. Typically we evaluate this at ![]()
If the actual data are also centered, it follows that a data-based centering effect will further occur. Letting ![]() be the centering element we have as the resulting error distribution
be the centering element we have as the resulting error distribution
![]()
The effect of centering the data here may be to worsen the mis-specification related biasing effect. This will depend on how the linear and nonlinear elements in the W vector and ![]() matrix interact with the centered data
matrix interact with the centered data![]() . Note that if the Taylor expansion is to the second order, then intrinsic curvature also affects the usefulness of residuals. See [11] . Here we have shown that in a nonlinear model with the possibility of linear versus nonlinear mis-specification, bias results from simple first order issues and the centering of data.
. Note that if the Taylor expansion is to the second order, then intrinsic curvature also affects the usefulness of residuals. See [11] . Here we have shown that in a nonlinear model with the possibility of linear versus nonlinear mis-specification, bias results from simple first order issues and the centering of data.
8. Discussion
Model sensitivity and stability are essential components of applied research using probability modes. These are functions of the model structure, data structure and the inferential or estimation method used to fit the model. This is most pronounced when nonlinear models are to be employed and linear approximation is a component of the inferential process. Wald statistics are the most interpretable in this setting and in the case of nonlinear regression with normal error; the curvature of the regression surface is a key component affecting the accuracy of the inferential process. The underlying nature of the model is also relevant with linearity on same scale being reflected in the intrinsic curvature related calculations. These issues arise often in the analysis of high dimen- sional datasets where centering is a standard first step.
If we examine centering in the context of the original point cloud the effects of centering seem non-existent. But the information in the data is assessed in relation to the assumed linear or nonlinear model. The properties of the assumed model are thus relevant to the estimation and testing of parameters defined within the fitted local model. The positioning of the response vector y in n-space in relation to the p-dimensional nonlinear regression surface defines a local frame of reference for inference with the intrinsic curvature and even simple centering has effects in nonlinear models both generally and when linear approximation is employed. Nonlinear models often reflect theoretical results for carefully chosen parameter and data scaling. In conclusion, the centering of data in relation to nonlinear regression model should be applied and interpreted carefully.
Acknowledgements
We thank the Editor and the referee for their comments.