Received 27 November 2015; accepted 5 January 2016; published 8 January 2016

1. Introduction
The Higgs-like boson H(126) with mass 125.7 GeV discovered in 2012 [1] and promoted to “a Higgs” in 2013 has not been identified as the Standard Model (SM) Higgs boson, which is a point particle. In addition, the isospin = 1/2 of SM Higgs necessary to generate gauge boson masses has not been established for H(126); no charged Higgs has been found. H(126) is therefore not accounted for.
Since the H(126) mass is not too far from that of two charged gauge bosons W+ and W- or 2MW = 160.8 GeV, a bound state of W+W- will be considered. The spin and isospin of this state are both zero and no charged bound state is involved. Such composite type of approaches have been considered ( [2] , Status of Higgs Boson Physics) from models but not starting from any first principles’ theory. Here, such a bound state will be treated starting from the scalar strong interaction hadron theory (SSI) [3] at the quantum mechanics level.
In this theory, the gauge boson masses are naturally generated by pseudoscalar mesons ( [3] , §7.4.2) and Higgs is not needed. In Section 2, the equation of motion of the bound state is constructed from the equations of motion of gauge bosons in SSI. This equation is reduced in Section 3 to a nonlinear soliton-like radial differential equation which is solved in the linear limit. Estimate of the bound state mass is given. In Section 4, the fourth order nonlinear equation is transformed into a first order system together with boundary and continuity conditions and is solved on a computer. In Section 5, effects due to quantized fields are estimated by replacing the bare constants used above by renormalized ones. In view of these developments, the status of SM will be considered in Section 6.
2. Construction of Equation of Motion
Consider a gauge boson A located at space time xI , its action reads ( [3] , 7.1.2),
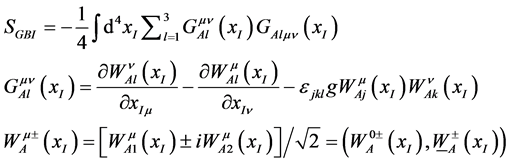 (1)
(1)
where  denotes the charged gauge bosons and the superscript 0 its time component.
denotes the charged gauge bosons and the superscript 0 its time component.
The gauge boson action (1) has been combined with meson and lepton actions ( [3] , 7.1.8, 7.11-12) to treat weak decays of kaons and pions. The sum of these three actions is varied with respect to 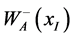 in ( [3] , §7.4.2) to yield the equation of motion for
in ( [3] , §7.4.2) to yield the equation of motion for 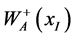 ( [3] , 7.4.7). The amplitude of this
( [3] , 7.4.7). The amplitude of this 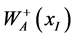 is controlled by the in-
is controlled by the in-
homogeneus lepton source term on the right side of this equation and is therefore small; the nonlinear gWW term in (1) becomes of higher order and can be neglected.
The lepton source term depends upon the time component  ([3] , 7.4.11c) which vanishes in the absence of lepton source current ( [3] , 7.4.8a). This is the present case. Also, weak decay is very slow so that long before the leptons materialize,
([3] , 7.4.11c) which vanishes in the absence of lepton source current ( [3] , 7.4.8a). This is the present case. Also, weak decay is very slow so that long before the leptons materialize,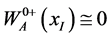 . Thus, only ( [3] , 7.4.8b) survives:
. Thus, only ( [3] , 7.4.8b) survives:
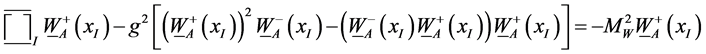 (2)
(2)
where the nonlinear gWW term in (1) neglected in ( [3] , 7.4.8b) but present in ( [3] , 7.4.7b) has been inserted in form of the g2WWW terms in (2) using ( [3] , 7.4.2c). This is necessary because without the inhomogeneus lepton
source term, the amplitude of 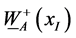 can be large so that g2 term in (2) cannot be neglected.
can be large so that g2 term in (2) cannot be neglected.
In (2), MW is the gauge boson mass ( [3] , 7.4.6b, 7.4.9) generated in SSI by virtual or real pions or kaons without any Higgs boson. In high energy p-p collisions, many W± bosons are produced close to each other. Consider another negatively charged boson B at nearby xII, . Its equation of motion can be obtained in an analogous way. The equivalent of (2) reads
. Its equation of motion can be obtained in an analogous way. The equivalent of (2) reads
 (3)
(3)
The nonlinear g2 terms couple W+ and W- and provide a weak confinement of them below.
To form a bound state, multiply together both sides of (2) and (3). This is entirely analogous to the formation of meson wave equations by multiplying together the left and right sides of the quark wave equations ( [3] , 2.1.1) and the antiquark wave equations ( [3] , 2.1.3). In both cases, the dynamic and interaction terms are on the left sides while the constant mass terms are on the right sides. Follow ( [3] , 2.2.1, 3.1.3a), generalize the product wave functions to a nonseparable bound state wave function
 (4)
(4)
where m = 1, 2, 3 denotes the spatial axes. The product equation reads
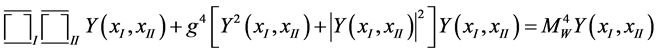 (5)
(5)
Here, generalizations of off diagonal tensor elements 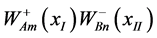 with m ¹ n have been dropped. This is analogous to leaving out the unseen diquarks of ( [3] , 2.2.2) in the product of the quark wave equations ( [3] , 2.1.1) and the antiquark wave equations ( [3] , 2.1.3) to arrive at the meson wave equations ( [3] , 2.2.4). Further,
with m ¹ n have been dropped. This is analogous to leaving out the unseen diquarks of ( [3] , 2.2.2) in the product of the quark wave equations ( [3] , 2.1.1) and the antiquark wave equations ( [3] , 2.1.3) to arrive at the meson wave equations ( [3] , 2.2.4). Further,
generalizations of doubly charged elements  are likewise left out. Also, the g2 terms have also been dropped because they contain
are likewise left out. Also, the g2 terms have also been dropped because they contain ![]() type of factors not paired off to
type of factors not paired off to ![]() type of expressions
type of expressions
and the final state contains no such unpaired gauge bosons. The corresponds to dropping the unpaired off quark wave functions to arrive at ( [3] , 2.2.4).
3. Reduction of Equation of Motion and Linear Solution
Following ( [3] , Sec 3.1), let
![]() (6)
(6)
Here, ![]() is the coordinate of the bound state Y.
is the coordinate of the bound state Y. ![]() is the relative coordinate between the both gauge bosons and is an observable contrary to x in ( [3] , 3.1.3a, 3.1.5a) which is a hidden variable because quarks are not observable.
is the relative coordinate between the both gauge bosons and is an observable contrary to x in ( [3] , 3.1.3a, 3.1.5a) which is a hidden variable because quarks are not observable.
For this bound state at rest, YB is independent of ![]() so that
so that![]() . Following ( [3] , 3.1.9), let
. Following ( [3] , 3.1.9), let![]() , where w0 is the relative energy between the both gauge bosons and is put to 0, analo-
, where w0 is the relative energy between the both gauge bosons and is put to 0, analo-
gous to the null relative energy condition ( [3] , §3.5.2). Thus, y(x) = y(x). Further, consider only the lowest energy state with zero angular momentum so that ![]() where r is the distance between the both
where r is the distance between the both
gauge bosons. It can now be shown that Y in (6) is real so that the both Y2 expressions inside the brackets of (5) are equal. Analogous to ( [3] , 3.1.10b), let ![]() where EB is the energy of the bound state. Now (5) can be reduced to
where EB is the energy of the bound state. Now (5) can be reduced to
![]() (7)
(7)
The nonlinear self interaction g4 term is of the same order as that in the action for Higgs boson and in some soliton equations. Although this coupling g is small, the resulting amplitude of y(r) may not be [4] . The second order derivatives in these point particle examples differs from the fourth order derivatives in (7), which describes a composite particle.
Putting g = 0, (7) is linearized and can be written in the form
![]() (8)
(8)
which reminds one of a particle moving in a three dimensional square well potential [5] and can be separated into
![]() (9)
(9)
Assume at first a- < 0. Since a+ > 0,
![]() (10)
(10)
where B and C are constants of dimension energy. The first of (10) satisfies the boundary condition y(r ® 0) = finite but not y(r ® ¥) = 0. The second of (10) satisfies the boundary condition y(r ® ¥) = 0 but not y(r ® 0) = finite. Analogous to the square well potential problem [5] , c+ and c− in (10) are joined at some radius r = ri by
requiring ![]() which leads to
which leads to
![]() (11)
(11)
that fixes ri. Inserting (10) into (8) gives EB = 2MW. With this value, the second of (8) does not lead to the assumed a- < 0 but to a- = 0. Although this a- does give![]() , this form of y(r) is not normalizable. Thus no bound state can be formed from (7) without the nonlinear g4 term; Coulomb attraction is negligible here.
, this form of y(r) is not normalizable. Thus no bound state can be formed from (7) without the nonlinear g4 term; Coulomb attraction is negligible here.
To obtain an estimate of EB, it is noted that the dimension of W± is energy. The only energy scale associated with free W± is its mass MW. By (4) and (6), y(r) in (7) may be put to ![]() in a dimensional approximation. Further, the D term in (7) will be neglected because the first of (10) holds for a small region r < ri and the second of (10) is not far from a constant because a- is not far from 0 according to the line following (11). For g2 = 0.4175 ( [3] , 7.2.1b, 7.2.12), close to g2 = (0.652)2 = 0.425 [6] , (7) leads to an estimate not far from 125.7 GeV;
in a dimensional approximation. Further, the D term in (7) will be neglected because the first of (10) holds for a small region r < ri and the second of (10) is not far from a constant because a- is not far from 0 according to the line following (11). For g2 = 0.4175 ( [3] , 7.2.1b, 7.2.12), close to g2 = (0.652)2 = 0.425 [6] , (7) leads to an estimate not far from 125.7 GeV;
![]() (12)
(12)
This relation leads via (8) to that the assumed a-<0 is satisfied.
4. Numerical Solution
Equation (7) has to be solved on a computer. Using the last of (9), (7) becomes
![]() (13)
(13)
which can be converted into a first order system like that done for baryons [3] ,
![]() (14)
(14)
When r ® 0, (14) and the first of (10) leads to
![]() (15)
(15)
As r ® ¥, the second of (10) satisfies (14) and the asymptotic solution is
![]() (16)
(16)
Numerical integration of (14) starts from r = 0 with (15) forward (w+) and from r @ ¥ with (16) backward (w-). Both solutions meet at ri and are joined there. Since (13) is of fourth order, there are three continuity requirements; corresponding to (11) are
![]() (17)
(17)
These three conditions fix the three unknown parameters, the bound state energy EB, the bound state amplitude B and the joint radius ri for a given g2. A Fortran 77 computer program has been written for (14)-(17) employing the Runge-Kutta integration subroutine “dverk” earlier used for the baryon wave functions ( [3] , Fig. 11.1). The calculations are run on computers of the Dept. of Information Technology at Uppsala University.
Dividing the left sides in (17) by their respective right sides gives 1 for each of the three conditions. The computed results will deviate from these three 1’s. Denote the greatest of these three deviations by Dmax. Let the amplitude![]() .
.
The forward integration mostly starts at r = 10-6 GeV−1 but other powers have also been used to check consistency. Because of (16), the backward integration must start from rather large r, here 0.5 GeV-1, but other values < 1 have also been employed to check consistency. This upper limit r < 1 is related to the minimum integration step length of 2-10 » 0.001 GeV-1 set by the “dverk” routine for this case. The parameter space![]() ,
, ![]() for g2 = 0.4175 and
for g2 = 0.4175 and ![]() has been scanned with rather fine meshes near the approximate solutions where Dmax reach minima. The results are
has been scanned with rather fine meshes near the approximate solutions where Dmax reach minima. The results are
![]() (18)
(18)
Here, the first two parameters can be chosen to any degree of accuracy. But ri can be specified only up to an accuracy of the above integration step length » 0.001 GeV-1 which is about Derr » 3% of ri in (18). This inaccuracy is expected to render the smallest Dmax values in (18) to be of the same magnitude, as is the case. For g2 = 0.4175, b0 = 1.945and the wave function c(r) is given by the full curve in Figure 1.
The existence of solution (18) shows that the gWW term in (1) which gives rise to the g4 term in (13) is responsible for a new nonlinear, intrinsic confinement mechanism at the quantum mechanical level. Because g4 is small, the confinement is weak, as is signified by that Eb»150.8 GeV in (18) is just slightly smaller than 2MW = 160.77 GeV. This confinement mechanism is implicit in the numerical treatment but not transparent and hence not understood presently.
The corresponding gWW term in the QCD Lagrangian density ( [4] , 18.3) also gives rise to confinement of colored quarks which is a quantum field theory effect [7] . These both confinement mechanisms are basically different. The present bound state is a counterpart to the QCD glueball.
5. Quantized Field Effects
The predicted EB of »155.81 GeV is too high to account for the H(126). However, Figure 1 shows that the distances between the both gauge bosons are very small, far smaller than those at which the bare g and MW are determined. At such distances, quantum field effects like vaccum polarization can no longer be neglected. Such effects are estimated below.
Return to the gauge boson action (1) and the meson action ( [3] , 7.1.8) mentioned beneath (1). These correspond to the QCD action formed from the QCD Lagrangian density ( [4] , 18.3). The SU(2) gluon part in this action is the same as (1) if the gluons are replaced by the gauge bosons W±. Therefore, quantization of this gluon part in ( [4] , Ch. 18) can be taken over to apply to (1). The remaining quark related part in the QCD action differ from the meson action ( [3] , 7.1.8); the former has been quantized in ( [4] , Ch. 18) while the latter is nonlocal and cannot be quantized ( [3] , Table 14.1). These parts provide the charges that generate the gluons and gauge bosons W±, respectively, but do not affect their actions.
The running coupling constant ( [4] , 18.155) adapted for SU(2) with no massless quarks reads
![]() (19)
(19)
![]()
Figure 1. Full curve: the bound state wave function c(r) for g2 = 0.4175 case in (18). Dotted curve: the bound state wave function c(r) for the Lf = 0.35 GeV-1 case in Table 1. The forward and backward integrations are joined at the dot marked points.
where L3 and l3 are two different normalization volumes corresponding to the both infrared cutoffs L and l in the logarithmically divergent integral ( [4] , 18.121) leading to (19). Let L = LR and g = gR, where R stands for “renormalized”. Choose l3 to be a large box ![]() in which the bare coupling constant g has been determined so that gl can be approximated by the bare g used above. In this case, (19) can be approximated to
in which the bare coupling constant g has been determined so that gl can be approximated by the bare g used above. In this case, (19) can be approximated to
![]() (20)
(20)
In the bound state, the both gauge bosons are so close to each other that the normalization volume for their wave functions are greatly reduced. The effect is roughly taken into account by the approximation LR ® r, the distance between the both gauge bosons, in (20).
The distances in Figure 1 are not extremely small and the Fermi constant ( [3] , 7.4.29a) µ ![]() may be assumed to remain valid there so that the renormalized gauge boson mass MWR becomes
may be assumed to remain valid there so that the renormalized gauge boson mass MWR becomes
![]() (21)
(21)
With MW = 80.385 GeV above, ( [3] , 7.4.29a) gives g2 = 0.426356. For this case, the calculations leading to (18) is repeated with the bare g and MW replaced by the renormalized gR(r) of (20) and MWR(r) of (21). Because r can be larger than Lf in the integration, the replacements are limited to Lf > r in (20). The results corresponding to (18) are shown in Table 1.
As for (18), solutions may exist only for the Dmax = 2.71 and 2.23 < Derr » 3% cases with Lf = 0.3, 0.35, The wave function c(r) for latter case is given by the dotted curve in Figure 1. Lf = 0.35 >> r for the dotted curve in Figure 1, as required and seems to be compatible with data.
For the second solution in Table 1, gR/g~0.957 at ri. By (21) MWR is also smaller than MW by ~4.3%. This reduction adds to that due to the g4 terms in (12-13) but both are too small to account for the lowering of Eb from 155.81 in (18) to 110 GeV in Table 1. This large difference has to be due to that the inclusion of the running gR(r) and MWR(r) switches the radially excited mode (full curve) to the ground state mode (dotted curve) in Figure 1. Again, this switching mechanism is hidden behind the numerical integrations and is also not understood.
Eb = 110 GeV is, however, too low and may be due to the coarse approximations made to obtain Table 1. One of them is the application of the (19) in which the logarithmic term comes from ( [4] , 18.121)
![]() (22)
(22)
Here, ![]() , k the gauge boson momentum, q the angle between this momentum and the third axis, L the ultraviolet cutoff. The right member of (22) is obtained assuming spherical symmetry in the integral. In the bound state case, there is a new axis of symmetry connecting the both gauge bosons and the appropriate symmetry is cylindrical. In this case, the integration in (22) cannot be carried out explicitly and numerical treatment becomes very cumbersome.
, k the gauge boson momentum, q the angle between this momentum and the third axis, L the ultraviolet cutoff. The right member of (22) is obtained assuming spherical symmetry in the integral. In the bound state case, there is a new axis of symmetry connecting the both gauge bosons and the appropriate symmetry is cylindrical. In this case, the integration in (22) cannot be carried out explicitly and numerical treatment becomes very cumbersome.
LHC results on composite Higgs boson are expected in 2016 [8] . These, if conclusive, will be of crucial importance for SM, as will be considered below
6. On the Status of the Standard Model
In the electroweak sector, Higgs field is based upon the idea of spontaneous symmetry breaking which comes from solid state physics and superconductivity which has superconducting material with Cooper pairs as background.
![]()
Table 1. Results of numerical solution of (14)-(17) with the bare g and MW replaced by the renormalized gR(r) of (20) and MWR(r) of (21) for the g2 = 0.426356. EB, b0, and ri for each Lf are varied such that Dmax, the greatest deviation from the exact (17), reaches a minimum. Only the two underlined cases with Dmax < Derr » 3% have confined solutions.
The SM-QCD vacuum has no known material background. The mechanisms in superconductivity can therefore not be taken over to apply to SM-QCD vacuum without further justification. Spontaneous symmetry breaking in the Higgs field in SM has been put in “by hand” and is therefore ad hoc.
From a historical point of view, new physics come out of mathematics starting from some principle and is not found by putting known physical mechanism into the formalism ( [3] , Appendix G, Sec. 6, §5.5), as is done in the introduction of the Higgs boson. That no SM Higgs has been established is therefore not surprising theoretically.
Without Higgs, SM cannot generate gauge boson mass and the main, electroweak sector of SM becomes without foundation. Here, SSI ( [3] , Ch. 7) steps in and fills part of the void left behind.
The strong interaction sector is basically unaffected by the above development but remains unproductive in low energy predictions. In any known basic discipline, the starting point is a set of differential equations (Newton, Maxwell, Dirac,…) which contains all physics. Lagrangians are subsequently constructed from these differential equations. Here, QCD starts from a Lagrangian containing unobservable wave function amplitudes of colored quarks and gluons. When converted to differential equations, these amplitudes cannot make contact with data. SSI [3] follows the historical path and starts with sets of equations of motion for mesons and baryons whose amplitudes are observables. It can in this way account for many basics low energy hadronic data (confinement, spectra,…) that QCD has failed to do so despite decades of effort.
At high energies, the confinement potential in SSI becomes small in comparison and the quarks behave more like free particles and QCD applies ([3] , Ch. 14).