Viscous and Joules Dissipation on MHD Flow past a Stretching Porous Surface Embedded in a Porous Medium ()
Received 29 October 2015; accepted 27 December 2015; published 30 December 2015

1. Introduction
Viscous dissipation changes the temperature distributions by playing a role like an energy source, which leads to affected heat transfer rates. The merit of the effect of viscous dissipation depends on whether the plate is being cooled or heated. Apart from the viscous dissipation in MHD flows, the Joules dissipation also acts as a volumetric heat source. Heat transfer analysis over porous surface is of much practical interest due to its abundant applications, such as, heat-treated materials traveling between a feed roll and wind-up roll, materials manufactured by extrusion, glass-fiber and paper production, cooling of metallic sheets, electronic chips and crystal growing. In view of all these aspects, Anjali Devi [1] deals with the effect of viscous and Joules dissipation on MHD flow, heat and mass transfer over a porous surface embedded in a porous medium. An analysis of thermal boundary layer in an electrically conducting fluid over a linearly stretching sheet in the presence of a constant transverse magnetic field with suction or blowing at the sheet was carried out by Chaim [2] . The viscous and joules dissipation and internal heat generation were taken into account in the energy equation. Very recently, the viscous and joules dissipation and internal heat generation were taken into account in the energy equation. Sajid et al. [3] investigated the non-similar analytic solution for MHD flow and heat transfer in a third-order fluid over a stretching sheet. He found that the skin friction coefficient decreased as the magnetic parameter or the third grade parameter increased. A mathematical analysis has been carried out on momentum and heat transfer characteristics in an incompressible, electrically conducting viscoelastic boundary layer fluid flow over a linear stretching sheet by Abel et al. [4] . A numerical reinvestigation of MHD boundary layer flow over a heated stretching sheet with variable viscosity has been analyzed by Pantokratoras [5] . Hence the present study investigates the effect viscous and Joules dissipation on MHD flow, heat and mass transfer over a porous surface embedded in a porous medium for rotating case.
2. Mathematical Analysis
Two-dimensional, nonlinear, steady, MHD laminar boundary layer flow with heat and mass transfer of a viscous, incompressible and electrically conducting fluid over a porous surface embedded in a porous medium in the presence of a transverse magnetic field including viscous and Joules dissipation is considered for investigation. An uniform transverse magnetic field of strength 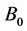 is applied parallel to y-axis. Consider a polymer sheet emerging out of a slit at
is applied parallel to y-axis. Consider a polymer sheet emerging out of a slit at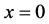 ,
, 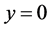 and subsequently being stretched, as in a polymer extrusion process. Let us assume that the speed at a point in the plate is proportional to the power of its distance from the slit and the boundary layer approximations are applicable. In writing the following equations, it is assumed that the induced magnetic field, the external electric field and the electric field due to the polarization of charges are negligible. Under these conditions, the governing boundary layer equations of momentum, energy and diffusion with viscous and Joules dissipation are
and subsequently being stretched, as in a polymer extrusion process. Let us assume that the speed at a point in the plate is proportional to the power of its distance from the slit and the boundary layer approximations are applicable. In writing the following equations, it is assumed that the induced magnetic field, the external electric field and the electric field due to the polarization of charges are negligible. Under these conditions, the governing boundary layer equations of momentum, energy and diffusion with viscous and Joules dissipation are
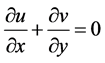 (1)
(1)
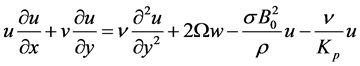 (2)
(2)
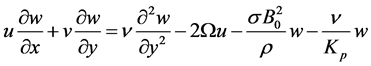 (3)
(3)
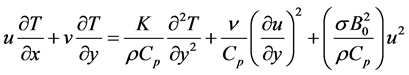 (4)
(4)
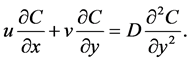 (5)
(5)
The boundary conditions are
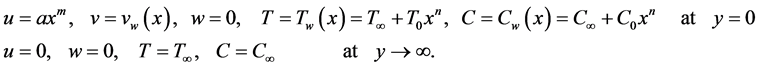 (6)
(6)
Here u, v are components of velocity components in the 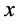 and
and 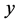 directions,
directions, 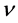 is kinematic coefficient of viscosity,
is kinematic coefficient of viscosity, 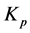 is permeability of the medium,
is permeability of the medium, 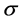 is electrical conductivity of the fluid,
is electrical conductivity of the fluid, 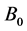 is applied magnetic field,
is applied magnetic field, ![]() is density of the fluid,
is density of the fluid, ![]() is temperature of the fluid,
is temperature of the fluid, ![]() is wall temperature,
is wall temperature, ![]() is temperature far away from the surface,
is temperature far away from the surface, ![]() is thermal conductivity,
is thermal conductivity, ![]() is specific heat at constant pressure,
is specific heat at constant pressure, ![]() is species concentration of the fluid,
is species concentration of the fluid, ![]() is species concentration near the wall
is species concentration near the wall ![]() is species concentration of the fluid away from the wall,
is species concentration of the fluid away from the wall, ![]() is diffusivity coefficient, a,
is diffusivity coefficient, a, ![]() and
and ![]() are dimensional constants,
are dimensional constants, ![]() is index of power-law velocity and
is index of power-law velocity and ![]() is index of power-law variation of wall temperature which is constant.
is index of power-law variation of wall temperature which is constant.
We introduce the following similarity transformations are
![]() (7)
(7)
where ![]() for suction at the stretching plate and
for suction at the stretching plate and ![]() is the stream function.
is the stream function.
The velocity components are given by
![]() (8)
(8)
It can be easily verified that the continuity Equation (1) is identically satisfied and introduce the non-dimen- sional form of temperature and concentration as
![]() (9)
(9)
Hence Equations (2)-(5) and boundary conditions (6) reduced to:
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
The corresponding boundary conditions are
![]() (14)
(14)
where, ![]() (Stretching parameter),
(Stretching parameter), ![]() (Magnetic parameter),
(Magnetic parameter), ![]() (Permeability parameter),
(Permeability parameter), ![]() (Prandtl number),
(Prandtl number), ![]() (Eckert number),
(Eckert number), ![]() (Schmidt num- ber),
(Schmidt num- ber), ![]() (Rotation parameter).
(Rotation parameter).
3. Results and Discussions
In Figure 1, transverse velocity profiles decreases with the increase of![]() . In Figure 2, primary velocity profiles increases with the increase of
. In Figure 2, primary velocity profiles increases with the increase of![]() . In Figure 3, primary shear stress profiles increases with the increase of
. In Figure 3, primary shear stress profiles increases with the increase of![]() . In Figure 4, secondary velocity profiles increases with the increase of
. In Figure 4, secondary velocity profiles increases with the increase of![]() . In Figure 5, secondary shear stress profiles increases with the increase of
. In Figure 5, secondary shear stress profiles increases with the increase of![]() . In Figure 6, temperature profiles decreases with the increase of
. In Figure 6, temperature profiles decreases with the increase of![]() . In Figure 7, Nusselt number profiles increases with the increase of
. In Figure 7, Nusselt number profiles increases with the increase of![]() . In Figure 8, concentration profiles decreases with the increase of
. In Figure 8, concentration profiles decreases with the increase of![]() . In Figure 9, Sherwood number profiles increases with the increase of
. In Figure 9, Sherwood number profiles increases with the increase of![]() . In Figure 10, transverse velocity profiles increases with the increase of
. In Figure 10, transverse velocity profiles increases with the increase of![]() .
.
In Figure 11, primary velocity profiles increases with the increase of![]() . In Figure 12, primary shear stress profiles increases with the increase of
. In Figure 12, primary shear stress profiles increases with the increase of![]() . In Figure 13, secondary velocity profiles increases (slightly) with the increase of
. In Figure 13, secondary velocity profiles increases (slightly) with the increase of![]() . In Figure 14, secondary Shear Stress profiles increases with the increase of
. In Figure 14, secondary Shear Stress profiles increases with the increase of![]() . In Figure 15, temperature profiles increases with the increase of
. In Figure 15, temperature profiles increases with the increase of![]() . In Figure 16, Nusselt number profiles decreases with the increase of
. In Figure 16, Nusselt number profiles decreases with the increase of ![]() In Figure 17, concentration profiles remains same for the variation of
In Figure 17, concentration profiles remains same for the variation of![]() . In Figure 18, Sherwood number profiles remains same for the variation of
. In Figure 18, Sherwood number profiles remains same for the variation of![]() . In Figure 19, transverse velocity profiles increases with the increase of
. In Figure 19, transverse velocity profiles increases with the increase of![]() . In Figure 20, primary velocity profiles decreases with the increase of
. In Figure 20, primary velocity profiles decreases with the increase of![]() . In Figure 21, primary shear stress profiles decreases with the increase of
. In Figure 21, primary shear stress profiles decreases with the increase of![]() . In Figure 22, secondary velocity profiles first increases then decreases with the increase of
. In Figure 22, secondary velocity profiles first increases then decreases with the increase of![]() . In Figure 23, secondary shear stress profiles decreases with the increase of
. In Figure 23, secondary shear stress profiles decreases with the increase of![]() . In Figure 24, temperature profiles decreases with the increase of
. In Figure 24, temperature profiles decreases with the increase of![]() . In Figure 25, Nusselt number profiles increases with the increase of
. In Figure 25, Nusselt number profiles increases with the increase of![]() . In Figure 26, concentration profiles decreases with the increase of
. In Figure 26, concentration profiles decreases with the increase of![]() . In Figure 27, Sherwood number profiles increases with the increase of
. In Figure 27, Sherwood number profiles increases with the increase of![]() . In Figure 28, transverse velocity profiles decreases with the increase of
. In Figure 28, transverse velocity profiles decreases with the increase of![]() . In Figure 29, primary velocity profiles decreases with the increase of
. In Figure 29, primary velocity profiles decreases with the increase of![]() . In Figure 30, primary shear stress profiles decreases then increases with the increase of
. In Figure 30, primary shear stress profiles decreases then increases with the increase of![]() . In Figure 31, secondary velocity profiles first increases then decreases with the increase of
. In Figure 31, secondary velocity profiles first increases then decreases with the increase of![]() . In Figure 32, secondary shear stress profiles decreases with the increase of
. In Figure 32, secondary shear stress profiles decreases with the increase of![]() . In Figure 33, temperature profiles increases with the increase of
. In Figure 33, temperature profiles increases with the increase of![]() . In Figure 34, Nusselt number profiles decreases with the increase of
. In Figure 34, Nusselt number profiles decreases with the increase of![]() . In Figure 35, concentration profiles decreases with the increase of
. In Figure 35, concentration profiles decreases with the increase of![]() . In Figure 36, Sherwood number profiles increases with the increase of
. In Figure 36, Sherwood number profiles increases with the increase of![]() .
.
![]()
Figure 1. Transverse velocity profiles for β.
![]()
Figure 2. Primary velocity profiles for β.
![]()
Figure 3. Primary shear stress profile for β.
![]()
Figure 4. Secondary velocity profile for β.
![]()
Figure 5. Secondary shear stress profile for β.
![]()
Figure 9. Sherwood number profiles for β.
![]()
Figure 10. Transverse velocity profiles for Ec.
![]()
Figure 12. Primary shear stress profile for Ec.
![]()
Figure 13. Secondary velocity profile for Ec.
![]()
Figure 14. Secondary shear stress profile for Ec.
![]()
Figure 19. Transverse velocity profiles for λ.
![]()
Figure 21. Primary shear stress profiles for λ.
![]()
Figure 22. Secondary velocity profiles for λ.
![]()
Figure 23. Secondary shear stress profiles for λ.
![]()
Figure 28. Transverse velocity profiles for λ.
![]()
Figure 30. Primary shear stress profiles for M2.
![]()
Figure 31. Secondary velocity profiles for M2.
![]()
Figure 32. Secondary shear stress profiles for M2.
4. Conclusion
The effect of viscous and joules dissipation on MHD flow with heat and mass transfer past a stretching porous surface embedded in a porous medium is analyzed in the present study for rotating case. Increasing, decreasing and cross flows occur for the variation of different parameters.