New Method of Determining the Landau Levels in Narrow-Gap Semiconductors ()
Received 28 October 2015; accepted 12 December 2015; published 15 December 2015


1. Introduction
In narrow-gap semiconductors, the effective mass of electrons is small, so that the quantization condition is observed in weak magnetic fields. In such conditions, the distance between Landau levels was greater than the
characteristic electron energy. In these conditions, it is possible to find the effective mass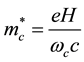 . This effect-
. This effect-
tive mass is associated with transitions between Landau energy levels. However, if the dependence of the energy of the wave vector is not described by a quadratic form, for example, the electron in InSb energy levels of the
charge carriers in the magnetic field is not at equidistants, such as the cyclotron mass, but is given by 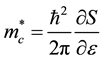 [1] , and hence the cyclotron frequency depends on E and kz.
[1] , and hence the cyclotron frequency depends on E and kz.
The works [2] - [4] studied the temperature dependence of the energy spectrum of the density of states of semiconductors in view of the temperature dependence of the effective mass of the density of states. In this work, it did not consider the effect of the cyclotron effective mass on the temperature dependence of the density of the energy states in a strong magnetic field. However, experiments as shown in [5] - [7] , the effective mass depends on energy. These changes in the cyclotron effective mass alter energy density of states in a strong quantizing magnetic field.
The temperature dependence of the density of states is due to thermal broadening of discrete energy states [3] . Thermal broadening can be described by the temperature dependence of the occupation probabilities of the energy levels. Time thermal emission of electrons from deep levels Ei in the allowed band energy E is determined by the
exponential factor 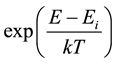 and the probability of deep desolation filled levels depends exponentially on the energy of the state and the sample temperature.
and the probability of deep desolation filled levels depends exponentially on the energy of the state and the sample temperature.
The aim of this work is to study the influence changes in the cyclotron effective mass at the temperature dependence of the density of the energy states in a strong quantizing magnetic field.
2. Method
In a strong magnetic field, the energy spectrum of free electrons and holes are undergoing serious changes, which is reflected by the density of the energy states. The dependence of the energy E of the electron with a quadratic ellipsoidal dispersion law in the magnetic field on the principal quantum number n, the number of quanta of the spin s, and the projection pz momentum on the direction of the magnetic field H take the next view [8] :
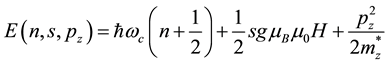 . (1)
. (1)
Here, g-factor is determined only by the orientation of the magnetic field H and does not depend on the quantity projection of the momentum pz―pulse,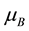 ―Bohr magneton and mz―longitudinal effective mass.
―Bohr magneton and mz―longitudinal effective mass.
The total density of energy states in a magnetic field, and the electronic system with a quadratic isotropic dispersion law excluding spinal splitting of the Landau levels can be written as [8] :
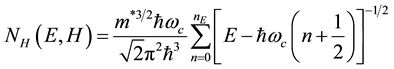 (2)
(2)
where E is the energy of a free electron, 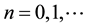 is the number of the Landau levels, m* is the effective mass of the cyclotron,
is the number of the Landau levels, m* is the effective mass of the cyclotron, 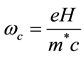 is the cyclotron frequency.
is the cyclotron frequency.
At particular, if the energy spectrum is purely discrete, then the density of energy states is equal to the sum of δ-functions concentrated at the points of the spectrum Ei, where amplitude is 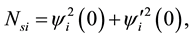 and
and 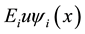 is normalized to unity own functions [9] :
is normalized to unity own functions [9] :
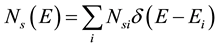 . (3)
. (3)
Thermal broadening of the levels in the magnetic field leads to a smoothing of discrete levels. Thermal broadening is considered by GN function. As in [10] [11] , 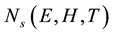 in a series in functions of GN
in a series in functions of GN
 (4)
(4)
where 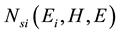 is the density of states in a quantizing magnetic field at a temperature of absolute zero.
is the density of states in a quantizing magnetic field at a temperature of absolute zero.
If the dispersion law is non-quadratic, but isotropic, for example, the electrons in III-V compounds and II-VI, the effective mass is a function of the wave number and energy. This means that the filling of the energy band effective mass of carriers will change [1] .
The works [12] [13] determined the effective mass of carriers at the Fermi level in semiconductors InSb c using a Fourier spectrometer. Figure 1 shows the dependence of the effective mass of the energy in InSb from the works
![]()
Figure 1. The dependence of the effective mass of energy in InSb [12] [13] .
[12] [13] . Figure 1 is also shown the calculated dependence to the effective mass from quantity magnetic field. The effective mass depends on the energy in a strong magnetic field:
![]() (5)
(5)
where, Eg is bandgap, m is effective mass of the electrons at the bottom of the conduction band, Ee is energy of the electrons:![]() .
.
The use of several fitting parameters leads to ambiguity determining the value of ![]() which is equal to 1.16.
which is equal to 1.16.
In the works [2] [3] , it was shown that the continuous spectrum of the thermodynamic density of states at low temperatures will turn to the discrete spectrum of the density of states. With the expansion of the energy spectrum of the density of states, function GN derivative in energy from the energy level of occupation probabilities was shown that the magnitude of the energy gaps would depend on the temperature. The temperature dependence of the band gap is determined by the temperature dependence of the density of the energy state of the conduction band and valence band of the semiconductor. Thermal broadening of the density of states is due to near the bottom of the conduction band and valence band is reduced bandgap.
Then the cyclotron effective mass can be represented as follows:
![]() . (6)
. (6)
From here you can write the density of energy states as follows:
![]() . (7)
. (7)
The effect of the change on the mass density of states in a magnetic field is considered. This can be considered as a deviation of the electron dispersion from parabolic.
3. Influence of the Effective Mass on the Temperature Dependence of the Density of Energy States
In a strong magnetic field, continuous spectrum of energy states is strongly deformed and transformed into oscillating line. With increasing temperature, the discrete levels are washed away, and the density of the energy states is converted into a continuous spectrum. In the experiment, the density of states depends on the energy, and the temperature of the effective mass. The effective mass depends on energy; and cyclotron resonance depends on the effective mass. Thus, with increasing energy changes, the distance is between the peaks.
Changing ![]() alters the energy separation between the peaks of the Landau levels. Thus, the oscillations of the density of states is observed at temperatures
alters the energy separation between the peaks of the Landau levels. Thus, the oscillations of the density of states is observed at temperatures![]() . Beginning with temperatures of
. Beginning with temperatures of![]() , the
, the
oscillations of the density of states are due to the Landau quantization that is observed. In this case, the measurements provide a continuous range of density of states. The detection of quantum levels is necessary to solve the inverse problem. In this case, it is necessary to find a discrete level due to the Landau quantization. For this, it is necessary to measure![]() , and the temperature of the experiment, followed by calculation to obtain
, and the temperature of the experiment, followed by calculation to obtain ![]() at low temperatures.
at low temperatures.
At a constant effective mass (parabolic zone), the dependence of the energy density of states is given![]() . If the growth of electron energy increases, the effective electron mass decreases the distance
. If the growth of electron energy increases, the effective electron mass decreases the distance
between Landau levels, the curve of the density of states moved to larger values will shift the density of states, and travel up along the axis of the density of states. Conversely, if ![]() decreases with the increasing energy, the density of states moves down to the energy along the axis of the density of states. Thus, the magnetic field shifts the density of states in the plane,
decreases with the increasing energy, the density of states moves down to the energy along the axis of the density of states. Thus, the magnetic field shifts the density of states in the plane, ![]() , even at temperatures as Landau levels are not noticeable.
, even at temperatures as Landau levels are not noticeable.
Using the data of Figure 1, you can calculate the change in the effective mass on the temperature dependence of the density of the energy states in a strong magnetic field. Figure 2 shows a graph of the temperature dependence of the density of energy states for InSb, taking into account changes in the effective mass. Figure 2 shows that the change in the effective mass of energy can greatly affect the temperature dependence of the density of the energy states in a quantizing magnetic field.
4. Conclusion
We developed a method for determining the density of energy states in a quantizing magnetic field. With the help of mathematical models, the temperature dependence of the density of energy states in strong magnetic fields on semiconductors is determined. It is shown for the non-parabolic dispersion law that the density of states in a high magnetic field at an increased temperature coincides with the density of states in the sample without magnetic field. On the basis of this model, we used data on the high-temperature Ns to calculate the low-temperature density of states.
Acknowledgements
This work was supported by government grants of Uzbekistan F2-21 “Mathematical modeling of the determination of the density of surface states at the semiconductor-insulator”.