Lax-Friedrich Scheme for the Numerical Simulation of a Traffic Flow Model Based on a Nonlinear Velocity Density Relation ()
1. Introduction
With the increasingly rapid economic globalization and urbanization, more problems are brought to our attention. One of them is traffic jams. Traffic jams are now a major problem in most of the cities. So at the core of traffic congestion, development of traffic management is the need of time. Therefore, an efficient traffic control and management is essential in order to get rid of such huge traffic congestion. Modeling and computer simulation play an increasing role in the flow management. Many scientists have been working to develop various mathematical models [1] [2] in order to describe traffic flow. In this paper, we consider a macroscopic traffic model developed first by Lighthill and Whitham (1955) [3] [4] and Richard (1956) shortly called LWR model based on Habermann (1977) [5] , Klar (1996) [6] . In [7] , L. S. Andallah, Shajib Ali, M. O. Gani, M. K. Pandit and J. Akhter have used Linear Velocity-Density Function and in [8] , M. H. Kabir, M. O. Gani and L. S. Andallah have used Non-Linear Velocity-Density Function for the development of Traffic Flow Model. In [8] , they have presented explicit upwind difference scheme. We have also used a non-linear velocity-density relationship but we have presented the Lax-Friedrich’s scheme for the development of our model. We have established a well-po- sedness and stability condition of the Lax-Friedrich’s scheme. The numerical scheme is implemented in order to perform the numerical features of error estimation and rate of convergence. Finally, fundamental diagram, density, velocity and flux profiles are presented.
2. General Feature of the Model
In this section, the general features of the model are shortly presented based on [6] [7] [9] and work out the qualitative behavior of the flux. The well-known LWR model is formulated by employing the conservation equation
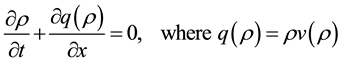 (1)
(1)
A non-linear velocity-density relationship [7] (non-linear function) can be of the form
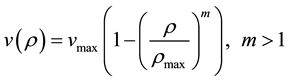 (2)
(2)
In this paper, we will use the non-linear velocity-density relationship (for m = 2 in (2)' as
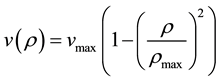 (3)
(3)
Now, substituting (3) in 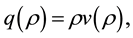 it produces a relationship for the traffic flux or flow as a function of density:
it produces a relationship for the traffic flux or flow as a function of density:
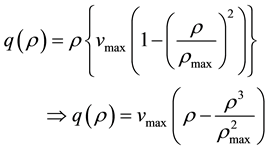 (4)
(4)
Now, we put flow-density function (4) into the general non-linear model partial differential equation (PDE) (1), we obtain the specific non-linear partial differential equation in the form
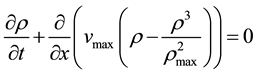 (5)
(5)
2.1. Qualitative Behavior of Non-Linear Traffic Velocity ν(ρ) (Figure 1)
There is a connection between traffic density and vehicle velocity. If there is more vehicles are on a road then their velocity will be slower. On the basis of observations of traffic flow, we make a basic simplifying assumption that the velocity of a car at any point along the highway depends only on the traffic density. Drivers speed up when traffic is sparse and they slow down when traffic is dense. Thus, there is a direct relationship between traffic density and traffic velocity as  . Now in order to deal with the non-linear model (1) it is necessary to understand the relation
. Now in order to deal with the non-linear model (1) it is necessary to understand the relation 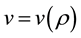 a bit more.
a bit more.
Based on the intuition mentioned above, one may assume that a driver will drive fastest, with velocity, say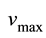 , when the density is at its smallest value,
, when the density is at its smallest value, . The velocity decreases as the density increases, which is a statement about the slope of the velocity, ν versus density, ρ curve. Assume further that the traffic is
. The velocity decreases as the density increases, which is a statement about the slope of the velocity, ν versus density, ρ curve. Assume further that the traffic is
bumper-to-bumper, i.e. ν = 0 , at some maximum density 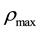 with
with 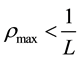 , where L is the average length
, where L is the average length
of a vehicle. We summarize these experience-born intuitions in mathematical requirements on the function, 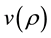 .
.
 (6)
(6)
2.2. Qualitative Behavior of Non-Linear Traffic Flow (Flux) q(ρ) (Figure 2)
The flow or flux given by Equation (4) is a cubic non-linear function. The maximum flow (flux) occurs when its
slope vanishes and 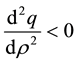 i.e.
i.e. 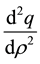 is negative. Now,
is negative. Now,
![]()
![]()
Therefore, ![]()
So, ![]() is negative. Therefore,
is negative. Therefore, ![]() is concave down and the flow (flux) is maximum at
is concave down and the flow (flux) is maximum at ![]() and
and
the maximum flow (flux) is
![]() (7)
(7)
3. Exact Solution of the Non-Linear PDE
The traffic flow model appended with the initial condition reads as initial value problem (IVP) is
![]()
Figure 1. Qualitative behavior of traffic velocity.
![]()
Figure 2. Qualitative behavior of traffic flow.
![]() (8)
(8)
The exact solution [8] of the IVP (8) is given by
![]() (9)
(9)
which is non-linear implicit form and therefore very complicated to evaluate at each ![]()
Moreover, in reality it is very complicated to approximate the initial density ![]() of the Cauchy problem (8) as a function of x from given initial data. Therefore, there is a demand of efficient numerical methods for solving the IVP (8).
of the Cauchy problem (8) as a function of x from given initial data. Therefore, there is a demand of efficient numerical methods for solving the IVP (8).
4. A Finite Difference Scheme for the Model of IBVP
For the numerical solution of the traffic flow model, we consider our specific non-linear traffic model problem as an initial and two points boundary value problem
![]() (10)
(10)
![]()
For the model, the numerical solution based on [9] [10] is
![]() (11)
(11)
where,
![]() (12)
(12)
This difference equation is known as Lax-Friedrich’s scheme.
However for the flux function (12), the scheme is not straight forward to implement. One needs to work stability condition and sub-sequel physical constraint condition for the scheme. Now we will study the well-po- sedness and stability condition of this scheme for our model.
5. Stability Condition and Physical Constraint Conditions
Rewrite the non-linear PDE in (8) as
![]()
Then the scheme (11) can be written as
![]() (13)
(13)
![]()
![]()
For well-posedness,![]() . It is evident that
. It is evident that
![]()
Here, ![]() is essentially positive.
is essentially positive.
Therefore, we have
![]() (14)
(14)
This is the condition of well-posedness.
![]() (15)
(15)
Now from Equation (13), we have
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
The Equation (18) implies that if ![]() , the new solution in a grid point is a convex combination of the two solutions of two difference grid point of the previous time.
, the new solution in a grid point is a convex combination of the two solutions of two difference grid point of the previous time.
![]() (19)
(19)
Then condition (17) can be guaranteed via (13) by
![]() (20)
(20)
which is the stability condition involving the parameter ![]() .
.
Thus whenever one employs the stability condition (20), the well-posedness condition (physical constraints) (14) can be guaranteed immediately by choosing
![]() (21)
(21)
6. Numerical Simulation
We implement the Lax-Friedrichs scheme by developing a computer programming code and perform numerical simulation as described below.
6.1. Error Estimation of the Numerical Scheme
In order to perform error estimation, we consider the exact solution (9) with initial condition![]() , we have
, we have
![]() (22)
(22)
We prescribe the corresponding two-sided boundary value by the equations
![]() (23)
(23)
And
![]() (24)
(24)
For the above initial and boundary conditions with vmax = 0.0167 km/sec = 60.12 km/hour; satisfying the physical constraint condition (21); ρmax = 5 maxiρ0(xi) = 550 vehicles/km in the spatial domain [5 km, 10 km] we perform the numerical experiment for 4 minutes in ![]() time steps for a highway of 10 km in 401 spatial grid points with step size
time steps for a highway of 10 km in 401 spatial grid points with step size ![]() which guarantees the stability condition (20);
which guarantees the stability condition (20); ![]() . We compute the relative error in L1-norm defined by
. We compute the relative error in L1-norm defined by
![]() (25)
(25)
for all time where ![]() is the exact solution and
is the exact solution and ![]() is the numerical solution computed by the Lax-Friedrich’s scheme.
is the numerical solution computed by the Lax-Friedrich’s scheme.
Figure 3(a) shows the relative error for Lax-Friedrich’s scheme. For Lax-Friedrich’s scheme, the relative error is less than or equal to 0.000046; which is quite acceptable. Figure 3(b) presents that the error is decreasing with respect to the smaller discretization parameters ![]() and
and ![]() ; which shows the convergence of the Lax- Friedrich’s scheme. We observe that, as we increase number of grid points the error is decreasing. Figure 3(b) shows the rate of convergence of the numerical solutions.
; which shows the convergence of the Lax- Friedrich’s scheme. We observe that, as we increase number of grid points the error is decreasing. Figure 3(b) shows the rate of convergence of the numerical solutions.
Now we consider the initial density using sine function and perform numerical computation in the spatial domain [0, 10] in km. Figure 4(a) shows the initial density and Figure 4(b) shows the initial density and the density after six minutes.
6.2. Comparative Profile of Density, Velocity and Flux
Figure 5(a) and Figure 5(b) respectively show the density ![]() profiles and velocity
profiles and velocity ![]() profiles for three different times and one can observe from the two figures that the density and velocity are maintaining the negative relation, as given by Equation (3), throughout the computational process as expected. Figure 5(c) shows the flux
profiles for three different times and one can observe from the two figures that the density and velocity are maintaining the negative relation, as given by Equation (3), throughout the computational process as expected. Figure 5(c) shows the flux ![]() profiles for three different times.
profiles for three different times.
![]() (a) (b)
(a) (b)
Figure 3. (a) Relative errors of Lax-Friedrich’s Scheme; (b) Convergence of errors of Lax-Friedrich’s Scheme.
![]() (a) (b)
(a) (b)
Figure 4. (a) Initial traffic density for 10 kilometer highway; (b) Comparative position of the cars between initial and six minutes.
Finally, Figure 6(a) presents the computed car velocity as a function of density which verifies the non-linear- velocity-density function as shown in Figure 1. Figure 6(b) shows the computed flux (traffic flow) as a function
![]() (a) (b)
(a) (b)![]() (c)
(c)
Figure 5. (a) Density profile for 3 minutes in 10 km highway; (b) Velocity profile for 3 minutes in 10 km highway; (c) Flux profile for 3 minutes in 10 km.
![]() (a) (b)
(a) (b)
Figure 6. (a) Non-linear velocity-density relationship; (b) Fundamental diagram of traffic flow model for non-linear velocity-density relationship.
of density which also verifies qualitative behavior, the well-known fundamental diagram as Figure 2.
7. Conclusion
The computational result obtained by implementing the analogous version of Lax-Friedrich’s scheme shows the accuracy up to five decimal places and a good rate of convergence. Performing numerical simulation, we have verified some qualitative traffic flow behavior for various traffic parameters. Finally, we have presented fundamental diagram of traffic flow using this scheme, which is a very good qualitative agreement of the Lax-Frie- drich’s scheme for traffic flow model. In our model, we have considered only single lane highway. The model can be extended for multi-lane traffic flow model which we leave as our future work.