1. Introduction
Let 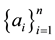 be a sequence of natural numbers
be a sequence of natural numbers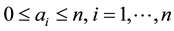 , and
, and  be an
be an 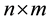 array associated with this sequence, whose entries
array associated with this sequence, whose entries 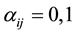 such that
such that
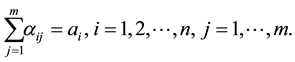
The path of order k along 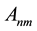 is defined to be a sequence of entries
is defined to be a sequence of entries 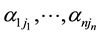 as follows
as follows
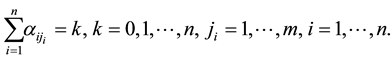
The number of paths of order k will be denoted by
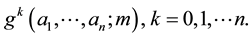
By neglecting the last row in 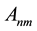 and then reconsidering it, we get the recurrence
and then reconsidering it, we get the recurrence
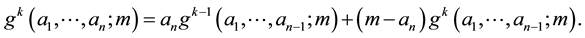 (1)
(1)
When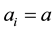 , a is a constant,
, a is a constant, ![]() then
then
![]() (2)
(2)
and
![]()
Khidr and El-Desouky [1] proved that, when ![]()
![]() (3)
(3)
where ![]() are the generalized Stirling numbers of the first kind associated with the sequence of real numbers
are the generalized Stirling numbers of the first kind associated with the sequence of real numbers![]() , defined by [1] - [6] ,
, defined by [1] - [6] ,
![]() (4)
(4)
These numbers satisfy the recurrence relation
![]() (5)
(5)
And
![]()
Moreover, they introduced a special case of (3), when![]() , then the number of paths of order k,
, then the number of paths of order k, ![]() is denoted by
is denoted by![]() ; and proved that
; and proved that
![]() (6)
(6)
where ![]() are the Stirling numbers of the first kind defined by, see [2] [3]
are the Stirling numbers of the first kind defined by, see [2] [3]
![]()
Also the generating function for ![]() is given by
is given by
![]() (7)
(7)
In this article, in Section 2, we derive a generalization of some results given in [1] , for the number of paths of
order k, ![]() , when
, when![]() . The generating function of
. The generating function of ![]() is given. In Section 3, we find the probability distribution for
is given. In Section 3, we find the probability distribution for ![]() and study some of their properties. The moment
and study some of their properties. The moment
generating function, skewness and kurtosis for ![]() are investigated. Moreover special case and numerical results are given in Section 4.
are investigated. Moreover special case and numerical results are given in Section 4.
2. Main Results
Theorem 1. The number of paths of order k is given by
![]() (8)
(8)
Proof. Using (5) in (8), we get
![]()
This by virtue of (1) completes the proof of (8).
Theorem 2. The generating function of the number of paths of order k is given by
![]() (9)
(9)
Proof. Let the generating function of the number of paths of order k be denoted by
![]() (10)
(10)
Using (1), we obtain
![]()
and hence we get
![]()
where![]() . This completes the proof.
. This completes the proof.
From (9), we get
![]()
where ![]() and hence we have
and hence we have
![]() (11)
(11)
where ![]()
For the special case![]() , we get
, we get
![]() (12)
(12)
where ![]()
From (6) and (12), we have the identity
![]() (13)
(13)
where ![]()
3. Some Applications
Let X, be the number of paths along![]() , then by virtue of (8) we have
, then by virtue of (8) we have
![]() (14)
(14)
On the other hand the moment generating function of the random variable X denoted by![]() , is given by the following theorem.
, is given by the following theorem.
Theorem 3. The moment generating function of X, is given by
![]() (15)
(15)
Proof. We begin by the definition of the moment generating function as follows.
![]()
This completes the proof.
Corollary 1. The jth moments of X is
![]() (16)
(16)
Proof. The jth moments can be obtained from the moment generating function, ![]() where
where
![]()
This completes the proof.
Then from (16), we can calculate the mean and variance for the random variable X as follows.
![]() (17)
(17)
![]() (18)
(18)
hence the variance is given by
![]() (19)
(19)
Corollary 2. The Skewness and kurtosis for the random variable X are given by
![]() (20)
(20)
where
![]()
![]()
![]()
Proof. We can find the jth moments about the mean by using
![]() (21)
(21)
From (16) and (21), we can find the moments ![]() about mean which can be used to calculate the skweness and kurtosis.
about mean which can be used to calculate the skweness and kurtosis.
Special Case:
If![]() , from (14), we have
, from (14), we have
![]()
and from (16) the jth moments has the form
![]()
and the mean is given by
![]()
![]()
the variance can be obtained as follows.
![]()
where we used![]() , see [3] .
, see [3] .
4. Numerical Results
Setting![]() . Therefore the numerical values of
. Therefore the numerical values of![]() , are reduced to
, are reduced to![]() , see [4] [5] .
, see [4] [5] .
From Equation (14), we can find the probability distribution of the number of paths X along ![]() as follows
as follows
From (16), we can compute the 4th moments as follows.
The 4th moments about mean can be obtained as
The values of mean and variance can be obtained from (17) and (19) as follows.
![]()
The skewness and kurtosis, respectively can be obtained from (20) as follows.
![]()