1. Introduction
A study by [1] on eigenvalue assignment for single-input linear systems is followed in this paper. It is based on the well-known entire eigenstructure assignment method [2] - [4] . A survey on the entire eigenstructure method has been conducted by [5] , and used by [6] for control system design. An algorithmic approach to eigenvalue assignment has been conducted by [7] , besides, partial assignment using orthogonality relations by [8] . In addition, studies regarding existence, uniqueness, and numerical solution have been conducted by [9] .
As required by this method, the w-eigenvectors and companion z-vectors are extracted out of the null space of an augmented 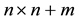 matrix .
matrix .
Basically, the method in [1] deals with a transformed system representation. It also avoids manipulating null spaces. Instead, it relies on explicit determination of the closed loop w-eigenvectors and the companion z-vec- tors of the transformed system. The determination process is systematic and conceptually simple. The components of the w-eigenvectors depend explicitly on the assigned eigenvalues and on the coefficients of the characteristic equation. The companion z-vectors turn out to be straightforward, being the open loop characteristic equation evaluated at the closed loop eigenvalues to be assigned.
The procedure in [1] has been applied to single-input controllable systems. In this paper, the method is revisited and shown to apply to uncontrollable systems equally well. Besides, the method has also been extended to deal with a particular case of multi-input systems. To achieve this, the transformation matrices have been modified accordingly to suit the uncontrollable case and the multi-input case. The case of repeated eigenvalues is also revisited, proving the facts established by demonstration in [1] . Furthermore, existence of the solution of the assigned closed loop eigenvectors is also proved.
For the single-input and multi-input cases, the study shows that calculations of the needed w-eigenvectors and the z-vectors are based on lower order matrices specifying the controllable part and the uncontrollable part of the system. Such approach simplifies the design process, and provides numerical advantages.
Finally, the two examples are worked out in Section 8 to illustrate the ease of use of the assignment process.
2. Basis of the Method
Consider the linear time-invariant system given by
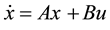 (2.1)
(2.1)
where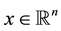 ,
, 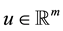 , and the rank of B is m. It is required to change the eigenvalues by states feedback using
, and the rank of B is m. It is required to change the eigenvalues by states feedback using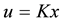 , where
, where 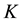 assigns
assigns 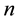 eigenvalues
eigenvalues 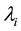 together with the corresponding
together with the corresponding 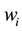 eigenvectors according to
eigenvectors according to
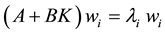 (2.2)
(2.2)
or
 (2.3)
(2.3)
Such setup as in (2.3) is associated in the control literature with the entire eigenstructure assignment method (see [2] [3] ).
It is assumed that the open loop characteristic equation is given by
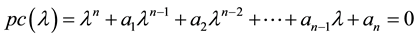 (2.4)
(2.4)
In the development of the explicit methods, a state transformation  is used where
is used where , and as has been shown in [1] , the
, and as has been shown in [1] , the  matrix needed is
matrix needed is
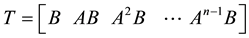 (2.5)
(2.5)
resulting in the system
![]() (2.6)
(2.6)
![]() (2.7)
(2.7)
A similar transformation will be used in this paper, together with the following rearrangement of (2.3) as
![]() (2.8)
(2.8)
Such rearrangement is preferable in order to avoid a mixture pluses and minuses in the resulting formulae.
3. The Uncontrollable Case
The design procedure outlined in [1] applies to controllable systems only. It will now be extended to the case of uncontrollable systems. It turns out that the same explicit w-eigenvectors and z-vectors determination still applies with the added advantage of manipulating lower order matrices and vectors. A transformation matrix T different from that in (2.5) should be used since that of (2.5) will not be invertible due to the uncontrollability of the system. The modified T assumes the following form.
![]() (3.1)
(3.1)
where q is the number of controllable eigenvalues and N is any ![]() matrix chosen to guarantee the nonsingularity of T. With this particular transformation the partitioned G and H matrices will assume the following forms.
matrix chosen to guarantee the nonsingularity of T. With this particular transformation the partitioned G and H matrices will assume the following forms.
![]() (3.2)
(3.2)
where ![]() and
and ![]() will retain the forms of (2.7) but of reduced dimension, that is
will retain the forms of (2.7) but of reduced dimension, that is
![]() (3.3)
(3.3)
where![]() ,
, ![]() is a
is a ![]() matrix representing the controllable part of the system,
matrix representing the controllable part of the system, ![]() and
and ![]() are
are ![]() and
and ![]() matrices respectively which depend on the particular choice of
matrices respectively which depend on the particular choice of![]() . Although ma-
. Although ma-
trix ![]() is not unique (depending on
is not unique (depending on![]() ), its eigenvalues are unique being equal to the uncontrollable eigenvalues.
), its eigenvalues are unique being equal to the uncontrollable eigenvalues.
4. Solutions by Decomposition of the Eigenvectors
It will now be shown that the calculation complexity can be eased through decomposing the closed loop eigenvectors into two vector parts. By doing so, reduced order matrices are dealt with, resulting in vector parts of dimension ![]() and
and![]() . The z-vector remains an
. The z-vector remains an ![]() vector. If the original method of calculation of the entire eigenstructure method were to be used [2] [3] , then vectors of dimension
vector. If the original method of calculation of the entire eigenstructure method were to be used [2] [3] , then vectors of dimension ![]() are determined for real eigenvector assignment, and vectors of dimension
are determined for real eigenvector assignment, and vectors of dimension ![]() are determined for the complex eigenvector assignment.
are determined for the complex eigenvector assignment.
Consider assignment of an eigenvalue ![]() which is not aneigenvalue of
which is not aneigenvalue of![]() , then the matrix
, then the matrix ![]() is nonsingular. Let the associated eigenvector be decomposed as
is nonsingular. Let the associated eigenvector be decomposed as
![]() (4.1)
(4.1)
where ![]() and
and ![]() are
are ![]() and
and ![]() vectors respectively. According to (2.8), and dealing with the transformed system, we solve
vectors respectively. According to (2.8), and dealing with the transformed system, we solve
![]() (4.2)
(4.2)
So
![]() (4.3)
(4.3)
Since ![]() is nonsingular then
is nonsingular then ![]() is necessarily the zero vector, also
is necessarily the zero vector, also
![]() (4.4)
(4.4)
Since ![]() multiplies
multiplies ![]() which is the zero vector then
which is the zero vector then ![]() has only to satisfy the reduced order equations given by
has only to satisfy the reduced order equations given by
![]() (4.5)
(4.5)
Equations in (4.5) are in the same format of as (3.3) where a solution always exists irrespective of ![]() (see Section 7). In which case, and provided
(see Section 7). In which case, and provided ![]() the solution of
the solution of![]() ,
, ![]() , and
, and![]() , are systematically obtained according to the explicit formulae as
, are systematically obtained according to the explicit formulae as
![]() (4.6)
(4.6)
![]() (4.7)
(4.7)
and
![]() (4.8)
(4.8)
Note that both solutions of ![]() and
and ![]() now depend on the coefficients of the reduced
now depend on the coefficients of the reduced ![]() order
order ![]() characteristic equation of the controllable subspace.
characteristic equation of the controllable subspace.
Consider now reassignment of an uncontrollable eigenvalue ![]() with an associated qualifying eigenvector, then the matrix
with an associated qualifying eigenvector, then the matrix ![]() is singular. Let the associated eigenvector be decomposed as in (4.1).
is singular. Let the associated eigenvector be decomposed as in (4.1).
One choice for ![]() is the zero vector, rendering the product
is the zero vector, rendering the product ![]() zero, in which case (4.4) becomes
zero, in which case (4.4) becomes
![]() (4.9)
(4.9)
Since ![]() and
and ![]() are in the form given in (3.3), then
are in the form given in (3.3), then ![]() is evaluated as in (4.7). According to (4.6),
is evaluated as in (4.7). According to (4.6), ![]() is calculated through the reduced order characteristic equation of the controllable part evaluated at the uncontrollable eigenvalue.
is calculated through the reduced order characteristic equation of the controllable part evaluated at the uncontrollable eigenvalue.
A second choice is that ![]() is non-zero, given by the matrix representation of the null space of
is non-zero, given by the matrix representation of the null space of![]() , in which case,
, in which case, ![]() is obtained through the solution of
is obtained through the solution of
![]() (4.10)
(4.10)
Since ![]() is already calculated as mentioned above, and when
is already calculated as mentioned above, and when ![]() is nonsingular, the solution for
is nonsingular, the solution for ![]() is given by.
is given by.
![]() (4.11)
(4.11)
The arbitrariness in ![]() is due to the arbitrariness in choosing
is due to the arbitrariness in choosing ![]() and in whatever arbitrariness is available in the null space of
and in whatever arbitrariness is available in the null space of![]() .
.
This second choice is a must when using the entire eigenstructure assignment method. If ![]() is a zero vector then the W matrix of the n closed loop eigenvectors will be singular. Obviously this should be avoided as
is a zero vector then the W matrix of the n closed loop eigenvectors will be singular. Obviously this should be avoided as ![]() implies an invertible W matrix.
implies an invertible W matrix.
It is worth mentioning that an eigenvector corresponding to an uncontrollable eigenvalue can be tailored out of the two possible ones stemming from the two choices.
Finally, having obtained n independent eigenvectors ![]() with companion z- vectors
with companion z- vectors![]() , the state feedback matrix determined by the entire eigenstructure method in the original state space representation is
, the state feedback matrix determined by the entire eigenstructure method in the original state space representation is![]() , i.e.
, i.e.
![]() (4.12)
(4.12)
5. A Multi-Input Case
The explicit nature of the method can be extended to a multi-input case. This is possible in the case where matrices A and B have a particular structure which results in the following augmented matrix
![]() (5.1)
(5.1)
To be an nxn square and nonsingular, where ![]() is such that
is such that![]() .
.
To prove such assertion, use the same similarity transformation ![]() with t as in (5.1), giving.
with t as in (5.1), giving.
![]() (5.2)
(5.2)
where ![]() are square submatrices of order m. Let the eigenvalues assigned be that of the
are square submatrices of order m. Let the eigenvalues assigned be that of the ![]() matrix
matrix![]() . Invoking (2.3), with A replaced by G, and B by H, we get
. Invoking (2.3), with A replaced by G, and B by H, we get
![]() (5.3)
(5.3)
The following proof is straightforward, achieved by substituting generalized matrix forms for the w-eigen- vectors and z-vectors in (5.3). It is presented for the case![]() . In analogy with the single-input case with careful attention now to the order of matrix multiplication (i.e.
. In analogy with the single-input case with careful attention now to the order of matrix multiplication (i.e. ![]() postmultiplies other submatrices), and provided the last
postmultiplies other submatrices), and provided the last ![]() submatrix of
submatrix of ![]() is normalized to
is normalized to![]() , the solutions
, the solutions ![]() and
and ![]() are
are
![]() (5.4)
(5.4)
and
![]() (5.5)
(5.5)
Note that the z-vectors ![]() are now given through what may be called a generalized reduced order characteristic equation.
are now given through what may be called a generalized reduced order characteristic equation.
The nested nature of the solutions is imminent, easily generalized for cases where![]() . Note that a
. Note that a ![]() either specifies a single eigenvalue, in which case we get
either specifies a single eigenvalue, in which case we get ![]() independent eigenvectors to choose from, or it specifies m distinct eigenvalues in which case we get a single eigenvector corresponding to an eigenvalue. Besides, a real-element
independent eigenvectors to choose from, or it specifies m distinct eigenvalues in which case we get a single eigenvector corresponding to an eigenvalue. Besides, a real-element ![]() can be used to assign complex eigenvalues whenever the number m caters for that.
can be used to assign complex eigenvalues whenever the number m caters for that.
The extension of the assignment to multi-input uncontrollable systems is also straightforward. The number of the uncontrollable eigenvalues should be an integer multiple of ![]() in this case. If their number is
in this case. If their number is ![]() then matrices T, G, and H assume the following forms.
then matrices T, G, and H assume the following forms.
![]() (5.6)
(5.6)
![]() (5.7)
(5.7)
The same theory developed in Section 4 still applies. The uncontrollable eigenvalues are those of![]() .
. ![]() will be a
will be a ![]() zero matrix, and
zero matrix, and ![]() will be diagonal or a Jordan form if matrix N is a basis of the span of the uncontrollable subspsce.
will be diagonal or a Jordan form if matrix N is a basis of the span of the uncontrollable subspsce.
6. Repeated Eigenvalues
In [1] , it has been demonstrated that the z-vectors associated with the repeated eigenvalues can be obtained by successive differentiation of the basic z-vector .It remains to prove this property irrespective of the transformation used.
Consider the general setup of the entire eigenstructure assignment as formulated in (2.2). Let there be p identical eigenvalues ![]() together with their associated eigenvectors
together with their associated eigenvectors![]() , and let
, and let ![]() be the basic first eigenvector , hence
be the basic first eigenvector , hence
![]() (6.1)
(6.1)
and
![]() (6.2)
(6.2)
To facilitate the proof, a convenient rearrangement for ![]() and
and ![]() is
is
![]() (6.3)
(6.3)
![]() (6.4)
(6.4)
Differentiating (6.3) with respect to![]() , we get
, we get
![]() (6.5)
(6.5)
Comparing (6.4) with (6.5), we infer
![]() (6.6)
(6.6)
Similarly, differentiating (6.4) with respect to![]() , we get
, we get
![]() (6.7)
(6.7)
or
![]() (6.8)
(6.8)
Comparing (6.8) with (6.9)
![]() (6.9)
(6.9)
We get
![]() (6.10)
(6.10)
Repeating the same process, it can be shown that
![]() (6.11)
(6.11)
or
![]() (6.12)
(6.12)
Confirming what has been demonstrated in [1] . Such differential properties regarding the w-eigenvectors and z-vectors are pertinent to the vectors irrespective of the transformation used.
7. Existence of the Solution
It’s worth considering the existence of the solutions when considering the controllable and uncontrollable subspaces. For the controllable subspace, we seek the solution ![]() where
where
![]() (7.1)
(7.1)
For the solution of![]() , using (7.1)
, using (7.1)
![]() (7.2)
(7.2)
If ![]() is not an eigenvalue of
is not an eigenvalue of![]() , then
, then ![]() is nonsingular and the solution always exists. Otherwise,
is nonsingular and the solution always exists. Otherwise, ![]() is an eigenvalue of
is an eigenvalue of ![]() and
and ![]() is singular, and for a solution to exists the following condition should hold [10] -[13] .
is singular, and for a solution to exists the following condition should hold [10] -[13] .
![]() (7.3)
(7.3)
Alternatively,
![]() (7.4)
(7.4)
i.e. ![]() can be expressed as a linear combination of scalar multiples of the columns of
can be expressed as a linear combination of scalar multiples of the columns of![]() . For the case
. For the case![]() , the following combination of the left hand columns gives,
, the following combination of the left hand columns gives,
![]() (7.5)
(7.5)
i.e. (7.4) holds. Hence, a solution always exists irrespective of ![]() assigned.
assigned.
For the uncontrollable subspace
![]() (7.6)
(7.6)
Since the right hand side is zero the condition in (7.4) always holds and the solution always exists given by a matrix representation of the null space of![]() .
.
8. Examples
Example 1
An uncontrollable system has the following system matrices
![]() (8.1)
(8.1)
The system is unstable having eigenvalues 1, −1, −2, and −3. It is required to assign the eigenvalues −3, −4, −5, and of course to reassign the uncontrollable eigenvalue −2.
The similarity transformation used is
![]() (8.2)
(8.2)
Leading to G and H matrices
![]() (8.3)
(8.3)
As evident by the system after transformation, −2 is the uncontrollable eigenvalue, and that the controllable subspace has the matrix representation as that of (3.3).
Hence, the reduced order characteristic equation is
![]() (8.4)
(8.4)
Utilizing explicit determination, the closed loop eigenvector corresponding to the −2 eigenvalue is calculated using (4.11), the remaining ones using (4.7), and the companion z-vector using (4.6) where ![]() giving.
giving.
![]() (8.5)
(8.5)
![]() (8.6)
(8.6)
In order to have a nonsingular W matrix, the eigenvector ![]() associated with the uncontrollable eigenvalue has been calculated according to the second choice with
associated with the uncontrollable eigenvalue has been calculated according to the second choice with![]() , then scaled to have its elements as integers..
, then scaled to have its elements as integers..
According to (4.12), the state feedback matrix in the original system representation is
![]() (8.7)
(8.7)
N.B.; The state feedback matrix above assigns the four eigenvalues required according to the entire eigenstructure method. If the answer is to be checked using any other method like the Matlab place function, a different result for K may be obtained. This is due to the fact that K for uncontrollable systems is not unique.
Example 2
Consider an unstable multi-input system having the following A and B matrices
![]() (8.8)
(8.8)
using the transformation![]() , one gets
, one gets
![]() (8.9)
(8.9)
Hence,
![]() (8.10)
(8.10)
Let the eigenvalues assigned be![]() , with assigned eigenvector
, with assigned eigenvector ![]() and associated z-vectors
and associated z-vectors ![]() respectively. One choice for
respectively. One choice for ![]() are
are
![]() (8.11)
(8.11)
Using the formulae given in (5.4) the closed loop eigenvectors are calculated pair-wise, i.e. ![]() , and are respectively
, and are respectively
![]() (8.12)
(8.12)
The companion z-vectors ![]() are calculated using (5.5) and are respectively
are calculated using (5.5) and are respectively
![]() (8.13)
(8.13)
According to (4.12) with ![]() being now column vectors, the feedback matrix K, is
being now column vectors, the feedback matrix K, is
![]() (8.14)
(8.14)
Note that Matlab calculates in double precision, however, format short of matlab has been used in the print out of the above results. So, to check the results, one may have to go through the calculations once more in case the precision of K provided in (8.14) is not adequate.
9. Conclusion
The study has shown that the explicit methods can be extended to uncontrollable systems just as easy with the benefit of dealing with lower order matrices, and consequently with reduced w-eigenvectors. The z-vectors are also determined using lower order characteristic equations and shown to bear a differentiation property for the repeated eigenvalues case. For the uncontrollable case, it turns out that the z-vectors have more degrees of freedom which can be used to shape the system response. The methods can also be extended to a special case of multi-input controllable and uncontrollable systems. The solutions of the w-eigenvectors and the z-vectors are always guaranteed. The two examples demonstrate the ease of application of the formulae in the design of state feedback matrices.