Exact Quasi-Classical Asymptotic beyond Maslov Canonical Operator and Quantum Jumps Nature ()
1. Introduction
A number of experiments on trapped single ions or atoms have been performed in recent years [1] - [4] . Monitoring the intensity of scattered laser light off of such systems has shown abrupt changes that have been cited as evidence of “quantum jumps” between states of the scattered ion or atom. The existence of such jumps was required by Bohr in his theory of the atom. Bohr’s quantum jumps between atomic states [5] were the first form of quantum dynamics to be postulated. He assumed that an atom remained in an atomic eigenstate until it made an instantaneous jump to another state with the emission or absorption of a photon. Since these jumps do not appear to occur in solutions of the Schrodinger equation, something similar to Bohr’s idea has been added as an extra postulate in modern quantum mechanics.
Stochastic quantum jump equations [6] - [8] were introduced as a tool for simulating the dynamics of a dissipative system with a large Hilbert space and their links with quantum measurement theory were also noted [9] - [13] . This measurement interpretation is generally known as quantum trajectory theory [14] . By adding filter cavities as part of the apparatus, even the quantum jumps in the dressed state model can be interpreted as approximations to measurement-induced jumps [15] .
The question arises whether an explanation of these jumps can be found to result from a Colombeau solution [16] - [18] 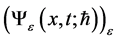 of the Schrödinger equation alone without additional postulates. We found exact quasi-classical asymptotic of the quantum averages with position variable with localized initial data.
of the Schrödinger equation alone without additional postulates. We found exact quasi-classical asymptotic of the quantum averages with position variable with localized initial data.
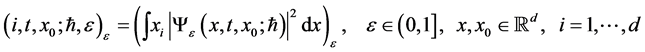 (1.1)
(1.1)
i.e. we found the limiting Colombeau quantum averages (limiting Colombeau quantum trajectories) such that [18] :
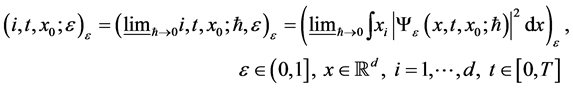 (1.2)
(1.2)
and limiting quantum trajectories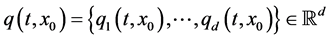 ,
, 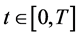 such that
such that
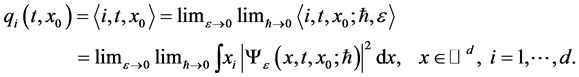 (1.3)
(1.3)
if limit in LHS of Equation (1.3) exists.
The physical interpretation of these asymptotic given below, shows that the answer is “yes” for the limiting quantum trajectories with localized initial data.
Note that an axiom of quantum measurement is: if the particle is in some state 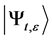 that the probability
that the probability  of getting a result
of getting a result 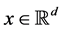 at instant
at instant  with an accuracy of
with an accuracy of 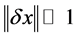 will be given by
will be given by
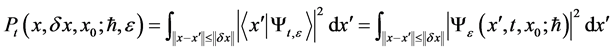 . (1.4)
. (1.4)
We rewrite now Equation (1.4) of the form
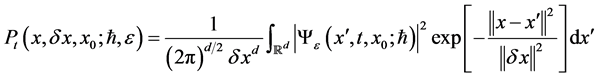 (1.5)
(1.5)
We define well localized limiting quantum trajectories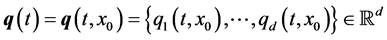 ,
,
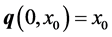 ,
, 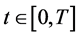 such that:
such that:
![]() (1.6)
(1.6)
and well localized limiting quantum trajectories![]() ,
, ![]() ,
, ![]() such that:
such that:
![]() (1.7)
(1.7)
if limit in LHS of Equation (1.7) exists.
2. Colombeau Solutions of the Schrödinger Equation and Corresponding Path Integral Representation
Let ![]() be a complex infinite dimensional separable Hilbert space, with inner product
be a complex infinite dimensional separable Hilbert space, with inner product ![]() and norm
and norm![]() .
.
Let us consider Schrödinger equation:
![]() , (2.1)
, (2.1)
![]() . (2.2)
. (2.2)
Here operator ![]() is essentially self-adjoint,
is essentially self-adjoint, ![]() is the closure of
is the closure of![]() .
.
Theorem 2.1. [19] [20] . Assume that: (1)![]() , (2)
, (2) ![]() is continuous and
is continuous and
![]() . Then corresponding solution of the Schrödinger Equations (2.1)-(2.2) exist and can be represented via formulae
. Then corresponding solution of the Schrödinger Equations (2.1)-(2.2) exist and can be represented via formulae
![]() , (2.3)
, (2.3)
where we have set ![]() and
and
![]() , (2.4)
, (2.4)
where![]() , Let
, Let ![]() be a trajectory; that is, a function from
be a trajectory; that is, a function from ![]() to
to ![]() with
with ![]() and set
and set
![]() ,
,![]() . We rewrite Equation (2.3) for a future application symbolically for short of the following form
. We rewrite Equation (2.3) for a future application symbolically for short of the following form
![]() , (2.5)
, (2.5)
where we have set 1) ![]() and 2)
and 2) ![]() that is, a
that is, a
![]() , (2.6)
, (2.6)
Trotter and Kato well known classical results give a precise meaning to the Feynman integral when the potential ![]() is sufficiently regular [18] [19] . However if potential
is sufficiently regular [18] [19] . However if potential ![]() is a non-regular this is well known problem to represent solution of the Schrödinger Equations (2.1)-(2.2) via formulae (2.3), see [19] .
is a non-regular this is well known problem to represent solution of the Schrödinger Equations (2.1)-(2.2) via formulae (2.3), see [19] .
We avoided this difficulty using contemporary Colombeau framework [16] - [18] . Using replacement
![]() ,
, ![]() ,
, ![]() we obtain from potential
we obtain from potential ![]() regularized
regularized
Potential![]() ,
, ![]() such that
such that ![]() and
and
1)![]() ,
,
![]() . (2.7)
. (2.7)
Here ![]() is Colombeau algebra of Colombeau generalized functions [16] - [18] .
is Colombeau algebra of Colombeau generalized functions [16] - [18] .
Finally we obtain regularized Schrödinger equation of Colombeau form [21] - [24] :
![]() , (2.8)
, (2.8)
![]() . (2.9)
. (2.9)
Using the inequality (2.7) Theorem 2.1 asserts again that corresponding solution of the Schrödinger Equations (2.8)-(2.9) exist and can be represented via formulae:
![]() , (2.10)
, (2.10)
where we have set ![]() and
and
![]() , (2.11)
, (2.11)
where we have set![]() .
.
We rewrite Equation (2.10) for a future application symbolically of the following form
![]() , (2.12)
, (2.12)
or of the following form
![]() . (2.13)
. (2.13)
For the limit in RHS of (2.12) and (2.13) we will be used canonical path integral notation
![]() , (2.14)
, (2.14)
where![]() .
.
Substitution ![]() into RHS of the Equation (2.10) gives
into RHS of the Equation (2.10) gives
![]() .
.
(2.15)
We rewrite Equation (2.15) for a future application symbolically of the following form
![]() , (2.16)
, (2.16)
or of the following form
![]() . (2.17)
. (2.17)
For the limit in RHS of (2.16) and (2.17) we will be used following path integral notation
![]() . (2.18)
. (2.18)
Let us consider now regularized oscillatory integral
![]() . (2.19)
. (2.19)
Lemma 2.1. (Localization Principle [25] [26] ) Let ![]() be a domain in
be a domain in ![]() and
and ![]() be a smooth function of compact support,
be a smooth function of compact support, ![]() ,
, ![]() be a real valued smooth function without stationary points in
be a real valued smooth function without stationary points in![]() , i.e.
, i.e. ![]() for
for![]() . Let
. Let ![]() be a differential operator
be a differential operator
![]() . (2.20)
. (2.20)
Then ![]() there exist
there exist ![]() such that
such that
![]() . (2.21)
. (2.21)
Lemma 2.2. (Generalized Localization Principle) Let ![]() be a domain in
be a domain in ![]() and
and ![]() be a real valued smooth function without stationary points in
be a real valued smooth function without stationary points in![]() , i.e.
, i.e. ![]() for
for ![]() and let
and let ![]() be infinite sequence
be infinite sequence![]() :
:
![]() . (2.22)
. (2.22)
Then there exist infinite sequence![]() ,
, ![]() such that
such that
![]() .
.
Proof. Equality (2.23) immediately follows from (2.21).
Remark 2.1. From Lemma 2.2 follows that stationary phase approximation is not a valid asymptotic approximation in the limit ![]() for a path-integral (2.14) and (2.18).
for a path-integral (2.14) and (2.18).
3. Exact Quasi-Classical Asymptotic Beyond Maslov Canonical Operator
Theorem 3.1. Let us consider Cauchy problem (2.8) with initial data ![]() is given via formula
is given via formula
![]() , (3.1)
, (3.1)
where ![]() and
and![]() .
.
1) We assume now that: a)![]() , b)
, b) ![]() and c)
and c) ![]() function
function ![]() is a polynomial on variable
is a polynomial on variable![]() , i.e.
, i.e.
![]() . (3.2)
. (3.2)
2) Let ![]() be the solution of the boundary problem
be the solution of the boundary problem
![]() , (3.3)
, (3.3)
![]() . (3.4)
. (3.4)
Here![]() ,
, ![]() ,
,
![]() . (3.5)
. (3.5)
3) Let ![]() be the master action given via formula
be the master action given via formula
![]() , (3.6)
, (3.6)
where master Lagrangian ![]() are
are
![]() , (3.7)
, (3.7)
![]() . (3.8)
. (3.8)
Let ![]() be solution of the linear system of the algebraic equations
be solution of the linear system of the algebraic equations
![]() . (3.9)
. (3.9)
4) Let ![]() be solution of the linear system of the algebraic equations
be solution of the linear system of the algebraic equations
![]() . (3.10)
. (3.10)
Assume that: for a given values of the parameters ![]() the point
the point ![]() is not a focal point on a corresponding trajectory is given by corresponding solution of the boundary problem (3.3). Then for the limiting quantum average given via formulae (1.1) the inequalities is satisfied:
is not a focal point on a corresponding trajectory is given by corresponding solution of the boundary problem (3.3). Then for the limiting quantum average given via formulae (1.1) the inequalities is satisfied:
![]() . (3.11)
. (3.11)
Thus one can to calculate the limiting quantum trajectory corresponding to potential ![]() by using transcendental master equation
by using transcendental master equation
![]() . (3.12)
. (3.12)
Proof. From inequality (A.15) and Theorem A1, using inequalities (A.53.a) and (A.53.b) we obtain
![]() , (3.13)
, (3.13)
where
![]() , (3.14)
, (3.14)
![]() . (3.15)
. (3.15)
We note that
![]() , (3.16)
, (3.16)
where
![]() (3.17)
(3.17)
![]() (3.18)
(3.18)
and
![]() (3.19)
(3.19)
![]() . (3.20)
. (3.20)
From Equation (3.18) one obtain
![]() , (3.21)
, (3.21)
where
![]() , (3.22)
, (3.22)
![]() . (3.23)
. (3.23)
Let us calculate now path integral ![]() and path integral
and path integral![]() , using stationary phase approximation. From Equation (A.23) follows directly that action
, using stationary phase approximation. From Equation (A.23) follows directly that action ![]() coincide with master action
coincide with master action ![]() is given via formulae (3.6)-(3.8) and therefore from Equation (3.22) and Equation (3.23) one obtain
is given via formulae (3.6)-(3.8) and therefore from Equation (3.22) and Equation (3.23) one obtain
![]() (3.24)
(3.24)
and
![]() (3.25)
(3.25)
From Equation (3.17) and Equation (3.24) we obtain
![]() . (3.26)
. (3.26)
Substitution Equation (3.25) into Equation (3.26) gives
![]() . (3.26')
. (3.26')
Similarly one obtain
![]() . (3.27)
. (3.27)
Let us calculate now integral ![]() and integral
and integral ![]() using stationary phase approximation. Let
using stationary phase approximation. Let ![]() be the stationary point of master action
be the stationary point of master action ![]() and therefore Equation (3.9) is satisfied. Having applied stationary phase approximation one obtain
and therefore Equation (3.9) is satisfied. Having applied stationary phase approximation one obtain
![]() , (3.28)
, (3.28)
![]() . (3.29)
. (3.29)
Substitution Equations (3.28)-(3.29) into Equation (3.21) gives
![]()
(3.30)
Substitution Equation (3.30) into Equation (3.16) gives
![]() (3.31)
(3.31)
Similarly one obtain
![]() (3.32)
(3.32)
Therefore
![]() . (3.33)
. (3.33)
Substitution Equation (3.1) into Equation (3.33) gives
![]() . (3.34)
. (3.34)
Let us calculate now integral (3.34) using Laplace’s approximation. It is easy to see that corresponding stationary point ![]() is the solution of the linear system of the algebraic Equation (3.10). Therefore finally we obtain
is the solution of the linear system of the algebraic Equation (3.10). Therefore finally we obtain
![]() . (3.35)
. (3.35)
Substitution Equation (3.35) into inequality (3.13) gives the inequality (3.11). The inequality (3.11) completed the proof.
4. Quantum Anharmonic Oscillator with a Cubic Potential Supplemented by Additive Sinusoidal Driving
In this subsection we calculate exact quasi-classical asymptotic for quantum anharmonic oscillator with a cubic potential supplemented by additive sinusoidal driving. Using Theorem 3.1 we obtain corresponding limiting quantum trajectories given via Equation (1.3).
Let us consider quantum anharmonic oscillator with a cubic potential
![]() . (4.1)
. (4.1)
Supplemented by an additive sinusoidal driving. Thus
![]() . (4.2)
. (4.2)
The corresponding master Lagrangian given by (3.7), are
![]() . (4.3)
. (4.3)
We assume now that: ![]() and rewrite (4.3) of the form
and rewrite (4.3) of the form
![]() . (4.4)
. (4.4)
where ![]() and
and![]() .
.
The corresponding master action ![]() given by Equation (3.6), are
given by Equation (3.6), are
![]() (4.5)
(4.5)
The linear system of the algebraic Equation (3.9) are
![]() (4.6)
(4.6)
Therefore
![]() . (4.7)
. (4.7)
The linear system of the algebraic Equation (3.10) are
![]() . (4.8)
. (4.8)
Therefore the solution of the linear system of the algebraic Equation (3.10) are
![]() . (4.9)
. (4.9)
Transcendental master Equation (3.11) are
![]() (4.10)
(4.10)
Finally from Equation (4.10) one obtain
![]() . (4.11)
. (4.11)
where![]() .
.
Numerical Examples
Example 1 (in Figure 1 and Figure 2).![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
5. Comparison Exact Quasi-Classical Asymptotic with Stationary-Point Approximation
We set now![]() . Let us consider now path integral (2.14) with
. Let us consider now path integral (2.14) with ![]() given via formula
given via formula
![]() . (5.1)
. (5.1)
![]()
Figure 1. Limiting quantum trajectory ![]() with a jump.
with a jump.
![]()
Figure 2. Limiting quantum trajectory ![]() with a jump.
with a jump.
Note that for corresponding propagator ![]() the time discretized path-integral representation
the time discretized path-integral representation ![]() are:
are:
![]() , (5.2)
, (5.2)
where ![]() are:
are:
![]() . (5.3)
. (5.3)
Here the initial-![]() and end-points
and end-points ![]() are fixed by the prescribed
are fixed by the prescribed ![]() and by the additional constraint
and by the additional constraint![]() .
.
Let us calculate now integral (5.2) using stationary-point approximation. Denoting an critical points of the discrete-time action (5.3) by ![]() it follows that
it follows that ![]() satisfies the critical point conditions are
satisfies the critical point conditions are
![]() (5.4)
(5.4)
for![]() , supplemented by the prescribed boundary conditions for
, supplemented by the prescribed boundary conditions for![]() ,
, ![]() ,
,![]() .
.
From Equation (5.2) in the limit ![]() using formally stationary-point approximation one obtain
using formally stationary-point approximation one obtain
![]() . (5.5)
. (5.5)
Here the pre-factor ![]() is given via N-dimensional Gaussian integral of the canonical form as
is given via N-dimensional Gaussian integral of the canonical form as
![]() . (5.6)
. (5.6)
The Gaussian integral in (5.6) is given via canonical formula
![]() . (5.7)
. (5.7)
Here ![]() denote the determinant of an
denote the determinant of an ![]() matrix with elements
matrix with elements![]() .
.
Let us consider now Cauchy problem (2.8) with initial data ![]() is given via formula
is given via formula
![]() .
.
Note that for corresponding Colombeau solution ![]() given via path-integral (2.14) the time discretized path-integral representation
given via path-integral (2.14) the time discretized path-integral representation ![]() are
are
![]() (5.8)
(5.8)
Let us calculate now integrals in RHS of Equation (5.8) using stationary-point approximation. Corresponding critical point conditions are
![]() . (5.9)
. (5.9)
From (5.8) we obtain
![]() . (5.10)
. (5.10)
![]() . (5.11)
. (5.11)
Let as denote ![]() the critical point for which the critical point conditions (5.4) are
the critical point for which the critical point conditions (5.4) are
![]() . (5.12)
. (5.12)
Therefore the time discretized path-integral representation of the Colombeau quantum averages given by Equation (1.1) are
![]()
(5.13)
where![]() ,
, ![]() ,
,![]() . Let us calculate now integrals in RHS of Equation (5.13) using stationary- point approximation. Corresponding critical point conditions are
. Let us calculate now integrals in RHS of Equation (5.13) using stationary- point approximation. Corresponding critical point conditions are
![]() , (5.14)
, (5.14)
![]() . (5.15)
. (5.15)
Here ![]() can be calculated using linear recursion (5.12) with initial data
can be calculated using linear recursion (5.12) with initial data![]() .
.
From Equations (5.13)-(5.14) one obtain
![]() , (5.16)
, (5.16)
and![]() . (5.17)
. (5.17)
As demonstrated in [24] the determinant appearing in (5.11) can be calculated using second order linear recursion:
![]() (5.18)
(5.18)
with initial data![]() ,
,![]() (5.19)
(5.19)
from which the pre-factor![]() in (5.16) follows as
in (5.16) follows as
![]() . (5.20)
. (5.20)
In the limit ![]() from critical point conditions (5.12) and (5.14) one obtain
from critical point conditions (5.12) and (5.14) one obtain
![]() . (5.21)
. (5.21)
In the limit ![]() from a second order linear recursion (5.18) one obtain the second order linear differential equation
from a second order linear recursion (5.18) one obtain the second order linear differential equation
![]() (5.22)
(5.22)
with initial data
![]() . (5.23)
. (5.23)
By integration Equation (5.22) one obtain the first order linear differential equation
![]() . (5.24)
. (5.24)
In the limit ![]() from Equation (5.16), Equations (5.20)-(5.21) and Equation (5.24) one obtain
from Equation (5.16), Equations (5.20)-(5.21) and Equation (5.24) one obtain
![]() . (5.25)
. (5.25)
We set now in Equation (5.1)
![]() . (5.26)
. (5.26)
Corresponding differential master equation are
![]() . (5.27)
. (5.27)
From Equation (5.27) one obtain that corresponding transcend dental master equation are
![]() (5.28)
(5.28)
Numerical Examples
Comparison of the: 1) classical dynamics calculated by using Equation (5.1) (red curve), 2) limiting quantum trajectory ![]() calculated by using master equation Equation (5.28) (blue curve) and 3) limiting quantum trajectory calculated by using stationary-point approximation given by Equation (5.25) (green curve) (in Figure 3 and Figure 4).
calculated by using master equation Equation (5.28) (blue curve) and 3) limiting quantum trajectory calculated by using stationary-point approximation given by Equation (5.25) (green curve) (in Figure 3 and Figure 4).
![]()
Figure 3. Limiting quantum trajectory ![]() without jumps a = 0.3, b = 1, A = 2.
without jumps a = 0.3, b = 1, A = 2.
![]()
Figure 4. Limiting quantum trajectory ![]() with a jump a = 1, b = 1, A = 0.3.
with a jump a = 1, b = 1, A = 0.3.
6. Conclusions
We pointed out that there existed limiting quantum trajectories given via Equation (1.3) with a jump. Such jump does not depend on any single measurement of particle position ![]() at instant
at instant ![]() and is obtained without any reference to a phenomenological master-equation in Lindblad’s form.
and is obtained without any reference to a phenomenological master-equation in Lindblad’s form.
An axiom of quantum mechanics is that we cannot predict the result of any single measurement of an observable of a quantum mechanical system in a superposition of eigenstates. However we can predict the result of any single measurement of particle position ![]() at instant
at instant ![]() with a probability
with a probability ![]() if valid the condition:
if valid the condition:![]() , where
, where ![]() is given by Equation (1.5).
is given by Equation (1.5).
Acknowledgements
A reviewer provided important clarification.
Appendix
Let us consider now regularized Feynman-Colombeau propagator ![]() given by Feynman path integral:
given by Feynman path integral:
![]() , (A.1)
, (A.1)
where![]() ,
,
![]() , (A.2)
, (A.2)
![]() , (A.3)
, (A.3)
![]() (A.4)
(A.4)
![]() (A.5)
(A.5)
![]() , (A.6)
, (A.6)
![]() ,
,
![]() , (A.7)
, (A.7)
![]() . (A.8)
. (A.8)
Here:1)![]() ,
, ![]() and 2) for each path q(t) such that
and 2) for each path q(t) such that![]() ,
,
![]() ,
, ![]() , where
, where ![]() is a given function, operator
is a given function, operator ![]() are
are
![]() . (A.9)
. (A.9)
3) ![]() is a positive Feynman “measure”.
is a positive Feynman “measure”.
Therefore regularized Colombeau solution of the Schrödinger equation corresponding to regularized propagator (A.1) are
![]() (A.10)
(A.10)
Here![]() . (A.11)
. (A.11)
Let us consider now regularized quantum average
![]() . (A.12)
. (A.12)
From (A.5) and (A.12) one obtain
![]() (A.13)
(A.13)
From Equations (A.5)-(A.13) one obtain
![]() (A.14)
(A.14)
Using replacement![]() ,
, ![]() into RHS of the Equation (A.9) one obtain
into RHS of the Equation (A.9) one obtain
![]() (A.15)
(A.15)
Here
![]() (A.16)
(A.16)
And
![]() (A.17)
(A.17)
![]() (A.18)
(A.18)
Let us rewrite a function ![]() in the following equivalent form:
in the following equivalent form:
![]() , (A.19)
, (A.19)
![]() , (A.20)
, (A.20)
![]() , (A.21)
, (A.21)
where![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Let use valuate now path integral ![]() given via Equation (A.17). Substitution Equation (A.19) into RHS of the Equation (A.17) gives
given via Equation (A.17). Substitution Equation (A.19) into RHS of the Equation (A.17) gives
![]() ,
,
(A.22.a)
![]() ,
,
(A.22.b)
where
![]() , (A.23)
, (A.23)
![]() , (A.24)
, (A.24)
![]()
(A.25.a)
![]()
(A.25.b)
![]()
(A.26.a)
![]()
(A.26.b)
Let us evaluate now n-dimensional path integral![]() :
:
![]()
(A.27)
From Equation (A.27) one obtain the inequality
![]() (A.28)
(A.28)
From In Equation (A.28) one obtain the inequality
![]() (A.29)
(A.29)
where
![]() , (A.30)
, (A.30)
![]() . (A.31)
. (A.31)
Using replacement![]() ,
, ![]() ,
, ![]() into RHS of the Equation (A.31) one obtain
into RHS of the Equation (A.31) one obtain
![]()
(A.32)
![]() ,
, ![]() ,
, ![]() , see Equation (3.1) and
, see Equation (3.1) and
![]() , (A.33)
, (A.33)
![]() . (A.34)
. (A.34)
![]() . (A.35)
. (A.35)
From (A.29)-(A.35) one obtain
![]() (A.36)
(A.36)
![]() . (A.37)
. (A.37)
Proposition A.1. [27] [28] Let![]() be a double sequence
be a double sequence![]() . Let
. Let![]() .
.
Then the iterated limit:![]() exist and equal to
exist and equal to ![]() if and only if
if and only if ![]() exists for each
exists for each![]() .
.
Proposition A.2. Let![]() , where
, where ![]() is given via Eq-
is given via Eq-
uation (A.25) and let![]() , where
, where ![]() is given via Equa-
is given via Equa-
tion (A.26). Then
1) ![]()
2)![]() ,
,
3)![]() ,
,
4) ![]()
5)![]() ,
,
6)![]() .
.
Here
![]() ,
,
![]() .
.
Proof (I) Let us to choose an sequence ![]() such that
such that
1) ![]() and
and
2)![]() .
.
We note that from (ii) follows that: perturbative expansion
![]()
vanishes in the limit![]() . From (A.36) and Schwarz’s inequality using Proposition A.1, one obtain
. From (A.36) and Schwarz’s inequality using Proposition A.1, one obtain
![]() (A.38)
(A.38)
Let us to choose now an subsequence ![]() such that the limit:
such that the limit: ![]()
exist and![]() , (A.39)
, (A.39)
From (A.39) and Proposition A.1 one obtain
![]() . (A.40)
. (A.40)
From (A.39), (A.40) and (A.38) one obtain
![]() (A.41)
(A.41)
The inequality (A.41) completed the proof of the statement (1).
(II) Let us estimate now n-dimensional path integral
![]() (A.42)
(A.42)
From Equation (A.42) one obtain the inequality
![]() (A.43)
(A.43)
where
![]() . (A.44)
. (A.44)
Using replacement![]() ,
, ![]() ,
, ![]() into RHS of the Equation (A.44) one obtain
into RHS of the Equation (A.44) one obtain
![]()
(A.45)
![]() ,
, ![]() ,
, ![]() , see Equation (3.1) and
, see Equation (3.1) and
![]() , (A.46)
, (A.46)
![]() . (A.47)
. (A.47)
![]() . (A.48)
. (A.48)
From (A.43)-(A.48) one obtain
![]() . (A.49)
. (A.49)
Let us to choose an sequence ![]() such that
such that
1) ![]() and
and
2)![]() .
.
We note that from 2) follows that: perturbative expansion
![]() ,
,
Vanishes in the limit![]() . From (A.49) one obtain
. From (A.49) one obtain
![]() . (A.50)
. (A.50)
Let us to choose now an subsequence ![]() such that the limit:
such that the limit: ![]()
exist and ![]() (A.51)
(A.51)
From (A.51) and Proposition A.1 one obtain
![]() . (A.52)
. (A.52)
From (A.50), (A.51) and (A.52) one obtain
![]()
Proof of the statements (3)-(6) is similarly to the proof of the statements (1)-(2).
Theorem A.1. Let![]() ,
, ![]() ,
,
where ![]() is given via Equations (A.22a)-(A.22b). Then
is given via Equations (A.22a)-(A.22b). Then
![]() (A.53.a)
(A.53.a)
![]() (A.53.b)
(A.53.b)
Here
![]() , (A.54)
, (A.54)
![]() . (A.55)
. (A.55)
Proof. We remain that
![]() . (A.56)
. (A.56)
From Equation (A.56) we obtain
![]() . (A.57)
. (A.57)
Let us to choose now an sequences![]() ,
, ![]() ,
, ![]() such that:
such that:
1)![]() ,
,
2)![]() , (A.58)
, (A.58)
3)![]() (A.59)
(A.59)
Therefore from inequality (A.57), Equation (A.58) and inequality (A.59) we obtain
![]() (A.60)
(A.60)