1. Introduction
This paper continues an effort to model life based upon the first principles, with emphasis to capture the mind creativity mystery. The effort is based upon a hypothetical particle of life introduced in [1] , in which a possible extension of modern physics to include physics of Life is discussed. In this work, it has been proven that there exists a fundamentally new type of dynamical systems (represented by L-particles) that can evolve from disorder to order without external forces thereby violating the second law of thermodynamics. It has been demonstrated that these systems belong neither to Newtonian, nor to quantum physics. Their departure from Newtonian me- chanics is due to a feedback from the underlying Liouville equation to the equations of motion that represents an additional (internal) information force. Topologically this feedback shifts L-particles towards quantum mechan- ics. However since the information force is different from the quantum potential, the L-particles are not quantum, and they can be identified as quantum-classical hybrids. Therefore L-particles dwell in an abstract mathematical world rather than in the physical world, as we know it. This means that behavior of L-particles can be computed, but not simulated. This also means that L-particles, in principle, cannot be composed out of physical particles, [1] . The topology of L-particle is demonstrated in Figure 1.
This paper proposes a mathematical formalism for describing the machinery of human mind creativity based upon the hypothetical model of particle of life. A mind is understood as the set of cognitive faculties that enables consciousness, perception, thinking, judgment, and memory―a characteristic of humans. Adopting terminology of computer science, we will associate brain with a computer, and mind―with a set of algorithms implemented by this computer. This allows us to distance ourselves from biological aspects of brain and concentrate on in- trinsic mathematical properties of mind. Similar abstraction―ignorance of metabolism and reproduction―made the particle of life an isolated system. Since some functions of mind support discreteness of cognition, but others support its continuity, while time in physics is always continuous, an attempt to overcome the continuous/dis- crete duality of mind performance is implemented via utilization of special critical points: terminal attractors and repellers, [2] , that act as autonomous biological clock. In this paper, attention is concentrated upon the discrete mode of the mind activity that is based upon the continuous mode mentioned above and represents an extension of this mode. Actually the discrete model should be considered as the next step in study of mind dynamics since it provides a bridge to mathematical origin of self-generated novelties in such brunches as mathematical logic and linguistic, i.e. the highest level activities of human mind. A human intelligence has always been a mystery for physicists, and an obstacle for artificial intelligence. It was well understood that human behavior, and in par- ticular, the decision making process, is governed by feedbacks from the external world, and this part of the problem was successfully simulated in the most sophisticated way by control systems. However, in addition to that, when the external world does not provide sufficient information, a human turns for an “advice” to his expe- rience, and that is associated with a common sense. In this paper, the common sense is captured via spontaneous emergence of new information generated by human mind without external interaction.
It should be emphasized that the proposed model of mind as a part of the hypothetical particle of life is based only upon one assumption: The ability to move from disorder to order without external sources, i.e. in violation of the second law of thermodynamics. Starting with that postulate, mathematical formalism takes over and leads to a quantum-inspired model of mind.
2. Hypothetical Particle of Life
In this section, we briefly discuss a hypothetical model of L-particle introduced in [1] . The model is based upon departure from Newtonian dynamics as a result of a feedback from the Liouville equation to the equation of mo- tion (Figure 1).
We will start with derivation of a one-dimensional case that illuminates departure from Newtonian dynamics. For mathematical clarity, we will consider here a motion of a unit mass under action of a force f depending upon the velocity v and time t and present it in a dimensionless form
(1)
referring all the variables to their representative values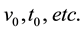 
![]()
Figure 1. Classic physics, quantum physics and physics of life.
If initial conditions are not deterministic, and their probability density is given in the form
(2)
while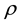 
is a single-valued function, then the evolution of this density is expressed by the corresponding Liou- ville equation
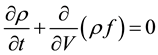(3)
The solution of this equation subject to initial conditions and normalization constraints (2) determines proba- bility density as a function of V and t:
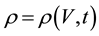(4)
Remark. Here and below we make distinction between the random variable v(t) and its values V in probability space.
In order to deal with the constraint (2), let us integrate Equation (3) over the whole space assuming that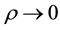 
at 
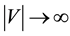and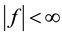
. Then
(5)
Hence, the constraint (2) is satisfied for 
if it is satisfied for 
Let us now specify the force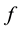 
as a feedback from the Liouville equation
(6)
and analyze the motion after substituting the force (6) into Equation (2)
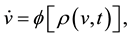(7)
This is a fundamental step in our approach. Although the theory of ODE does not impose any restrictions upon the force as a function of space coordinates, the Newtonian physics does: equations of motion are never coupled with the corresponding Liouville equation. Nevertheless such a Liouville feedback does not lead to any physical inconsistence.
Substituting the force ![]()
from Equation (6) into Equation (3), one arrives at the nonlinear equation of evo- lution of the probability density
![]()
(8)
In order to illustrate mathematical aspects of the concepts of Liouville feedback in systems under considera- tion as well as associated with its instability and randomness, let us take the feedback (3) in the form
![]()
(9)
and therefore, Equations (7) and (8) form the following system
![]()
(10)
![]()
(11)
We will start analysis of this system with the simple case when
![]()
(12)
to obtain the following equation of motion
![]()
(13)
This equation should be complemented by the corresponding Liouville equation (in this particular case, the Liouville equation takes the form of the Fokker-Planck equation)
![]()
(14)
Here v stands for a particle velocity, and ![]()
is the diffusion coefficient.
Since
![]()
(15)
the solution of Equation (14) subject to the sharp initial condition
![]()
(16)
describes diffusion of the probability density.
Substituting this solution into Equation (13) at V = v, one arrives at the differential equation with respect to v(t)
![]()
(17)
and therefore,
![]()
(18)
where C is an arbitrary constant. Since v = 0 at t = 0 for any value of C, the solution (18) is consistent with the sharp initial condition for the solution (16) of the corresponding Liouvile Equation (14). The solution (18) de- scribes the simplest irreversible motion: it is characterized by the “beginning of time” where all the trajectories intersect (that results follows from the violation of Lipchitz condition at t = 0, Figure 2), while the backward motion obtained by replacement of t with (?t) leads to imaginary values of velocities. One can notice that the probability density (18) possesses the same properties.
It is easily verifiable that the solution (18) has the same structure as the solution of the Madelung equation [1] , although the dynamical system (13), (14) is not quantum! The explanation of such a “coincidence” is very sim- ple: the system (13), (14) has the same dynamical topology as that of the Madelung equation where the equation of conservation of the probability is coupled with the equation of conservation of the momentum (see Figure 1). As will be shown below, the system (13), (14) neither quantum nor Newtonian, and we will call such systems quantum-inspired, or self-supervised.
Further analysis of the solution (18) demonstrates that this solution is unstable since
![]()
(19)
and therefore, an initial error always grows generating randomness. Initially, at t = 0, this growth is of infinite rate since the Lipchitz condition at this point is violated
![]()
Figure 2. Stochastic process and probability density.
![]()
(20)
This type of instability has been introduced and analyzed in [3] . The unstable equilibrium point ![]()
has been called a terminal repeller, and the instability triggered by the violation of the Lipchitz condition― non-Lip- chitz, or terminal instability. The basic property of the non-Lipchitz instability is the following: if the initial con- dition is infinitely close to the repeller, the transient solution will escape the repeller during a bounded time while for a regular repeller the time would be unbounded. Indeed, an escape from the simplest regular repeller can be described by the exponent![]()
. Obviously ![]()
if![]()
, unless the time period is unbounded. On the contrary, the period of escape from the terminal repeller (18) is bounded (and even infinitesimal) if the initial condition is infinitely small (see Equation (20)).
Considering first Equation (18) at fixed C as a sample of the underlying stochastic process (16), and then va- rying C, one arrives at the whole ensemble characterizing that process (see Figure 2). The curves that envelope the cross-sectional blue areas at ![]()
present the probability density distribution at constant times. One can verify that, as follows from Equation (16) [4] , the expectation and the variance of this process are, respec- tively
![]()
(21)
The same results follow from the ensemble (18) at![]()
. Indeed, the first equality in (21) results from symmetry of the ensemble with respect to v = 0. The second one follows from the fact that
![]()
(22)
It is interesting to notice that the stochastic process (16) is an alternative to the following Langevin equation, [5]
![]()
(23)
that corresponds to the same Fokker-Planck Equation (14). Here ![]()
is the Langevin (random) force with zero mean and constant variance![]()
.
Thus, the emergence of self-generated stochasticity is the first basic non-Newtonian property of the dynamics with the Liouville feedback.
We will continue with another extreme case of the feedback (9) assuming that
![]()
(24)
obtaining
![]()
(25)
and therefore, the equation of motion and the Liouville equation are
![]()
(26)
![]()
(27)
The solution of Equation (27) subject to the initial conditions ![]()
and the normalization constraint (2) is given in the following implicit form [6] ,
![]()
(28)
This solution subject to the initial conditions and the normalization constraint, describes propagation of initial distribution of the density ![]()
with the speed V that is proportional to the values of this density, i.e. the higher values of ![]()
propagate faster than lower ones. As a result, any compressive part of the wave, where the propagation velocity is a decreasing function of V, ultimately “breaks” to give a triple-valued (but still conti- nuous) solution for![]()
. Eventually, this process leads to the formation of strong discontinuities that are re- lated to propagating jumps of the probability density. In the theory of nonlinear waves, this phenomenon is known as the formation of a shock wave (Figure 3). Thus, as follows from the solution (28), a single-valued continuous probability density spontaneously transforms into a triple-valued, and then, into discontinuous dis- tribution.
![]()
Figure 3. Formation of shock wave in probability space.
In aerodynamical application of Equation (27), when ![]()
stands for the gas density, these phenomena are eliminated through the model correction: at the small neighborhood of shocks, the gas viscosity ![]()
cannot be ignored, and the model must include the term describing dissipation of mechanical energy. The corrected model is represented by the Burgers’ equation
![]()
(29)
As shown in [6] , this equation has continuous single-valued solution (no matter how small is the viscosity![]()
), and that provides a perfect explanation of abnormal behavior of the solution of Equation (27). Similar correction can be applied to the case when ![]()
stands for the probability density if one includes Langevin forces ![]()
into Equation (26)
![]()
(30)
Then the corresponding Fokker-Planck equation takes the form (29). It is reasonable to assume that small random forces of strength ![]()
are always present, and that protects the mathematical model (26), (27) from singularities and multi-valuedness in the same way as it does in the case of aerodynamics.
t is interesting to notice that Equation (29) can be obtained from Equation (26) in which random force is re- placed by an additional Liouville feedback
![]()
(31)
and that is exactly Equation (11).
Equation (29) is known as the Burgers equation, and it has the exact analytical solution [6]
![]()
(32)
where
![]()
Although this solution is well known, it should be emphasized that in our case it occurs in the probability space. This means that if one runs Equation (31) independently many times starting with different initial condi- tions and compute the statistical characteristics of the family of these solutions, he will arrive at the evolution of the probability density described by Equation (33).
As a particular case of the solution (32), consider a long-term behavior of an initial step
![]()
that diffuses into the steady profile [1] :
![]()
(33)
moving with the constant speed
![]()
when v/t is fixed, and![]()
.
In this case, Equation (33) describes a stationary stochastic process to be applied to the proposed model of mind.
One can verify that the additional (normalization) constraint imposed upon the probability density that is a state variable of the Burgers Equation (29) is satisfied
![]()
(34)
Indeed, as follows from (34), if the normalization constraint is satisfied at the initial condition, it will be satis- fies for all times.
An important non-classical property of the solution of this equation is a decrease of entropy. Indeed,
![]()
(35)
Obviously, presence of small diffusion, when![]()
, does not change the inequality (35) during certain pe- riod of time (However, eventually, for large times, diffusion takes over, and the inequality (3) is reversed).
The inequality (35) is of fundamental importance: it confirms existence of such an isolated dynamical system that violates the second law of thermodynamics by decreasing the entropy during some period of time while ob- eying the rules of mathematics. Therefore if the corresponding hypothetical particle exists, it cannot belong to the modern physics, as we know it; actually it should belong to an extended physical world in the form of a quantum-classical hybrid. However, the assumption about existence of such a particle is justified by similarity between its dynamical properties and those of living systems. The analysis of these similarities is performed in [1] , and we present a brief conclusive remark below.
The proposed model illuminates the “border line” between living and non-living systems. The model intro- duces a biological particle that, in addition to Newtonian properties, possesses the ability to process information. The probability density can be associated with the self-image of the biological particle as a member of the class to which this particle belongs, while its ability to convert the density into the information force―with the self-awareness (both these concepts are adopted from psychology). Continuing this line of associations, the equ- ation of motion, Equation (10) can be identified with a motor dynamics, while the evolution of density (see Eq- uation (11))―with a mental dynamics. Actually the mental dynamics play the role of the Maxwell sorting de- mon: it rearranges the probability distribution by creating the information potential and converting it into a force that is applied to the particle. One should notice that mental dynamics describes evolution of the whole class of state variables (differed from each other only by initial conditions), and that can be associated with the ability to generalize that is a privilege of living systems. Continuing our biologically inspired interpretation, it should be recalled that the second law of thermodynamics states that the entropy of an isolated system can only increase. This law has a clear probabilistic interpretation: increase of entropy corresponds to the passage of the system from less probable to more probable states, while the highest probability of the most disordered state (that is the state with the highest entropy) follows from a simple combinatorial analysis. However, this statement is correct only if there is no Maxwell’s sorting demon, i.e., nobody inside the system is rearranging the probability distri- butions. But this is precisely what the Liouville feedback is doing: it takes the probability density ![]()
from Eq- uation (11), creates functionals and functions of this density, converts them into a force and applies this force to the equation of motion (10). As already mentioned above, because of that property of the model, the evolution of the probability density becomes nonlinear, and the entropy may decrease “against the second law of thermody- namics”. Obviously the last statement should not be taken literary; indeed, the proposed model captures only those aspects of the living systems that are associated with their behavior, and in particular, with their motor- mental dynamics, since other properties are beyond the dynamical formalism. Therefore, such physiological processes that are needed for the metabolism are not included into the model. That is why this model is in a formal disagreement with the second law of thermodynamics while the living systems are not. In order to further illustrate the connection between the life-nonlife discrimination and the second law of thermodynamics, consid- er a small physical particle in a state of random migration due to thermal energy, and compare its diffusion, i.e. physical random walk, with a biological random walk performed by a bacterium. The fundamental difference between these two types of motions (that may be indistinguishable in physical space) can be detected in proba- bility space: the probability density evolution of the physical particle is always linear and it has only one attrac- tor: a stationary stochastic process where the motion is trapped. On the contrary, a typical probability density evolution of a biological particle is nonlinear: it can have many different attractors, but eventually each attractor can be departed from without any “help” from outside.
The proposed model can be interpreted as representing interactions of the agent with the self-image and the images of other agents via the mechanisms of self-awareness. In order to associate these basic concepts of psy- chology with our mathematical formalism, we have to recall that living systems can be studied in many different spaces such as physical (or geographical) space as well as abstract (or conceptual) spaces. The latter category includes, for instance, social class space, sociometric space, social distance space, semantic space etc. Turning to our model, one can identify two spaces: the physical space x, t in which the agent state variables ![]()
evolve, (see Equation (10)), and an abstract space in which the probability density of the agent’s state variables evolve (see Equation (11)).The connection between these spaces have been already described earlier: if Equation (10) is run many times starting with the same initial conditions, one will arrive at an ensemble of different random so- lutions, while Equation (11) will show what is the probability for each of these solutions to appear. Thus, Equa- tion (11) describes the general picture of evolution of the communicating agents that does not depend upon par- ticular initial conditions. Therefore, the solution of this equation can be interpreted as the evolution of the self- and non-self images of the agents that jointly constitutes the collective mind in the probability space. Based upon that, one can propose the following interpretation of the model of communicating agents: considering the agents as intelligent subjects, one can identify Equation (10) as a model simulating their motor dynamics, i.e. actual motions in physical space, while Equation (11) as the collective mind composed of mental dynamics of the agents. Such an interpretation is evoked by the concept of reflection in psychology. Reflection is traditionally understood as the human ability to take the position of an observer in relation to one’s own thoughts. In other words, the reflection is the self-awareness via the interaction with the image of the self. Hence, in terms of the phenomenological formalism proposed above, a non-living system may possess the self-image, but it is not equipped with the self-awareness, and therefore, this self-image is not in use. On the contrary, in living systems the self-awareness is represented by the information forces that send information from the self-image (11) to the motor dynamics (10). Due to this property that is well-pronounced in the proposed model, an intelligent agent can run its mental dynamics ahead of real time, (since the mental dynamics is fully deterministic, and it does not depend explicitly upon the motor dynamics) and thereby, it can predict future expected values of its state va- riables; then, by interacting with the self-image via the information forces, it can change the expectations if they are not consistent with the objective. Such a self-supervised dynamics provides a major advantage for the cor- responding intelligent agents, and especially, for biological species: due to the ability to predict future, they are better equipped for dealing with uncertainties, and that improves their survivability. It should be emphasized that the proposed model, strictly speaking, does not discriminate living systems of different kind in a sense that all of them are characterized by a self-awareness-based feedback from mental (11) to motor (10) dynamics. However, in primitive living systems (such as bacteria or viruses) the self-awareness is reduced to the simplest form that is the self-nonself discrimination; in other words, the difference between the living systems is represented by the level of complexity of that feedback.
3. Terminal Singularities in Discrete Events Models
Since we are planning to concentrate upon discrete aspect of cognitive performance of mind, the most transpa- rent mathematical tool for that are time-delay equations. However, the problem with these equations is in their nonlocality. Indeed because the known laws of physics are all local, and because nonlocal interactions combined with relativity lead to causal paradoxes, many physicists find nonlocal models unacceptable. On the first sight, in our case this argument can be dismissed on the ground that the model of particle of life (that is planned to be the base of the model of mind) is quantum-inspired and it manifests entanglement that is a fundamentally non- local effect [1] [6] . However, the entanglement-based nonlocalities are not related to time-space nonlocalities of time-delay equations, and therefore, this counter-argument should be disqualified. In order to replace the time- delay equations with differential equations, we apply terminal singularities [2] , represented by terminal attractor and terminal repellers. A brief description of this concept is presented below.
The governing equations of classical dynamics are based upon Newton’s laws
![]()
(36)
where L is the Lagrangian and q and ![]()
are the generalized coordinates and velocities, include a dissipation function ![]()
that is associated with the friction forces
![]()
(37)
The structure of the function (37) does not prescribed by the Newton’s laws, and, strictly speaking, some ad- ditional assumptions should be made in order to define them. The natural assumption (that has never been chal- lenged) is that these functions can be expanded in the Taylor series with respect to an equilibrium state
![]()
(38)
Obviously this requires the existence of the derivatives
![]()
(39)
i.e., Fi must satisfy the Lipchitz condition. This condition allows one to describe the Newtonian dynamics within the mathematical framework of classical theory of differential equation. However, there is a certain price for such mathematical “convenience”: The Newtonian dynamics with dissipative forces remain fully reversible in the sense that its governing equations are invariant with respect to time inversion![]()
. In this view, future and past play the same role: nothing can appear in future that could not have already existed in the past, since the trajectories followed by the particles can never cross in finite time. This means that classical dynamics can- not explain the emergence of new dynamical patterns in nature in which non-equilibrium dynamics does.
In order to trivialize the mathematical part of our argument, let us consider the one-dimensional motion of a particle decelerated by a friction force
![]()
(40)
in which m is mass and w is velocity. Invoking the assumption (39) one can linearize the force F with respect to the equilibrium v = 0:
![]()
(41)
and the solution of Equation (40) for ![]()
is
![]()
(42)
As follows from Equation (42), the equilibrium w = 0 cannot be approached in finite time. A usual explana- tion of this paradox is that to accuracy of our limited scale of observation, the particle “actually” approaches the equilibrium in finite time. In other words, eventually the trajectories (42) and w = 0 become so close that we cannot distinguish them. The same type of explanation is used for emergence of chaos: if two trajectories origi- nally are “very close” and then they diverge exponentially, the same initial conditions can be applied to either of them, and therefore, the motion cannot be traced.
Turning to the example (40), let us assume that
![]()
(43)
in which N is an odd number.
By selecting a large N, one can make k close to 1, so that Equations (41) and (43) will be almost identical every- where excluding a small neighborhood of the equilibrium point w = 0 , while, as follows from Equation (43), at this point
![]()
(44)
Hence the condition (39) is violated; the friction force grows sharply at the equilibrium point, and then it gradually approaches the straight line (41). This effect can be interpreted as a jump from static to kinetic friction. It appears that this small difference between the friction forces (41) and (43) leads to fundamental change in Newtonian dynamics: the time of approaching the equilibrium w = 0 becomes finite. Indeed, as follows from (40) and (43)
![]()
(45)
Obviously this integral diverge in the classical case when![]()
.
As shown in [2] , the equilibrium point v = 0 of Equation (43) represents a terminal attractor that is “infinitely” stable and is intersected by all the attracted transients.
Therefore the uniqueness of the solution at w = 0 is violated, and the motion for t < t1 or t < t2 is totally for- gotten. This is a mathematical implication of irreversibility in dynamics (43).
So far we were concerned with the stabilizing effects of dissipative forces. However, as is well known from dynamics of non-conservative systems, these forces can destabilize the motion when they feed external energy into the system (the transmission of energy from laminar to turbulent flow in fluid dynamics, or from rotation to oscillations in dynamics of flexible systems). In order to capture the fundamental properties of these effects in the case of non-Lipchitz, or “terminal” dissipative forces (43) by using the simplest mathematical model, let us turn to Equation (43) and assume that now the friction force feeds energy into the system
![]()
(46)
One can verify that that for Equation (46), the equilibrium point w = 0 becomes a terminal repeller, and since
![]()
(47)
it is infinitely unstable. If the initial condition is infinitely close to this repeller, the transient solution will escape it during a finite time period
![]()
(48)
while for a regular repeller the time period would be infinite. But in addition to that, terminal repellers possess even more surprising characteristics: the solution of Equation (46) becomes totally unpredictable.
![]()
(49)
Indeed, two different motions described by Equation (49) are possible for “almost the same” initial conditions
![]()
(50)
The most essential property of this result in that the divergence of these two solutions is characterized by an unbounded rate
![]()
(51)
In contrast to the classical case where![]()
, here ![]()
can be defined within an arbitrarily small time in- terval t0 since during this interval the initial infinitesimal distance between the solutions becomes finite. Thus a terminal repeller represents a vanishingly small, but infinitely powerful “pulse of unpredictability” that is pump- ed into the system via terminal dissipative forces. Obviously, failure of the uniqueness of the solution here re- sults from the violation of the Lipchitz condition (39) at w = 0.
As known in theory of chaos and turbulence, a combination of stabilizing and destabilizing effects can lead to a new phenomenon: intermittency. In order to describe similar effects in dynamics with terminal dissipating forces, let us slightly modify Equation (46)
![]()
(52)
Here stabilization and destabilization effects alternate. With the initial conditions
![]()
(53)
the exact solution of Equation (52) consists of a regular solution
![]()
(54)
and a singular solution
![]()
(55)
During the first period ![]()
the equilibrium point (55) is a terminal repeller. Therefore within this period the motion can follow one of two possible trajectories (54), each with the probability 1/2. These trajecto- ries diverge with unbounded rate (51) at w = 0. During the next period, ![]()
, the equilibrium point (55) becomes the terminal attractor: the solution approaches it at![]()
, and it remains at rest until![]()
. After that the terminal attractor becomes a terminal repeller, and the solution escapes again, etc., Figure 4.
It is important to notice that each time the system escapes the terminal repeller, the solution splits into two symmetric branches, so that there are 2n possible scenarios of the oscillations with respect to the center w = 0, while each scenario has the probability 2−n to occur, where n is the number of cycles. Hence the motion (54) re- sembles chaotic oscillations known from classical dynamics: it combines random characteristics with the attrac- tion to the center. However in classical case, chaos is caused by a supersensitivity to the initial conditions, while the uniqueness of the solution for the unique initial conditions is guaranteed. In contrast to that, the chaos in the oscillations (54) is caused by the failure of the uniqueness of the solutions at the equilibrium points, and it has a
![]()
Figure 4. Terminal chaotic oscillations.
well-organized probabilistic structure. Since the time of approaching the equilibrium point w = 0 by the solution (54) is finite, this type of chaos can be called terminal.
4. Terminal Model of Punctuated Evolution
4.1. Governing Equations
The model proposed in this section is based upon dynamical simulation of terminal oscillations introduced above. We start with a rectilinear motion of a particle of unit mass (m = 1) described by the following differen- tial equations:
![]()
(56)
![]()
(57)
where x and w are the position and velocity, respectively, and ![]()
is infinitesimal ambient noise that triggers the mechanism of instability of terminal repellers.
Let us start with Equation (56). Actually this is a particular case of Equation (52) at k = 1/3. The solution of this equation subject to the initial conditions (53) is
![]()
(58)
and a singular solution
![]()
(59)
These two solutions coexist at t = 0, and that is possible because at this point the Lipchitz condition fails
![]()
(60)
As shown in Figure 4, the particle velocity w performs oscillations with respect to its zero value in such a way that the positive and negative branches of the solution (58) alternate randomly after each period equal to![]()
.
It should be emphasized again that the noise ![]()
is not driving the solution of Equation (56): it only controls the energy supply via the harmonic oscillations![]()
. As follows from Equation (56), ![]()
can be ignored when ![]()
or when![]()
, but the solution is stable, i.e. at ![]()
however, it becomes significant during the instants of instability, i.e. at ![]()
Turning to Equation (57), one obtains the distance between two adjacent equilibrium positions of the particle
![]()
(61)
where ![]()
is the gamma-function.
Thus the equilibrium positions of the particle are
![]()
(62)
while the positive and negative signs randomly alternate with the probability p, where p is the probability that![]()
. The equilibrium positions are stable when![]()
, and unstable when![]()
. Since the Lipchitz condition at these equilibrium points is violated, that makes them terminal attractors and terminal repellers, re- spectively. As a result of that, the transition time ![]()
from one point to another is finite.
Thus, the solution of Equations (56) and (57) combines acting (the transition from one equilibrium point to another), and “thinking” (the decision making process based upon![]()
).
4.2. Dynamics of Probabilities
Since the solutions of Equations (56) and (57) include random components, it is useful to describe them in terms of probabilities. For that purpose, let us introduce a function![]()
, which represents the probability that the particle occupies the equilibrium position x at time![]()
. Then, based upon the property of the solution solution (62), one can write the following partial difference equation as a random walk [7]
![]()
(63)
![]()
(64)
supplemented by the normalization constraint
![]()
(65)
In case of unrestricted random walk, ![]()
in Equation (65).
Equation (63) can be considered as a terminal version of the Liouville equation generated by the system (56), (57). Indeed, as the classical Liouville equation (see Equation (3)), it describes evolution of an initial error dis- tribution. However, in terminal version of dynamics, this error occurs only in discrete points representing ter- minal repellers, and that makes the Liouville equation discrete as well.
One can notice that in the limit case ![]()
Equation (63) tends to the Fokker-Planck equation (see Equation (14)).
4.3. The Noise Structure
In this sub-section we will analyze possible structures of the noise that is responsible for triggering the transition from one equilibrium to another in the direction depending upon![]()
.
Regardless of the type of the corresponding terminal repeller, the noise can be derived from a sample of an underlying stationary stochastic process characterized by some probability density![]()
. Suppose that
![]()
(66)
where ![]()
is the mean of ![]()
![]()
(67)
and ![]()
is some deterministic variable to be defined below.
Then
![]()
(68)
while
![]()
(69)
Obviously any stationary stochastic process uniquely defines the function![]()
.
In general, ![]()
can depend upon the particle velocity w, particle coordinate x, its probability distribution f(x), and the functionals of f(x) such as the mean
![]()
(70)
the variance
![]()
(71)
or the Shannon uncertainty (entropy)
![]()
(72)
i.e.
![]()
(73)
Actually, all the variety and complexity of the particle behavior described by Equations (56) and (57) is de- fined by the structure of the function (73). A variety of structures of this function as well as specific characteris- tics of the corresponding behaviors was analyzed in [3] . In the next section we will concentrate upon the case
![]()
(74)
with application of the terminal model of punctuated evolution to Boolean dynamics.
5. Terminal Model of Boolean dynamics
In this section, we start with a critical review of the dynamics of a set of n variables ![]()
that have two possible values (say 0 and 1, or −1, and 1) [4] [8] . These variables interact with each other according to some given rules, specified through a set of Boolean coupling functions that determine the variables at the next time-step, and thereby generate the dynamics of the system. Such a discrete stepping of a set of Boolean va- riables, also known in general terms as a Boolean network, is of potential interest in several different fields, ranging from gene regulation and control, to modeling democracy and social organization. In the context of this paper, Boolean nets could be considered as a candidate of a model of mind.
Any model of a Boolean net starts from n binary elements
![]()
(75)
In the time stepping, each of these Boolean elements is defined by a function of all the elements (75), or at least, some of them. More precisely, the value of ![]()
at time t + 1 is determined by the value of its Ki control- ling elements at time t, while![]()
.
A typical Boolean network consists of a set of n nodes, and each of these nodes receives inputs from K other nodes. For K = n, the dynamics can be presented in the following form
![]()
(76)
where the synapse weights ![]()
and the activation threshold ![]()
are random variables that can be adapted (in learning processes) or stay fixed (in recall or association processes). Note that with the above definitions, the nodes have the values (75).
In [9] , K. Kurten has considered the case in which the synapse weights are independent random variables dis- tributed according to a symmetric probability function![]()
. By analyzing the Hamming distance, he has shown that this kind of network has three phases (frozen, critical and chaotic) depending on the connectivity and the dilution of the network (dilution is a measure of the amount of nodes for which the synapse weight is 0). The main result is that for low connectivity and dilution, the model (76) exhibits exactly the same dynamics in the Hamming distance [9] , as neural networks in physical space [10] .
The interest to Boolean dynamics as a candidate for the model of mind is due to its capability to process dis- crete-events with application to logic and linguistic that is the fundamental privilege of human mind. However, the existing models of Boolean dynamics described above have two limitations that disqualify them from that purpose.
The first limitation is their non-locality since they are presented by difference rather than differential equa- tions. However as mentioned in Section 3, since the known laws of physics are all local, and because nonlocal interactions combined with relativity lead to causal paradoxes, many physicists find nonlocal models unacceptable.
The second limitation is that these models are not isolated systems. As emphasized in the Introduction, the proposed model of mind as a part of the hypothetical particle of life is based only upon one assumption: the abil- ity to move from disorder to order without external sources, i.e. in violation of the second law of thermodynam- ics. Starting with that postulate, mathematical formalism is supposed to take over and to lead to a quantum-in- spired model of mind.
In order to remove these limitations, we apply the terminal model of punctuated evolution presented in the previous section. We will concentrate upon the case of Equation (73) when
![]()
(77)
and consider the equation
![]()
(78)
subject to the initial conditions
![]()
(79)
The solution consists of a regular solution
![]()
(80)
and a singular solution
![]()
(81)
These two solutions coexist at t = 0, and that is possible because at this point the Lipchitz condition fails
![]()
(82)
During the first period![]()
, the equilibrium point (81) is a terminal repeller. Therefore within this period, the motion can follow one of two possible trajectories (80), each with the probability 1/2. These trajecto- ries diverge with unbounded rate (51) at w = 0. During the next period, ![]()
, the equilibrium point (81) becomes the terminal attractor: the solution approaches it at![]()
, and it remains at rest until![]()
. After that the terminal attractor becomes a terminal repeller, and the solution escapes again, but be- cause of the additional term in Equation (78), it has only one trajectory for the escape. Indeed, let us turn to Fig- ure 4: if initially the particle moves right, (see the green trajectory), then after the period of rest, it will move back, (see the red trajectory); inversely, if initially it moves left, (see the red trajectory), then after the period of rest, it will move back on the green trajectory. Therefore the particle (see Equation (57)) in both cases will return to the original position (81) after one step aside, i.e. instead of unrestricted random walk considered above, it performs a restriction random walk, i.e. random oscillations with respect to the origin
![]()
(83)
with an unstable transitional point
![]()
(84)
Let us concentrate on the variable w. Turning to Equation (80) and selecting the constants ![]()
and ![]()
such that
![]()
(85)
one arrives at a Boolean variable (75). Unlike a “classical” Boolean variable that takes values 0 and 1, this vari- able takes values (−1) and 1, while zero plays the role of a transitional point that, as a result of its instability, provides a passage to the stable points (−1) or 1. This transitional point plays another important role: it separates future from past in such a way that at this point, past is completely forgotten, and the motion starts afresh. The last property is a fundamental characteristic of terminal attractors/repellers.
Figure 5 illustrates dynamics of probability of the binary evolution described by Equation (78). Let us assume that the particle is located at the point w = 0 at t = 0. As long as this point is a terminal attractor, the probability is equal to 1. When this point becomes a terminal repeller, the probability splits in two equal parts, and the par- ticle can go right or left with the probability 1/2. It will stay there until this new point becomes a terminal repel- ler, and it moves back to the zero point that is becoming a terminal attractor. This pattern continues indefinitely.
Applying the formula for the binary entropy function
![]()
(86)
where
![]()
(87)
one calculates the change of the entropy: it starts with zero value at t = 0
![]()
(88)
Then it jumps to its maximum value at ![]()
![]()
(89)
Finally it returns to its initial value (88) at ![]()
(see Figure 6).
On the first sight, it seems surprising that entropy may decrease (see the green line). However, turning to the governing Equation (78), one concludes that such an “inverse” evolution results from the fact that this system is not isolated, although it is closed, (there is no mass exchange). Indeed, it consumes energy via the harmonic os- cillations![]()
, and therefore, the green line in Figure 6 does not violate the second law of thermodynamics.
Prior to generalizing Equation (78) to the n-dimensional case, we will emphasize the role of the term (77). When![]()
, Equation (78) can be simplified to the following
![]()
(90)
and the term (77) provide stability of Equation (90). As a result of that, the particle returns to its initial position w = 0 thereby performing restricted one-step random walk. Obviously without this term, the random walk would be unrestricted, and the variable w would not be a Boolean one.
In order to introduce not only the Boolean variables, but the Boolean functions as well, we will recall that
![]()
(91)
Therefore Equation (90) can be approximated as
![]()
Figure 5. Probability of terminal version of Boolean dynamics.
![]()
Figure 6. Change of binary entropy function.
![]()
(92)
Let us now move to the n-dimensional case
![]()
(93)
where the synapse weights ![]()
are constants.
However, in order to prevent the system (93) from an unrestricted walk, the synapse weights should be chosen such that that the system
![]()
(94)
is asymptotically stable. The sufficient conditions for that are the following
![]()
(95)
i.e. ![]()
is symmetric positive-definite matrix. The properties (95) provide the asymptotic stability of the sys- tem (95) as well as the asymptotic stability at ![]()
of the original system (93) when![]()
.
Let us turn to the analysis of the system (93). Comparing this system with the one-dimensional case (78), one notice that each Boolean variable wi is not affected by the rest of the variables, and the role of the Boolean func- tions
![]()
(96)
is to provide the stability of the system (93) at ![]()
when![]()
. Therefore the probability dynamics of each Boolean variable is described in Figure 5, and the dynamics of the binary entropy function is illustrated in Figure 6. As follows from Equation (96), the values of the Boolean functions Bi are changed with changes of the corresponding Boolean variables.
6. Proposed Model of Human Mind
In this section, we discuss the system (93) as a candidate for the model of the human mind. Unlike the Boolean dynamics model (76) that is nonlocal, the model (93) is described by the system of differential (but not differ- ence!) equations, and therefore, it is local. Hence the first limitation of the model (76) formulated in the previous Section is removed in the system (93). However the second limitation is still there: the system (93), as well as the system (76), is not isolated. Indeed the system (93) consumes energy via the harmonic oscillations![]()
. In addition to that, it requires some energy to support a stationary stochastic process ![]()
for generating infi- nitesimal noise (see Equations (66) and (67)). It should be reminded that the main challenge of this work is to propose a model of mind based only upon one assumption: the ability to move from disorder to order without external sources, i.e. in violation of the second law of thermodynamics. Starting with that postulate, mathemati- cal formalism is supposed to take over and lead to a model of mind.
In order to achieve that, we combine the model of mind with the corresponding model of the particle of life (L-particle) allowing the mind to “borrow” energy from the L-particle. Such a symbiosis is natural from the physiological viewpoint. Thereby we introduce a master-slave system that is isolated from the external world. Such an idealization allows us to capture distinguished properties of livings that possess intelligence.
Let us turn to the system (13), (14) which describes the dynamics of L-particle. From its solution given by Equation (18), one can express
![]()
(97)
Turning to the stationary stochastic process generated by L-particle and described by Equation (33), one can adapt from it random values of noise (66)
![]()
(98)
In order to obtain random samples ![]()
of the variable v distributed with the density (33), one should run si- multaneously many identical L-particles with the same initial conditions. As shown in [1] , each particle will have different values of the constants![]()
, with the samples velocities ![]()
to be distributed with the density (33).
Now with help of Equations (97) and (98), the system (93) can be presented in the following form
![]()
(99)
The system is still not closed because of additional variables v and![]()
. For the closure this system is supposed to be considered together with equations of L-particle
![]()
(100)
![]()
(101)
Now the system (99), (100) and (101) is closed and isolated. Because of the master-slave coupling we can as- sume that the functions (97) and (98) are preset, and analyze Equations (99) separately from Equations (100) and (101).
As follows from Equation (97), the system (99) was set up based upon preserving the time scale of the L-par- ticle. However, in general, the mind may have its intrinsic time scale. Indeed, substituting ![]()
instead of t we change the scale of time: it runs infinitely faster (almost by a jump) in the very beginning and then it slows down approaching zero at infinity. The role of the constant C has been discussed in Section 2 (see Equation (18)). Hence in general, instead of t, one can substitute![]()
.
Now we can rewrite Equations (99) in the following form
![]()
(102)
However, there is still a limitation to be removed: the Boolean functions
![]()
(103)
do not change their structure in the course of dynamics evolution. In order to make their structure plastic while preserving the stability constraints (95) we add a free random term
![]()
(104)
that can be associated with the activation threshold, (compare with Equation (76)).
The governing equations for these terms will be presented in the form of unrestricted random walk, (see Equ- ation (58))
![]()
(105)
with equilibrium values
![]()
(106)
These free terms randomly change the structure of the Boolean functions in course of their dynamics evolu- tion.
Now we can present the proposed model of human mind in the final form
![]()
(107)
![]()
(108)
![]()
(109)
![]()
(110)
The system (107)-(110) is closed and isolated.
Prior to analysis of this model, we have to make a comment concerning the Boolean variables w and the Boo- lean functions B. Strictly speaking, they are not Boolean since they can take three values: −1, 0, 1; however zero values are transitional, and they appear with periodic regularity after each of the values −1 and 1. So if we asso- ciate the proposed dynamics with information processing, the zero values can be ignored since they are fully predictable. The formal difference between the standard Boolean functions taking values 0 and 1 can be removes by a trivial variable transformation.
7. Analysis of the Proposed Model
Starting with Equation (107) and compare it with Equation (93), one concludes that each Boolean variable wi is not affected by the rest of the variables, and the role of the Boolean functions (104) is to provide the stability of the system (107) at ![]()
when![]()
. Therefore the probability dynamics of each Boolean variable is described in Figure 5, and the dynamics of the binary entropy function is described in Figure 6. Figure 5 illu- strates dynamics of probability of the binary evolution of each Boolean variable in Equation (78). Let us assume that the particle is located at the point w = 0 at t = 0. As long as this point is a terminal attractor, the probability is equal to 1. When this point becomes a terminal repeller, the probability splits in two equal parts, and the par- ticle can go right or left with the probability 1/2. It will stay there until this new point becomes a terminal repel- ler, and it moves back to the zero point that is becoming a terminal attractor. This pattern continues indefinitely. It should be emphasized that any two neighboring Boolean values are always separated by a transitional zero point that erases all the memory about the previous values. Since the state space of each Boolean function con- sists of ![]()
configurations, the most convenient quantitative tool for describing Boolean dynamics is the Hum- ming distance.
The Hamming distance between two state configurations of equal length is the number of positions at which the corresponding symbols are different. In another way, it measures the minimum number of substitutions required to change one state configuration in into the other. Due to the property of the Boolean dynamics pointed out above, any two strings of configurations at different times are separated by transitional zero points, and therefore, are uncorrelated.
Let us calculate the probability that two neighboring configuration sequences have zero Humming distance. This event can happen if all n Boolean variables stay at the same places during the next cycle. Since each variable can stay or change with the same probability 1/2, the probability of the event is
![]()
(111)
where ![]()
is the Humming distance.
Then
![]()
(112)
The minimum probability that two configuration strings have the Humming distance ![]()
is illustrated in Figure 7. If the Humming distance is associate with the entropy (the larger the Humming distance the larger the disorder), then the curve in Figure 7 can be compared, at least qualitatively, with the curve in Figure 6: both cases describe dynamics when the process starts with the order, then moves to a disorder, and finally returns to the order. Each cycle in this dynamics is separated from the previous one by a zero transitional state at which all information is erased, and that makes the strings of configurations uncorrelated.
As follows from Equation (104), the values of the Boolean functions Bi change with changes of the corres- ponding Boolean variables. But in addition to that, they also change because the Boolean functions are changed themselves due to additional random inputs![]()
. Therefore dynamics of the system (107) consists of a sequence of uncorrelated two-step cycles during which a new values of the Boolean functions are exposed. It should be recalled that in terms of mathematical logic, each Boolean function is characterized by the truth table, [4] , which is simply a list of all the values of the function at ![]()
values of its arguments. If these arguments are listed in a certain order, every Boolean function has a unique truth table, and as a consequence, the same logical meaning. In this context, the dynamics spontaneously generates new uncorrelated logical statements that expose a choice for making common sense decisions.
The system (107), (108) can be expanded to introduce a new generation of Boolean functions ![]()
based upon the old Boolean functions ![]()
as arguments, and thereby broaden the choice and complexity of the logical statements available for making appropriate decisions
![]()
(113)
![]()
(114)
In the same way, next generations of Boolean functions ![]()
etc. can be introduces. As a result, the pro- posed model is represented as a chain of slave equations ruled by the master Equations (100) and (101). The whole system is isolated, although each of the slave equation taken separately is closed, but not isolated.
8. Discussion and Conclusion
The objective of this work is to extend the model of a hypothetical particle of life [1] , to include the capability to process discrete events dynamics. This capability opens up a way to capture some specific activity of human mind such as information processing via language and logic. The main target of this activity is a mysterious machinery of common sense. It was well understood that rational human behavior, and in particular, the decision making process, is governed by feedbacks from the external world, and this part of the problem was successfully simulated in the most sophisticated way by control systems. However, in addition to that, when the external
![]()
Figure 7. The minimum probability that two configuration strings have the Humming distance![]()
.
world does not provide sufficient information, a human turns for an “advise” to his experience, and that is asso- ciated with a common sense.
Therefore the first challenge of our objective is to preserve isolation of the model of mind from the external world. Such idealization simplifies mathematical formalism without diminishing the proof of concept.
The second challenge is to preserve locality of the model of mind as a part of L-particle: since the known laws of physics are all local, and because nonlocal interactions combined with relativity lead to causal paradoxes, many physicists find nonlocal models unacceptable. However to present a discrete-event dynamics in a local way is a formidable problem: all existing approaches to discrete event dynamics are nonlocal.
Adopting terminology of computer science, we will associate brain with a computer, and mind―with a set of algorithms implemented by the brain. This allows us to distance ourselves from biological aspects of brain and concentrate on intrinsic mathematical properties of mind. And this leads us to the third challenge: to derive the model of human mind based only upon one assumption―the ability to move from disorder to order without ex- ternal sources, i.e. in violation of the second law of thermodynamics. Starting with that postulate, mathematical formalism is supposed to take over and lead to a quantum-inspired model of mind.
Based upon these objective and challenges, this work proposes a mathematical formalism for describing the machinery of human mind creativity. Since some functions of mind support discreteness of cognition, but others support its continuity, while time in physics is always continuous, an attempt to overcome the continuous/dis- crete duality of mind performance is implemented via utilization of special critical points: terminal attractors and repellers that act as autonomous biological clock. In this paper, attention is concentrated upon the discrete mode of the mind activity since the continuous mode was introduced and discussed in details in our previous publica- tions.
The fundamental novelty of the model is in its capability to move from disorder to order without external in- puts in violation of the second law of thermodynamics; that suggests that this kind of dynamics requires exten- sion of modern physics to include physics of life. Conceptually the discrete model links to its continuous version represented by a hypothetical particle of life that is briefly discussed prior to derivation of the discrete model. However, the discrete model should be considered as the next step in study of mind dynamics since it provides a bridge to mathematical origin of self-generated novelties in such brunches as mathematical logic and linguistic, i.e. the highest level activities of human mind.
The proposed model deals with rules of mind activity rather than with its content, i.e. with grammar, but not semantic.
The model is represented by a system of differential equations with terminal attractors and repellers that pro- vide the capability to process discrete-event-based flow of information. This system has master-slave architec- ture: the master equations (see Equations (109) and (110)) describe dynamics of the corresponding L-particle, while the slave equations (see Equations (107), (108), (113) and (114)) present dynamics of Boolean functions that capture the mind activity such as mathematical logic and linguistic. The Boolean dynamics consists of a se- quence of two-step cycles during which a new values of the uncorrelated Boolean functions are exposed. It should be recalled that in terms of mathematical logic, each Boolean function is characterized by the truth table, [4] , which is simply a list of all the values of the function at ![]()
values of its arguments. If these arguments are listed in a certain order, every Boolean function has a unique truth table, and as a consequence, the same logical meaning. In this context, the dynamics spontaneously generates new uncorrelated logical statements that expose a choice for making common sense decisions.
The chain of slave equations can be extended thereby generating new logical statements.
From the thermodynamics viewpoint, during each cycle, entropy of the slave system first grows from zero, and then drops back to zero. Such behavior does not violate the second law of thermodynamics since the slave system is not isolated, although it is closed: It exchanges energy with the master system describing L-particle. However the whole system that includes the master and slave equations is isolated, and nevertheless it generates new logical statements, new patterns of behavior and new information, and that violates the second law of ther- modynamics. It should be emphasized that such a unique property of L-particle is due to the feedback from the Liouville Equation (110) representing the mental dynamics, to Equation (109) representing the motor dynamics. This feedback implements a new type of force―the information force that does not exist neither in Newtonian nor in quantum mechanics (Figure 1). Since the proposed model of human mind, along with L-particle, being a quantum-classical hybrid, acquires non-Newtonian and non-quantum properties, it does not belong to the phys- ics matter as we know it: the modern physics should be complemented with the concept of the information force that represents a bridge between non-living and living matter.