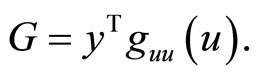1. Introduction
Chen [1] was the first to identify second-order dual formulated for a constrained variational problem and established various duality results under an involved invexitylike assumptions. Husain et al. [2] have presented MondWeir type second-order duality for the problem of [1] and by introducing continuous-time version of secondorder invexity and generalized second-order invexity, validated various duality results. Subsequently, for a class of nondifferentiable continuous programming problems, Husain and Masoodi [3] studied Wolfe type second-order duality while Husain and Srivastava [4] investigated MondWeir type second-order duality. Recently, in the spirit of Mangasarian [5], Husain and Masoodi [6] studied Wolfe type second-order duality for a continuous programming problem having support functions appearing in the integrand of the functional as well as in the constraint functions under second-order invexity and second-order pseudoinvexity conditions. They also incorporated a pair of second-order dual variational problems with natural boundary values rather than fixed end points and indicated their close relationship with those of corresponding (static) second-order duality results established for nonlinear programming problem with support functions, considered by Husain et al. [7]. The popularity of this type of nondifferentiable continuous programming problems seems to originate from the fact that, even though the objective function and/or constraint functions are non-smooth, a simple representation of the dual problem may be written. The theory of non-smooth mathematical programming deals with more general type of functions by means of generalized subdifferentials. However, square root of positive semi-definite quadratic form and support functions are amongst few cases of the nondifferentiable functions for which one can write down the subdifferentials explicitly.
In this paper, we formulate Mond-Weir type secondorder dual to the continuous programming containing support functions in order to further weaken the secondorder generalized invexity of [6]. Usual duality theorems for this pair of Mond-Weir type second-order dual continuous programming problems are validated under generalized second-order invexity assumptions. Special cases are derived. Further, a pair of Mond-Weir second-order dual variational problems with natural boundary values rather than fixed end points is presented and the proofs of the duality theorems are claimed to follow analogously. It is also pointed out that our second-order duality results can be considered as dynamic generalizations of corresponding (Static) second-order duality results established for nonlinear programming problem with support functions considered by Husain et al. [7].
2. Pre-Requisites
Let 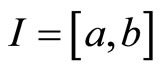 be a real interval
be a real interval 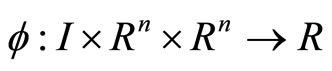 and
and 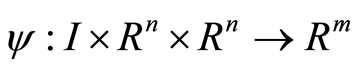 be twice continuously differentiable functions. In order to consider
be twice continuously differentiable functions. In order to consider 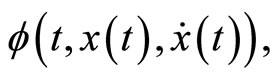 where
where 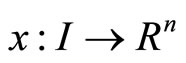 is differentiable with derivative
is differentiable with derivative 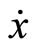 denoted by
denoted by 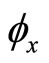 and
and 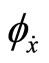 the first order derivative of
the first order derivative of 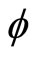 with respect to
with respect to 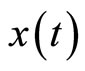 and
and 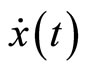 respectively, that is,
respectively, that is,
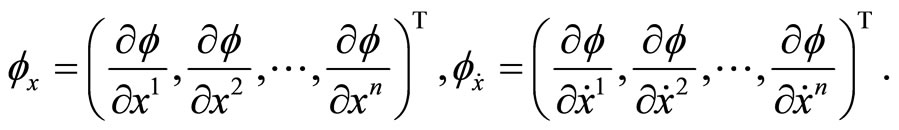
Denote by 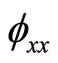 the
the 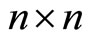 Hessian matrix of
Hessian matrix of 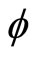 and
and 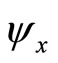 the
the 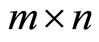 Jacobian matrix respectively, that is, with respect to
Jacobian matrix respectively, that is, with respect to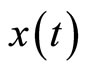 , that is,
, that is,
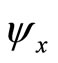
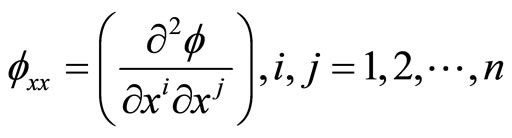 the
the 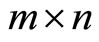 Jacobian matrix.
Jacobian matrix.

The symbols 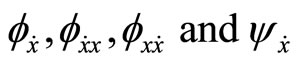 have analogous representations. Designate by X the space of piecewise smooth functions
have analogous representations. Designate by X the space of piecewise smooth functions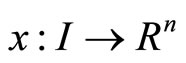 , with the norm
, with the norm
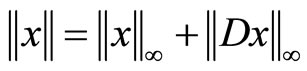 where the differentiation operator
where the differentiation operator 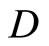
is given by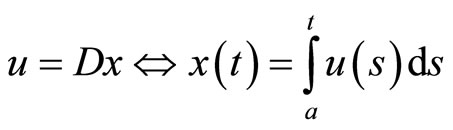 , Thus
, Thus 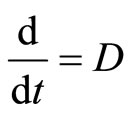 except at discontinuities.
except at discontinuities.
We incorporate the following definitions which needed in the subsequent analysis:
Definition1. (Second-Order Invex):
If there exists a vector function 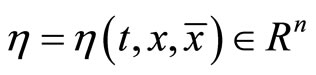 where
where 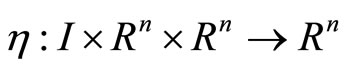 and with
and with 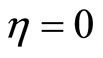 at t = a and t = b such that for a scalar function
at t = a and t = b such that for a scalar function 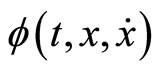 the functional
the functional 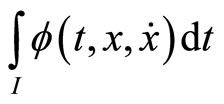 where
where 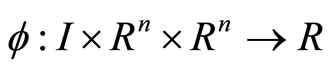
satisfies
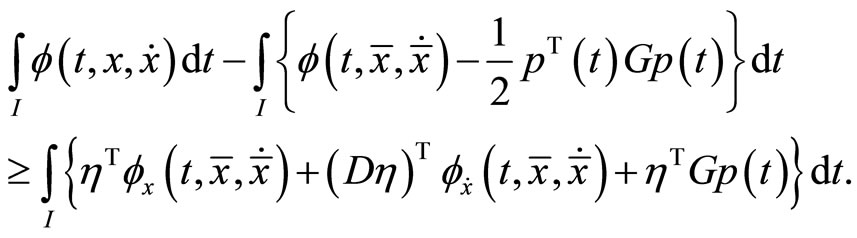
Then 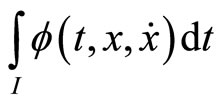 is second-order invex with respect to
is second-order invex with respect to 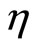 where
where 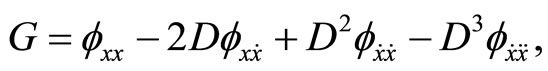
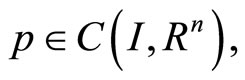 the space of
the space of 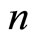 -dimensional continuous vector functions.
-dimensional continuous vector functions.
Definition 2. (Second-Order Pseudoinvex): If the functional 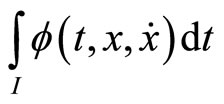 satisfies
satisfies
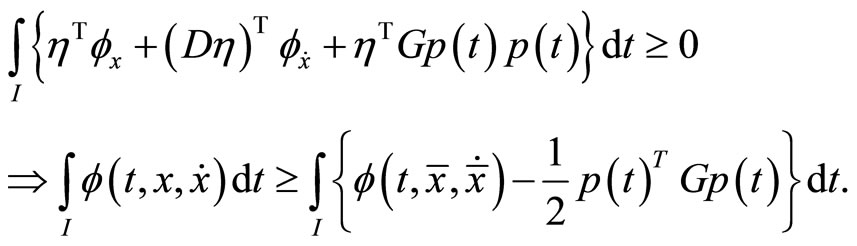
Then 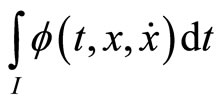 is said to be second-order pseudoinvex with respect to
is said to be second-order pseudoinvex with respect to 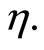
Definition 3. (Second-Order Strictly Pseudoinvex):
If the functional 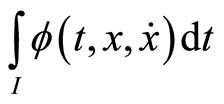 satisfies
satisfies
then 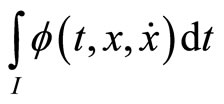 is said to be second-order strictly pseudoinvex with respect to
is said to be second-order strictly pseudoinvex with respect to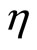 .
.
Definition 4. (Second-Order Quasi-invex):
If the functional 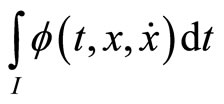 satisfies
satisfies
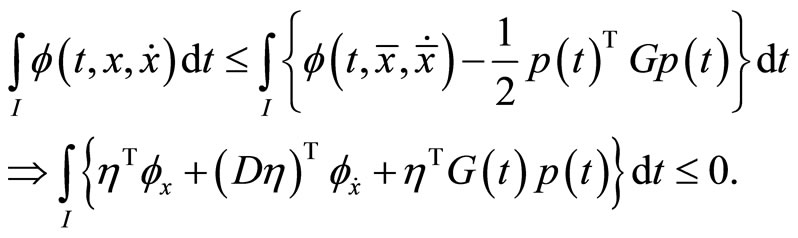
Then 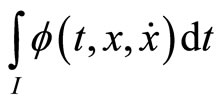 is said to be second-order quasiinvex with respect to
is said to be second-order quasiinvex with respect to 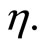
Consider the following nondifferentiable continuous programming problem with support functions treated by Husain and Jabeen [8]:
(CP): Minimize 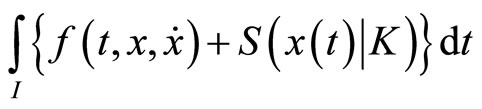
subject to
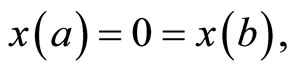 (1)
(1)
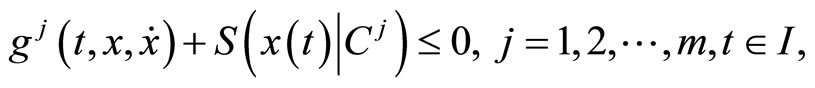 (2)
(2)
where f and g are continuously differentiable and each 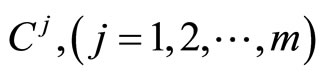 is a compact convex set in
is a compact convex set in 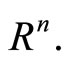
Husain and Jabeen [8] derived the following optimality condition for (CP):
Lemma 1. (Fritz-John Necessary Optimality Conditions):
If the problem (CP) attains a minimum at 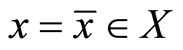 then there exist
then there exist  and piecewise smooth functions
and piecewise smooth functions 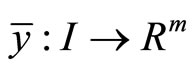 with
with 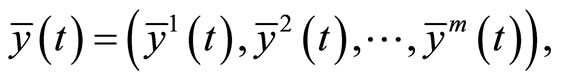
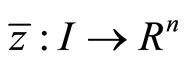 and
and 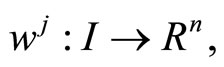
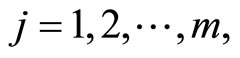 such that
such that
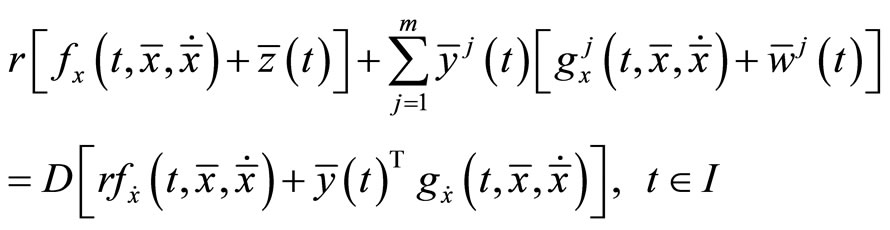
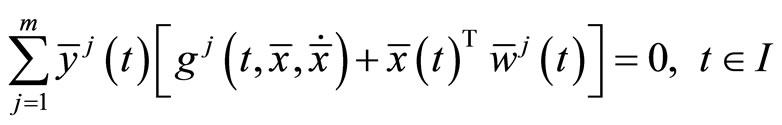
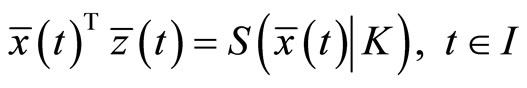
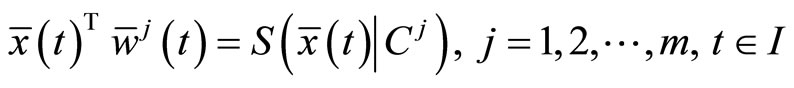
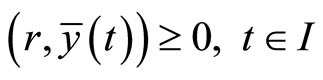
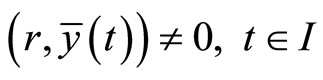
The minimum 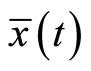 of (CP) may be described as normal if
of (CP) may be described as normal if 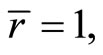 so that the Fritz John optimality conditions reduce to Karush-Kuhn-Tucker optimality conditions. It suffices for
so that the Fritz John optimality conditions reduce to Karush-Kuhn-Tucker optimality conditions. It suffices for 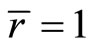 that Slater’s [8] condition holds at
that Slater’s [8] condition holds at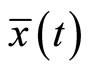 .
.
Now we review some well known facts about a support function for easy reference.
Let K be a compact set in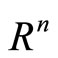 , then the support function of
, then the support function of 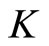 is defined by
is defined by
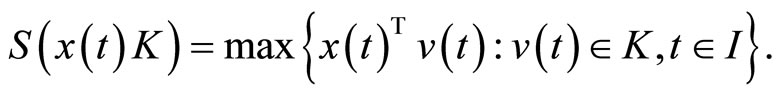
A support function, being convex everywhere finite, has a subdifferential in the sense of convex analysis i.e., there exist 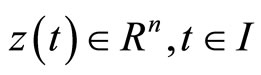 such that
such that
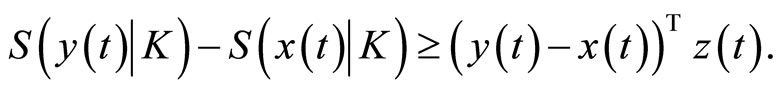
From [9], the subdifferential of 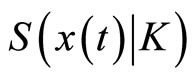 is given by
is given by
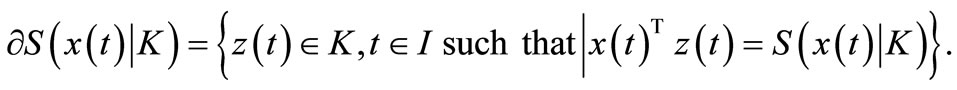
For any set , the normal cone to
, the normal cone to  at a point
at a point  is defined by
is defined by
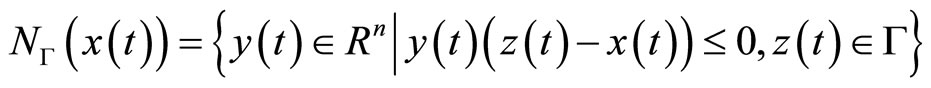
It can be verified that for a compact convex set C, 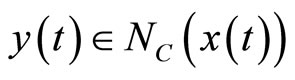 if and only if
if and only if
3. Mond-Weir Type Second-Order Duality
In this section, we present the following problem as the Mond-Weir type dual to (CP) and validate usual duality theorems:
(M-WCD):
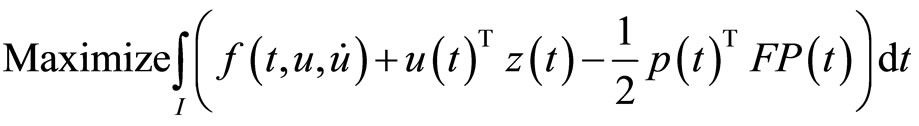
subject to
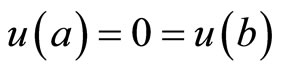 (3)
(3)
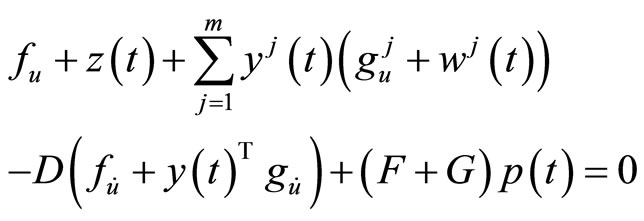 (4)
(4)
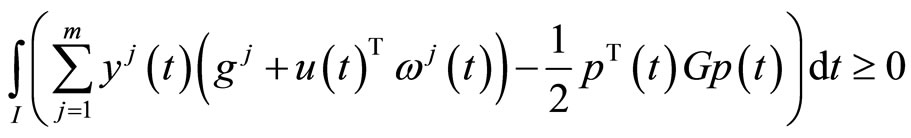 (5)
(5)
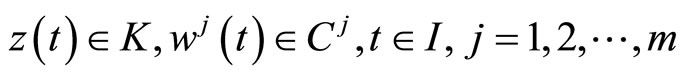 (6)
(6)
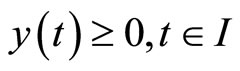 (7)
(7)
where
1) 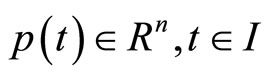
2) 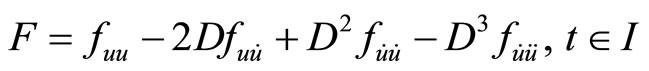
3)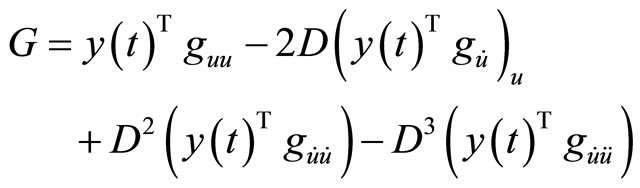
Theorem 1. (Weak Duality): Let 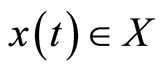 be feasible solution of (CP) and
be feasible solution of (CP) and
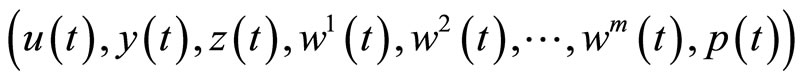
be feasible for (M-WCD). Assume that for all feasible
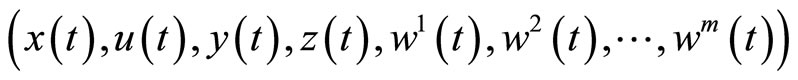
and with respect to vector function 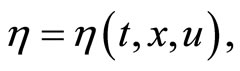
1) 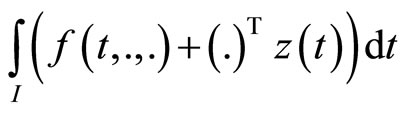 is second-order pseudoinvex and
is second-order pseudoinvex and
2) 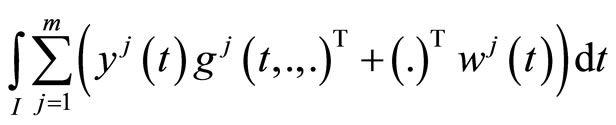 is second-order quasi-invex.
is second-order quasi-invex.
Then,
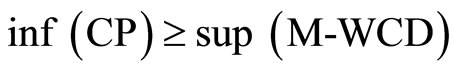 .
.
Proof: Since  is feasible for (CP) and
is feasible for (CP) and
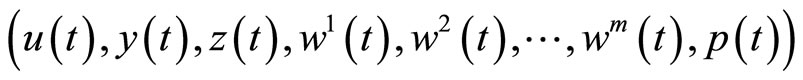
is feasible of (M-WCD), we have
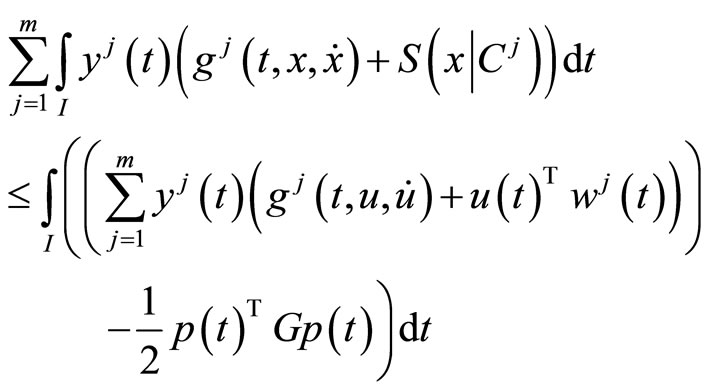
Using 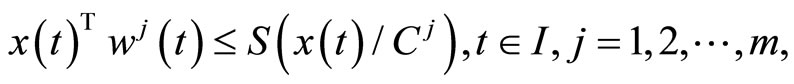 we have,
we have,
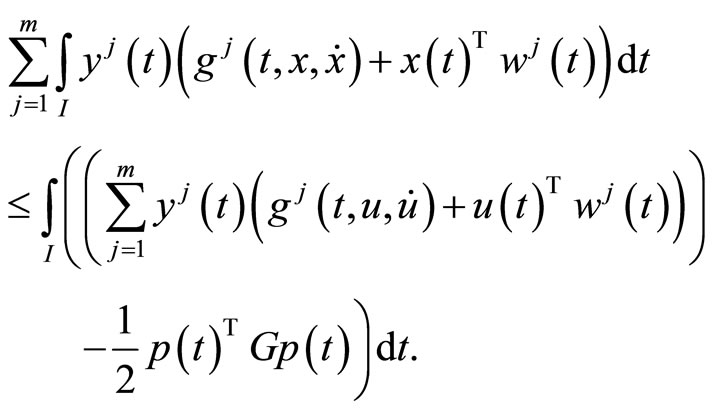
By the second-order quasi-invexity of
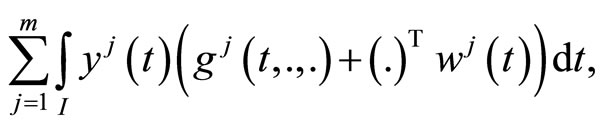
for  with respect to
with respect to  from this we have,
from this we have,
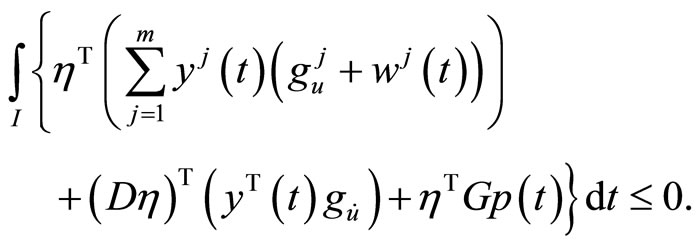
By integrating by parts, we have
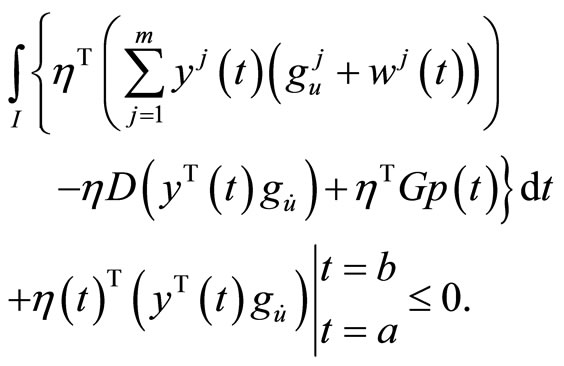
Using 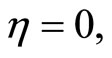 at
at 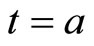 and
and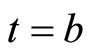 , this yields,
, this yields,
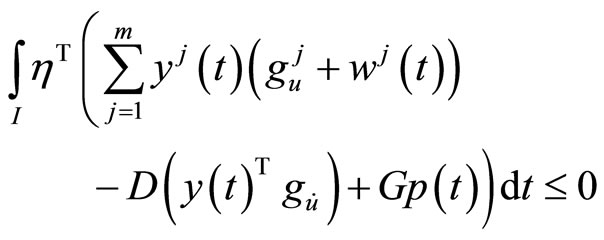
Using equality constraint (4), we have
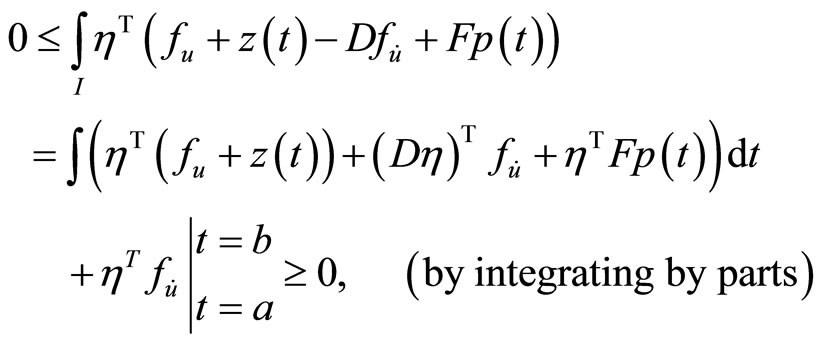
As earlier, this becomes
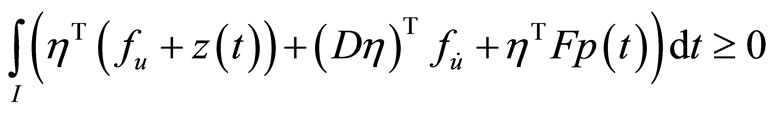
This, because of second-order pseudoinvexity of
 with respect to
with respect to
 gives
gives
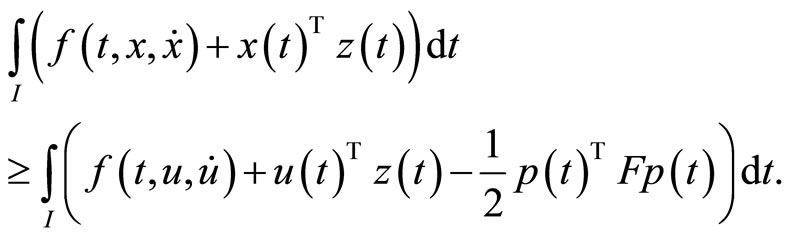
Since 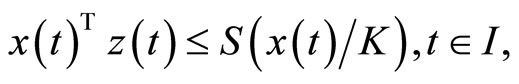 we have
we have
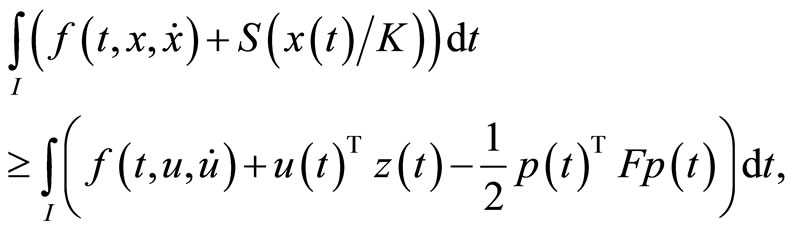
implying,
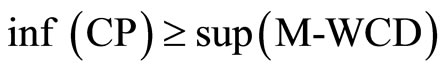 .
.
Theorem 2. (Strong Duality):
If 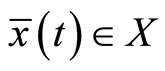 be an optimal solution of (CP) and is normal, then there exist piecewise smooth functions
be an optimal solution of (CP) and is normal, then there exist piecewise smooth functions 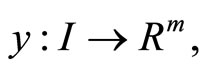
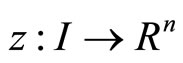 and
and 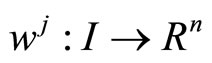 such that
such that 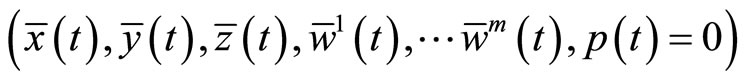 is a feasible solution of (CD) and the two objective values are equal. Furthermore, if the hypothesis of Theorem1 holds, then
is a feasible solution of (CD) and the two objective values are equal. Furthermore, if the hypothesis of Theorem1 holds, then 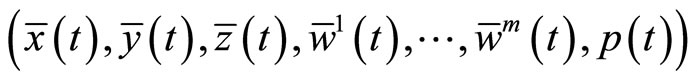 is an optimal solution of (M-WCD).
is an optimal solution of (M-WCD).
Proof: From Lemma 1 there exist piecewise smooth functions 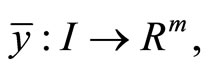
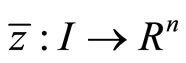 and
and 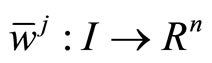
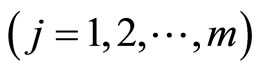 such that
such that
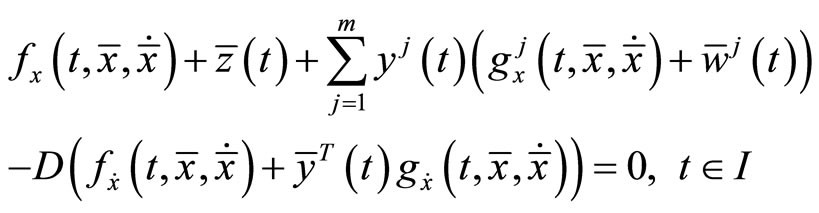
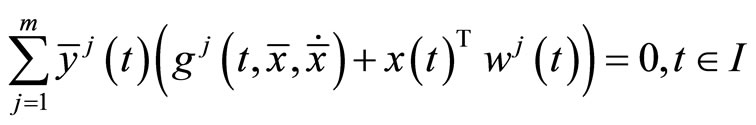
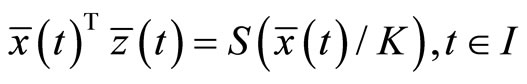
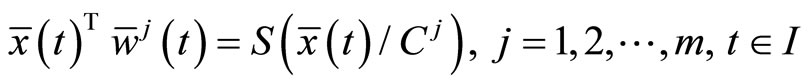
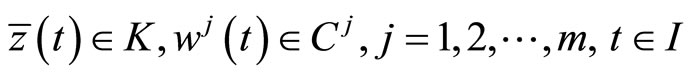
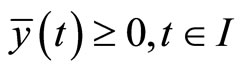
The above relations imply that
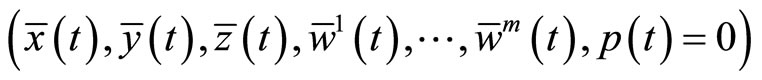 is feasible for (M-WCD).
is feasible for (M-WCD).
Also
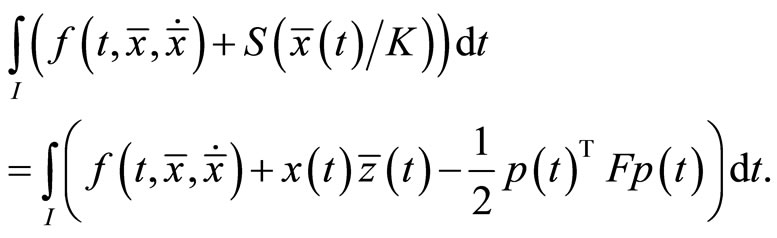
This shows the equality of objective functions of the problem. Hence the optimality of
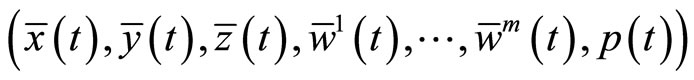 for (M-WCD) follows from weak duality theorem (Theorem1).
for (M-WCD) follows from weak duality theorem (Theorem1).
Theorem 3 (Strict Converse Duality): Assume that
(C1): 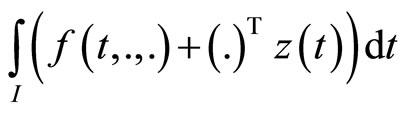 is second-order strictly pseudoinvex and
is second-order strictly pseudoinvex and 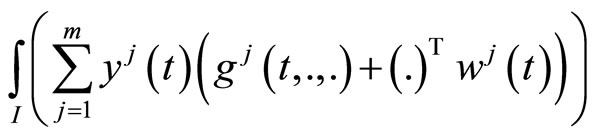 is second-order quasi-invex with respect to the same
is second-order quasi-invex with respect to the same .
.
(C2): 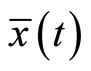 is an optimal solution for (CP), If
is an optimal solution for (CP), If 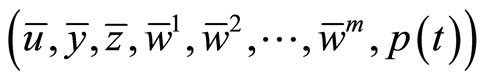 is optimal solution of (MWCD), then
is optimal solution of (MWCD), then 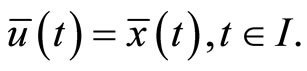
Proof: We assume that 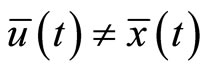 and show that a contradiction follows. Since
and show that a contradiction follows. Since 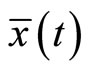 is an optimal solution of (CP), it follows from Theorem 2, there exist
is an optimal solution of (CP), it follows from Theorem 2, there exist 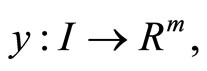
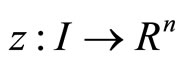 and
and
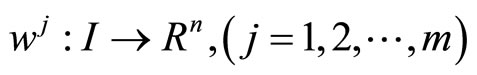 such that
such that
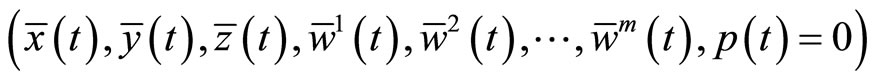
is optimal solution of (M-WCD).
Since
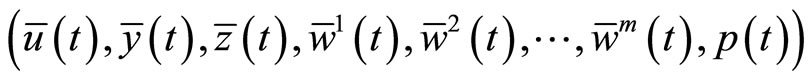
is an optimal solution of (M-WCD), it follows that
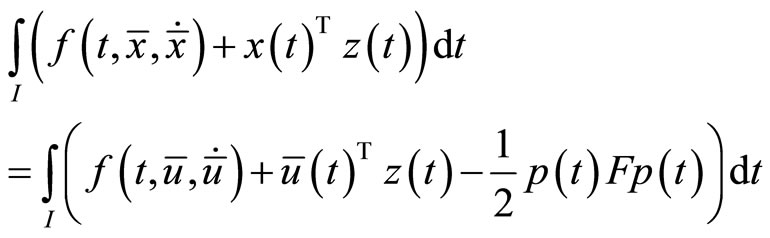
This, because of the second-order strict pseudoinvexity of 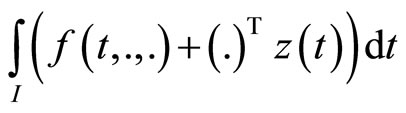 for all
for all 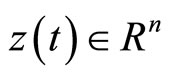 gives
gives
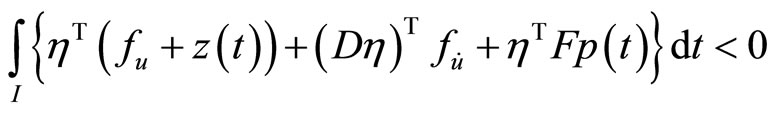 (8)
(8)
From the constraint of (CP) and (M-WCD), we have
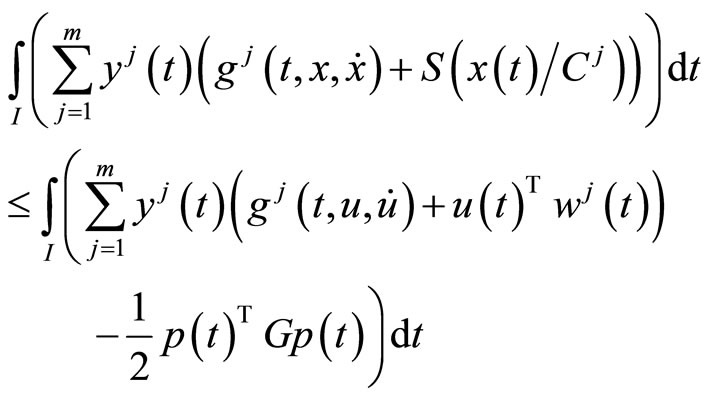
Using 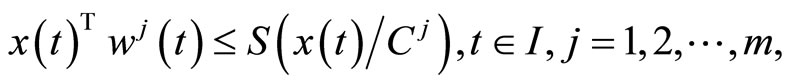
from this, we have
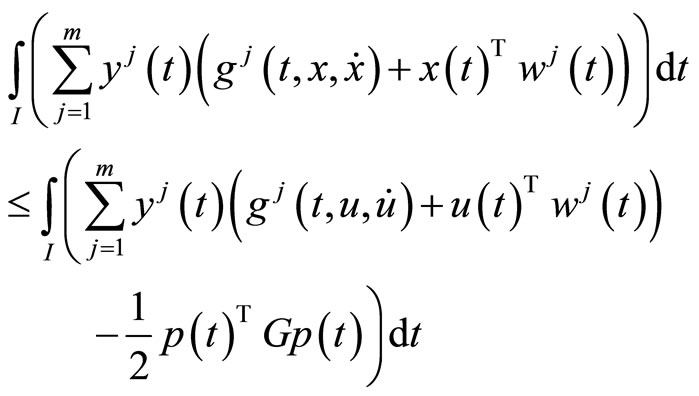
This, because of (C1) we have
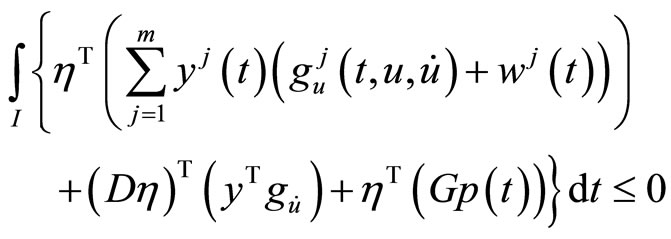 (9)
(9)
Combining (8) and (9), we have
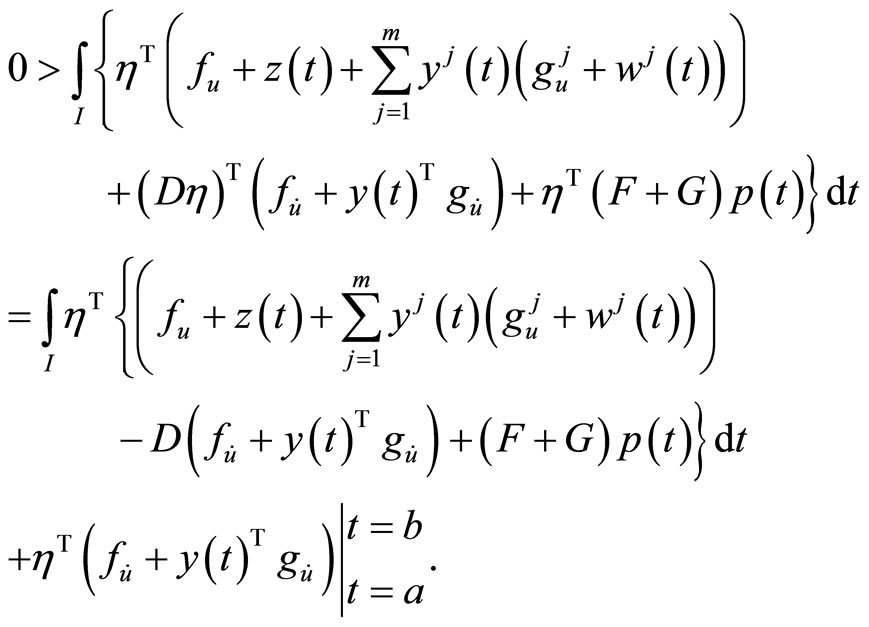
Using 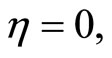 at
at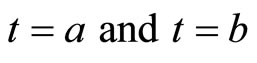 , this implies
, this implies
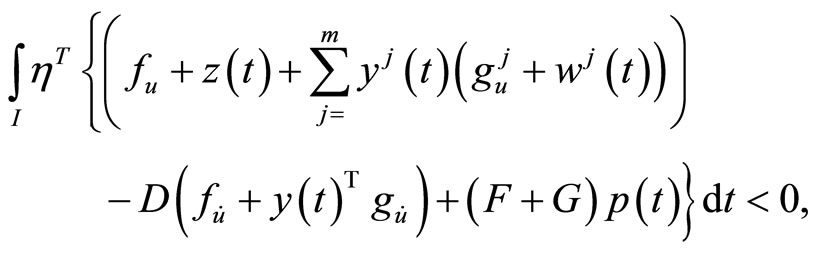
contradicting the equality constraint of (M-WCD), hence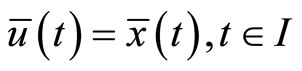 .
.
Theorem 4. (Converse Duality): Assume that
(H1): 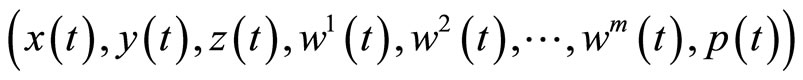
is an optimal solution of (M-WCD).
(H2): The vectors 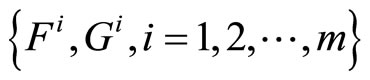 are linear independent where
are linear independent where 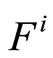 and
and 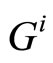 are the ith row of F and G respectively, and
are the ith row of F and G respectively, and
(H3):
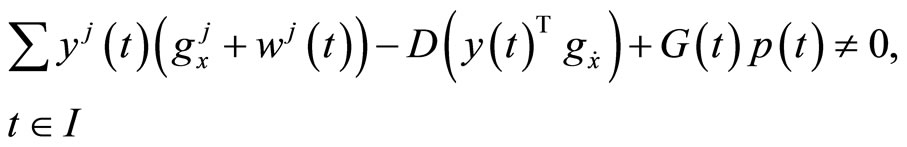
and
(H4): either 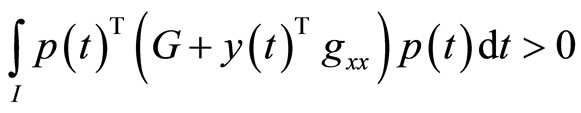
and 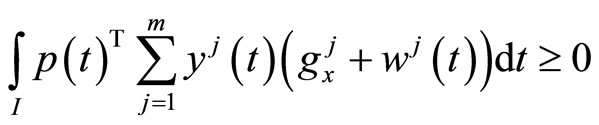
or 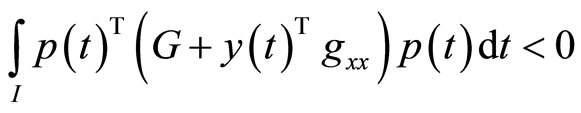
and 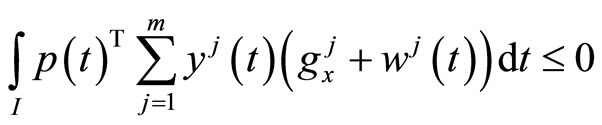
Then 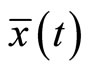 is feasible for (CP) and the two objective functionals have the same value. Also, if Theorem1 holds for all feasible solution of (CP) and (M-WCD), then
is feasible for (CP) and the two objective functionals have the same value. Also, if Theorem1 holds for all feasible solution of (CP) and (M-WCD), then 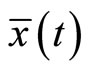 is an optimal solution of (CP).
is an optimal solution of (CP).
Proof: Since
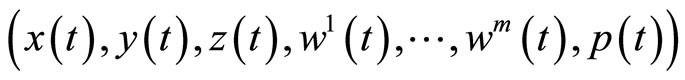 is an optimal solution of (M-WCD), by results of Schester [10], there exists
is an optimal solution of (M-WCD), by results of Schester [10], there exists 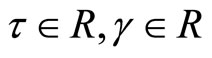 and piecewise smooth function
and piecewise smooth function 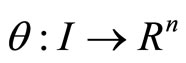 and
and 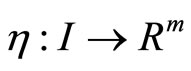 such that following Fritz John optimality conditions are satisfied:
such that following Fritz John optimality conditions are satisfied:
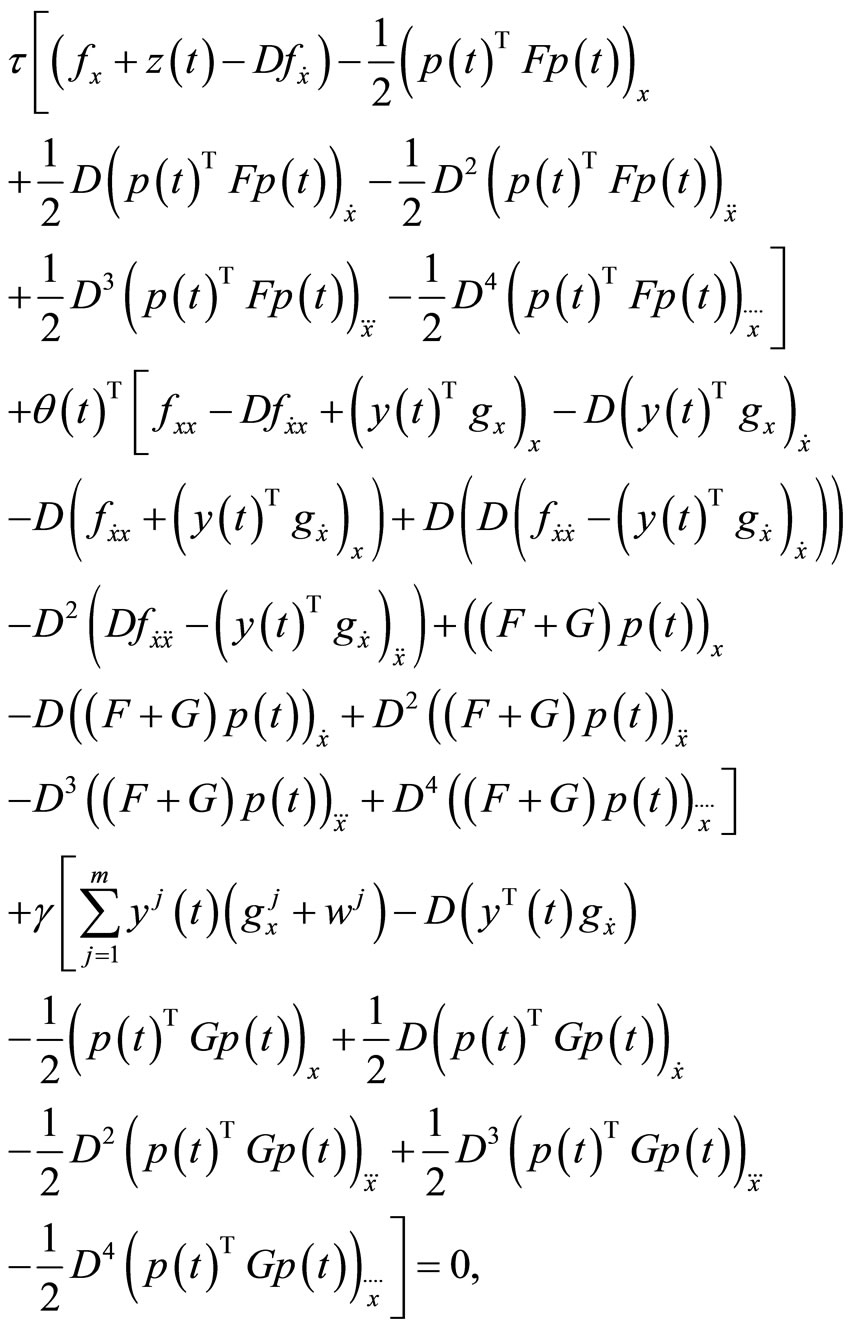 (10)
(10)
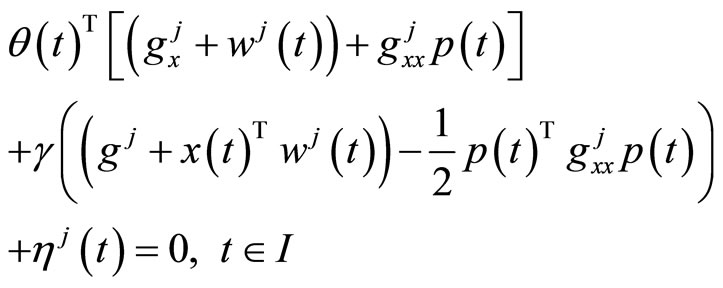 (11)
(11)
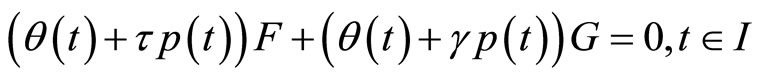 (12)
(12)
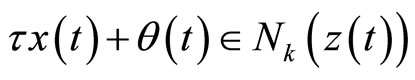 (13)
(13)
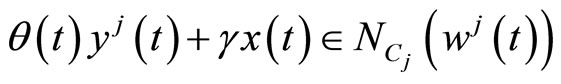 (14)
(14)
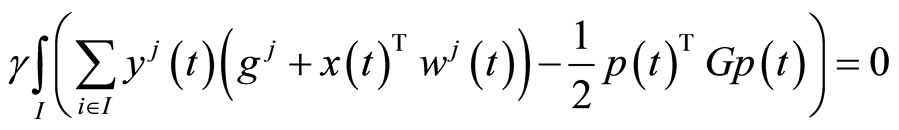 (15)
(15)
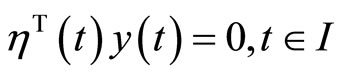 (16)
(16)
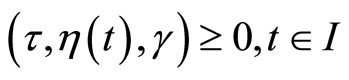 (17)
(17)
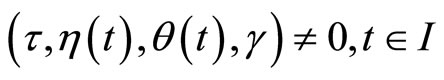 (18)
(18)
Using the hypothesis (H2) in (12), we have
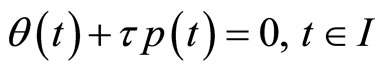 (19)
(19)
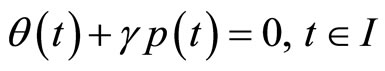 (20)
(20)
Using (4), (19) and (20) in (10), we have (see (21) below)
Let  then (20) gives
then (20) gives 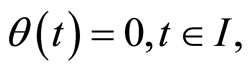 (19) implies
(19) implies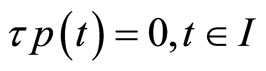 .
.
Consequently from (21), we have
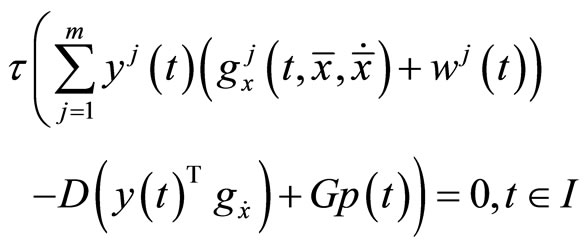
By the hypothesis (H3), this implies 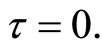
The relation (11) implies 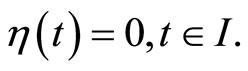
Hence 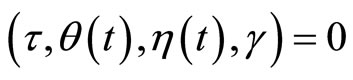 contradicting the Fritz John condition, Hence
contradicting the Fritz John condition, Hence 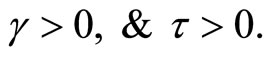
Pre-multiplying (11) by 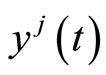 and Using (16), we have
and Using (16), we have
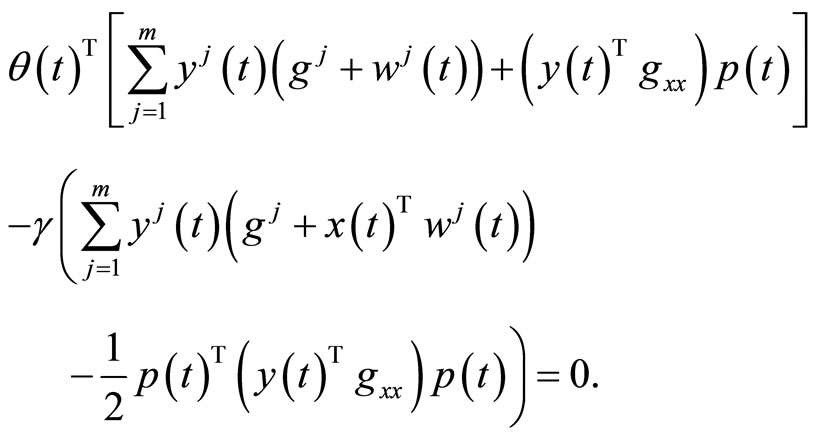
Integrating and then using (15), we have
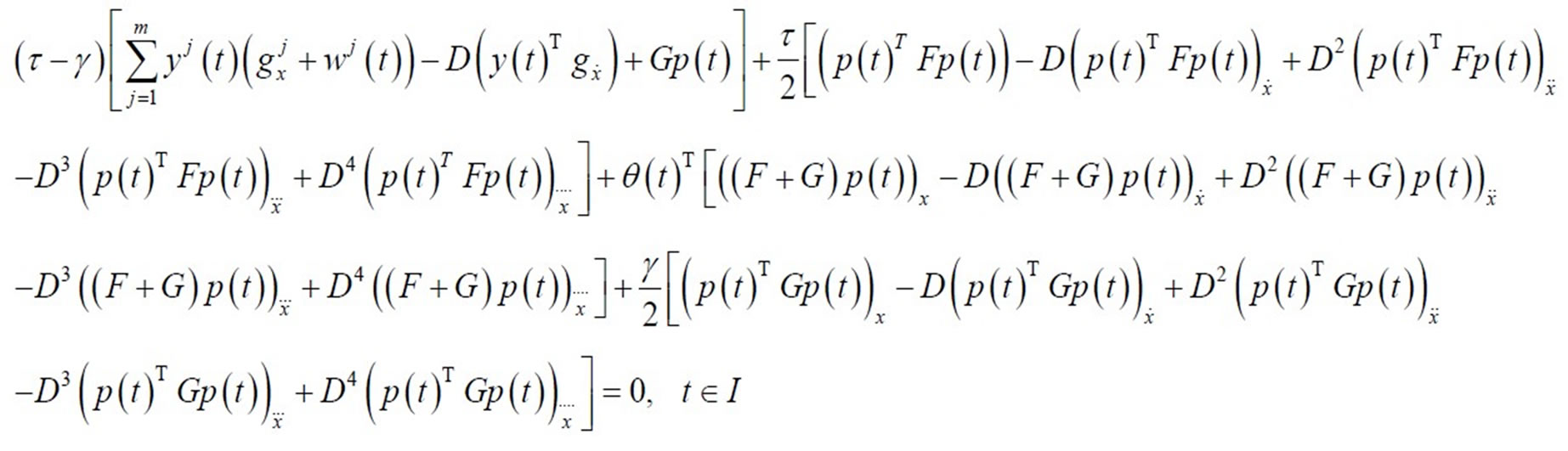 (21)
(21)
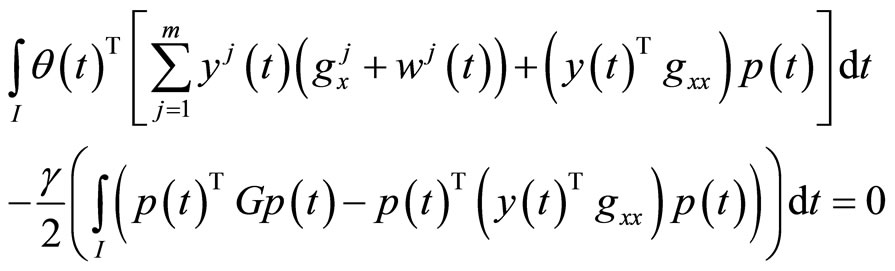
Putting 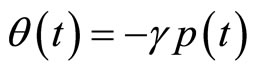 we have
we have
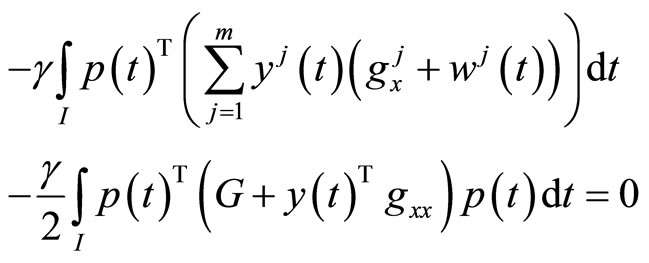
gives
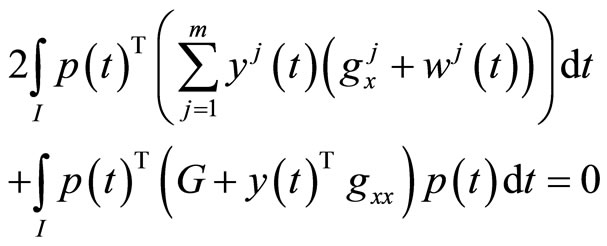
This, in view of the hypothesis (H4) yields, 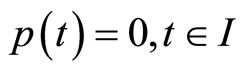 we have
we have 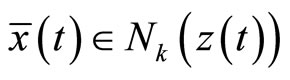 and
and
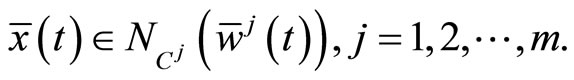
These respectively imply 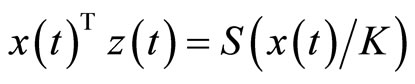 and
and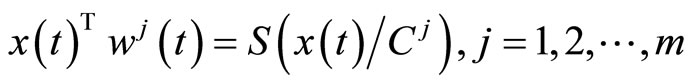 .
.
Multiplying the relation (11) by 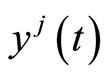 and using (16) along with
and using (16) along with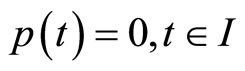 , we have
, we have
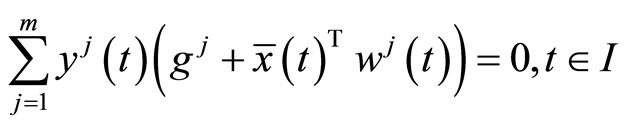
and also 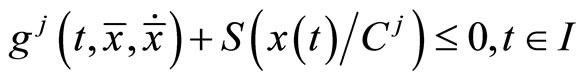 implying the feasibility of
implying the feasibility of 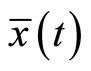 for (CP).
for (CP).
Finally,
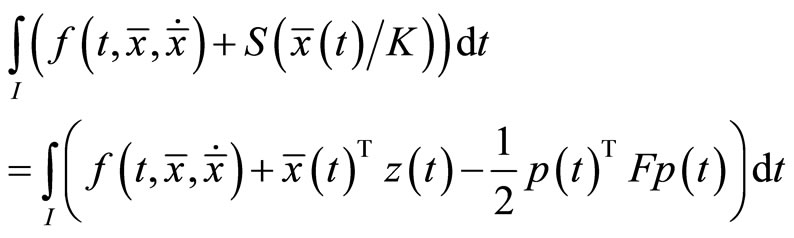
By Theorem 1, it implies that 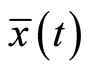 is an optimal solution of (CP).
is an optimal solution of (CP).
4. Special Cases
Let for 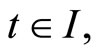
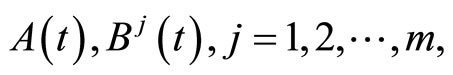 be positive semidefinite matrices and continuous on
be positive semidefinite matrices and continuous on 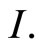
Then 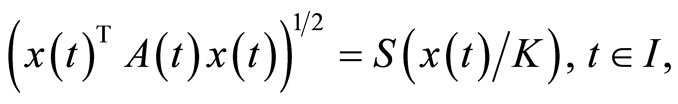 where
where
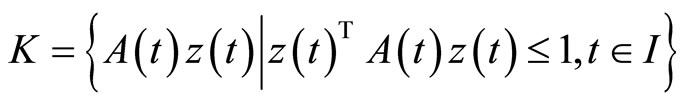
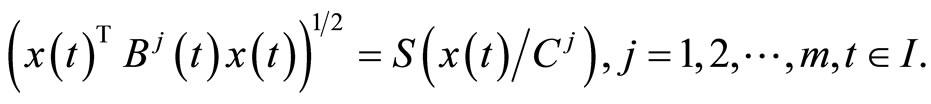
Replacing 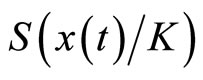 by
by 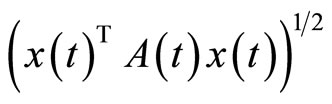 and
and
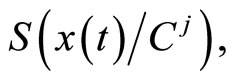 by
by
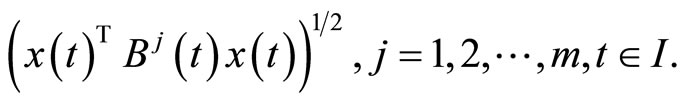
We have the following problems:
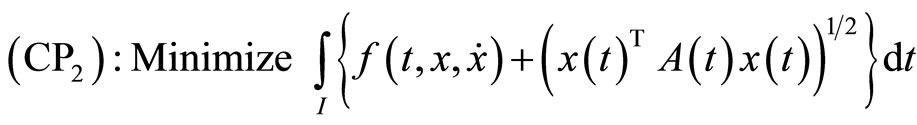
subject to
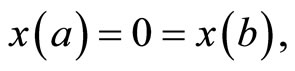
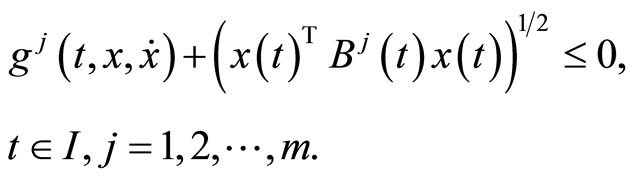
(M-WCD2):
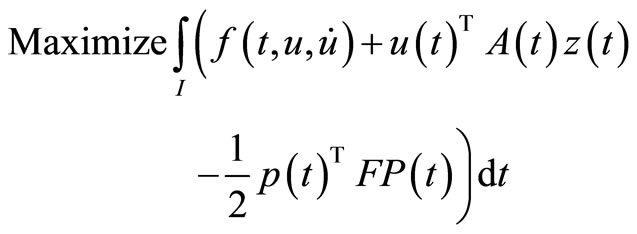
subject to
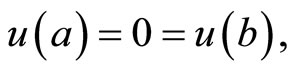
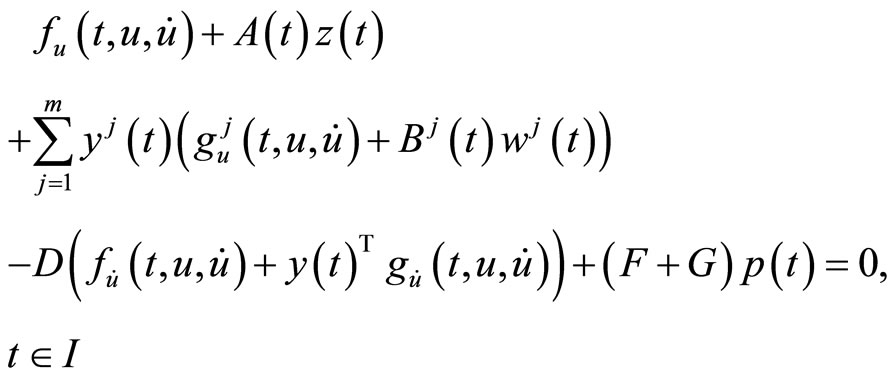
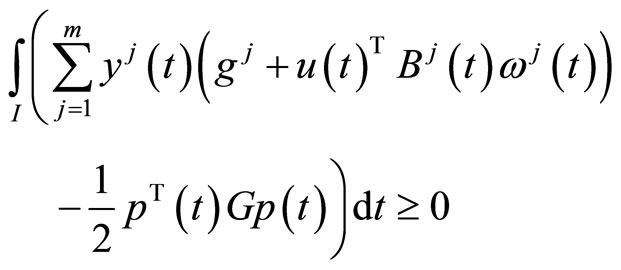
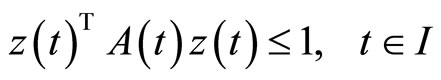
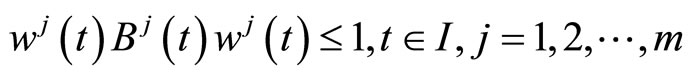
If 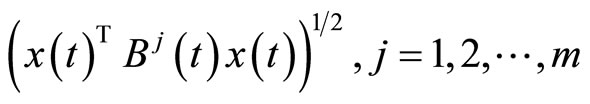 are suppressed from the constraints of (CP2), we have the following problem studied for duality by Husain and Srivastava [4].
are suppressed from the constraints of (CP2), we have the following problem studied for duality by Husain and Srivastava [4].
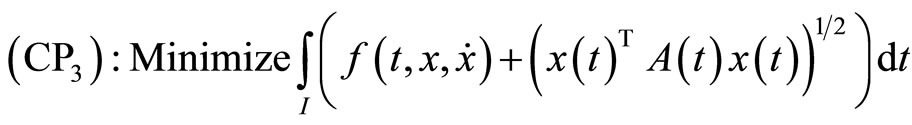
subject to
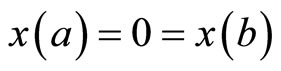
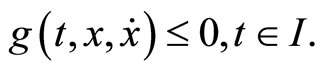
(M-WCD3):
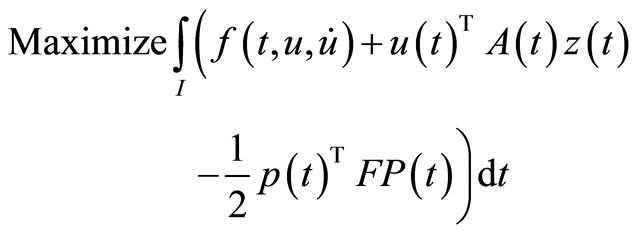
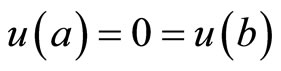
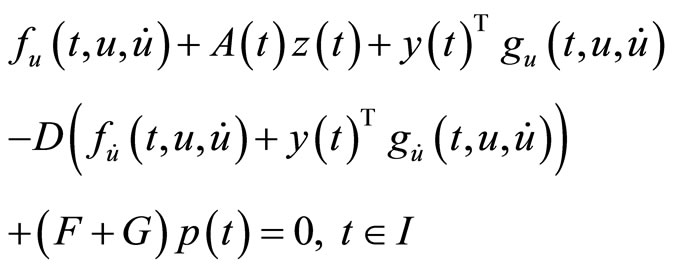
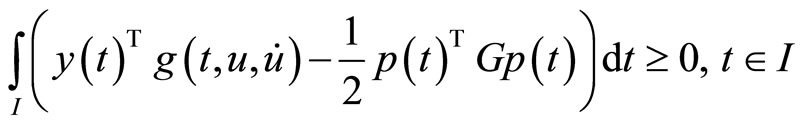
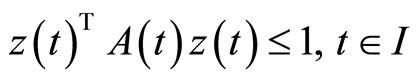
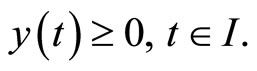
5. Problems with Natural Boundary Values
In this section, we formulate a pair of nondifferentiable dual variational problems with natural boundary values rather than fixed end points.
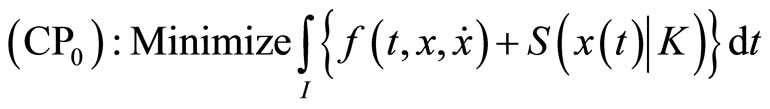
subject to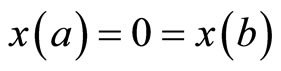 ,
,
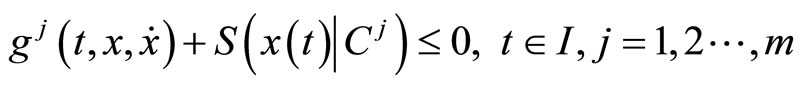
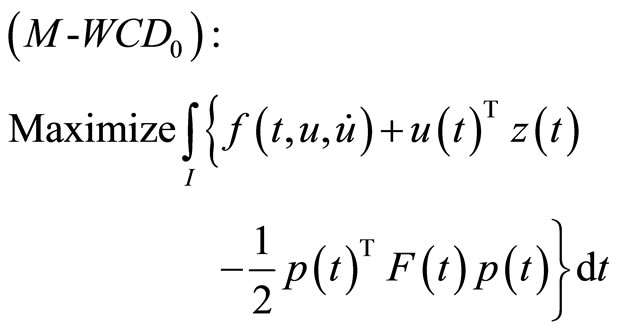
subject to
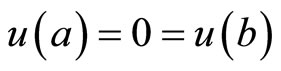
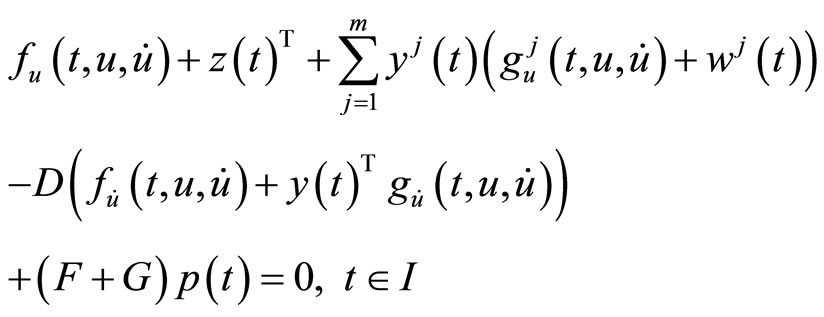
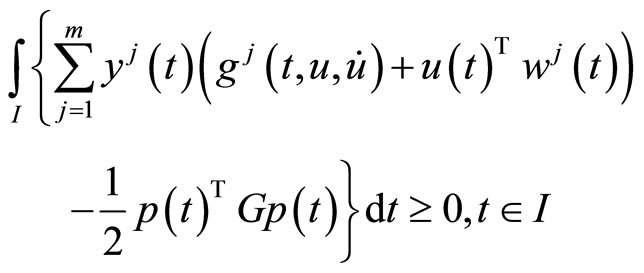
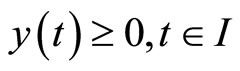
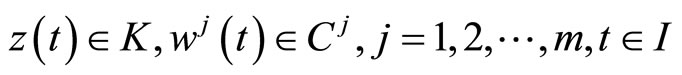
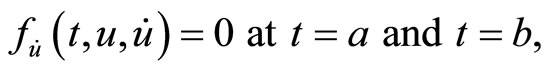
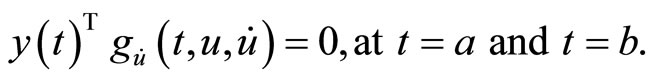
6. Nonlinear Programming Problems
If all functions in the problems (CP0) and (M-WCD0) are independent of t, then these problems will reduce to the following nonlinear programming problems studied by Husain et al. [7].
(CP1): Minimize 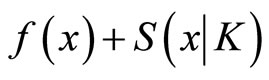
subject to
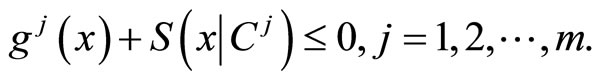
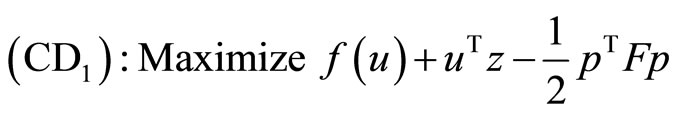
subject to
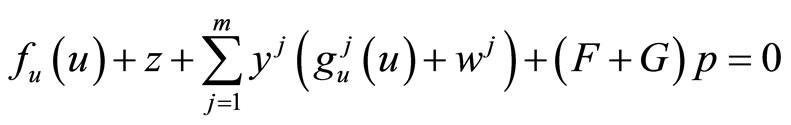
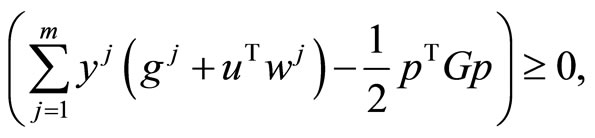
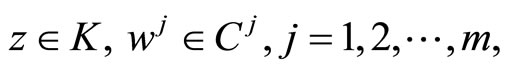
where 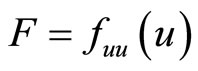 and
and