World Journal of Engineering and Technology
Vol.07 No.04(2019), Article ID:96325,9 pages
10.4236/wjet.2019.74B001
Temperature Research of Permanent Magnet Brushless DC Motor for Electric Balanced Vehicle
Baoguo Wang, Jiangui Li, Dong Ai
School of Mechanical and Electronic Engineering, Wuhan University of Technology, Wuhan, China




Received: April 29, 2019; Accepted: November 10, 2019; Published: November 13, 2019
ABSTRACT
A power system structure composed of a brushless DC motor and a cycloidal reducer for electric balanced vehicle has been proposed, and the temperature of important components in this structure would be discussed. The loss generated by the cycloid reducer is negligible, it’s only need to analyze the thermal field of motor. Since the temperature change will affect the material properties of the target motor, the electromagnetic and temperature fields, involved in the motor, are selected for coupling calculation to determine whether the final temperature distribution can meet the requirements of vehicle for use.
Keywords:
Electric Balanced Vehicle, Permanent Magnet Brushless DC Motor, Cycloidal Pinwheel Reducer, Multiphysics Coupling

1. Introduction
Recently, with the growing concern of serious environmental problem caused by the internal combustion engine vehicles, the government is planning to forbid the manufacture of the internal combustion engine vehicles. Therefore, the cleaner, more efficient and sustainable cars have attracted much attention in recent years [1] [2]. Due to the zero-emission nature of the electric vehicle, it is recognized as the most viable actuator to replace the combustion engine driving system in traditional vehicles.
The self-balanced vehicle system can be thought as a simple robot driven by the motor [3]. Therefore, it’s necessary to carry out relevant analysis to the motor. The loss generated by rotating motor will lead to the temperature increase of the motor, through different forms of heat transfer. If the operating temperature of the motor is too high, it will cause a lot of problems [4] [5] [6], such as breakdown of stator winding, even invalidation of winding protection; demagnetization of permanent magnets; ruin of insulation in silicon steel; impairment of bearings along with main load parts and so on. Aiming to ensure the stable operation performance of the motor, it’s important to keep the motor temperature within acceptable range.
2. Parameters and Structure of Power System
The integrated driving system is consisted of a middle speed permanent-magnet DC motor and a cycloidal reducer. The motor is designed to have enough central space to accommodate the cycloidal reducer. The cycloidal disc, eccentric disc, roller gear pins and bushes, along with ring gear pins and bushes make up the cycloidal reducer, as shown in Figure 1. The cycloidal reducer is integrated coaxially into the inner space of stator to convert the high speed of the rotor to the low speed of the shaft and reduce the vibration of the vehicle. The output shaft of cycloidal reducer is attached to the left side of input shaft of cycloidal reducer. The torque is transmitted through the ring gear, cycloidal disc, and roller gear, and then the torque is exported by the output shaft.
Comparing with the motor used in existed electric balanced vehicle, the rotating speed of motor in this paper is relatively high to improve the power efficiency and power density. The cycloidal reducer has been adopted to convert the high speed of the motor to the low speed of the wheel and reduce the vibration, making the electric balanced vehicle more stabilized and safety. The axial length of system would not be increased by mounting the whole cycloidal reducer into the inner space of stator.
The driving force provided by motor is to overcome the resistance of vehicle during moving. The resistance is composed of air resistance Fw, rolling resistance Fr and slope resistance Fs [7]. When the vehicle is running at a constant speed and the wind speed is zero, the power provided by the motor is in equilibrium with these resistances, the relationship can be expressed by:
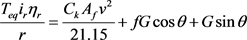 (1)
(1)
where, Teq is the output torque of drive motor; ηr is the transmission efficiency of reducer; ir is the transmission ratio of reducer; r is the radius of vehicle wheel; Ck is the air resistance coefficient; Af is the frontal area of the balanced vehicle and rider; ρ is the air density; vr is relative air speed to unicycle; G is the gravity of balanced vehicle and rider; θ is the actual road slope angle; f is the rolling resistance coefficient.
The fundamental parameters of motor are determined by the torque and speed of vehicle under extreme driving conditions, the specific design data of electric balanced vehicle are listed in Table 1.
The transmission ratio is chosen to be 11, the input rotating speed is 1500 r/min. This two data are substituted into formula 1, the function of torque with riding speed and road slope is shown in Figure 2.
Figure 1. Proposed system. (a) Sectional view of the cycloidal reducer; (b) Schematic assembly of the motor with cycloidal reducer.
Figure 2. Torque required vs unicycle speed at different slopes.
Table 1. Parameters of the electric balanced vehicle.
The maximum motor torque required for unicycle approaches approximately 12 Nm at point A, when the unicycle is running on a maximum slope of 20˚. The output torque is calculated by:
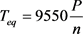 (2)
(2)
where, P is the rated power of motor; n is the rated rotating speed of motor.
Teq and n are substituted into formula 2 to calculate the maximum motor power. The rated power of motor is selected to be 2.2 kW, and then the fundamental parameters of motor are shown in Table 2.
3. Loss Calculation of Permanent Magnet Motor
The magnetic circuit model is built to calculate the loss of motor according to the design parameters obtained in the front.
1) Core loss
At present, the most recognized and widely used in core loss calculation is the classical separation model of alternating loss proposed by A. Bertotti [8]. The loss is divided into three sections to calculate separately, the core loss in sinusoidal flux excitation is calculated by:
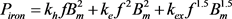 (3)
(3)
where Bm is the flux density in the core of motor; f is the alternating frequency of the magnetic field; kh is the coefficient of hysteresis loss of motor; kc is the coefficient of eddy current loss; and ke is the coefficient of excess loss.
2) Copper loss
Copper loss is generated by the current through the stator winding, it is subscribed as:
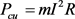 (4)
(4)
where, m is the number of winding phase; I is the valid value of phase current; R is the phase winding resistance.
3) Eddy current loss
The eddy current loss produced by permanent magnet is:
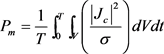 (5)
(5)
Table 2. The parameters of motor.
where, Jc is eddy current density; σm is permanent magnet conductivity; V is permanent magnet volume.
4) Mechanical loss
The mechanical loss is consisted of ventilation loss and friction loss, it’s usually obtained by empirical formula.
a) Ventilation loss
The ventilation loss caused by the rotational motion of rotor is expressed by:
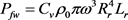 (6)
(6)
where, Cv is coefficient of friction; ρ0 is density of surrounding medium; Rr is rotor radium; Lr is axial length of rotor.
b) Friction loss
The friction loss is generated by the rotating part with bearings, due to the friction between them, it is calculated by:
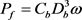 (7)
(7)
where, Cb is the friction coefficient of bearing; Db is bearing diameter.
The core loss is always viewed as constant when the load is changeable, it only varies with the change of speed. So the loss variation of motor at different speed is studied in this paper. Table 3 shows the motor copper loss, permanent magnet eddy current loss and mechanical loss value calculated by the previous formula at different speed of the motor.
It can be found that the core loss, eddy current loss and mechanical loss are proportional to the speed, and the infection is bigger when the speed is higher. The copper loss changes little while the rotating speed is increasing, it implies that the speed changing has almost no effect on the value of copper loss.
4. Thermal Analysis of Permanent Magnet Motor
4.1. The Calculation of Thermal Conductivity
It’s difficult to calculate the heat transfer according to the actual situation because of the irregular shape of conductor in solving domain [9]. The equivalent thermal conductivity is used to simplify the thermal model of motor. Table 4 shows the equivalent thermal conductivity of each part in motor.
4.2. The Convection Coefficient of Motor
The convection coefficient of different parts in motor is displayed in Table 5.
4.3. One-Way Coupled Field Analysis
The loss brought by cycloidal reducer mechanism is mainly through fiction, the friction loss of motor is small, and the speed of reducer is relatively little. Therefore, the loss generated by reducer is ignored in the thermal calculation. Setting the environment temperature to be 295.13 K, the thermal field of motor at rated state is displayed in Figure 3. It can be found that the temperature of winding is
Table 3. The loss of motor.
Table 4. Thermal conductivity of motor.
Table 5. Convection coefficient of motor (W/(m2・K)).
Figure 3. One-way coupled field at rated speed.
the highest, the second is stator core, and the lowest is rotor. Because the copper loss is the largest, the eddy current loss and core loss in rotor is small, and the convection coefficient of rotor is the maximum of all parts.
When the rotating speed is changing, the one-way coupled field results are shown in Table 6.
Table 6. Temperature of motor at different speed (K).
Table 6 indicates that the temperature increases slowly while the speed raises from 300 rpm to 1200 rpm, the temperature is the lowest when the motor is at rated condition. It may be caused by the decreases of loss and the enhancement of convection.
4.4. Two-Way Interaction Analysis
Taking the influence of temperature change to material property into consideration, the copper is chosen to discuss the difference between this analytic way and the former one. The influence of temperature in the copper is:
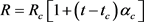 (8)
(8)
where, R is the resistance value when the temperature is t; Rc is the resistance value when the temperature is tc; tc is the initial temperature, it’s set to be 295.13 K; αc is the resistance coefficient when the temperature is tc.
Based on the one-way coupled field, changing the material properties of winding according to formula 8. The two-way interaction analysis is carried out when the motor is rotating at rated speed, the result is shown in Figure 4.
It can be found that the temperature of each part has increased considering the influence of temperature on the resistance value. In the two-way coupled field, the temperature of winding rises 1.8 K, stator rises 0.53 K, rotor and permanent magnet rises 0.2 K. Because the copper loss of winding increases, the rest has no obvious variation at rated condition.
Then Table 7 displays the results of two-way interaction method when the motor rotating speed is changing.
It can be found that the trend of temperature variation in Table 7 is similar to Table 6, but the temperature is bigger in Table 7, caused by the effect of temperature on winding material.
Table 8 shows the highest temperature rising that can be accept by commonly used insulation materials at different grades. The maximum temperature rising of winding is 51.03 K, it’s within the allowed temperature rising range. Meanwhile, the temperature rising of stator, rotor and permanent magnet is also in regular range.
5. Conclusion
A power structure consisting of a cycloidal reducer and a permanent magnet brushless DC motor has been proposed in paper, and this structure is applied in
Table 7. Temperature of motor at different speed (K).
Table 8. Temperature rising grade of insulation.
Figure 4. Two-way interaction analysis at rated speed.
the electric balanced vehicle. The permanent magnet brushless DC motor is chosen as object to analyze and calculate the basic loss. The coupled field analysis method is used to analyze the electromagnetic field and temperature field inside the motor to obtain the motor temperature. The results show that the temperature of motor is in the safety range, won’t do damage to the motor.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Wang, B.G., Li, J.G. and Ai, D. (2019) Temperature Research of Permanent Magnet Brushless DC Motor for Electric Balanced Vehicle. World Journal of Engineering and Technology, 7, 1-9. https://doi.org/10.4236/wjet.2019.74B001
References
- 1. Chen, L.I., Zhu, F., Zhang, M., et al. (2011) Design and Analysis of an Electrical Variable Transmission for a Series-Parallel Hybrid Electric Vehicle. IEEE Transactions on Vehicular Technology, 60, 2354-2363. https://doi.org/10.1109/TVT.2011.2134876
- 2. Rose, G. (2012) E-Bikes and Urban Transportation: Emerging Issues and Unresolved Questions. Transportation, 39, 81-96. https://doi.org/10.1007/s11116-011-9328-y
- 3. Hong, J.H., Huang, C.F., Lu, K.Y., et al. (2013) Analysis and Design of a Passive Steering Mechanism for a Pedaled, Self-Balanced, Personal Mobility Vehicle. IEEE/ SICE International Symposium on System Integration, Sapporo, Japan. https://doi.org/10.1109/SII.2013.6776671
- 4. Nurse, J.A. (1998) Development of Modern High-Voltage Insulation Systems for Large Motors and Generators. Power Engineering Journal, 12, 125-130. https://doi.org/10.1049/pe:19980305
- 5. Li, Y., Xuan, C. and Sun, F. (2010) Study on 3D Thermal Field and Thermal Stress Field of the Induction Motor Rotor. Electric Machines & Control, 77, 571.
- 6. Qian, R.C. (2012) Calculation and Analysis of the 3D Thermal Stress Fields and Stating Performance in Induction Motor With Compound Cage Rotor. Harbin University of Science and Technology, Harbin.
- 7. Yang, Y.P. and Ding, F.X. (2015) Driving-Scenario Oriented Design of an Axial-Flux Permanent-Magnet Synchronous Motor for a Pedal Electric Cycle. IET Electr. Power Appl, 9, 420-428. https://doi.org/10.1049/iet-epa.2014.0351
- 8. Lamme, B.G. (1916) Iron Losses in Direct-Current Machines. Transactions of the American Institute of Electrical Engineers, 35, 261-299. https://doi.org/10.1109/T-AIEE.1916.4765385
- 9. Jing, Z., Cheng, D., Ping, Z., et al. (2012) Field Weakening Capability Investigation of an Axial Flux Permanent-Magnet Synchronous Machine with Radially Sliding Permanent Magnets Used for Electric Vehicles. Journal of Applied Physics, 111, 912. https://doi.org/10.1063/1.3676230






