ABSTRACT

The solution of a nonlinear elliptic equation involving Pucci maximal operator and super linear nonlinearity is studied. Uniqueness results of positive radial solutions in the annulus with Dirichlet boundary condition are obtained. The main tool is Lane-Emden transformation and Koffman type analysis. This is a generalization of the corresponding classical results involving Laplace operator.

1. Introduction

We study the nonlinear elliptic equation

(1)

where is Pucci maximal operator, the potential f is super linear with some further constraints. Using to denote the eigenvalues of then explicitly, the Pucci operator is given by

For more detailed discussion, see for example [1,2]. This equation has been extensively studied, see [3-5], etc. and the references therein.

Normalize to be for simplicity. We will in this paper investigate the uniqueness of positive radial solution of (1) in the annulus

with Dirichlet boundary condition. In this case, Equation (1) reduces to

(2)

where

Throughout the paper, we assume Note that Now we could state our main results.

Theorem 1. Suppose is small enough and

Then (2) has at most one positive solution with Dirichlet boundary condition.

If instead of the smallness of 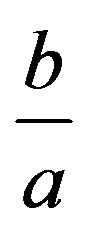we assume further growing condition on then we have the following Theorem 2. Suppose that for,

where

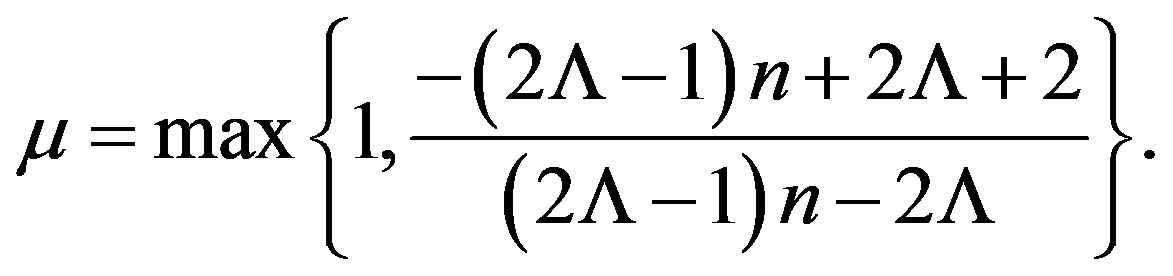
Then (2) has at most one positive solution with Dirichlet boundary condition.

In the case the Pucci operator reduces to the usual Laplace operator, and the corresponding unique results are proved by Ni and Nussbaum in [6].

We also remark that the above theorems could be generalized to nonlinearities which also depends on We will not pursue this further in this paper.

2. Lane-Emden Transformation and Uniqueness of the Radial Solutions

2.1. Proof of Theorem 1

We shall perform a Lane-Emden type transformation to Equation (2). Let us introduce a new function

where with

Then 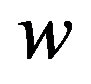satisfies

(3)

where we have denoted

and Note that m may not be continuous at the points where or Additionally, if and then

Lemma 3. Let w be a positive solution of (3) with Then there exists such that and

Proof. If for some then

The conclusion of the lemma follows immediately from this inequality. ■

Given 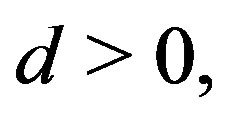the solution of (3) with and will be denoted by. Let

By standard argument, we know that positive solution of (3) with Dirichlet boundary condition is unique if we could show that

whenever is a positive solution to (3) with

The functions and satisfy the following equations:

The initial condition satisfied by is:,.

Now let be a positive constant such that is a positive solution to (3) with. To show that, let us first prove that must vanish at some point in the interval In the following, we write simply as

Lemma 4. There exists such that.

Proof. Let us consider the function

We have

We remark that is indeed not everywhere differentiable, since m is not continuous. It however could be shown that the jump points of m are isolated. Here by, we mean the derivative of at the point where it is differentiable. The same remark applies to the functions and below.

Now if for then

Since we infer that

It follows that

This is a contradiction, since and . ■

With the above lemma at hand, we wish to show that in the interval vanishes at only one point ξ. For this purpose, let us define functions and Put

and

Lemma 5. We have

(4)

(5)

Proof. Differentiate the Equation (3) with respect to s gives us

(6)

Hence

As to the function h, there holds

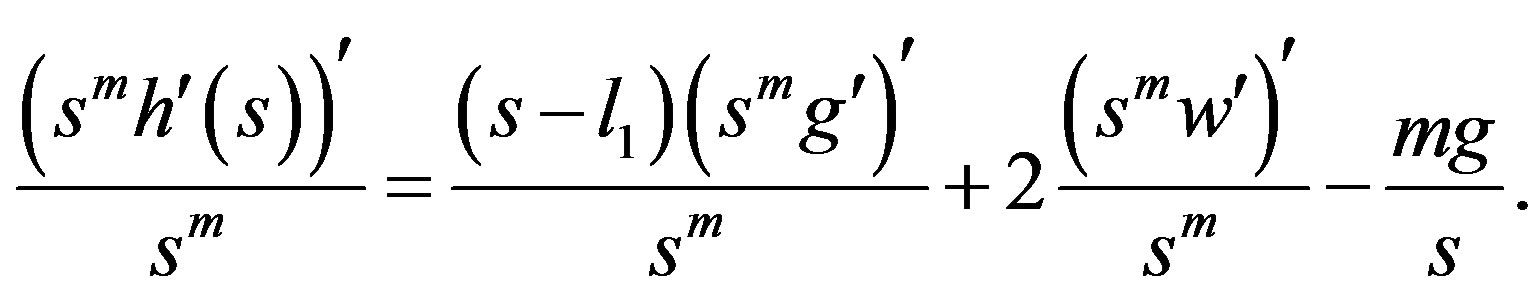
Combining this with (3) and (6) we get

It follows that

■

Now we are ready to prove Theorem 1.

Proof of Theorem 1. We need to show that.

We first of all claim that the first zero of in must stay in the interval where is given by Lemma 3. Suppose to the contrary that

By (5) using the fact that we find that if is small enough, then in the interval

Since we find that

Therefore

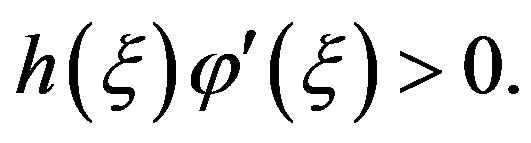
This is a contradiction, since and

Now the first zero of lies in If then the second zero of lies in Note that in Therefore, by identity (4)

This together with

implies that

but this contradicts with, , and This finishes the proof. ■

2.2. Proof of Theorem 2

Similar arguments as that of Theorem 1 could be used to prove Theorem 2. In this case, we shall make the following transform:

where

and 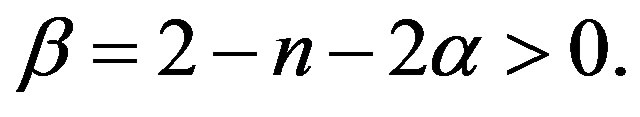Then

(7)

With this transformation, in the interval , w satisfies

(8)

where

By the definition of one could verify that Note that and are step functions and not continous.

Let be the solution of (8) with and. Now similar as in the proof of Theorem 1, we suppose is a positive solution with Dirichlet boundary condition and. We have the following lemma, whose proof will be omitted.

Lemma 6. There exists such that , and

With this lemma at hand, we observe that by (8)

This combined with (7) tells us that Then it is not difficult to show that for and while for

Recall that satisfies

Consider the function then

From this we infer that the function must change sign in the interval similar as that of Theorem 1.

Now let us define

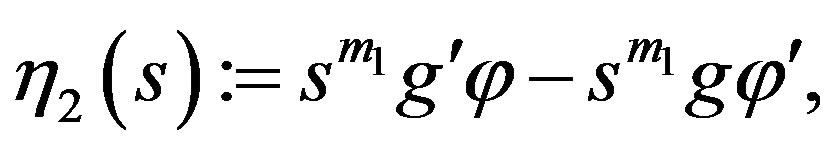
and

where and Moreover, denote

Lemma 7. There holds

Proof. Direct calculation shows

and

This then leads to the desired identity. ■

Now with the help of this lemma, we could prove Theorem 2.

Proof of Theorem 2. First we show the first zero of is in the interval Otherwise, since

one could then use the fact that in and to deduce that in

But this contradicts with 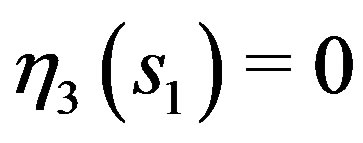and.

Now if the second zero of is in Then since

one could use in to deduce that in 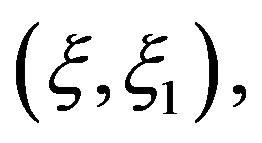which contradicts with and ■

3. Acknowledgements

The author would like to thank Prof. P. Felmer for useful discussion.

REFERENCES

NOTES

^*The author is supported by NSFC under grant 11101141; SRF for ROCS, SEM; DF of NCEPU.