ABSTRACT

This research work considers the following inequalities: $\lambda A\left(a\mathrm{,}b\right)+\left(1-\lambda \right)C\left(a\mathrm{,}b\right)\le \bar{C}\left(a\mathrm{,}b\right)\le \mu A\left(a\mathrm{,}b\right)+\left(1-\mu \right)C\left(a\mathrm{,}b\right)$ and $C\left[\lambda a+\left(1-\lambda \right)b\mathrm{,}\lambda b+\left(1-\lambda \right)a\right]\le \bar{C}\left(a\mathrm{,}b\right)\le C\left[\mu a+\left(1-\mu \right)b\mathrm{,}\mu b+\left(1-\mu \right)a\right]$ with $A\left(a,b\right)=\frac{a+b}{2}$ ; $C\left(a,b\right)=\frac{a^2+b^2}{a+b}$,$\bar{C}\left(a\mathrm{,}b\right)=\frac{2\left(a^2+ab+b^2\right)}{3\left(a+b\right)}$. The researchers attempt to find an answer as to what are the best possible parameters $\lambda \mathrm{,}\mu$ that (1.1) and (1.2) can be hold? The main tool is the optimization of some suitable functions that we seek to find out. By searching the best possible parameters such that (1.1) and (1.2) can be held. Firstly, we insert $f\left(t\right)=\lambda A\left(a\mathrm{,}b\right)+\left(1-\lambda \right)C\left(a\mathrm{,}b\right)-\bar{C}\left(a\mathrm{,}b\right)$ without the loss of generality. We assume that $a>b$ and let $t=\frac{a}{b}>1$ to determine the condition for $\lambda$ and $\mu$ to become $f\left(t\right)\le 0$. Secondly, we insert $g\left(t\right)=\mu A\left(a\mathrm{,}b\right)+\left(1-\mu \right)C\left(a\mathrm{,}b\right)-\bar{C}\left(a\mathrm{,}b\right)$ without the loss of generality. We assume that $a>b$ and let $t=\frac{a}{b}>1$ to determine the condition for $\lambda$ and $\mu$ to become $g\left(t\right)\ge 0$.

Keywords:

Centroidal Mean, Arithmetic Mean, Contraharmonic Mean

1. Introduction

For $a,b>0$ with $a\ne b$, the Centroidal mean $\bar{C}\left(a\mathrm{,}b\right)$, Harmonic mean $A\left(a\mathrm{,}b\right)$ and Contraharmonic mean $C\left(a\mathrm{,}b\right)$ are defined by:

$\bar{C}\left(a,b\right)=\frac{2\left(a^2+ab+b^2\right)}{3\left(a+b\right)},A\left(a,b\right)=\frac{a+b}{2};C\left(a,b\right)=\frac{a^2+b^2}{a+b}$

respectively.

The main objective of this research work is to present optimization of the following inequalities:

$\lambda A\left(a\mathrm{,}b\right)+\left(1-\lambda \right)C\left(a\mathrm{,}b\right)\le \bar{C}\left(a\mathrm{,}b\right)\le \mu A\left(a\mathrm{,}b\right)+\left(1-\mu \right)C\left(a\mathrm{,}b\right)$ (1.1)

and

$C\left[\lambda a+\left(1-\lambda \right)b\mathrm{,}\lambda b+\left(1-\lambda \right)a\right]\le \bar{C}\left(a\mathrm{,}b\right)\le C\left[\mu a+\left(1-\mu \right)b\mathrm{,}\mu b+\left(1-\mu \right)a\right]$ (1.2)

Recently, both mean values have been the subject of intensive research. In particular, many remarkable inequalities and properties for these means can be found in the literature [1] [2].

This work finds out such inequality that arises in the search for determination of a point of reference about which some function of variants would be minimum or maximum. Since very early times, people have been interested in the problem of choosing the best single quantity, which could summarize the whole information contained in a number of observations (measurements). Moreover, the theory of means has its roots in the work of the Pythagorean who introduced the harmonic, geometric, and arithmetic means. Peter et al. [3] introduced seven other means and gave the well-known elegant geometric proof of the celebrated inequalities among the harmonic, geometric, and arithmetic means. The strong relations and introduction of the theory of means with the theories of inequalities, function equations, probability and statistics add greatly to its importance. This single element is usually called a means or average. The term “means” or “average” (middle value) has for a long time been used in all branches of human activity.

The basic function of mean value is to represent a given set of many values by some single value. In [4], the authors were the first time introduced power means defined the meaning of the term “representation” as determination of appoint of reference about which some function of variants would be minimum. More recently the means were the subject of research and study whereas essential areas in several applications such as: physics, economics, electrostatics, heat conduction, medicine and even in meteorology. It can be observed that the power mean $M_p\left(a\mathrm{,}b\right)$ of order p can be rewritten as (see as [5])

$M_p\left(a,b\right)=\{\begin{array}{l}{\left({\frac{a^p+b}{2}}^p\right)}^{\frac{1}{p}};p\ne 0\\ \sqrt{ab};p=0\end{array}$

If we denote by

$A\left(a\mathrm{,}b\right)=\frac{1}{2}\left(a+b\right)\mathrm{,}G\left(a\mathrm{,}b\right)=\sqrt{ab}\text{and}H\left(a\mathrm{,}b\right)=\frac{2ab}{a+b}\mathrm{,}$

the arithmetic, geometric and harmonic means of two positive numbers a and b, respectively. In addition, the logarithmic and identric means of two positive real numbers a and b defined by [6]

$L\left(a\mathrm{,}b\right)\mathrm{<mo>\; =\; </mo>}\{\begin{array}{l}\frac{b-a}{\log b-\log a}a\ne b\\ aa=b\end{array}$

$I\left(a\mathrm{,}b\right)=\{\begin{array}{l}\frac{1}{e}{\left(\frac{b^b}{a^a}\right)}^{1/\left(b-a\right)}a\ne b\\ aa=b\end{array}$

Several authors investigated and developed relationship of optimal inequalities between the various means.

The well-known inequality that:

$\begin{array}{l}\min \left\{a,b\right\}\le H\left(a,b\right)=M_{-1}\left(a,b\right)\le G\left(a,b\right)=M_0\left(a,b\right)\\ \le L\left(a,b\right)\le I\left(a,b\right)\le A\left(a,b\right)=M_1\left(a,b\right)\le \max \left\{a,b\right\}\end{array}$

and all inequalities are strict for $a\ne b$.

In [7], researchers studied what are the best possible parameters ${\alpha }_1\mathrm{,}{\alpha }_2\mathrm{,}{\beta }_1$ and ${\beta }_2$ by two theorems:

Theorem (1) the double inequality: -

${\alpha }_{1}A\left(a\mathrm{,}b\right)+\left(1-{\alpha }_1\right)H\left(a\mathrm{,}b\right)\le L\mathrm{<mo\; stretchy="false">(\; </mo>}a\mathrm{,}b\mathrm{<mo\; stretchy="false">)\; </mo>}\le {\beta }_{1}A\left(a\mathrm{,}b\right)+\left(1-{\beta }_1\right)H\left(a\mathrm{,}b\right)$

holds for all $a,b>0$ if and only if ${\alpha }_1\le 0$ and ${\beta }_1\ge \frac{2}{3}$ when proved that the parameters ${\alpha }_1\le 0$ and ${\beta }_1\ge \frac{2}{3}$ cannot be improved.

Theorem (2) the double inequality: -

${\alpha }_{2}A\left(a\mathrm{,}b\right)+\left(1-{\alpha }_2\right)H\left(a\mathrm{,}b\right)\le L\left(a\mathrm{,}b\right)\le {\beta }_{2}A\left(a\mathrm{,}b\right)+\left(1-{\beta }_2\right)H\left(a\mathrm{,}b\right)$

holds for all $a,b>0$ if and only if ${\alpha }_2\le \frac{2}{e}$ and ${\beta }_2\ge \frac{5}{6}$ when proved that the parameters ${\alpha }_2\le \frac{2}{e}$ and ${\beta }_2\ge \frac{5}{6}$ cannot be improved.

Interestingly in [5] B. Long et al., proved that the following results: $M_0\left(a\mathrm{,}b\right)$ and $M_{tl3}\left(a\mathrm{,}b\right)$ are the best possible lower and upper power bounds for the generalized logarithmic mean $L_t\left(a\mathrm{,}b\right)$ for any fixed $t>0$ the double inequalities

$M_0\left(a,b\right)<L_t\left(a,b\right)<M_{tl3}\left(a,b\right)$

holds for all $a,b>0$ with $a\ne b$, and they found $L_2\left(a\mathrm{,}b\right)$ the optimal lower generalized logarithmic means bound for the identric means $I\left(a\mathrm{,}b\right)$ for inequalities $L_2\left(a,b\right)<I\left(a,b\right)$ holds for all a, b are positive numbers with $a\ne b$. Pursuing another line of investigation, in [8] the authors showed the sharp upper and lower bounds for the Neuman-sandor $NS\left(a\mathrm{,}b\right)$. [9] in terms of the liner convex combination of the logarithmic means $L\left(a\mathrm{,}b\right)$, and second seiffert means $T\left(a\mathrm{,}b\right)$ [10] of two positive numbers a and b, respectively for the double inequalities

$\alpha L\left(a\mathrm{,}b\right)+\left(1-\alpha \right)T\left(a\mathrm{,}b\right)\le NS\left(a\mathrm{,}b\right)\le \beta L\left(a\mathrm{,}b\right)+\left(1-\beta \right)T\left(a\mathrm{,}b\right)$

holds for all $a,b>0$ with $a\ne b$ is true if and only if $\alpha \ge \frac{1}{4}$ and $\beta \le 1-\pi l\left[4\log \left(1+\sqrt{2}\right)\right]$.

In [11] have improvements and refinements by HZ Xu et al., for they found several sharp upper and lower bounds for the Sandor-yang means $R_{QA}\left(a\mathrm{,}b\right)$ and $R_{AQ}\left(a\mathrm{,}b\right)$. [12] [13] in terms of combinations of the arithmetic means $A\left(a\mathrm{,}b\right)$ and the contra-harmonic mean $C\left(a\mathrm{,}b\right)$. [4] [14].

The authors have to proven our main results several lemmas find the best possible parameters ${\alpha }_i,{\beta }_i/\left(i=1,2,3,4\right)$ such that the double inequalities

$c^{{\alpha }_1}\left(a,b\right)A^{1-{\alpha }_1}\left(a,b\right)<R_{QA}\left(a,b\right)<c^{{\beta }_1}\left(a,b\right)A^{1-{\beta }_1}\left(a,b\right)$

$c^{{\alpha }_2}\left(a,b\right)A^{1-{\alpha }_2}\left(a,b\right)<R_{QA}\left(a,b\right)<c^{{\beta }_2}\left(a,b\right)A^{1-{\beta }_2}\left(a,b\right)$

$\begin{array}{l}{\alpha }_3\left[\frac{1}{3}C\left(a,b\right)+\frac{2}{3}A\left(a,b\right)\right]+\left(1-{\alpha }_3\right)C^{1/3}\left(a,b\right)A^{2/3}\left(a,b\right)\\ <R_{QA}\left(a,b\right)<{\beta }_3\left[\frac{1}{3}C\left(a,b\right)+\frac{2}{3}A\left(a,b\right)\right]+\left(1-{\beta }_3\right)C^{1/3}\left(a,b\right)A^{2/3}\left(a,b\right),\end{array}$

$\begin{array}{l}{\alpha }_4\left[\frac{1}{6}C\left(a,b\right)+\frac{5}{6}A\left(a,b\right)\right]+\left(1-{\alpha }_4\right)C^{1/6}\left(a,b\right)A^{5/6}\left(a,b\right)\\ <R_{AQ}\left(a,b\right)<{\beta }_4\left[\frac{1}{6}C\left(a,b\right)+\frac{5}{6}A\left(a,b\right)\right]+\left(1-{\beta }_4\right)C^{1/6}\left(a,b\right)A^{5/6}\left(a,b\right)\end{array}$

holds for all $a,b>0$ with $a\ne b$.

In [15], Neuman proved that the double inequalities

$\lambda C\left(a,b\right)+\left(1-\lambda \right)A\left(a,b\right)\le M\left(a,b\right)\le \mu C\left(a,b\right)+\left(1-\mu \right)A\left(a,b\right),$

with $M\left(a,b\right)$ is the Neuman-S andor mean, hold for all holds for all $a,b>0$ with $a\ne b$ if and only if $\lambda \le \frac{1-\log \left(1+\sqrt{2}\right)}{\log \left(1+\sqrt{2}\right)}$ and $\mu \ge \frac{1}{6}$. In [2] Shen, the inequalities sharps bounds for Seiffert mean in terms of Contraharmonic mean

$C\left[\lambda a+\left(1-\lambda \right)b\mathrm{,}\lambda b+\left(1-\lambda \right)a\right]\le T\left(a\mathrm{,}b\right)\le C\left[\mu a+\left(1-\mu \right)b\mathrm{,}\mu b+\left(1-\mu \right)a\right]\mathrm{,}$

with $T\left(a\mathrm{,}b\right)=\frac{a-b}{2\arctan \left(\frac{a-b}{a+b}\right)}$, were proved to be valid for $\frac{1}{2}<\lambda ,\mu <1$ and for all $a,b<0$ with $a\ne b$ if and only if $\lambda \le \left(1+\sqrt{\frac{4-\pi }{\pi }}\right)$ and $\mu \ge \frac{3+\sqrt{3}}{6}$. Wen-Hui Li and Feng Qi [16], proved that the double inequality

$\lambda Q\left(a\mathrm{,}b\right)+\left(1-\lambda \right)M\left(a\mathrm{,}b\right)\le \bar{C}\left(a\mathrm{,}b\right)\le \mu Q\left(a\mathrm{,}b\right)+\left(1-\mu \right)M\left(a\mathrm{,}b\right)\mathrm{,}$

with $Q\left(a\mathrm{,}b\right)=\sqrt{\frac{a^2+b^2}{2}}$ is the root-square mean, holds for all $a,b>0$ with $a\ne b$ if and only if $\lambda \le \frac{1}{2}$ and $\mu \ge \frac{3-4\ln \left(1+\sqrt{2}\right)}{3\left[1-\sqrt{2}\ln \left(1+\sqrt{2}\right)\right]}=0.7107\cdots$.

For mor information on this topic, you can refer to the following references: [17] [18] [19].

2. Main Results

Motivating by results mentioned above, we naturally ask a question: what are the best possible parameters $\lambda \mathrm{,}\mu$ that (1.1) and (1.2) can be hold?

The aim of this paper is to answer this question. The solution to this question may be stated as the following Theorem:

Theorem 1. Assuming $a>0,b>0$ with $\frac{a}{b}>1$ then,

1) if $\lambda \in \left(\frac{2}{3}\mathrm{,}+\infty \right)$ and $\mu \in \left(-\infty \mathrm{,}\frac{2}{3}\right)$ then, the double inequality (1.1) holds.

2) if $\lambda \in \left(\frac{3-\sqrt{3}}{6}\mathrm{,}\frac{3+\sqrt{3}}{6}\right)$ and $\mu \in \left(-\infty \mathrm{,}-6\right]\cup \left[\mathrm{0,}\frac{3-\sqrt{3}}{6}\right)\cup \left(\frac{3+\sqrt{3}}{6}\mathrm{,}+\infty \right)$ then the double inequality (1.2) holds.

Proof. 1): Assuming $a>0,b>0$ with $\frac{a}{b}>1$

$\lambda \left(\frac{a+b}{2}\right)+\left(1-\lambda \right)\left(\frac{a^2+b^2}{a+b}\right)\le \frac{2\left(a^2+ab+b^2\right)}{3\left(a+b\right)}\le \mu \left(\frac{a+b}{2}\right)+\left(1-\mu \right)\left(\frac{a^2+b^2}{a+b}\right)$

Set $t=\frac{a}{b}>1$. Then, we obtain

$\begin{array}{l}\lambda \left(\frac{b\left(t+1\right)}{2}\right)+\left(1-\lambda \right)\left(\frac{b\left(t^2+1\right)}{t+1}\right)\\ \le \frac{2b\left(t^2+t+1\right)}{3\left(t+1\right)}\le \mu \left(\frac{b\left(t+1\right)}{2}\right)+\left(1-\mu \right)\left(\frac{b\left(t^2+1\right)}{t+1}\right)\end{array}$

We start by showing that

$\lambda \left(\frac{b\left(t+1\right)}{2}\right)+\left(1-\lambda \right)\left(\frac{b\left(t^2+1\right)}{t+1}\right)-\frac{2b\left(t^2+t+1\right)}{3\left(t+1\right)}\le \mathrm{0,}$

$\iff \lambda \frac{3b{\left(t+1\right)}^2}{6\left(t+1\right)}+\left(1-\lambda \right)\frac{6b\left(t^2+1\right)}{6\left(t+1\right)}-\frac{4b\left(t^2+t+1\right)}{6\left(t+1\right)}\le 0$

Because $t>0$ therefore the study amounts to proving that

$\lambda 3b{\left(t+1\right)}^2+\left(1-\lambda \right)6b\left(t^2+1\right)-4b\left(t^2+t+1\right)\le 0.$

Let

$f\left(t\right)=3\lambda b{\left(t+1\right)}^2+6\left(1-\lambda \right)b\left(t^2+1\right)-4b\left(t^2+t+1\right)$

We have to prove that the function f is negative under certain conditions on the parameter $\lambda$, a.e: $f\left(t\right)\le 0$. So

$f\left(t\right)=3\lambda b{\left(t+1\right)}^2+6\left(1-\lambda \right)b\left(t^2+1\right)-4b\left(t^2+t+1\right)\le 0$

Because $f\left(1\right)=0$, it will suffice to show that f is decreasing for all $t>1$, which amounts to studying the sign of the derivative $f^{\prime }$ of f. We have:

$f^{\prime }\left(t\right)=6\lambda b\left(t+1\right)+12\left(1-\lambda \right)bt-4b\left(2t+1\right)$

Because $f^{\prime }\left(1\right)=0$, it will suffice to show that $f^{\prime }$ is decreasing for all $t>1$, which amounts to studying the sign of the derivative $f^{″}$ of $f^{\prime }$. We have:

$f^{″}\left(t\right)=2b\left(2-3\lambda \right)<0\iff \lambda >\frac{2}{3}$

so that $f^{\prime }$ is decreasing for $t>1$ and therefore, we obtain that $f\left(t\right)<0$ because $f\left(1\right)=0$.

Finally in this part for $a>0,b>0$ with $\frac{a}{b}>1$, we obtain that

$\lambda \left(\frac{b\left(t+1\right)}{2}\right)+\left(1-\lambda \right)\left(\frac{b\left(t^2+1\right)}{t+1}\right)\le \frac{2b\left(t^2+t+1\right)}{3\left(t+1\right)},\text{for}\text{all}\lambda >\frac{2}{3}.$

To show the second inequality in this first case, we proceed by similar calculations. This is done by considering the function g defined by

$g\left(t\right)=g\left(t\right)=3\mu b{\left(t+1\right)}^2+6\left(1-\mu \right)b\left(t^2+1\right)-4b\left(t^2+t+1\right).$

So, after all the calculations, we get that for $a>0,b>0$ with $\frac{a}{b}>1$, that $g\left(t\right)\ge 0$, for all $\mu <\frac{2}{3}$. a.e:

$\frac{2\left(a^2+ab+b^2\right)}{3\left(a+b\right)}\le \mu \left(\frac{a+b}{2}\right)+\left(1-\mu \right)\left(\frac{a^2+b^2}{a+b}\right)$

2): Assuming $a>0,b>0$ with $\frac{a}{b}>1$ and with similar calculations and by the same idea we obtain that for all

$\lambda \in \left(\frac{3-\sqrt{3}}{6}\mathrm{,}\frac{3+\sqrt{3}}{6}\right)\text{and}\mu \in \left(-\infty \mathrm{,}-6\right]\cup \left[\mathrm{0,}\frac{3-\sqrt{3}}{6}\right)\cup \left(\frac{3+\sqrt{3}}{6}\mathrm{,}+\infty \right)$

then the double inequality

$C\left[\lambda a+\left(1-\lambda \right)b\mathrm{,}\lambda b+\left(1-\lambda \right)a\right]\le \bar{C}\left(a\mathrm{,}b\right)\le C\left[\mu a+\left(1-\mu \right)b\mathrm{,}\mu b+\left(1-\mu \right)a\right]\mathrm{,}$

holds.

Conclusion 1. In our work, we studied the following double inequalities: respectively (1.1) and (1.2)

$\lambda A\left(a\mathrm{,}b\right)+\left(1-\lambda \right)C\left(a\mathrm{,}b\right)\le \bar{C}\left(a\mathrm{,}b\right)\le \mu A\left(a\mathrm{,}b\right)+\left(1-\mu \right)C\left(a\mathrm{,}b\right)$

and

$C\left[\lambda a+\left(1-\lambda \right)b\mathrm{,}\lambda b+\left(1-\lambda \right)a\right]\le \bar{C}\left(a\mathrm{,}b\right)\le C\left[\mu a+\left(1-\mu \right)b\mathrm{,}\mu b+\left(1-\mu \right)a\right]$

by searching the best possible parameters such that (1.1) and (1.2) can be hold.

Firstly, we have inserted

$f\left(t\right)=\lambda A\left(a,b\right)+\left(1-\lambda \right)C\left(a,b\right)-\bar{C}\left(a,b\right)$

and

$g\left(t\right)=\mu A\left(a,b\right)+\left(1-\mu \right)C\left(a,b\right)-\bar{C}\left(a,b\right)$

Without loss of generality, we have assumed that $a>b$ and let $t=\frac{a}{b}>1$ to determine the condition for $\lambda$ and $\mu$ to become $f\left(t\right)\le 0$ and $g\left(t\right)\ge 0$.

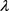Secondly, we have inserted Without loss of generality, we assume that $a>b$ and let to determine the condition for and 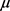to become

And finally, we got that:

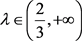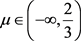1) if and then, the double inequality (1.1) holds.

2) if 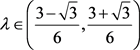and then the double inequality (1.2) holds.

Acknowledgements

The authors gratefully acknowledge Qassim University, represented by the Deanship of Scientific Research, on the material support for this research WORK under the number (1063) during the academic year 1441AH/2020AD.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

Cite this paper

El Mokhtar Ould El Mokhtar, M. and Alharbi, H. (2020) On Two Double Inequalities (Optimal Bounds and Sharps Bounds) for Centroidal Mean in Terms of Contraharmonic and Arithmetic Means. Journal of Applied Mathematics and Physics, 8, 1039-1046. https://doi.org/10.4236/jamp.2020.86081

References