Optics and Photonics Journal
Vol.2 No.2(2012), Article ID:20404,6 pages DOI:10.4236/opj.2012.22017
Stability of Nonlinear Te Surface Waves along the Boundary of Left-Handed Material
Physics Department, Al Azhar University, Gaza, Palestinian Authority
Email: H.Mousa@alazhar-gaza.edu
Received March 30, 2012; revised April 28, 2012; accepted May 7, 2012
Keywords: Nonlinear Waves; Wave-Guides; Dispersion Relation; Left-Handed Material; Growth Rate; Stability
ABSTRACT
This paper is concerned with the stability characteristics of nonlinear surface waves propagating along a left-handed substrate (LHM) and a non-linear dielectric cover. These characteristics have been simulated numerically by using the perturbation method. The growth rate of perturbation is computed by solving the dispersion equation of perturbation. I found that the stability of nonlinear surface waves is affected by the frequency dependence of the electric permittivity εh and magnetic permeability μh of the LHM. The spatial evolution of the steady state field amplitude is determined by using computer simulation method. The calculations show that with increasing the effective refractive index nx at fixed saturation parameter μp, the field distribution is sharpened and concentrated in the nonlinear medium. The waves are stable of forward and backward behavior. At higher values of nx, attenuated backward waves are observed.
1. Introduction
Recently, there has been great interest in new type of electromagnetic materials called left-handed media [1]. Over fifty years ago, Veselago was the first to consider the left-handed meta-material (LHM) which he defined as media with simultaneously negative and almost real electric permittivity and magnetic permeability in some frequency range [2]. The electric and magnetic fields form a left-handed set of vectors with the wave vector [3]. These materials have been shown to exhibit unique properties, such as Snell law and Doppler shift. Smith, et al. [4] have built these materials by using two dimensional arrays of splitting resonators and wires and are operating the microwave range. Nonlinear surface waves propagating along the interface of linear and nonlinear media have a number of novel extraordinary properties which attracted attention of many investigators [5-8]. Understanding the stability of nonlinear surface waves is essential for the exploitation of these waves in various devices. There are numbers of approaches to the problem both using numerical simulations methods by Akhmediev et al. [8] and Moloney et al. [5] and analytical methods by Tran [6] which has been based on steady-state solutions to a nonlinear wave equation which contains an intensity dependent refractive index. The question is whether these wave solutions are stable on propagation of waves. Akhmediev et al. [8] had shown when the growth rate of perturbation of waves  is real, the surface waves are unstable and when
is real, the surface waves are unstable and when 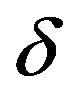 is imaginary, the waves are stable. Akhmediev et al. [7] explained the stability behavior of antisymmetric and symmetric solutions of a linear core sandwiched between two nonlinear media. They showed that the antisymmetric wave is stable at high values of the propagation constant, in contrast to the symmetric wave. Hasegawa [9] studied the soliton effects in various fibers, he reported that, optical soliton is formed by a balance between the dispersion velocity of the waves and the Kerr nonlinearity of the fiber. Sukhorukov et al. investigated the Spatial optical solitons in waveguide arrays, they predicted, two-dimensional (2D) networks of nonlinear waveguides which allow a possibility of realizing useful functional operations with discrete solitons such as signal switching, blocking, routing, and time gating [10,11]. Setzpfandt et al. described discrete solitons in quadratic waveguide arrays [12]. Their results demonstrated that a power threshold may appear for soliton formation, leading to a suppression of beam self-focusing which explains recent experimental observations. Shabat and Mousa have studied the stability of nonlinear surface waves along the boundary of linear semiconductor [13] and along the boundary of lateral antiferromagnetic/nonmagnetic superlattice (LANS) [14]. These studies were carried out in a media with positive refractive index. Such media are called right handed materials.
is imaginary, the waves are stable. Akhmediev et al. [7] explained the stability behavior of antisymmetric and symmetric solutions of a linear core sandwiched between two nonlinear media. They showed that the antisymmetric wave is stable at high values of the propagation constant, in contrast to the symmetric wave. Hasegawa [9] studied the soliton effects in various fibers, he reported that, optical soliton is formed by a balance between the dispersion velocity of the waves and the Kerr nonlinearity of the fiber. Sukhorukov et al. investigated the Spatial optical solitons in waveguide arrays, they predicted, two-dimensional (2D) networks of nonlinear waveguides which allow a possibility of realizing useful functional operations with discrete solitons such as signal switching, blocking, routing, and time gating [10,11]. Setzpfandt et al. described discrete solitons in quadratic waveguide arrays [12]. Their results demonstrated that a power threshold may appear for soliton formation, leading to a suppression of beam self-focusing which explains recent experimental observations. Shabat and Mousa have studied the stability of nonlinear surface waves along the boundary of linear semiconductor [13] and along the boundary of lateral antiferromagnetic/nonmagnetic superlattice (LANS) [14]. These studies were carried out in a media with positive refractive index. Such media are called right handed materials.
This paper is concerned with the stability of nonlinear surface waves propagating along the boundary of lefthanded media [1] (LHM).
To study the stability of the corresponding surface waves, it is necessary to select a particular form of the frequency dependence of the electric permittivity  and magnetic permeability
and magnetic permeability 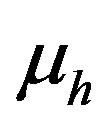 of the LHM, I solve this problem by using computer simulation method [15].
of the LHM, I solve this problem by using computer simulation method [15].
The geometry is shown in Figure 1. It consists of a non-linear semi-infinite cladding contact everywhere to a linear, semi-infinite LHM substrate at  planar interface. The coordinate system is such that, the y axis is normal to the interface and the wave vector is directed along the
planar interface. The coordinate system is such that, the y axis is normal to the interface and the wave vector is directed along the  axis.
axis.
2. Theoretical Analysis
Since the wave propagation is in x-direction then, the Maxwell equations for S-polarized wave (TE) are reduced to the following Equation [8]
 (1)
(1)
The dielectric constant of the linear medium in the region  is
is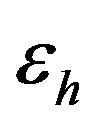 , while the dielectric function in region
, while the dielectric function in region  is:
is:
 (2)
(2)
Assuming that the nonlinear medium is self-focusing, the solution of the wave equation which is polarized along the z-axis is:
 (3)
(3)
where  is a slowly varying field envelope,
is a slowly varying field envelope,  is the effective refractive index.
is the effective refractive index.
By substituting Equation (3) into Equation (1), the equation for the slowly varying amplitude  is then [5]
is then [5]
 (4a)
(4a)
where
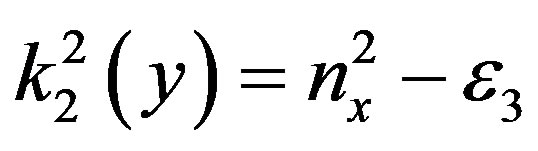 (4b)
(4b)

Figure 1. Configuration of a single interface nonlinear cover/LHM substrate structure.
is the decay constant of the nonlinear medium,  is the linear part dielectric function of the non linear medium, the coordinates
is the linear part dielectric function of the non linear medium, the coordinates  and
and  are normalized by the factor
are normalized by the factor , and the fields are normalized by the factor
, and the fields are normalized by the factor , where
, where 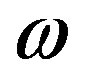 is the wave angular frequency,
is the wave angular frequency,  is the light velocity in free space, and
is the light velocity in free space, and  is the non-linearity coefficient.
is the non-linearity coefficient.
The investigation of the stability of nonlinear surface wave (NSW) propagation along the interface between the linear and non linear medium has been focused in looking for the steady-state solution  of Equation (4a) in the proposed structure as:
of Equation (4a) in the proposed structure as:
 (5)
(5)
At the interface between the two media , we assume the condition that the dielectric constant of the linear medium
, we assume the condition that the dielectric constant of the linear medium  and
and
 (6a)
(6a)
where
 (6b)
(6b)
is the decay constant of the linear medium.
Both a negative dielectric permittivity and permeability are written as [3]:
|
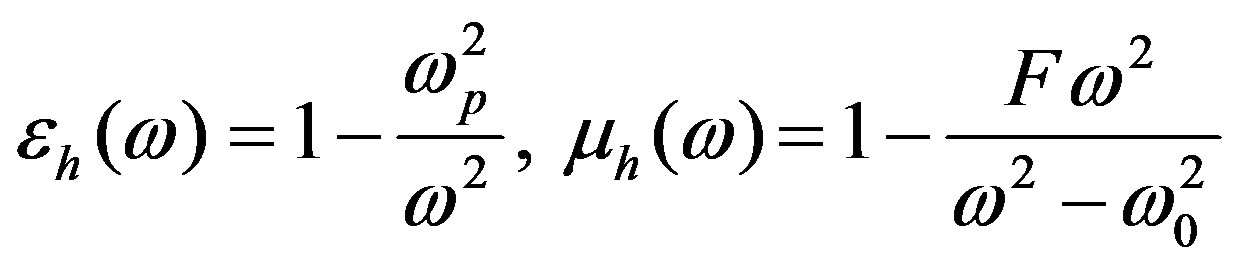 (6c) with plasma frequency
(6c) with plasma frequency  and resonance frequency
and resonance frequency .
.To determine the stability criterion for NSWs, I numerically stimulated the steady-state solution of Equation (4a) with small perturbation as [8]:
 (7)
(7)
where 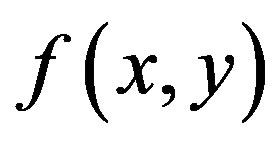 is a perturbation function of the steady-state solution,
is a perturbation function of the steady-state solution,  is the saturation parameter.
is the saturation parameter.
Substituting Equation (7) into Equation (4a), we can obtain:
 (8)
(8)
We shall consider the  dependence of the perturbation function, so that the function can be written in the form [8]:
dependence of the perturbation function, so that the function can be written in the form [8]:
 (9)
(9)
where 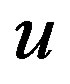 and
and  are functions of
are functions of  only. We take the case
only. We take the case  for nonlinear medium.
for nonlinear medium.
Substituting Equation (9) into Equation (8), we obtain the set of differential equations which have solutions decay as  for self focused waves in nonlinear medium of the form:
for self focused waves in nonlinear medium of the form:
 (10)
(10)
where
 where
where 
 are constants to be determined from the boundary condition, and primes denote the derivatives with respect to
are constants to be determined from the boundary condition, and primes denote the derivatives with respect to .
.
In a linear medium, the solutions are decaying as ,
,
 (11)
(11)
where  and
and  are constants to be determined from the boundary conditions. For a surface wave
are constants to be determined from the boundary conditions. For a surface wave  is either real or imaginary, thus by a bit of algebra we can obtain a dispersion relation for determining
is either real or imaginary, thus by a bit of algebra we can obtain a dispersion relation for determining  of the form [8]:
of the form [8]:
 (12a)
(12a)
where  which implies
which implies  and
and
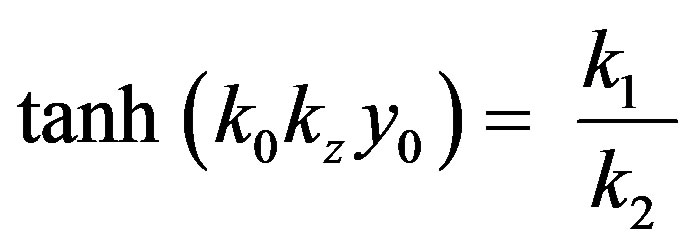 (12b)
(12b)
Equation (12a) may be solved analytically by expanding each of the two expressions under the absolute value in terms of  up to the fourth order and by calculating the absolute values of these expressions, one obtains that [8]
up to the fourth order and by calculating the absolute values of these expressions, one obtains that [8]
 (13)
(13)
when  is real, the growth rate
is real, the growth rate  is related to
is related to 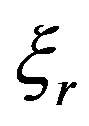 by Reference [8],
by Reference [8], 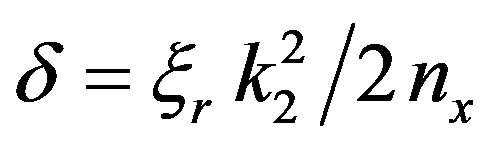 which causes the NSW to be unstable.
which causes the NSW to be unstable.
When  is imaginary where
is imaginary where  becomes imaginary and NSW is stable. At
becomes imaginary and NSW is stable. At ,
,  is the critical refractive index in this case.
is the critical refractive index in this case.
The evolution of the perturbed field amplitude  at the propagation distance
at the propagation distance  is calculated by the determination of the constants
is calculated by the determination of the constants  through application of the boundary conditions at y = 0 as [5]:
through application of the boundary conditions at y = 0 as [5]:
(1) (14)
(14)
It is found by substituting Equations (5) & (7) into Equation (3), which results in
(2)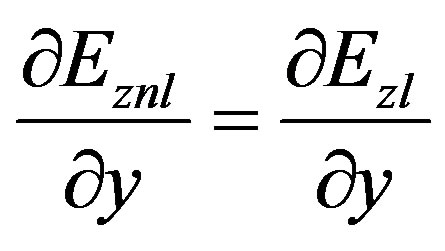 (15a)
(15a)
Since the wave function u vanishes at the boundary, say y =10 then (3) 
(4) (15b)
(15b)
At the initial perturbation where , it is convenient to take
, it is convenient to take , then by solving the two Equations (14) and (15), we can obtain the values of the constants
, then by solving the two Equations (14) and (15), we can obtain the values of the constants . By numerical simulation method it is easy to study the evolution of the steady-state field amplitude
. By numerical simulation method it is easy to study the evolution of the steady-state field amplitude
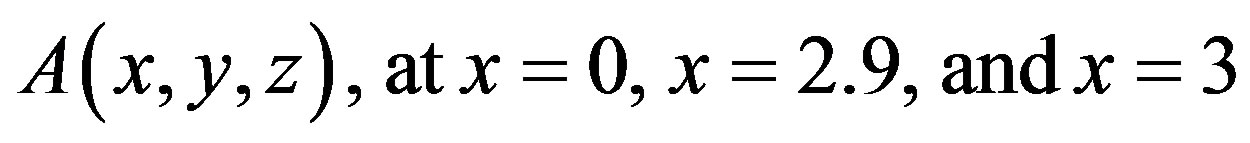 .
.
The variation of the energy integral of the nonlinear surface waves with  is also calculated analytically for different values of the wave frequency through the integral of square perturbed field amplitude in linear and nonlinear medium as [8]
is also calculated analytically for different values of the wave frequency through the integral of square perturbed field amplitude in linear and nonlinear medium as [8]
 (16)
(16)
where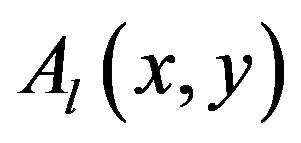 ,
,  are the perturbed field amplitude in linear and nonlinear medium respectively.
are the perturbed field amplitude in linear and nonlinear medium respectively.
3. Computer Simulation and Discussion
Some numerical calculations are presented for the simulation of the stability Equation (7) of the proposed structure, which consists of LHM substrate and a nonlinear dielectric cover. Computer simulation software (Maple) [15] is used in our computation, where the run takes a reasonable usage time. The parameters are [3] as follows: , and
, and 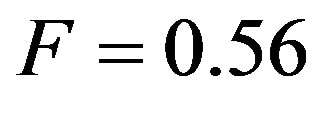 and for the non-linear medium,
and for the non-linear medium, . Figures 2(a)-(c) show that for this set of parameters, the frequency range in which both
. Figures 2(a)-(c) show that for this set of parameters, the frequency range in which both and
and are negative is from 4 GHz to 6 GHz.
are negative is from 4 GHz to 6 GHz.
For increasing values of wave frequency ( ), Figures 2(a)-(c) display the spatial evolution of steady state field amplitude
), Figures 2(a)-(c) display the spatial evolution of steady state field amplitude ,
,  as a function of the wave frequency (
as a function of the wave frequency (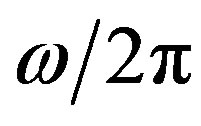 ). I found that at
). I found that at  and wave frequency (
and wave frequency (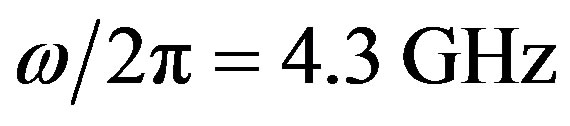 ), (
), ( ) are of values (–4.4, –3.185) respectively as computed from Equation (6c). The perturbed waves are unstable where the growth
) are of values (–4.4, –3.185) respectively as computed from Equation (6c). The perturbed waves are unstable where the growth
 (a)
(a) (b)
(b)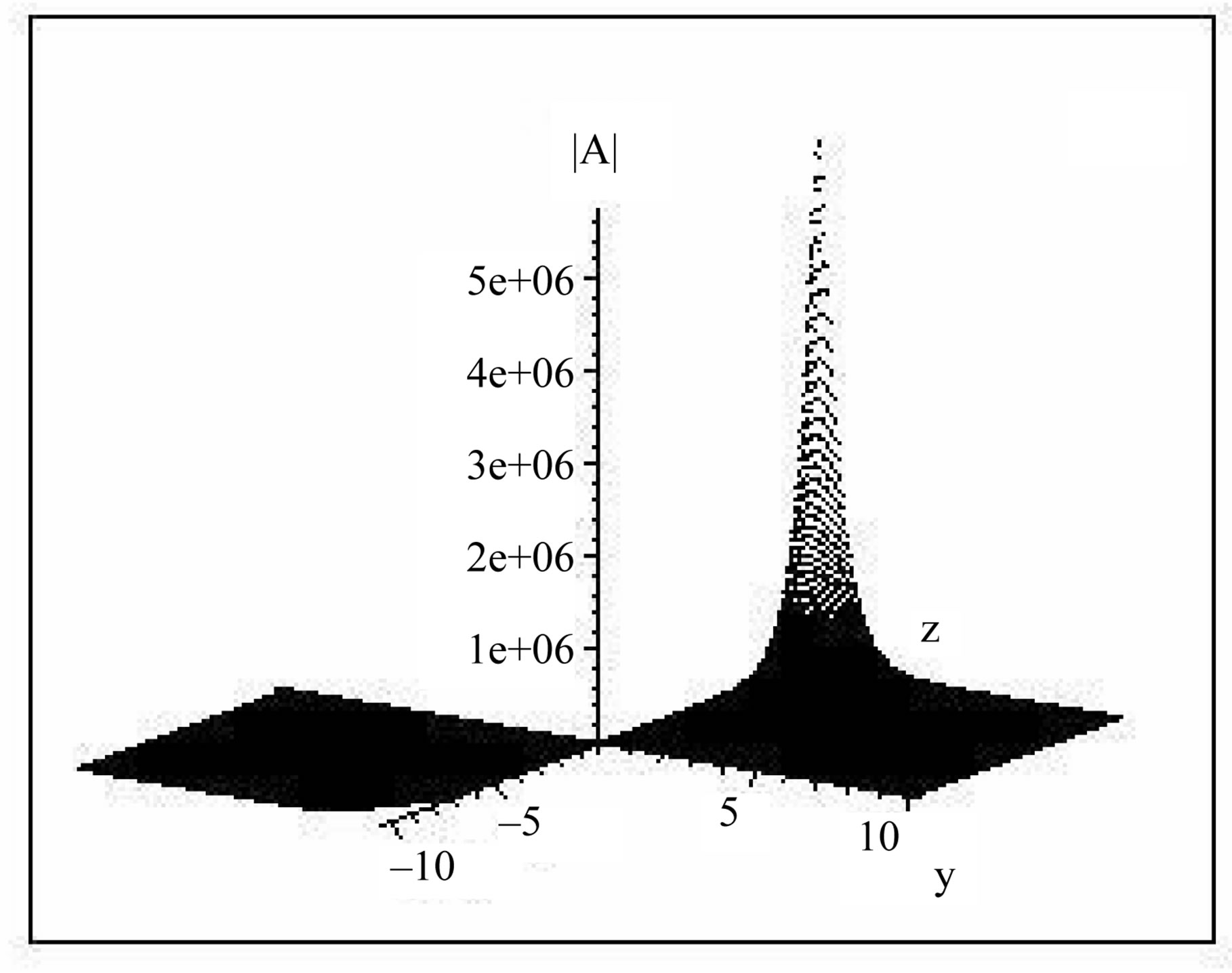 (c)
(c)
Figure 2. The field distribution of the nonlinear surface waves A(y, z) for (a) ω/2π = 4.3 GHz, growth rate d = 0.626; (b) (ω/2π) = 5.6 GHz, d = 1.337*I & (c) ω/2π = 5.9 GHz, d = 1.347*I for μp = 0.3, ωp/2π = 10 GHz, ω0/2π = 4 GHz, ε3 = 2.25 & propagation distance x = 3.
rate of perturbation 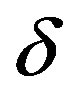 is real (
is real ( = 0.626). The decay constant of NSW in nonlinear medium
= 0.626). The decay constant of NSW in nonlinear medium  = 3.708 and the decay constant of NSW in linear medium
= 3.708 and the decay constant of NSW in linear medium  = 1.39, t = 0.3755 as computed from Equations (4b), (6b) & (12b), respectively. For increasing values of (
= 1.39, t = 0.3755 as computed from Equations (4b), (6b) & (12b), respectively. For increasing values of (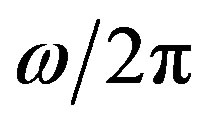 ) to (5.6GHz and 5.9 GHz) the
) to (5.6GHz and 5.9 GHz) the  changes to the values (–2.19, –1.875) while
changes to the values (–2.19, –1.875) while  changes to the values (–0.144, –0.037), the
changes to the values (–0.144, –0.037), the  is increased to (3.96, 3.99) and
is increased to (3.96, 3.99) and 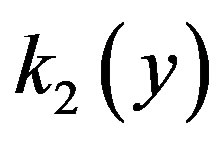 is constant because
is constant because  is constant, t is increased to (1.0679, 1.076) so, the growth rate
is constant, t is increased to (1.0679, 1.076) so, the growth rate  becomes imaginary of values (1.337*I, 1.347*I) respectively. The field distribution is sharpened where the wave’s turns from unstable to stable waves and concentrated in the non linear medium. This means that the stability of the waves is affected with the wave frequency.
becomes imaginary of values (1.337*I, 1.347*I) respectively. The field distribution is sharpened where the wave’s turns from unstable to stable waves and concentrated in the non linear medium. This means that the stability of the waves is affected with the wave frequency.
Figures 3(a)-(c) display the spatial evolution of steady state field amplitude ,
,  as a function of the refractive index
as a function of the refractive index . I found that at wave frequency (
. I found that at wave frequency ( ),
),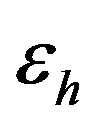 is of value (–3.169) &
is of value (–3.169) &  is of value (–0.682). At
is of value (–0.682). At 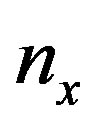 = 3, the perturbed waves are stable where the growth rate of perturbation
= 3, the perturbed waves are stable where the growth rate of perturbation  is imaginary (
is imaginary ( = 0.8266*I). The decay constant of NSW in nonlinear medium
= 0.8266*I). The decay constant of NSW in nonlinear medium  = 2.598 and the decay constant of NSW in linear medium
= 2.598 and the decay constant of NSW in linear medium  = 2.615, t = 1.006. For increasing value of
= 2.615, t = 1.006. For increasing value of  to (4.5) the
to (4.5) the  is increased to (4.253) &
is increased to (4.253) & 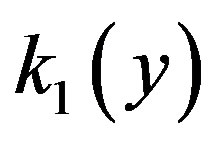 is increased to (4.242) and t is decreased to (1.002) so, the growth rate
is increased to (4.242) and t is decreased to (1.002) so, the growth rate  still imaginary of value (1.463*I) respectively where the waves shifted to the nonlinear medium, with the subsequent excitation of the nonlinear stable surface waves of high energy (soliton). At
still imaginary of value (1.463*I) respectively where the waves shifted to the nonlinear medium, with the subsequent excitation of the nonlinear stable surface waves of high energy (soliton). At  = 5, the perturbed waves still stable of decreasing energy, the growth rate of perturbation (
= 5, the perturbed waves still stable of decreasing energy, the growth rate of perturbation ( = 1.664*I). The decay constant of NSW in nonlinear medium
= 1.664*I). The decay constant of NSW in nonlinear medium  = 4.778 and the decay constant of NSW in linear medium
= 4.778 and the decay constant of NSW in linear medium 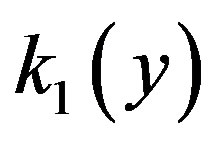 = 4.769, t = 1.0019. Figure 4, illustrates the energy flow
= 4.769, t = 1.0019. Figure 4, illustrates the energy flow 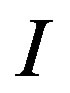 of the nonlinear surface waves as a function of
of the nonlinear surface waves as a function of  for various values of
for various values of . For
. For  = 0.1, the wave’s energy is increased by increasing
= 0.1, the wave’s energy is increased by increasing  where the waves are forward traveling. For increasing value of
where the waves are forward traveling. For increasing value of 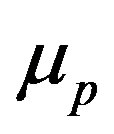 to (0.3), the high wave energy is concentrated at
to (0.3), the high wave energy is concentrated at 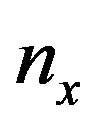 = 4.5 of forward traveling & then decreases by increasing
= 4.5 of forward traveling & then decreases by increasing . It shows that at values of
. It shows that at values of , the energy becomes negative, where the waves can be switched to the backward propagation as an effect of the LHM.
, the energy becomes negative, where the waves can be switched to the backward propagation as an effect of the LHM.
These results are different from that obtained for the magnetic medium such as lateral antiferromagnetic/nonmagnetic superlattice (LANS) [14] and gyrodielectric medium as a semiconductor [13]. The existence of the magnetic matter causes the growth rate to be always real and the waves are always unstable. For a semiconductor substrate, the waves are stable of forward traveling.
4. Conclusions
The stability characteristics of nonlinear surface waves
 (a)
(a) (b)
(b) (c)
(c)
Figure 3. The field distribution of the nonlinear surface waves A(y, z) for (a) nx = 3, growth rate d = 0.8266; (b) nx = 4.5, d = 1.463*I and (c) nx = 5, d = 1.664*I for μp = 0.3, ωp/2π = 10 GHz, ω/2π = 4.9 GHz, ω0/2π = 4 GHz, ε3 = 2.25 and propagation distance x = 3.
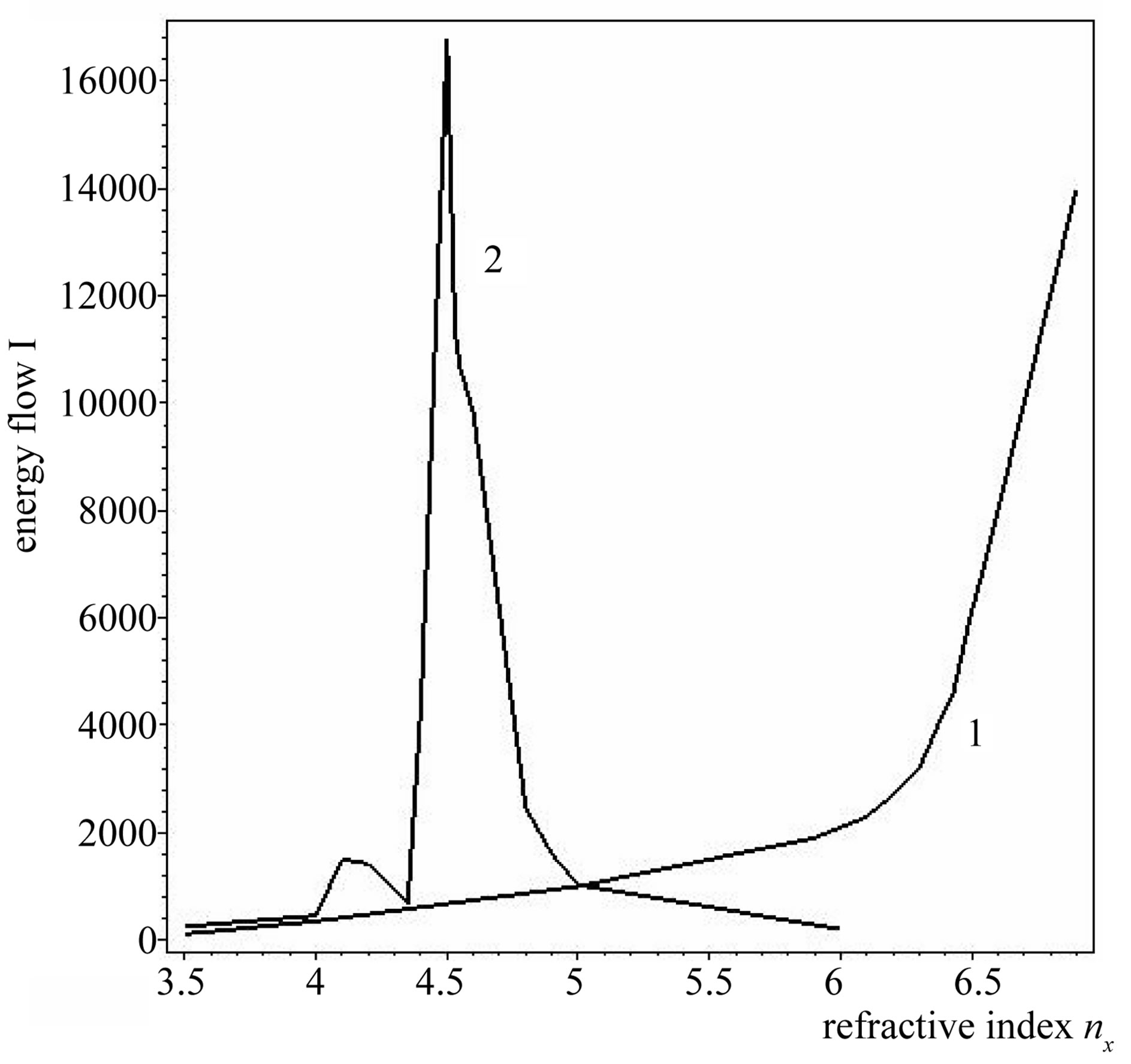
Figure 4. The energy flow I of the nonlinear surface waves as a function of nx for (1) μp = 0.1 and (2) μp = 0.3, ωp/2π = 10 GHz, ω/2π = 4.9 GHz, ω0/2π = 4 GHz, ε3 = 2.25 and propagation distance x = 3.
propagating along a left-handed substrate(LHM) and a non-linear dielectric cover are investigated. I found that, the stability of the waves in LHM can be controlled by the frequency dependence of the electric permittivity and magnetic permeability of the LHM. By increasing the effective refractive index at fixed saturation parameter, the field distribution is sharpened which is implying the possibility of optical switching and the field concentrated in the nonlinear medium (optical soliton) which is useful for practical ultrahigh-speed communications. At higher values of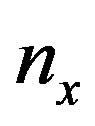 , attenuated backward waves are observed. I believe that the stability which has been investigated and reported here may provide new opportunities for the design of future microwave-photonic devices.
, attenuated backward waves are observed. I believe that the stability which has been investigated and reported here may provide new opportunities for the design of future microwave-photonic devices.
REFERENCES
- L. Hu and S. T. Chui, “Characteristics of Electromagnetic Wave Propagation in Uniaxially Anisotropic Left-Handed Materials,” Physical Review: B, Vol. 66, No. 8, 2002, pp. 085108-085115. doi:10.1103/PhysRevB.66.085108
- V. G. Veselago, “The Electrodynamics of Substances with Simultaneously Negative Values of Permittivity and Permeability,” Soviet Physics Uspekhi, Vol. 10, No. 4, 1967, p. 509. doi:10.1070/PU1968v010n04ABEH003699
- I. V. Shadrivov, A. A. Sukhorakov and Y. S. Kivshar, “Nonlinear Surface Waves in Left-Handed Material,” Physical Review: E, Vol. 69, No. 1, 2004, p. 016617. doi:10.1103/PhysRevE.69.016617
- D. R. Smith, W. J. Padilla, D. C. Vier, S. C. Nemat-Nasser and S. Schultz, “Composite Medium with Simultaneously Negative permeability and Permittivity,” Physical Review Letters, Vol. 84, No. 18, 2000, p. 4184. doi:10.1103/PhysRevLett.84.4184
- J. V. Moloney, J. Ariyasu and G. I. Stegeman, “Stability of Nonlinear Stationary Waves Guided by a Thin Film Bounded by Nonlinear Media,” Applied Physics Letter, Vol. 48, No. 13, 1986, p. 826. doi:10.1063/1.96680
- H. T. Tran, “Stability of Stationary Dark Waves Guided by Nonlinear Surfaces and Waveguides,” Journal of the Optical Society of America B, Vol. 11, No. 5, 1994, pp. 789-797. doi:10.1364/JOSAB.11.000789
- N. Akhmediev, A. Ankiewicz and H.-T. Tan, “Stability Analysis of Even and Odd Waves of Symmetric Nonlinear Planar Optical Waveguides,” Journal of the Optical Society of America B, Vol. 10, No. 1, 1993, pp. 230-236. doi:10.1364/JOSAB.10.000230
- N. N. Akhmediev, “Nonlinear Surface Electromagnetic Phenomena,” In: H. E. Ponath and G. I. Stegeman, Eds., The Problem of Stability and Excitation of Nonlinear Surface Waves, Elsevier, Horth Holland, 1991, p. 289.
- A. Hasegawa, “Soliton Effects in Optical Waveguides,” Reports on Progress in Physics, Vol. 65, No. 6, 2002, pp. 999-1024. doi:10.1088/0034-4885/65/6/203
- A. A. Sukhorukov, Y. S. Kivshar, H. S. Eisenberg and Y. Silberberg, “Spatial Optical Solitons in Waveguide Arrays,” IEEE Journal of Quantum Electron, Vol. 39, No. 1, 2003, pp. 31-50. doi:10.1109/JQE.2002.806184
- M. Johansson, A. A. Sukhorukov and Y. S. Kivshar, “Discrete Reduced-Symmetry Solitons and Second Band Vortices in Two Dimensional Nonlinear Waveguide Arrays,” Physical Review: E, Vol. 80, No. 4, 2009, pp. 046604- 046619. doi:10.1103/PhysRevE.80.046604
- F. Setzpfandt, A. A. Sukhorukov and T. Pertsch, “Discrete Quadratic Solitons with Competing Second-Harmonic Components,” Physical Review A, Vol. 84, No. 5, 2011, pp. 053843-053851. doi:10.1103/PhysRevA.84.053843
- H. M. Mousa and M. M. Shabat, “Stability of Nonlinear Te Surface Waves along the Boundary of Linear Gyrodielectric Media,” International Journal of Modern Physics B, Vol. 21, No. 26, 2007, pp. 4487-4493. doi:10.1142/S0217979207038009
- M. M. Shabat and H. M. Mousa, “Stability of Nonlinear Te Surface Waves along the Interface of Nonlinear Dielectric and Superlattices Media,” The Islamic University Journal, Vol. 14, No. 1, 2006, pp. 135-145.
- “Maple Software,” Version 9, 615 Kumpf Drive, Waterloo, 2004.

