Int'l J. of Communications, Network and System Sciences
Vol.7 No.1(2014), Article ID:42450,10 pages DOI:10.4236/ijcns.2014.71006
Image Encryption Scheme Based on Filter Bank and Lifting
1Department of Communications and Electronic Engineering, Philadelphia University, Amman, Jordan
2Department of Computer Engineering, Mu’tah University, Karak, Jordan
3Department of Computer Science, Applied Science University, Amman, Jordan
4Department of Electrical Engineering, The University of Jordan, Amman, Jordan
Email: Saleh_53@yahoo.com
Copyright © 2014 Saleh Saraireh et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Saleh Saraireh et al. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
Received November 27, 2013; revised December 27, 2013; accepted January 4, 2014
KEYWORDS
Randomness Test; Image Encryption; Encryption Quality; Filter Bank; Entropy
ABSTRACT
In this paper, the quality of image encryption using filter bank with lifting scheme has been studied and evaluated. Many extensive techniques have been applied to examine the security of the image encryption using the filter bank cipher with one or two rounds. To analyze and evaluate the proposed scheme, many parameters have been employed, such as, histogram analysis, correlation coefficient, global entropy, block entropy, avalanche effect, number of pixel change rate (NPCR), unified average change intensity (UACI), compression friendliness, exhaustive key analysis, and key sensitivity test. The simulation results showed that, the quality of the image encryption passes all these tests. Moreover, it reaches or excels the current state-of-the-arts. So that, the proposed image encryption process produces random-like output from the statistical point of views.
1. Introduction
Due to the rapid advances in computer and communication networks and the recent progress in multimedia technologies (i.e. audio, video, image, etc.), multimedia information can easily be exchanged over different types of networks like the Internet. Usually, these networks are not secure. Therefore, users must pay more attention to the security of their networks and information transmission against unauthorized users. Due to this, the multimedia information security has become a vital concern in military applications, audio and videoconferencing, imaging, E-Commerce, and mobile phone applications [1,2]. Moreover, over these networks, people may be required to send personal and sensitive information or exchange important documents. In such situations; security, integrity, authenticity and confidentiality of digital data should be provided. Therefore, these applications must be secured from various kinds of attacks like interruption, interception, modification and fabrication [3,4]. As a result, it is essential to protect this information using some encryption and cryptography algorithms.
Encryption (enciphering) is a procedure utilized for converting and scrambling of data to insure its security. Consequently, several security approaches have been proposed to insure the required protection [2]. The use of these security techniques allows the information transmission across insecure networks to prevent any danger of attack. Cryptology and cryptanalysis are two major kinds of cryptography, where the cryptology is to keep plaintext secret from eavesdropper while cryptanalysis is to conquer such techniques to reconstruct this information [3].
The process of encryption includes that the multimedia data is protected and a key is provide for decryption process (deciphering). The encrypted data are usually called the ciphertext and unencrypted data are called the plain-text. To decide whether one is allowed to view the encrypted data or not, a key is used. Based on this point, there are two main types of algorithms used for data encryption; symmetric-key algorithms and public key algorithms. In the symmetric algorithms, the encryption and decryption keys are similar while in public key algorithms, the keys are different. Nowadays, the key is the core of most encryption algorithms [5].
A further classification of an encryption algorithm can be block cipher and stream cipher [6]. A block cipher is a symmetric key cipher which takes a block of plaintext as an input and the output is another ciphertext block of the same length. Whereas, a stream cipher takes the data one bit or one byte at a time. Due to this, the stream cipher is much faster than the block cipher and with less hardware complexity [6]. While, block cipher is better than the stream ciphers in that the data block can be serially encrypted by decimating large blocks into several smaller blocks [6]. In [6], filter bank systems were employed as a cryptosystem, where the analysis filter banks were used to make the encryption process, while the synthesis filter banks were used to make the decryption process.
Digital image is one of the most important fields of multimedia applications. Additionally, because of the growing demand in using images in industrial, business, medical imaging, and military aspects, it is critical to guard and protect the confidential image information. An image is a two-dimensional array which can be converted into a one dimensional bit stream which is usually considered as text. By this any traditional cryptographic scheme may be utilized. However, images are not like text due to large data size, higher degrees of redundancy, and strong correlation among pixels which will require high computational and processing times and which not suitable for real-time communications [2]. Moreover, text conventional cryptography systems are built in a way that the text is required to be recovered exactly which is not the case for image where the content of the image is the required not the exact pixels values. Therefore, an approximation of the transmitted image is adequate and small amount deformation and noise is satisfactory due to human visual perception [7]. Therefore, new efficient image encryption algorithms are required urgently. Image encryption techniques are basically classified into three categories [8]
1) Position permutation: in this method the order of the pixels, bits or blocks of an image is changed randomly so that the image will be not visible and usually have low security.
2) Value transformation: this approach is based on a binary sequence (i.e., a key) generation from a chaotic system. This key is used for encryption and decryption of every image pixel and has low computational complexity and low hardware cost.
3) Combination of 1 and 2 above: This is a combination of both position permutation and value transformation approaches where pixels, bits or blocks are firstly reordered and then a key is used to change the values. This usually has the potential of high security.
Recently, variety of different image encryption techniques have been proposed but no significant algorithm suit all different image types and applications [9]. Following, a brief discussion of recent image encryption schemes is provided.
In [10], authors analyzed and modified the Advanced Encryption Standard (AES). The modification included an addition of a new key stream generator (A5/1, W7) to the ordinary AES which resulted in improving the encryption algorithm performance. Similarly, a detailed and modified approach of the AES algorithm was provided in [11] to produce a high level security and better image encryption than the ordinary AES.
A block-based transformation algorithm by combining of image transformation and Blowfish algorithm was devised based on dividing the original image into blocks [12]. These blocks were then rearranged and transformed via a transformation algorithm and encrypted using the Blowfish algorithm. The results illustrated that the correlation between image elements was significantly decreased and using smaller block sizes resulted in an even lower correlation and higher entropy.
A combination of an image permutation and an encryption algorithm called RijnDael, based on dividing the image into blocks of 4 × 4 pixels sizes, was presented in [13]. Then these were rearranged to form a permuted image by permutation process. The permuted image was encrypted by RijnDael algorithm. This produced a considerable decrease in correlation among image elements and higher entropy. Another study offered an image encryption algorithm using random pixel permutation [14]. The algorithm included: image encryption, key generation phase, and identification process. This presented security to colored image with less computations and more effectiveness.
An advanced Hill (AdvHill) cipher algorithm utilizing an involutory key matrix for encryption was in proposed [15]. Using this algorithm, unlike the ordinary Hill ciphering algorithm, it was possible to cipher any image with different gray scales in addition to the colored images.
A novel algorithm for image ciphering based on SHA- 512 hash function was devised in [16]. The algorithm was composed of two parts: firstly, preprocessing operation to shuffle one half of image. Secondly, hash function was used to generate a random number mask. This mask was XORed with the other part of the image which is going to be encrypted. Another scheme which utilized the XOR function was introduced in [17]. The proposed algorithm employed the affine transform to shuffle the original image pixels. The shuffled image was encrypted using XOR operation. Then using four 8-bit keys, the pixel values were distributed to different location using affine transform. In addition, an algorithm which provided a simple encryption technique based on using two simple Boolean operations: XOR and Rotation [9]. It included several times of a sequential XORing on all pixels bits and a circular rotating right of these bits were performed. The results showed that the method results a high secure image.
In [18], a chaos-based stream cipher algorithm was devised. It consisted of two chaotic logistic maps and a large enough external secret key. A secret key of 104 bit and two chaotic logistic maps were used to puzzle the relationship between the cipher image and the plain image. In addition, to increase the robustness of the algorithm, the key is changed after each pixel encrypting. It was proved that the correlation among pixel values was significantly decreased. Moreover, Chaotic Map with Block Chaining (CMBC) image encryption using logistic chaotic maps and cipher block chaining (CBC) was introduced [19]. This approach showed that the algorithm is unbreakable for most of the well-known attacks. In addition, CMBC security system was superior to other systems but with slight increase in encryption time. Another new non-chaotic image encryption approach based on a secret key of 144-bits was developed in [20]. It employed both pixel substitution and permutation processes. Moreover, feedback mechanism was used to increase the algorithm robustness and avoids differential attack. It showed that the devised scheme possessed a high encryption rate, required less computation and sensitive to secret keys. Genetic algorithms were also used in image encryption. In [21], a hybrid model of a genetic algorithm and a chaotic function was devised. This technique, first encrypt a number of images using a chaotic function. Then, these images were used as the initial population of the genetic algorithm. The genetic algorithm is used to optimize the encrypted images as much as possible. The best cipher-image is selected as the optimum (best) encryption image.
In [22], an algorithm based on using the idea DNA subsequence operations combined with the logistic chaotic map to distribute pixels values and location of an image to be encrypted was introduced. The results proved that the proposed algorithm had good encryption efficiency with limited abilities in attack resistivity.
In this paper, a filter bank cipher is used as an image ciphering scheme in order to enhance the security level of the encrypted images. The remainder of this paper is organized as follows. In Section 2, a background of the main parameters that are usually used to evaluate and analyze image encryption schemes is provided. Section 3 describes the proposed image encryption scheme. Section 4 presents the experimental results and discussion. Finally, Section 5 concludes the paper.
2. Background
2.1. Parameters for Analysis and Assessment of an Image Encryption Algorithm
There are some specific parameters that can be used to evaluate the effectiveness and robustness of any proposed image encryption technique. These parameters include:
2.1.1. Histogram Analysis
One of the main characteristics of any image encryption scheme is to produce a random-like plaintext image [4]. This can be checked by histogram analysis which displays how image pixels are distributed with respect to the color or gray scale intensity level. The histogram of the cipher image must be uniformly distributed in order not to provide any sign for possible statistical attack. Histogram of the encrypted image is very different from that the original image. Usually, the original image histograms contain large spikes due to pixels gray scale values [2].
2.1.2. Correlation Coefficient Analysis
Correlation is a factor that determines how much two variables are similar to each other. This is commonly used to measure the encryption quality of any cryptography scheme [2]. The strength and usefulness of any encryption technique is measured by its ability to conceal all attributes of the original data and to produce an encrypted data which is totally random and uncorrelated with the original one [11]. In image processing, usually, the correlation among adjacent pixels of original image is very high (i.e., equal to 1). On other hand, for image encryption, the correlation between the encrypted and original image pixels should be very low with values approaching to zero. Therefore, an efficient image encryption algorithm should reduce this coefficient as much as possible to be near zero. Assume x and y are values of two pixels in the original and the cipher image and both are in same location. The correlation coefficient  is computed as follows [11]:
is computed as follows [11]:
 (1)
(1)
 (2)
(2)
 (3)
(3)
 (4)
(4)
 (5)
(5)
 (6)
(6)
Where x and y are the values of two pixels in the same location in the original and ciphered images, respectively.  is covariance at these pixels.
is covariance at these pixels.  and
and  are variance values at pixel values x and y in both the original and the cipher images respectively.
are variance values at pixel values x and y in both the original and the cipher images respectively.  and
and  are standard deviations of both x and y pixel values,
are standard deviations of both x and y pixel values,  is the expectation operator and N × N is the image dimension.
is the expectation operator and N × N is the image dimension.
2.1.3. Entropy Analysis
Entropy is one of the significant measures for evaluating any encryption system. Information entropy shows the degree of uncertainties and randomness in systems like cryptography, network security, and data compression [2]. The entropy,  of any data is defined as [2]:
of any data is defined as [2]:
 (7)
(7)
where  is the probability of occurrence of the symbol mi.
is the probability of occurrence of the symbol mi.
Using the above equation, if each symbol has equal probability and every symbol is represented by 8 bits, then  which is the ideal situation. For image encryption, the value of
which is the ideal situation. For image encryption, the value of  is usually less than the ideal value, which means an efficient encryption algorithm should provide entropy values very near to the ideal case in order to be able to resist any entropy attack [2].
is usually less than the ideal value, which means an efficient encryption algorithm should provide entropy values very near to the ideal case in order to be able to resist any entropy attack [2].
Sometimes, high entropy values are not adequate to ensure that the encrypted image is totally random-like. Therefore, another randomness and uncertainty measure that can be employed for further image ciphering analysis is called the block entropy test [11]. This test provides both qualitative and quantitative results [11]. Block entropy test divides image into K blocks and calculates entropy for every block  using Equation (7) rather than the whole image entropy
using Equation (7) rather than the whole image entropy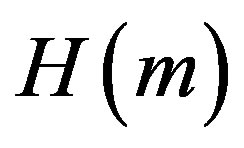 . Then calculates the mean entropy of the K block entropies as follows [2]:
. Then calculates the mean entropy of the K block entropies as follows [2]:
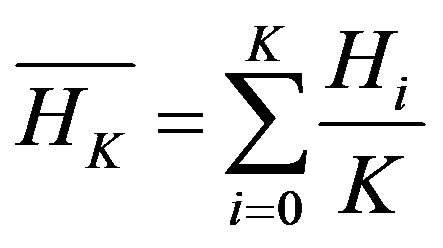 (8)
(8)
2.1.4. Diffusion Characteristics
Diffusion is one of the most important characteristics of any cryptosystem. This concept was firstly brought by C. E. Shannon in 1949 [23]. Diffusion implies that if any bit (even single bit) of the plaintext or the key has been changed, then ciphertext will be changed directly. This also applies for the image encryption, where any bit change in the key will result in a vital change in the encrypted image. This is also known as the Avalanche Effect. Using stringent avalanche effect will cause a change of at least 50% in the ciphertext image due to a one bit change in the plaintext image. Mean Square Error (MSE) is one of the most commonly used measures of the avalanche effect. MSE is the average squared difference between two images. It is computed pixel-by-pixel as follows [2]:
 (9)
(9)
where I and K are two ciphertext images with keys differ by one bit. M and N are the dimensions of the images. i and j are pixel positions within the images.
Other measures of the diffusion are the Number of Pixel Change Rate (NPCR) and Unified Average Change Intensity (UACI) [12,20]. NPCR and UACI were firstly shown in 2004 [24]. Since that both NPCR and UACI have been commonly used in analyses of the image encryption schemes. The NCPR computes the ratio of different pixels between the plaintext and the ciphertext images as follows [12].
 (10)
(10)
where

I, K, M, N, I, and j are as defined in Equation (9).
UACI computes the number of averaged changed intensity between ciphertext images [2]. UACI can be calculated as [2]:
 (11)
(11)
The higher the value of NPCR and UACI, the better the designed algorithm is.
2.1.5. Key Space Analysis
An effective image encryption technique must be sensitive to encrypting keys [1]. There two ways to test the keys used in encryption process: Exhaustive Key Search and Key Sensitivity Test:
1) Exhaustive Key Search: A secure encryption algorithm should have a large key space. The larger the key space, the less the attacks on encryption design are [6]. If an algorithm has k-bit key, then the exhaustive key search needs 2k trials to break the key. If k is 128 bit, then 2128 operations are required to discover the correct key.
2) Key Sensitivity Test: Key sensitivity test determines if a ciphered image is sensitive with respect to changes in the key. In a good cryptosystem, a decryption mechanism must not decrypt ciphertext image appropriately, even if a single bit is changed in the key [25]. This means that even large keys are employed; key sensitivity is necessary for cryptosystems.
3. Filter Bank as an Image Encryption System: Approach
In this paper, a filter bank cipher is employed as a scheme for image encryption. In this system, the encryption process is carried out using the analysis filter bank while the decryption process is achieved using the synthesis filter bank. This means that the encryption and the decryption processes are based on a “linear” circular convolution process, which is well-known to provide an excellent diffusion. To add the necessary nonlinearity (confusion) to the cipher, a lifting scheme is used with a nonlinear function over GF(28) [6]. The encryption and decryption process are shown in Figures 1 and 2 for one round cipher, respectively [6]. The image encryption analysis is performed using one and two rounds of the cipher to examine the security of the image at each stage.
Filter bank cipher has many advantages [6]. Its implementation is simple, since it is based on digital filter design, which offers a high speed implementation in software and hardware. Also, it offers a high security level using small number of rounds. In addition, the most important is the scalability of this cipher, as it can deal with different length of key or plaintext which can be adjusted according to a particular encryption application.
4. Experimental Results and Discussion
4.1. Histogram Analysis
The histogram can be employed to illustrate the quality of image encryption. A secure image encryption system should produce a uniformly distributed histogram of the encrypted image. Figures 3 and 4 present the histograms representation of the original and the encrypted image using different number of rounds. Note that, the histograms of the images after the encryption process have a uniform distribution. As a result, the encrypted images are random-like.
4.2. Correlation Coefficients Analysis
Correlation coefficient is usually employed to measure the relationship between the original image and the encrypted image to determine the encryption quality. If the correlation coefficient is very close to zero, it means that, the relationship between the two images is very weak. The correlation coefficients have been calculated between two horizontally adjacent pixels, two vertically adjacent pixels and two diagonally adjacent pixels of the original and encrypted images using 1000 randomly selected pairs of two adjacent pixels using Equation (1). The tests have been applied into Lenna and House images, where the size of the images is 256 × 256 pixels. Tables 1 and 2 illustrate the results for Lenna and House

Table 1. Correlation coefficient of two adjacent pixels for Lenna image.

Table 2. Correlation coefficient of two adjacent pixels for House image.

Figure 1. One round for filter bank encryption system.

Figure 2. One round for filter bank decryption system.
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 3. (a) Original House image; (b) Encrypted image using one round; (c) Encrypted image using two rounds; (d) Histogram of the original image; (e) Histogram of encrypted image using one round; (f) Histogram of encrypted image using two rounds.
 (a)
(a) (b)
(b) (c)
(c) (d)
(d)
Figure 4. (a) Original Lenna image; (b) Encrypted image using one round; (c) Encrypted image using two rounds; (d) Histogram of the original image; (e) Histogram of encrypted image using one round; (f) Histogram of encrypted image using two rounds.
images, respectively.
It can be noticed that, the horizontal, vertical and diagonal correlation coefficients for the original images are close to 1 (maximum correlation coefficient), while the correlation coefficients values for the encrypted images are very closed to zero. This means that, after the encryption process, the highly correlated adjacent pixels of the original images have been completely broken in all directions. It is clear that, for horizontally adjacent pixel of Lenna image, the horizontal correlation coefficient is 0.9267 while it is −0.0081 for the encrypted image. Consequently, the horizontally adjacent pixels after the encryption process are uncorrelated. The same results have been obtained for vertical and diagonal directions as summarized in Table 1 for Lenna image and Table 2 for House image.
4.3. Information Entropy Analysis
Entropy is a quantitative measure of signal randomness. Basically, the global information entropy for gray scale should be 8 bits. So, the global entropy at output of the encryption scheme should be very close to 8 bits, otherwise, the security of the encryption scheme is threaten. The simulation results based on Equation (7) for global information entropy test are summarized in Tables 3 and 4 using different number of rounds, different images and different keys. The results indicate that, the global entropy is very close to the theoretical values (8 bits).
Block entropy rather than global entropy is used to measure the local entropy over images blocks. To measure the block entropy, a randomly 100 non-overlapping blocks have been selected from the encrypted images. Then, the entropy for each block is calculated and recorded and the average is taken to find the block entropy using Equation (8). The results of block entropy are shown in Tables 5 and 6. The results indicate that, the encrypted images become random-like after encryption, since they have higher block entropy when compared with the minimum theoretical critical block entropy.

Table 3. Global entropy for the House image.

Table 4. Global entropy for the Lenna.
4.4. Diffusion Characteristics
4.4.1. Avalanche Effect
The avalanche effect means that any small change in the key or the plaintext should give a huge and significant change to the corresponding ciphertext. To examine the diffusion characteristics, two images have been encrypted using the same key. Then, the same key with a slight change (one bit differ) in the original image and encrypt them. Using Equation (9), the MSE is calculated to check the influence of the one bit change in the original image. The simulation results in Table 7 proved that, the MSE > 30 dB [26] which means, a slight difference in the original images yields a significant change to the ciphertext which satisfies the diffusion principle.
4.4.2. NPCR and UACI
NPCR and UACI are qualitative randomness tests, and both can be used to evaluate the resistance of the encrypted image against the differential attack. NPCR is used to compute the number of different pixel to the total number of pixels. UACI measure the average intensity of the differences between the images. The result for NPCR and UACI are computed using Equations (10) and (11), respectively. These results are summarized in Table 8, which demonstrate that, a good diffusion characteristics have been obtained after a small change in the images.

Table 5. Block entropy for the encrypted House image.

Table 6. Block entropy for the encrypted Lenna image.

Table 7. MSE results.

Table 8. NPCR and UACI results.
So, the encrypted image is very sensitive to any change in the original image, as a result a strong diffusion has been done, and the encrypted images are very like-random.
4.5. Key Space Analysis
A strong image encryption scheme must be very sensitive to the key. Two methods are used to evaluate the key space analysis.
4.5.1. Exhaustive Key Analysis
The minimum key length that has been used to encrypt the images is 128. If an attacker uses 1000 MIPS computer to break the key using the brute force attack, the attacker needs
 Years This is very long time period which is infeasible [2].
Years This is very long time period which is infeasible [2].
4.5.2. Key Sensitivity Test
This test measures the sensitivity of the encrypted image due to a minor change of the key. Suppose that, there are two keys which differ only in one bit. Then, the encryption process has been performed for the images (Lenna and House). Figures 5 and 6 show the sensitivity of the encrypted images to the small change of the key (key 1 and key 2 with one bit differs). As a result, the confusion property is satisfied over the encrypted images using both one and two rounds. The corresponding percentage differences between two encrypted images with one bit differ in the key for Lenna and House images are calculated as depicted in Table 9.
4.6. Statistical Comparison Results
The simulation results for two rounds filter bank cipher are compared with two image encryption ciphers; namely, advanced encryption standard (AES) and Compression Friendly Encryption Scheme (CFES). The values in Table 10 demonstrate that, the filter bank cipher is stronger than CFES; in addition it has the same results as AES and some results better than the AES results. Moreover, the filter bank cipher supports simpler implementation and scalability.
5. Conclusion
In this paper, many evaluation parameters were used to analyze the image encryption quality using filter bank cipher with one and two rounds. The evaluation parameters are histogram analysis, correlation coefficient, global entropy, block entropy, avalanche effect, NPCR, UACI, compression friendliness, exhaustive key analysis, and key sensitivity test. The simulation results for histogram

Table 9. Difference of two ciphers when keys differ by one bit results.
 (a)
(a) (b)
(b)
Figure 5. (a) Original House image; (b) Encrypted image using key 1 using one round (C1); (c) Encrypted image using key 2 using one round (C2); (d) Cipher image difference |C1 – C2|; (e) Encrypted image using key 1 using two rounds (C3); (f) Encrypted image using key 2 using two rounds (C4); (g) Cipher image difference |C3 – C4|.
 (a)
(a) (b)
(b)
Figure 6. (a) Original Lenna image; (b) Encrypted image using key 1 using one round (C1); (c) Encrypted image using key 2 using one round (C2); (d) Cipher image difference |C1 – C2|; (e) Encrypted image using key 1 using two rounds (C3); (f) Encrypted image using key 2 using two rounds (C4); (g) Cipher image difference |C3 – C4|.

Table 10. Parameters evaluation comparison with AES and CFES.
showed that the distribution of the encrypted image is uniform. In correlation coefficient analysis, the correlated adjacent pixels of the original images are completely distributed in the encrypted image with very small correlation coefficient in all directions (horizontal, vertical and diagonal). The global and block entropy are very close to ideal, so the encrypted image represent random—like image. Also, the diffusion characteristics were proved through avalanche test, NPCR and UACI. The key sensitivity results showed that image encryption scheme is very sensitive to the key change. Accordingly, the image encryption process is able to pass all these tests; as a result, the encryption process is considered as a strong and robust process to resist many existing cryptography attacks and cryptanalysis technique. Also, the results are compared with other image cipher schemes and the filter bank cipher shows that it’s dominant. To ensure the image encryption security and immunity against cryptanalysis technique, it is better to use two rounds filter bank cipher even the result for one round shows good security.
REFERENCES
- S. Saraireh, “A Secure Data Communication System Using Cryptography and Steganography,” International Journal of Computer Networks & Communications (IJCNC) Vol. 5, No. 3, 2013, pp. 125-137.
- S. Saraireh, M. Saraireh and Y. Al-Sbou, “Secure Image Encryption Using Filter Bnak and Addition Modulo 28 with Exclusive OR Combination,” International Journal of Computer Science and Security (IJCSS), Vol. 7, No. 2, 2013, pp. 66-80.
- W. Stallings, “Cryptography and Network Security: Principles and Practice,” Prentice Hall, Upper Saddle River, 2010.
- J. Ahmad and F. Ahmed, “Efficiency Analysis and Security Evaluation of Image Encryption Schemes,” International Journal of Video & Image Processing and Network Security, Vol. 12, No. 4. 2012, pp. 18-31.
- A. Kahate, “Cryptography and Network Security,” 2nd Edition, Tata-McGraw-Hill, Noida, 2008.
- S. Saraireh and M. Benaissa, “A Scalable Block Cipher Design Using Filter Banks and Lifting over Finite Fields,” IEEE International Conference on Communications (ICC), Dresden, 14-18 June 2009, pp. 1-5.
- F. Ahmed, M. Siyal and V. Abbas, “A Perceptually Scalable and JPEG Compression Tolerant Image Encryption Scheme,” IEEE Symposium in Image and Video Technology (PSIVT), Singapore City, 14-17 November 2010, pp. 232-238.
- P. Sharma, M. Godara and R. Singh, “Digital Image Encryption Techniques: A Review,” International Journal of Computing & Business Research, GKU/ISociety12/046, 2012, pp. 2229-6166.
- M. Abbas and F. Al-Husainy, “A Novel Encryption Method for Image Security,” International Journal of Security and Its Applications, Vol. 6, No. 1, 2012, pp. 1-9.
- M. Zeghid, M. Machhout, L. Khriji, A. Baganne and R. Tourki, “A Modified AES Based Algorithm for Image Encryption,” World Academy of Science, Engineering and Technology, Vol. 3, 2007, pp. 526-536.
- K. Seyed, H. Shakerian, R. Hedayati and M. R. Mohsen, “New Modified Version of Advance Encryption Standard Based Algorithm for Image Encryption,” International Conference on Electronics and Information Engineering, Kyoto, 1-3 August 2010.
- M. A. Bani Younes and A. Jantan, “Image Encryption Using Block-Based Transformation Algorithm,” IAENG International Journal of Computer Science, Vol. 35, No. 1, 2008.
- M. Younes and A. Jantan, “An Image Encryption Approach Using a Combination of Permutation Technique Followed by Encryption,” International Journal of Computer Science and Network Security, Vol. 8, No. 4, 2008, pp. 191-197.
- S. P. Indrakanti and P. S. Avadhani, “Permutation Based Image Encryption Technique,” International Journal of Computer Applications, Vol. 28, No. 8, 2011, pp. 45-47.
- B. Acharya, S. K. Panigrahy, S. K. Patra and G. Panda, “Image Encryption Using Advanced Hill Cipher Algorithm,” International Journal of Recent Trends in Engineering, Vol. 1, No. 1, 2009, pp. 663-667.
- S. S. Mohammad, M. Sattar and A. R. Ebrahimi, “A Novel Image Encryption Algorithm Based on Hash Function,” 6th Iranian Machine Vision and Image Processing (MVIP), Isfahan, 27-28 October 2010, pp. 1-6.
- A. Nag, J. P. Singh, S. Khan, S. Biswas, D. Sarkar and P. P. Sarkar, “Image Encryption Using Affine Transform and XOR Operation,” International Conference on Signal Processing, Communication, Computing and Networking Technologies, Thuckalay, 21-22 July 2011, pp. 309-312.
- I. Ismail, M. Amin and H. Diab, “A Digital Image Encryption Algorithm Based a Composition of Two Chaotic Logistic Map,” International Journal of Network Security, Vol. 11, No. 1, 2010, pp. 1-10.
- S. I. Ibrahim, H. M. Abuhaiba, H. B. Abuthraya and R. A. Hubboub, “Image Encryption Using Chaotic Map and Block Chaining,” International Journal of Computer Network and Information Security, Vol. 4, No. 7, 2012, pp. 19-26.
- K. N. Pareek, “Design and Analysis of a Novel Digital Image Encryption Scheme,” International Journal of Network Security & Its Applications, Vol. 4, No. 2, 2012, pp. 95-108.
- R. Enayatifar and A. H. Abdullah, “Image Security via Genetic Algorithm,” International Conference on Computer and Software Modeling, Vol. 14, 2011, pp. 198- 203.
- Q. Zhang, X. Xue and X. Wei, “A Novel Image Encryption Algorithm Based on DNA Subsequence Operation,” The Scientific World Journal, Vol. 2012, 2012, Article ID 286741. http://dx.doi.org/10.1100/2012/286741
- C. Shannon, “Communication Theory of Secrecy Systems,” Bell System Technical Journal, Vol. 28, No. 4, 1949, pp. 656-715. http://dx.doi.org/10.1002/j.1538-7305.1949.tb00928.x
- G. Chen, Y. Mao and C. Chui, “A Symmetric Image Encryption Scheme Based on 3D Chaotic Cat Maps,” Chaos, Solitons and Fractals, Vol. 21, No. 3, 2004, pp. 749-761. http://dx.doi.org/10.1016/j.chaos.2003.12.022
- H. Liu, Z. Zhu, H. Jiang and B. Wang, “A Novel Image Encryption Algorithm Based on Improved 3D Chaotic Cat Map,” The 9th IEEE International Conference for Young Computer Scientists, Hunan, 18-21 November 2008, pp. 3016-3021.
- Z. Liehuang, L. Wenzhuo, L. Lejian and L. Hong, “A Novel Image Scrambling Algorithm for Digital Watermarking Based on Chaotic Sequences,” International Journal of Computer Science and Network Security, Vol. 6, No. 8B, 2006, pp. 125-130.

