Journal of Applied Mathematics and Physics
Vol.03 No.07(2015), Article ID:57663,7 pages
10.4236/jamp.2015.37102
Optimal Weights in Nonparametric Analysis of Clustered ROC Curve Data
Yougui Wu
Department of Epidemiology and Biostatistics, College of Public Health, University of South Florida, Tampa, Florida, USA
Email: ywu@health.usf.edu


Received 8 May 2015; accepted 23 June 2015; published 30 June 2015

ABSTRACT
In diagnostic trials, clustered data are obtained when several subunits of the same patient are observed. Within-cluster correlations need to be taken into account when analyzing such clustered data. A nonparametric method has been proposed by Obuchowski (1997) to estimate the Receiver Operating Characteristic curve area (AUC) for such clustered data. However, Obuchowski’s estimator gives equal weight to all pairwise rankings within and between cluster. In this paper, we modify Obuchowski’s estimate by allowing weights for the pairwise rankings vary across clusters. We consider the optimal weights for estimating one AUC as well as two AUCs’ difference. Our results in this paper show that the optimal weights depends on not only the within-patient correlation but also the proportion of patients that have both unaffected and affected units. More importantly, we show that the loss of efficiency using equal weight instead of our optimal weights can be severe when there is a large within-cluster correlation and the proportion of patients that have both unaffected and affected units is small.
Keywords:
Diagnostic Test, Optimal Weight, Asymptotic Relative Efficiency, Receiver Operating Characteristic Curve, Area under a ROC Curve

1. Introduction
In diagnostic trials, clustered data are obtained when several subunits of the same patient are observed. For example, in a study by Masaryk et al. (1991) [2], two radiologists evaluated 65 carotid arteries (left and right) in 36 patients using three-dimensional Magnetic Resonance Angiography(MRA), a potential screeening tool for athe- rosclerosis of the carorid arteries. These patients also underwent intra-arterial digital subtraction angiography (DSA), which is considered the gold standard for characterizing the degree of stenosis. The goals of the study were to evaluate the performance of MRA according to each reader, and to compare the performance for the two radiologists.
In the above example, each patient(cluster) contributes a number of unaffected and affected units. Correlation exists for outcomes between two unaffected units, between two affected units, and between an unaffected and an affected unit from the same cluster, and between the outcomes of the two diagnostic tests from the same cluster. All these correlations need to be taken into account when analyzing such clustered data.
An ROC curve is a plot of a diagnostic test’s sensitivity versus 1-specificity. The curve is constructed by changing the cutpoint that defines a positive diagnostic test result. The area under the ROC curve (AUC) summarizes the test’s overall diagnostic ability and is typically used as a global measure of the accuracy of the diagnostic test.
In the clustered data case, Obuchowski (1997) [1] proposed a nonparametric AUC estimator, and derived an asymptotic variance estimate for the AUC estimator, taking into account of within-cluster correlations. However, Obuchowski’s AUC estimator gives equal weight to all pairwise rankings within and between clusters. Clusters can be different in terms of cluster size, the number of unaffected units, and the number of affected units. In the presence of various within-cluster correlations, these differences would affect the contribution of a cluster to the overall variance of the AUC estimator and hence weights should vary across clusters.
In this paper, we modify Obuchowski’s estimator by allowing the weight assigned to each pairwise ranking to vary across clusters, and derive the optimal weights that minimize the variance of the AUC estimator. Our results in this paper show that the optimal weights depends not only on the within-cluster correlation but also the proportion of clusters that have both unaffected and affected units. More importantly, we show that the gain of efficiency in comparison with two simple weighting schemes can be doubled when there is a large within-cluster correlation and the proportion of clusters that have both unaffected and affected units is small.
The rest of this paper is organized as follows. In Section 2, the optimal weights for one AUC are derived and the estimators of the optimal weights are discussed. The relative asymptotic efficiencies in comparing our optimal estimator with two simple weighting schemes are studied. A data example is presented in Section 3 and conclusions are provided in Section 4.
2. Optimal Weights for Estimating One Auc
2.1. Optimal Weights Derivation
Assume that there are  clusters, of which
clusters, of which 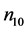 clusters contain only unaffected units,
clusters contain only unaffected units, 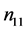 clusters contain both unaffected and affected units, and
clusters contain both unaffected and affected units, and 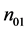 clusters contain only affected units. The total number of clusters with at least one unaffected unit is given by
clusters contain only affected units. The total number of clusters with at least one unaffected unit is given by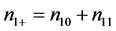 , and the total number of clusters with at least one affected unit is given by
, and the total number of clusters with at least one affected unit is given by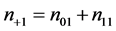 . Without loss of generality, we assume that clusters
. Without loss of generality, we assume that clusters 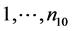 contain
contain
only unaffected units, clusters 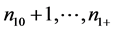 contain both unaffected and affected units, and clusters
contain both unaffected and affected units, and clusters 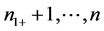 contain only affected units. Let
contain only affected units. Let 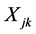 denote the diagnostic test result of the kth unaffected unit in the jth cluster
denote the diagnostic test result of the kth unaffected unit in the jth cluster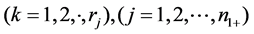 . Similarly, let
. Similarly, let 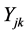 denote the diagnostic test result of the kth affected unit in the jth cluster
denote the diagnostic test result of the kth affected unit in the jth cluster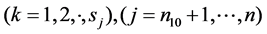 .
.
Let 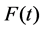 and
and 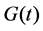 be the distribution functions of
be the distribution functions of 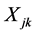 and
and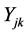 , respectively. Assume that if the value of
, respectively. Assume that if the value of 





where 

Note that 

where 




where 




We propose to estimate 

Notice that when 

To derive our optimal weight, we utilize the following result which can be found in the Appendix of Emir, et al. (2000) [3]:

where
and 



Note that
and
Defining the transformation

we can express the variance of 



where
and
The optimal weights can be obtained by minimizing (8) with respect to 





and

where
and
2.2. Asymptotic Variance Comparison
Let 






Along the same line of the proofs for (??), (??) and (??), we can show that 






and

where
and
Let 













Figure 1. The effect of 



3. Conculsions
We have proposed an optimal nonparametric estimator for one AUC, which modifies Obuchowski’s estimate by allowing different weights for the pairwise rankings within and between cluster. Optimal weights for one AUC has been derived by minimizing the variance of the estimate of one AUC(two AUCs’ difference). Asymptotic performance of the AUC estimate using our optimal weights has been studied in contrast with the two weighting schemes.
We have shown that when there is a moderate within-cluster unaffected-affected units correlation and the proportion of clusters that contain both unaffected and affected units is small, using either of the two weighting schemes, corresponding to Obuchowski’s estimator or the estimator with equal cluster weights, can lead to dramatic efficiency loss. For this situation, the optimal weights are recommended.
Cite this paper
Yougui Wu, (2015) Optimal Weights in Nonparametric Analysis of Clustered ROC Curve Data. Journal of Applied Mathematics and Physics,03,828-834. doi: 10.4236/jamp.2015.37102
References
- 1. Masaryk, A.M., Ross, J.S., DiCello, M.C., Modic, M.T., Paranandi, L. and Masaryk, T.J. (1991) 3DFT MR Angiography of the Carotid Bifurcation: Potential and Limitations as a Screening Examination. Radiology, 179, 797-804. http://dx.doi.org/10.1148/radiology.179.3.2027995
- 2. Inaba, Y., Arai, Y., Kanematsu, M., Takeuchi, Y., Matsueda, K., Yasui, K., Hoshi, H. and Itai, Y. (2000) Revealing Hepatic Metastases from Colorectal Cancer: Value of Combined Helical CT during Arterial Portography and CT Hepatic Arteriography with a Unified CT and Angiography System. American Journal of Roentgenology, 174, 955-961. http://dx.doi.org/10.2214/ajr.174.4.1740955
- 3. DeLong, E.R., DeLong, D.M. and Clarke-Pearson, D.L. (1988) Comparing the Areas under Two or More Correlated Receiver Operating Characteristic Curves: A Nonparametric Approach. Biometrics, 44, 837-845. http://dx.doi.org/10.2307/2531595
- 4. Obuchowski, N.A. (1997) Nonparametric Analysis of Clustered ROC Curve Data. Biometrics, 53, 567-578. http://dx.doi.org/10.2307/2533958
- 5. Emir, B., Wieand, S., Su, J. and Cha, S. (1998) Analysis of Repeated Markers Used to Predict Progression of Cancer. Statistics in Medicine, 17, 2563-2578. http://dx.doi.org/10.1002/(SICI)1097-0258(19981130)17:22<2563::AID-SIM952>3.0.CO;2-O
- 6. Emir, B., Wieand, S., Jung, S. and Ying, Z. (2000) Comparison of Diagnostic Markers with Repeated Measurements: A Non-Parametric ROC Curve Approach. Statistics in Medicine, 19, 511-523. http://dx.doi.org/10.1002/(SICI)1097-0258(20000229)19:4<511::AID-SIM353>3.0.CO;2-3






















