ABSTRACT

The present paper is devoted to a novel smoothing function method for convex quadratic programming problem with mixed constrains, which has important application in mechanics and engineering science. The problem is reformulated as a system of non-smooth equations, and then a smoothing function for the system of non-smooth equations is proposed. The condition of convergences of this iteration algorithm is given. Theory analysis and primary numerical results illustrate that this method is feasible and effective.

Keywords:Fixed-Point Iteration; Convex Quadratic Programming Problem; Convergence; Smoothing Function

1. Introduction

Consider the following convex quadratic programming problem

(1)

where  is an symmetrical positive semi-definite partitioned matrix,  is an  partitioned matrix, and 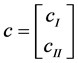 are vectors in  and , respectively. And ,

are the partitioned matrix of  and  respectively.

As is well known, this problem models a large spectrum of applications in computer science. Operation research and engineering as the nonlinear programming is solved eventually based on the convex quadratic programming problem. Therefore, the study on its effective solvers becomes a prolonged research subject.

Common effective algorithm is proposed related to certain schemes of convex quadratic programming problem, see [1-5]. Moreover, these methods are not polynomial algorithm in [6]. And the theory and algorithm of quadratic programming are presented completely. According to the optimization condition (KKT) and the duality theory of quadratic programming, the fixed-point iteration method is obtained for equality constrained (see [7]) and inequality constrained (see [8]) convex quadratic programming problem respectively. In fact, equality and inequality can be converted with inputting artificial variables and slack variables. The main default is to increase the scale and numerical difficulty while introduces these variables. Motivated by smoothing methods of

[9-11] and fixed-point method of [7,8], the paper mainly concerns about the mixed constraint quadratic programming and the fixed-point iteration method is given. And also the rank of the coefficient matrix is not full. The method considering is fulfilled efficiently. Thus the proposing question in [8] is solved.

2. Scheme of Algorithm

According to the dual theory, the dual problem of primal problem (1) is

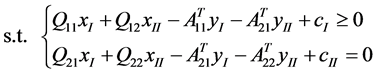(2)

where.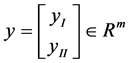

Let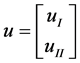, , , 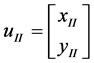we know if is the optimal solution of (1),there exists a vector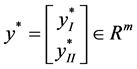, an symmetrical positive semi-definite partitioned matrix, and 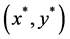 is the optimal solution of (2).

Let us define the following notation

is the optimal solution of (1) and 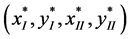is the optimal solution of (2) }.

It is easy to verify that  is a close set.

Suppose that the feasible region is not empty. A necessary and sufficient condition for a optimal solution is that:

1) Primal feasibility

2) Dual feasibility

3) Complementary condition

The scheme are rewritten below

(3)

Where

More formally, the following link fixed-point iteration problem is performed

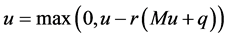(4)

The component form is

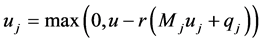(5)

Where.

The question (5) is non-smooth optimization problem, and the Newton-type methods cannot be applied directly. In the paper, we converted the problem into a smooth optimization.

At the beginning, we introduce a function mapping  into , and have the following properties.

Property 1 Let 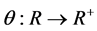 be a real function, and such that:

1) 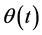is strictly convex and differentiable;

2);

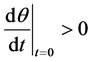3);

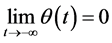4)

We assumed that 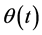is a convex and differentiable function, which indicate one can apply the classical Newton-type algorithm directly. And the assumption means that 0 is not a sub-gradient of at 0. The hypothesis (3) and (4) indicate the approximate function has the same numerical properties as the max-function.

We consider the following function, and describe as above

(6)

For any , satisfies the following properties:

Theorem 1 Let be a function given as (6), then for any arbitrary , is strictly convex and differentiable, and we have .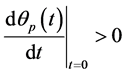

Proof According to property 1 and (6), the convexity and differentiability are straightforward.

Nothing that

The property (2) implies .

Theorem 2 Let  be a function given as (6), then . That is, the function  uniformly converges to the max-function, when the adjustable parameter approaches.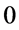

Proof For 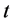fixed, we can compute

If , then ; otherwise, change variable,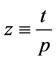

Hence,  for all.

From the discussion above, we introduce the following function in the paper

and

It is easily known that satisfies the properties (1) to (4), together with theorem 1 and 2. Thus, the max-function in (3) replaced by , and the fixed-point iteration which basing on smoothing function is obtained.

Algorithm

Step 1 Set a initial point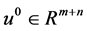, choose , , 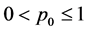, let;

Step 2 Apply fixed-point algorithms to solve

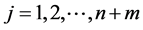(7)

Step 3 Terminal condition: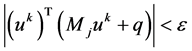, stop; otherwise, go to Step 4;

Step 4 Let ,, go to step 2.

The Jacobian matrix in (7) is shown

(8)

Where

3. Convergence Analyses

Now we discuss the convergence of the algorithm. To begin with, two simple lemmas are introduced that is the basis of our theoretical analysis. Since their proof can be found in reference [12], we here omit the proof due to space.

Lemma 1 [12] A necessary and sufficient condition for the fixed-point iteration method to be convergent is that the spectral radius of Jacobian matrix B satisfies 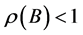, where the spectral radius  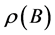be defined as

, and denotes the eigenvalue of matrix .

Lemma 2 [12] Suppose is a matrix, whose eigenvalues can be ordered from the smallest to largest, i.e. 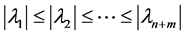, and V is diagonal matrix with nonnegative diagonal elements, then the maximum norm of the matrix ’s eigenvalue such that.

Theorem 3 suppose 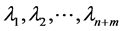 be the eigenvalues of the Jacobian matrix, if one of the following conditions is true, then we can select the proper parameter 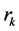 makes the algorithm convergent:

(1) The real part of is positive, that is ;

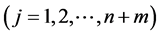(2) All of the eigenvalues of matrix 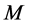are real.

Proof Suppose are eigenvalues of the Jacobian matrix in (8), and matrix eigenvalues denote as .

Let  (where ).

Note that

If , for all positive number of; while , we know .

1) If is positive, we let, and have

;

2) If all of the eigenvalues of matrix are real, we let , and have .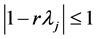

For all discussed above, associate with Lemma 1, we know that the matrix has the eigenvalues of , such that

According to the theorem above, the algorithm is always convergent if the parameter is chosen properly. Thus the recent relevant results in reference [8] are extended.

4. Numerical Experiment and Conclusion

In this section, we implement algorithm for solving system of inequalities in MATLAB7.0 in order to demonstrate the behavior of the algorithm. Due to page limit, we omit to test the effectiveness of our method in generating highly quadratic programming problems.

Example 1 Consider

The exact optimal solution is 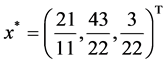, and the optimal value of objective function is .

Example 2 Consider

The exact optimal solution is 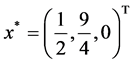, and the optimal value of objective function is .

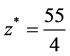The results are shown in Table1

From the table, we can see that the algorithm is very simple and only applies the traditional fixed-point method. The implementation of this algorithm is rather easy.

Example 3 Consider

And

The exact optimal solution is

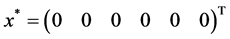and the optimal value of objective function is .

Appling the method proposed, the iterations consuming time are shown in Table2

Acknowledgements

This work is supported by the Beijing Municipal Commission of Education Science and Technology Program (KM201310017006) and the Beijing URT Program (2012J00018).

REFERENCES