ABSTRACT

By exponentiating each of the components of a finite mixture of two exponential components model by a positive parameter, several shapes of hazard rate functions are obtained. Maximum likelihood and Bayes methods, based on square error loss function and objective prior, are used to obtain estimators based on balanced square error loss function for the parameters, survival and hazard rate functions of a mixture of two exponentiated exponential components model. Approximate interval estimators of the parameters of the model are obtained.

1. Introduction

The study of homogeneous populations was the main concern of statisticians along history. However, Newcomb [1] and Pearson [2] were two pioneers who approached heterogeneous populations with 'finite mixture distributions’.

With the advent of computing facilities, the study of heterogeneous populations, which is the case with many real World populations (see Titterington et al. [3]), attracted the interest of several researchers during the last sixty years. Monographs and books by Everitt and Hand [4], Titterington et al. [3], McLachlan and Basford [5], Lindsay [6] and McLachlan and Peel [7], collected and organized the research done in this period, analyzed data and gave examples of possible practical applications in different areas. Reliability and hazard based on finite mixture models were surveyed by AL-Hussaini and Sultan [8].

In this paper, concentration will be on the study of a finite mixture of two exponentiated exponential components. Due to the exponentiation of each component by a positive parameter, the model is so flexible that it shows different shapes of hazard rate function.

Maximum likelihood estimates (MLEs) and Bayes estimates (BEs), using square error loss (SEL) function are obtained and used in finding the estimates of the parameters, survival function (SF) and hazard rate function (HRF) using the balanced square error loss (BSEL) function.

Approximate interval estimators of the parameters are obtained by first finding the approximate Fisher information matrix.

The cumulative distribution function (CDF), denoted by, of a finite mixture of k components, denoted by, is given by

, (1)

where, for, the mixing proportions

and. The vector of parameters

, where is a parameter space.

The case, in (1), is of practical importance and so,we shall restrict our study to this case. In such case, the population consists of two sub-populations, mixed with proportions p and. We shall write the CDF of a mixture of two components as

, (2)

where, for is the CDF of the sub-population, and.

AL-Hussaini and Ahmad [9] obtained the information matrix for a mixture of two Inverse Gaussian components. AL-Hussaini and Abd-El-Hakim ([10-12]) studied the failure rate of a finite mixture of two components, one of which is Inverse Gaussian and the other is Weibull. They estimated the parameters of such model and studied the efficiency of schemes of sampling. AL-Hussaini [13] predicted future observables from a mixture of two exponential components. AL-Hussaini [14] obtained Bayesian predictive density function when the population density is a mixture of general components. Other references on finite mixtures may be found in AL-Hussaini and Sultan [8].

In this paper, the components are assumed to be exponentiated exponential whose CDFs are of the form

, (3)

where So that the corresponding probability density function (PDF) components take, for, the form

. (4)

The PDF, SF and HRF, of the mixture (2), denoted by and are given by

, (5)

(6)

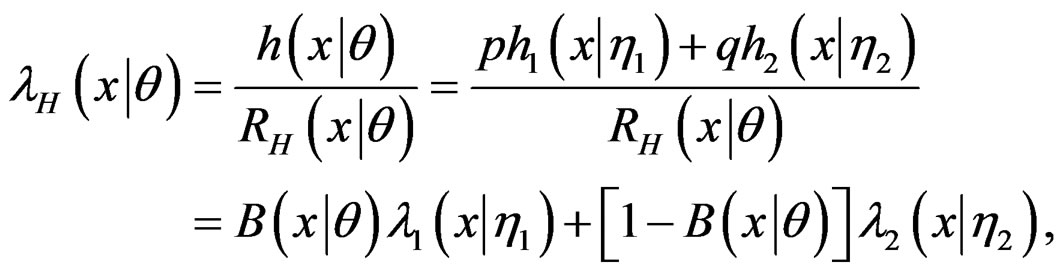(7)

where, and for,

. (8)

In (5)-(8), and shall be given by (3) and (4), respectively, so that

2. Hazard Rate Function of the Mixture

It is well-known that the exponential distribution has a constant HRF on the positive half of the real line. A finite mixture of two exponential components has a decreasing hazard rate function (DHRF) on the positive half of the real line. See, for example, AL-Hussaini and Sultan [8]. If each of the exponential components is exponentiated by a positive parameter, more flexible model is obtained in that several shapes of the HRF of the mixture are obtained. Figure 1 shows six different shapes of CDFs and their corresponding HRFs of the vector of parameters. Examples of such shapes are given as follows:

3. Point Estimation Using Balanced Square Error Loss Function

It is well-known that the Bayes estimator of a function of a vector of parameters under SEL is given by

(9)

where the integrals are taken over the m-dimensional space and is the posterior PDF of give.

The SEL function has probably been the most popular loss function used in literature. The symmetric nature of SEL function gives equal weight to overand under-estimation of the parameters under consideration. However, in life-testing, over-estimation may be more serious than under-estimation or vice-versa. Consequently, research has been directed towards asymmetric loss functions. Varian [15] suggested the use of linear exponential (LINEX) loss functions. Thompson and Basu [16] suggested the use of quadratic exponential (QUADREX) loss function. Ahmadi et al. [17] suggested the use of the so called balanced loss function (BLF), which was originated by Zellner [18], to be of the form

(10)

where is am arbitrary loss function, is a chosen “target” estimator of and the weight

The BLF (10) specializes to various choices of loss functions such as the absolute error loss, entropy, LINEX and generalizes SEL functions.

If is substituted in (10), we obtain the balanced square error loss (BSEL) function, given by

The estimator of a function, using BSEL may be given by

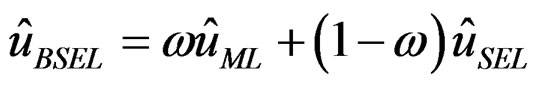, (11)

where is the MLE of and 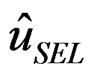its Bayes

estimator using SEL function. The estimator of a function, using BSEL is actually a mixture of the MLE of the function and the BE, using SEL. Other estimators, such as the least squares estimator may replace the MLE. Also, a LINEX or QUADREX loss function could be used for. Having obtained the MLE and BE based on SEL, the estimates based on BSEL function are given, from (11), by

(12)

Suppose that r units have failed during the interval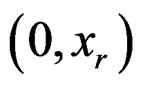: units from the first sub-population and units from the second such that and n – r units , which cannot be identified as to sub-population, are still functioning. Let, for and denote the failure time of the ith unit belonging to the sub-population and that. The likelihood function (LF) is given by Mendenhall and Hader [19], as

(13)

where is the vector of parameters involved and,. By substituting, given by (4), in (13), we obtain

(14)

3.1. Maximum Likelihood Estimation

The log-LF is given by

(15)

The MLEs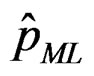, , , , , of the five parameters are obtained by solving the following system of likelihood equations

where

.

The invariance property of MLEs enables us to obtain the MLEs and by replacing the parameters by their MLEs in and.

Remarks 1) If n = r (complete sample case),

,

,

.

2) It can be numerically shown that the vector of parameters, satisfying the likelihood equations actually maximizes the LF (14). This is done by applying Theorem (7-9) on p. 152 of Apostol [20].

3) The parameters of the components are assumed to be distinct, so that the mixture is identifiable. For the concept of identifiability of finite mixtures and examples, see Everitt and Hand [4], AL-Hussainiand Ahmad [21] and Ahmad and AL-Hussaini [22].

3.2. Bayes Estimation Using SEL Function

Suppose that an objective (non-informative) prior is used, in which p, , , , are independent and that p-Uniform on, so that the prior PDF is given by

. (16)

The following theorem gives expressions for the Bayes estimators using the SEL function.

Theorem The Bayes estimators of the parameters, SF and HRF, assuming that the prior belief of the expeimenter has PDF (16), are given by

where

(17)

(18)

(19)

(20)

(21)

,

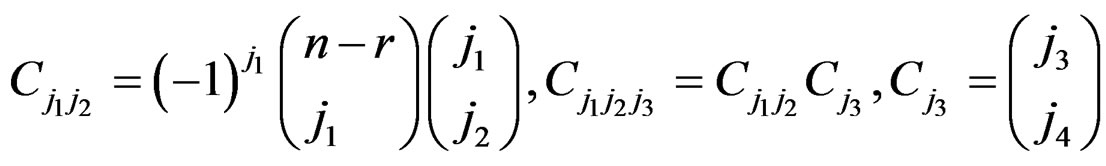is the standard beta function,

, (22)

, (23)

, (24)

, (25)

, (26)

(27)

, (28)

, (29)

, (30)

(31)

(32)

(33)

The proof of the theorem is given in Appendix 1.

4. Approximate Confidence Intervals

Let. The observed Fisher information matrix F (see Nelson [23]), for the MLEs of the parameters is the 5 × 5 symmetric matrix of the negative second partial derivatives of log-LF (15) with respect to the parameters. That is

, evaluated at the vector of MLEs.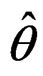

The second partial derivatives are given in Appendix 2.

The inverse of F is the local estimate V of the asymptotic variance-covariance matrix of

. That is,

, (34)

where.

The observed Fisher information matrix enables us to construct confidence intervals for the parameters based on the limiting normal distribution. Following the general asymptotic theory of MLEs, the sampling distribution of, can be approximated by a standard normal distribution, where , the ith diagonal element of the matrix V, given by (34).

An approximate two-sided confidence interval for, is given for, by

, (35)

where is the percentile of the standard normal distribution with right—tale probability of c.

5. Numerical Example

5.1. Point Estimation of the Parameters, SF and HRF

A sample is generated from the mixture in such a way that. We generate 100 samples of size n = 50 each, from a finite mixture of two exponentiated exponential components, whose PDF is given by (5) and (4), as follows:

1) Generate and from Uniform (0,l) distribution.

2) For given values of p, a₁, a₂, b₁, b₂, generate x according to the expression:

An observation belongs to sub-population 1, if and to sub-population 2, if, where the sample is generated from the mixture in such a way that.

3) Repeat until you get a sample of size n.

The observations are ordered and only the first r = 45 (90% of n) out of the n = 50 observations are assumed to be known. Now we have observations from the first component of the mixture and observations from the second component ().

The value of is chosen to be equal to 1.

The estimates of p, a₁, a₂, b₁, b₂, and and absolute biases are computed by using the ML and Bayes methods. The Bayes estimates are obtained under SEL function. An estimator of a function, using BSEL, is actually a mixture (w = 0.2, 0.4, 0.6, 0.8) of the MLE of the function and the BE, using SEL.

The MLEs are computed using the built-in MATLAB^® function “ga” to find the maximum of the log-LF (15) using the genetic algorithm. This is better than solving the system of five likelihood equations in the five unknowns, by using some iteration scheme. Neverthless,

the system is needed for the computations of the asymptotic variance-covariance matrix.

The (arbitrarily) chosen actual population values are  p = 0.4, a₁ = 2, a₂ = 3, b₁ = 2, and b₂ = 3. For, the actual values for and are given, respectively, by 0.1862 and 2.3096.

The estimates of the parameters, SF and HRF under the BSEL function are given in Table 1, for different weights. It may be noticed that when, we obtain the MLEs while the case, yields the Bayes estimates under SEL(B-SEL) function.

5.2. Interval Estimation of the Parameters

The asymptotic variance-covariance matrix (34), based on the generated data, is found to be

So that the asymptotic variances of the estimators of the parameters are given by:

It then follows that the approximate 95% confidence intervals of the parameters p, , , and, given by (35), are given, respectively, by: (0.271 < p < 0.561), (0.5287 < a₁ < 4.7599), (1.3832 < a₂ < 5.3226), (0.9294 < b₁ < 4.18) and (1.8039 < b₂ < 4.56).

6. Concluding Remarks

In this article, we have considered point and interval estimation. Point estimation, of the parameters of a finite mixture of two exponentiated exponential components, SF and HRF is based on BLEF which is a weighted average of two losses: one of which reflects precision of estimation and the other reflects goodness-of-fit. This asymmetric loss function may be considered as a compromise between Bayesian and non-Bayesian estimates. We have also estimated the parameters of the mixture by obtaining the asymptotic variance-covariance matrix and hence the approximate confidence intervals.

REFERENCES

Appendix 1

Proof of the Theorem By expanding the last term in LF (14), using the binomial expansion, it can be seen that

where.

So that LF (14) can be written in the form

where, , are given by (31). Suppose that the prior PDF is as in (16). It then follows that the posterior PDF is given by

(34)

where and are given by (32). The normalizing constant A is given by

where is given by (17), in which is given by (22).

Applying (9) when

their Bayes estimates using SEL function are given by

, is given in (17).

, is given in (18), in which is given by (23)., is given in (18), in which is given by (24).

, is given in (19), in which is given by (25).

, is given in (19), in which is given by (26).

is given in (20), in which is given by (27) and by (28).

where

.

Since p ≤ 1, then

so that

where. It then follows that

By substituting, for, and using given by (34), it can be shown that

(35)

where are given by (33). By integrating both sides of (35) with respect to the five parameters, we obtain

where S₇ is given by (21), in which I₇ is given by (29)

and I₈ by (30).

Appendix 2

Second Partial Derivatives of the Log-likelihood Function

,

,

,

,

,

,

,

,

,

,

,

,

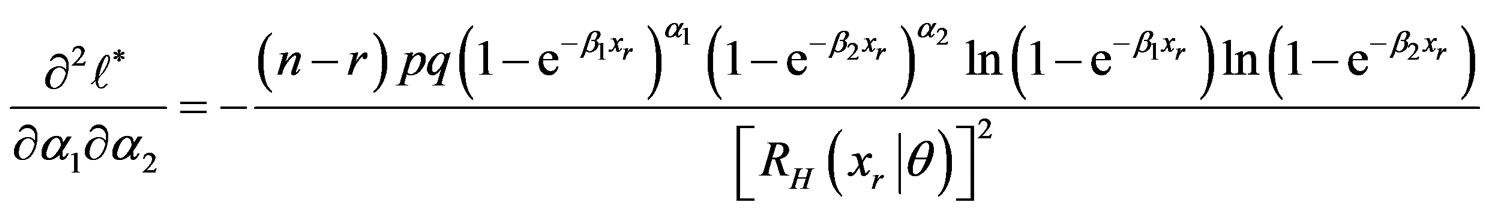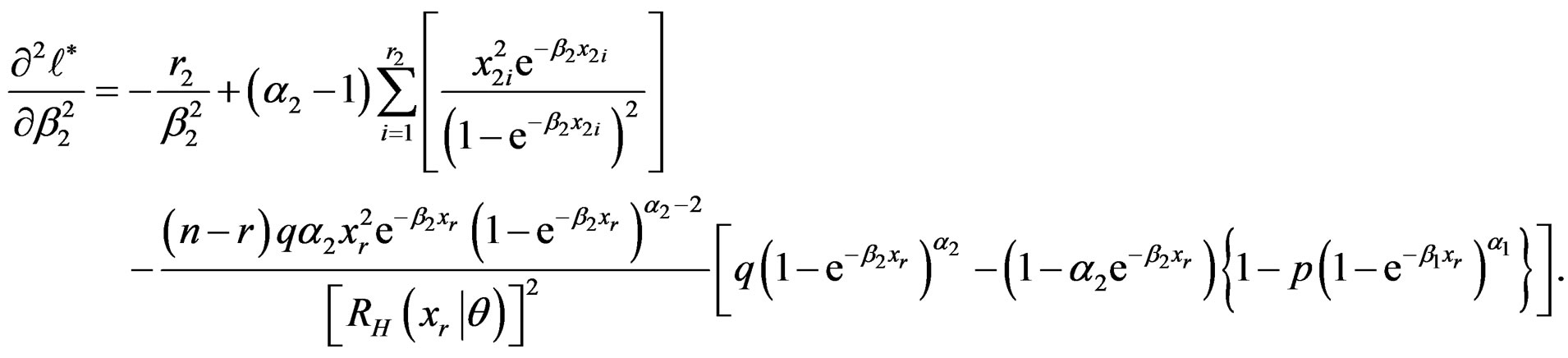
NOTES

^*Corresponding author.