Smart Grid and Renewable Energy
Vol.07 No.06(2016), Article ID:67841,19 pages
10.4236/sgre.2016.76016
Performance Study of a Self-Excitation Dual Stator Winding Induction Generator for Renewable Distributed Generation Systems
Faris Hamoud, Mamadou Lamine Doumbia, Ahmed Cheriti
Department of Electrical and Computer Engineering, Université du Québec à Trois-Rivières, Québec, Canada

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 May 2016; accepted 26 June 2016; published 29 June 2016
ABSTRACT
Renewable power generation is a suitable technology used to deliver energy locally to customers especially in remote regions. Wind energy based on induction generator situates in a foreground position in the total energy produced using renewable sources. In the last few decades, a new self- excitation generator was based on multi-stator induction strongly emerges. This article presents a systematic modelling, a detailed analysis and the performance analysis of self-excitation dual stator winding induction generator (SE-DSWIG). The modelling of the SE-DSWIG was done with taking in account the common mutual leakage inductance between stators and the magnetizing inductance, which played a principal role in the stabilization of the output voltage in the steady state. The generator feeds the end user emulated by an inductive-resistive load. In order to simulate the weather conditions’ variation, a step change of the prime mover speed was applied on the SE- DSWIG. A passive series and shunt compensator was used to mitigate the voltage sag and swell appeared in the power system due to wind variation and the lack of reactive power consumed by the inductive load.
Keywords:
Magnetizing Inductance, Magnetizing Current, Voltage Mitigation, Self-Excitation, Passive Compensator

1. Introduction
Nowadays, distributed generation systems (DGs) impose themselves as an attractive research area. According to a study done by the Electric Power Research Institute (EPRI), the distributed generation systems participated with 25% in the energy production by the end of 2010 [1] . DGs can be defined as small-scale power generation systems below 50 MW, installed near to the domestic and the industrial customers [2] . This approach gives the possibility to electrify the end users without investing money to enlarge the interconnection network or to implement new big power plants, particularly in remote areas. Eventually, wind, solar, hydro and others kind of renewable energy sources are potential candidates that can play the role of the main energy feeder [3] . This paper is devoted to the wind power generation, which occupies a forefront position in the total energy delivered, especially with the power electronics converters emerging and power management algorithms development [4] [5] . Power generation constitutes of a prime mover (wind turbine), generator, power electronic converter and a coupling transformer [6] . Among generators used in wind power, the self-excitation induction generator is widely used in large scale due to its advantages such as the robustness and low cost of maintenance [7] - [9] .
In the last century, a new generation of self-excitation induction machine strongly emerged in AC applications. It constitutes of multi-stators topology. A self-excitation dual stator windings induction generator (SE- DSWIG) belongs to this category and it brings a lot of advantages compared to the traditional three-phase induction generator such as the minimization of rotor losses and torque ripples, the reduction of harmonic, reducing current without increasing voltage in each phase and the power segmentation [10] . There are two types of SE-DSWIG. The first one is the aim of this work. It contains two identical sets of three-phase windings. Each set represents a stator. This machine allows building several topologies. In the first topology, it could be connected to the grid through a stator and the second one fed a load. In the second topology, both of stators are connected to the grid or fed loads. Another topology consists of a “power stator” and a “control stator”. The first one supplies the end users and the second stator is used to control the reactive power and to maintain the output voltage of the power stator at an acceptable level [11] . These features give the SE-DSWIG the property of unifying the reactive power in both of stators, which participate in the improvement of the delivered power’s quality [12] .
The main drawback of the self-excitation induction generator in distributed generation energy systems is the terminal voltage poor stability [10] . A compensator installed at the Point of common coupling (PCC) is necessary to maintain the voltage at an acceptable level. Generally, the compensator could be the capacity bank that should be designed depending on the prime mover speed and the load size [12] . A static compensator is more suitable for this case but a passive filter has to be inserted between the compensator and grid to protect the end users against harmonics [13] .
In this sense, due to its topologies, the self-excitation dual stator windings induction generator can play both of the roles of power generation and maintain the PCC voltage at an optimal level. The first stator produces voltage and the second connected to a compensator that can inject the reactive power necessary to maintain the output voltage of the first stator. The harmonics generated by the second stator cannot propagate to the first one because there is no physical link between both of stators.
A literature survey on the SE-DSWIG utilisation leads to conclude that it is still in the first steps for the wind power generation. However, it is remarkable that it made important strides in the high-speed AC-application for the airborne, ships and vehicles that need self-power support. In [14] , authors propose a new algorithm to analyse the performance of the SE-DSWIG in term of its characteristics such as prime mover speed, excitation capacitance and so on. In [15] , authors investigated the possibility of supplying several insensitive loads to the frequency variation in airborne. They propose a control technique based on an improved instantaneous slip frequency control strategy that allows feeding inductive and capacitive loads at the same time. In [16] [17] , authors cited the improvement brings from the use of the SE-DSWIG comparing to the conventional three-phase induction generator. In [18] [19] , authors study the possibility of using SE-DSWIG in the high-speed application for offshore energy production in ships.
It is remarkable in former works, that the SE-DSWIG performance was explored in high and enough constant speed to generate power that means it was not exposed to the critical condition in term of speed and power issues. While in speed variation applications such as wind power, it is necessary to use several topologies of inverters and compensators to sustain the power quality and to mitigate issues that appear in variable speed AC application such as voltage collapse, sag, and swell.
This article deals with voltage collapse, sag, and swell issues. For that, a systematic modeling, a detailed analysis and the performance study of SE-DSWIG in stand-alone operating mode are presented. The end user is modeled by an inductive-resistive load. A step variation of the prime mover speed is applied to the generator to emulate the wind speed variation in order to illustrate its influence on SE-DSWIG behavior. A passive compensator is used to mitigate the voltage sag and swell caused by the insertion of the inductive load and due to the prime mover speed variation. The article starts by an introduction that contains the state of the art on the SE-DSWIG, then in section two, the passive shunt and series compensator operation mode are discussed. In the third section, the mathematical modeling of the SE-DSWIG is presented, in addition to the equating of self- excitation capacity bank systems connected in shunt to the generator terminals to get the reactive power necessary for starting. The fourth section contains also the mathematical modeling of the end user represented by an inductive-resistive load with the modeling of passive shunt compensator connected in series and in parallel. In the fifth section, numerical are performed and results are displayed for the SE-DSWIG operation in different operating modes. Then, a conclusion summarises our work and presents the unforeseen challenges.
2. Passive Compensator
The passive compensator is a mature technique that been used since the beginning of the use of electricity [20] [21] . It based on the lossless reactive components such as inductances and capacitances and they are inserted in the grid to solve different power issues related to the voltage and current, such as flickers, losses and harmonics [21] . In addition, they enhance the capacity of energy transfer and power evolution in transient and steady states. The passive compensator could be connected to the grid in series or in parallel. For the parallel passive compensator, its main function based on the exchange of reactive power with the grid through a reactive current to control voltage and power factor at the point of common coupling [22] . While the series passive compensator intervention based on the exchange of a reactive power with the grid through the generation of a series voltage in the same frequency of AC mains [22] . In this work, the passive compensator was designed and connected in series in the first case and in parallel in the second case between the SE-DSWIG terminals and the inductive load (Figure 1). The main function of the passive compensator is to sustain the generator output voltage at an acceptable level and to compensate the reactive power consumed by the load. Figure 2 presents the phasor diagram of the voltage regulation at the point of common coupling (PCC) for the series and the parallel compensator [22] . It illustrates that the series compensator adjusts the injected voltage 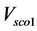 until getting almost the equality between the voltage terminal of the SE-DSWIG
until getting almost the equality between the voltage terminal of the SE-DSWIG 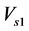 and the voltage terminal of load
and the voltage terminal of load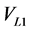 .While in the case of parallel compensator its intervention happens by adjusting reactive current
.While in the case of parallel compensator its intervention happens by adjusting reactive current 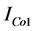 until reaching the desired response.
until reaching the desired response.

Figure 1. Single phase of the generator feeding the inductive load at the presence of passive compensator. (a) Series compensator; (b) Parallel compensator.

Figure 2. Phasor diagram of the voltage regulation at the point of common coupling. (a) Series compensator; (b) Parallel compensator.
3. Mathematical Modelling of SE-DSWIG
Figure 3 illustrates the SE-DSWIG schema. It contains a dual three phase windings sets and a squirrel cage rotor ( ). The first three phase windings set referred (
). The first three phase windings set referred (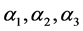 ) and noted stator I while the second three phase windings set denoted (
) and noted stator I while the second three phase windings set denoted ( ) and called stator II. Both of stators are shifted between each other by an angle
) and called stator II. Both of stators are shifted between each other by an angle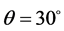 . The rotor is budged by
. The rotor is budged by  against the first stator and by
against the first stator and by 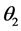 against the second one [23] . All stators and rotor windings are scattered uniformly and every identical three windings set are shifted between them by 120˚.
against the second one [23] . All stators and rotor windings are scattered uniformly and every identical three windings set are shifted between them by 120˚.
The direct-quadratic synchronous referential frame representation of the dual stator windings induction generator is proposed in Figure 4 [23] .
3.1. SE-DSWIG Modelling
The schema shown in Figure 4 can be represented in the equation form by the following voltage expressions [23] [24] :
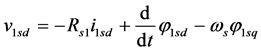 (1)
(1)
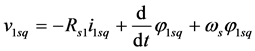 (2)
(2)
Figure 3. Dual stator windings induction generator schema.
Figure 4. SE-DSWIG representation in dq-synchronous referential frame [23] .




The flux linkage of both stators and rotor in (dq)-axis are given by the following equations [16] :











L is the dynamic inductance.



And it defined by the following nonlinear expression [16]



The magnetizing current is calculated by the next expression [24] :

The electromagnetic torque is estimated by the afterward expression [10] :

3.2. DSWIG Self-Excitation Capacity Bank System Modelling
The SE-DSWIG belongs to the self-excitation machines category. It needs a capacity bank connected at the stator terminals to get the necessary reactive power to start working.
At the presence of the residual magnetism and a sufficient rotating speed, the SE-DSWIG engenders enough current that stimulates the self-excitation capacity bank to generate reactive power into the windings. This operation will be repeated until arrivingat an equality between the SE-DSWIG output voltage and capacity bank terminal voltage. This will be the DSWIG operating point.
The following equation represents the excitation capacity bank modeled by the voltage and current relationship equations at the machine’s terminals [24] .

3.3. Modelling of Loads
The nd user is modeled by an inductive load in order to evaluate its influence on the main power supplier performance which is the SE-DSWIG. The end user is represented by the following system of equations:




The direct and quadratic load currents for both of stators are:




with

4. Modelling and Design of the Passive Compensator
The wind speed variation and the presence of loads connected across the stators terminalsprovoke voltage disturbance, especially with poor voltage regulation feature that characterises induction generator. This situation requires the use of a compensator to fix the trouble.
In this work, we deal with a parallel passive compensator represented by a capacity bankconnected in parallel with SE-DSWIG terminals and a series passive compensator connected in series with SE-DSWIG terminals. Both of case are used to sustain the power quality and to mitigate issues that appear in the power system.
4.1. Power System Equations at the Presence of the Series Passive Compensator
The current and voltage equations of the power system in DQ-frame at the presence of the series passive compensator are given as following:
First stator






Second stator










4.2. Power System Equations at the Presence of the Parallel Passive Compensator
The current and voltage equations of the power system in dq-frame at the presence of the series passive compensator are given as following:
First stator




Second stator










injected by the parallel passive compensator to adjust the voltage at the point of common coupling. Figure 5 shows the proposed power system represented by an SE-DSWIG feeds loads through both of stators. A passive compensator was inserted in series in the first scenario and in parallel in the second scenario between the generator and loads to sustain the power quality. The series passive compensator intervention happens by inducing a series voltage in the grid. The parallel one injects a reactive current into the grid to compensate the trouble accurs in the grid as displayed in Figure 2.
5. Numerical Results Analysis
In this section, we present the performance of SE-DSWIG in different situation such as prime mover speed variation, custom load variation, etc. The simulation of this work has been built up in Matlab®/Sim Power Systems. Note that, the simulation of SE-DSWIG is very difficult due to the complexity of its equations. These are
Figure 5. Proposed power system.
constituted of ten differential equations with periodic and variable coefficients and took into account the magnetizing inductance. The passive compensator performance was evaluated. The parameters used in this simulation study are presented in Table 1 and Table 2. The simulation results are detailed below.
5.1. SE-DSWIG Features at No-Load Operation
Figure 6 illustrates that the magnetizing current evolves exponentially with time until reaching the saturation state value that equals to 6.7A at t = 2.5 s. Figure 7 shows that magnetizing inductance value decreases versus the augmentation of the magnetizing current following the polynomial equation defined in (18). Figure 8 and Figure 9 display that both of stators develop a current and voltage that increase exponentially with time then they stabilise at the steady state value that equal 2.85 A for the current and 225 V for terminal voltage at t = 2.5 s. Figure 10 shows that the output current and voltage spread with the same frequency but not on the same phase. The current is ahead by 90˚. From Figure 11, we observe that the rotor current is less than the stator current. It evolves exponentially during the transient regime then it stabilises in the steady state at least than 0.2 A.
Figure 6. Magnetizing current evolution.
Table 1. Investigated system parameters.
Table 2. Nomenclature.
Figure 7. Magnetizing current versus the magnetizing inductance current evolution.
Figure 8. Stator I terminals voltage and current evolution.
Figure 9. Stator II terminals voltage and current evolution.
5.2. SE-DSWIG Features with Inductive-Resistive Load
In this case, inductive-resistive loads are connected with the terminals of stators I and II at t = 3 s. The presence of these loads decreases the output current and voltage of stators due to the lack of reactive power consumed by
Figure 10. Stator terminals voltage and current in zoom.
Figure 11. Rotor current evolution.
the loads (Figures 12-20). At t = 4 s, a passive compensator is connected in series in the first test and in parallel in the second test the passive compensator consists of a capacity bank switched on between the generator and the loads. The compensator either in series or parallel rectifies the trouble, which is translated by augmentation of the current and voltage at the terminals of stators I and II until reaching the ideal values. The series passive compensator intervention was done by engendering an alternative voltage into the SE-DSWIG terminals as illustrated in Figure 16 without affecting the current values as shown in Figure 13 and Figure 15. Whereas the parallel passive compensator intervention happens by introducing a quadratic current at the terminals that provoke an augmentation in current values after compensation as shown in Figure 18 and Figure 20. This is due to the transfer of reactive power from capacity bank to the power system as a reactive current that justifies the augmentation of current after parallel compensation.
5.3. SE-DSWIG Features with Variation of Speed at the Start-Up
In this case, several speed values are applied to investigate their influence on the SE-DSWIG operation. Figure 21 and Figure 22 show that the current and the voltage evolution are proportional with the augmentation of speed value.
Figure 12. Stator I three-phase voltage.
Figure 13. Stator I three-phase current.
Figure 14. Stator II three-phase voltage.
Figure 15. Stator II three-phase current.
Figure 16. Series compensator engendered voltage.
Figure 17. Stator I three-phase voltage.
Figure 18. Stator I three-phase current.
Figure 19. Stator II three-phase voltage.
Figure 20. Stator II three-phase current.
Figure 21. Stator I voltage magnitude.
Figure 22. Stator I current magnitude.
5.4. SE-DSWIG Features with Variation of Speed in Steady State
In this case, we applied a speed step variation on the prime mover emulating the variation of wind speed in real condition. At t = 3 s, the speed decreases from 314.5 rad/s to 310 rad/s. Figure 23 and Figure 24 illustrate that the diminution of speed provokes a voltage sag but the intervention of passive compensator in series or in parallel at t = 4 s rectifies the trouble and the voltage magnitude backs to the desired value.
In the other case, the prime mover speed changes from 314.5 rad/s to 320 rad/s. This speed variation provokes a voltage swell as shown in Figure 25 and Figure 26. The presence of the compensator at t = 4 s mitigates the voltage.
Voltage sag and swell phenomena are the most influential issue on distributed generation system, especially with wind turbine systems.
6. Conclusion
Wind energy based distribution generation systems occupy forefront position in total energy production using renewable sources. Induction generator based wind systems are widely used because of their advantages. A new self-excitation induction generator consisting of two stators was presented in this work. We started by the mathematical modeling of the SE-DSWIG with taking into account the common mutual leakage inductance between stators and also magnetizing inductance which plays a principal role in the stabilization of the output voltage in the steady state. The SE-DSWIG was studied at no-load and connected to the end user, modeled by an inductive-resistive load. A step variation of the prime mover speed was applied at the SE-DSWIG start-up and
Figure 23. Stator I three-phase voltage.
Figure 24. Stator I voltage magnitude evolution.
Figure 25. Stator I three-phase voltage.
Figure 26. Stator I three-phase voltage.
after reaching saturation. A passive shunt compensator was connected in series in firstly and in parallel secondly between the generator and the end user in order to mitigate the voltage disturbance caused by the presence of load or due to the prime mover speed variation. The SE-DSWIG shows a good performance in different operating modes and gives the opportunity to build several topologies such as feeding two different end users or a stator connected to the grid utility and the other one feeding a particular customer. The compensator supervised perfectly the power system stability and it intervened to mitigate the voltage sag and swell. Nevertheless, the passive compensator needs to be adapted for every intervention, depending on the prime mover speed and the load size. The drawback of this technique is its slowness comparing with the rapidity variation of both of loads size and weather conditions, so new technique is needed to allow better adapting with these requirements. Customer power devices (CPD) and flexible AC transmission system (FACTS) connected in series or in parallel such as D-STATCOM, DVR or hybrid such as UPFC, UPQC are proposed to meet the demands in term of rapidity and efficiency. In addition, the use of an advanced control algorithm is necessary to supervise the function of the active compensators (DVR, D-STATCOM, etc.) that participate in the improvement of the power flow and the mitigation of power quality issues that happen in AC applications.
Cite this paper
Faris Hamoud,Mamadou Lamine Doumbia,Ahmed Cheriti, (2016) Performance Study of a Self-Excitation Dual Stator Winding Induction Generator for Renewable Distributed Generation Systems. Smart Grid and Renewable Energy,07,197-215. doi: 10.4236/sgre.2016.76016
References
- 1. Ackermann, T., Andersson, G. and S?der, L. (2001) Distributed Generation: A Definition. Electric Power Systems Research, 57, 195-204.
http://dx.doi.org/10.1016/S0378-7796(01)00101-8� - 2. Yadav, A. and Srivastava, L. (2014) Optimal Placement of Distributed Generation: An Overview and Key Issues. The IEEE International Conference on Power Signals Control and Computations (EPSCICON), India, 6-11 January 2014, 1-6.
- 3. Borbely, A.-M. and Kreider, J.F. (2001) Distributed Generation: The Power Paradigm for the New Millennium. CRC Press LLC.
http://dx.doi.org/10.1201/9781420042399 - 4. Zhang, X., Cao, X., Wang, W. and Yun, C. (2013) Fault Ride-Through Study of Wind Turbines. Journal of Power and Energy Engineering, 1, 25-29.
http://dx.doi.org/10.4236/jpee.2013.15004 - 5. Wen, Z.-W., Ding, L. and He, S.-E. (2013) Analysis on Effect of Parameters of Different Wind Generator on Power Grid Transient Stability. Energy and Power Engineering, 5, 363-367.
http://dx.doi.org/10.4236/epe.2013.54B070 - 6. Bouzid, A.M., Sicard, P., Cheriti, A., Guerrero, J.M., Bouhamida, M. and Golsorkhi, M.S. (2015) Voltage and Frequency Control of Wind-Powered Islanded Microgrids Based on Induction Generator and STATCOM. The IEEE 3rd International Conference on in Control, Engineering & Information Technology (CEIT), Tlemcen, Algeria, 25-27 May 2015, 1-6.
http://dx.doi.org/10.1109/ceit.2015.7232986 - 7. Singh, G.K., Yadav, K.B. and Saini, R.P. (2007) A Self-Excited Six-Phase Induction Generator for Stand-Alone Renewable Energy Generation. The IEEE International Aegean Conference on in Electrical Machines and Power Electronics, Bodrum, 10-12 September 2007, 690-695.
http://dx.doi.org/10.1109/acemp.2007.4510591 - 8. Nounou, K., Marouani, K., Benbouzid, M. and Tabbache, B. (2014) Six-Phase Induction Machine Operating as a Standalone Self-Excited Induction Generator. The IEEE International Conference on Green Energy, Sfax, Tunisia, 25-27 March 2014, 158-163.
- 9. Elhafyani, M., Zouggar, S., Benkaddour, M. and Aziz, A. (2014) Behavior an Induction Generator without and with a Voltage Regulator. Smart Grid and Renewable Energy, 5, 207-219.
http://dx.doi.org/10.4236/sgre.2014.59020 - 10. Amimeur, H., Aouzellag, D., Abdessemed, R. and Ghedamsi, K. (2012) Sliding Mode Control of a Dual-Stator Induction Generator for Wind Energy Conversion Systems. International Journal of Electrical Power & Energy Systems, 42, 60-70.
http://dx.doi.org/10.1016/j.ijepes.2012.03.024 - 11. Li, Y., Hu, Y., Huang, W., Liu, L., Chen, G.-H. and Qiu, J. (2007) The Dual Stator-Winding Induction Generator for Wide-Speed-Range Operation. The IEEE International Conference on Clean Electrical Power, Capri, 21-23 May 2007, 619-624.
- 12. Basak, S. and Chakraborty, C. (2015) Dual Stator Winding Induction Machine: Problems, Progress, and Future Scope. IEEE Transactions on Industrial Electronics, 62, 4641-4652.
http://dx.doi.org/10.1109/TIE.2015.2409800 - 13. Moradian, M. and Soltani, J. (2016) An Isolated Three-Phase Induction Generator System With Dual Stator Winding Sets Under Unbalanced Load Condition. IEEE Transactions on Energy Conversion, 99, 1-9.
http://dx.doi.org/10.1109/tec.2015.2508958 - 14. Khlifi, M.A. and Alshammari, B.M. (2014) Steady-State Analysis of an Isolated Self-Excited Dual Three-Phase Induction Generator for Renewable Energy. International Journal of Modern Nonlinear Theory and Application, 3, 191-198.
http://dx.doi.org/10.4236/ijmnta.2014.35021 - 15. Bu, F., Hu, Y., Huang, W., Zhuang, S. and Shi, K. (2014) Control Strategy and Dynamic Performance of Dual Stator-Winding Induction Generator Variable Frequency AC Generating System with Inductive and Capacitive Loads. IEEE Transactions on Power Electronics, 29, 1681-1692.
http://dx.doi.org/10.1109/TPEL.2013.2265099 - 16. Ojo, O. and Davidson, I.E. (1999) PWM-VSI Inverter Assisted Stand-Alone Dual Stator Winding Induction Generator. The IEEE Thirty-Fourth IAS Annual Meeting, Conference Record of the Industry Applications, Phoenix, 3-7 October 1999, 1573-1580.
http://dx.doi.org/10.1109/ias.1999.805950 - 17. Ojo, O. and Davidson, I.E. (2000) A Dual Stator Winding Induction Generator with a Four Switch Inverter-Battery Scheme for Control. The IEEE 31st Annual in Power Electronics Specialists Conference, Galway, 23 June 2000, 230-234.
http://dx.doi.org/10.1109/pesc.2000.878846 - 18. Zhang, B., Wang, D., Ma, W., Xiao, F. and Hu, A. (2005) The Excitation Control of a 12/3 Phase Dual Stator-Winding Induction Generator. The 31st Annual Conference of IEEE Industrial Electronics Society IECON, 6-10 November 2005, 6.
- 19. Dong, W., Weiming, M., Fei, X., Botao, Z., Dezhi, L. and An, H. (2005) A Novel Stand-Alone Dual Stator-Winding Induction Generator with Static Excitation Regulation. IEEE Transactions on Energy Conversion, 20, 826-835.
http://dx.doi.org/10.1109/TEC.2005.853744 - 20. Nielsen, J.G., Newman, M., Nielsen, H. and Blaabjerg, F. (2004) Control and Testing of a Dynamic Voltage Restorer (DVR) at a Medium Voltage Level. IEEE Transactions on Power Electronics, 19, 806-813.
http://dx.doi.org/10.1109/TPEL.2004.826504 - 21. Cartwright, P.A. (1952) A Passive Compensator for Voltage Flicker [Includes Discussion]. Electrical Engineering, 71, 1032-1035.
http://dx.doi.org/10.1109/ee.1952.6437794 - 22. Singh, B., Chandra, A. and Al-Haddad, K. (2014) Power Quality: Problems and Mitigation Techniques. John Wiley & Sons.
- 23. Singh, G.K., Yadav, K.B. and Saini, R.P. (2005) Modeling and Analysis of Multi-Phase (six-phase) Self-Excited Induction Generator. The IEEE Eighth International Conference on Electrical Machines and Systems (ICEMS), Nanjing, 29-29 September 2005, 1922-1927.
- 24. Amimeur, H., Abdessemed, R., Aouzellag, D., Merabet, E. and Hamoudi, F. (2008) Modeling and Analysis of Dual-Stator Windings Self-Excited Induction Generator. Journal of Electrical Engineering (JEE), 8, 3.


























