International Journal of Astronomy and Astrophysics
Vol.09 No.04(2019), Article ID:97273,18 pages
10.4236/ijaa.2019.94027
New Probability Distributions in Astrophysics: I. The Truncated Generalized Gamma
Lorenzo Zaninetti
Physics Department, Turin, Italy

Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 7, 2019; Accepted: December 20, 2019; Published: December 23, 2019
ABSTRACT
The gamma function is a good approximation to the luminosity function of astrophysical objects, and a truncated gamma distribution would permit a more rigorous analysis. This paper examines the generalized gamma distribution (GG) and then introduces the scale and the new double truncation. The magnitude version of the truncated GG distribution with scale is adopted in order to fit the luminosity function (LF) for galaxies or quasars. The new truncated GG LF is applied to the five bands of SDSS galaxies, to the 2dF QSO Redshift Survey in the range of redshifts between 0.3 and 0.5, and to the COSMOS QSOs in the range of redshifts between 3.7 and 4.7. The average absolute magnitude versus redshifts for SDSS galaxies and QSOs of 2dF was modeled adopting a redshift dependence for the lower and upper absolute magnitude of the new truncated GG LF.
Keywords:
Probability Distributions, Quasars, Galaxies

1. Introduction
The generalized gamma distribution (GG) was introduced by [1] and carefully analyzed by [2]. The GG has three-parameters and the techniques to find them is a matter of research, see among others [3] [4] [5]. A significant role in astrophysics is played by the luminosity function (LF) for galaxies and we present some models, among others, the Schechter LF, see [6], a two-component Schechter—like LF, see [7], and the double Schechter LF with five parameters, see [8]. Another approach starts from a given statistical distribution for which the probability density function (PDF) is known. We know that for a given PDF, ,
(1)
where L is the luminosity. A data oriented LF, , is obtained by adopting which is the normalization to the number of galaxies in a volume of 1 Mpc3
(2)
which means
(3)
The above line of research allows exploring the LF for galaxies in the framework of well studied PDFs. Some examples are represented by the mass-luminosity relationship, see [9], some models connected with the generalized gamma (GG) distribution, see [10] [11], the truncated beta LF, see [12], the lognormal LF, see [13], the truncated lognormal LF, see [14], and the Lindley LF, see [15].
This paper brings up the GG and introduces the scale in Section 2. The new double truncation for the GG and the GG with scale is introduced in Section 3. The derivation of the truncated GG LF is done in Section 4. Section 5 contains the application of the GG LF to galaxies and quasars as well the fit of the averaged absolute magnitude for QSOs as function of the redshift.
2. The Generalized Gamma Distribution
Let X be a random variable defined in ; the GG (PDF), , is
(4)
where
(5)
is the gamma function, with , and . The above PDF can be obtained by setting the location parameter equal to zero in the four parameters GG as given by [16], pag. 113. The GG PDF scale as and the gamma PDF as : the introduction of the parameter c increases the flexibility of the GG.
The GG family includes several subfamilies, including the exponential PDF when and , the gamma PDF when and the Weibull PDF when .
The distribution function (DF), , is
(6)
where is the incomplete Gamma function, defined by
(7)
see [17]. The average value or mean, , is
(8)
the variance, , is
(9)
The mode, M, is
(10)
The rth moment about the origin is, , is
(11)
The information entropy, H, is
(12)
where is the digamma or Psi function defined as
(13)
where , see [17].
The Scale
In some applications it may be useful to have a scale, b, and therefore the GG PDF, , is
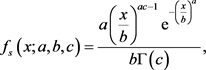 (14)
(14)
which has DF, 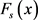 , as
, as
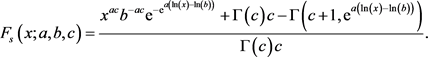 (15)
(15)
The average value,  , is
, is
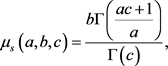 (16)
(16)
the variance, 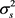 , is
, is
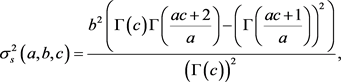 (17)
(17)
and the mode, 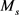 , is
, is
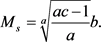 (18)
(18)
3. Double Truncation
Let X be a random variable defined in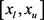 ; the new double truncated GG PDF,
; the new double truncated GG PDF, 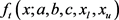 , can be found by evaluating of the following integral
, can be found by evaluating of the following integral
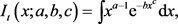 (19)
(19)
which is
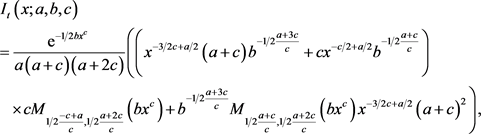 (20)
(20)
where 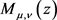 is the Whittaker M function, see Appendix A. We now define the constant of integration,
is the Whittaker M function, see Appendix A. We now define the constant of integration, 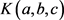 , as
, as
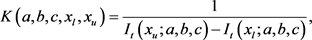 (21)
(21)
and as a consequence the truncated GG PDF is, 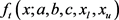 ,
,
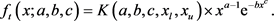 (22)
(22)
The average value, 

where




The DF, 

where



The Scale
The truncated GG PDF with scale requires the evaluation of the following integral, 

which is

The constant of integration, 

and as a consequence the truncated GG PDF with scale is, 

The average value, 

where




4. The Luminosity Function
In this section we present the Schechter LF, we derive the GG LF, we introduce the double truncation in the LF and we develop the adopted statistics.
4.1. The Schechter LF
The Schechter LF, introduced by [6], is

here 



The equivalent distribution in absolute magnitude is

where 




4.2. Generalized Gamma LF
We replace in the GG with scale, see Equation (14) x with L (the luminosity), b with 


The magnitude version is

where M is the absolute magnitude and 
4.3. Double Truncation for the LF
We replace in the truncated GG with scale, see Equation (35), x with L (the luminosity), b with 






where 


The four luminosities 





where the indexes u and l are inverted in the transformation from luminosity to absolute magnitude and 

The magnitude version of the truncated GG LF is



The averaged absolute magnitude is

4.4. The Adopted Statistics
The unknown parameters of the LF can be found through the Levenberg-Marquardt method (subroutine MRQMIN in [18] ) but the first derivative of the LF with respect to the unknown parameters should be provided. In the case of the truncated GG LF, see Equation (49), the first derivative with respect to the unknown parameters has a complicated expression, so we used the numerical first derivative. The merit function 

where n is number of datapoints and the two indexes theo and astr stand for theoretical and astronomical, respectively. The residual sum of squares (RSS) is

where 



where

where L is the likelihood function and k the number of free parameters in the model. We assume a Gaussian distribution for the errors and the likelihood
function can be derived by the 



The Bayesian information criterion (BIC), see [22], is

where L is the likelihood function, k the number of free parameters in the model and n the number of observations. The phrase “better fit” used in the following means that the three statistical indicators:
5. Astrophysical Applications
In this section we apply the truncated GG LF to the SDSS galaxies and to QSOs. The introduction of the redshift dependence for lower and upper absolute magnitude allows to model the average absolute magnitude versus redshift for QSOs.
5.1. SDSS Galaxies
In order to perform a test we selected the data of the Sloan Digital Sky Survey (SDSS) which has five bands 












Table 1. Parameters for fits to LF in SDSS Galaxies with the four parameters truncated GG LF as represented by formula (49).
The Schechter function, the new four parameters function as represented by formula (49) and the data are reported in Figures 1-5, where bands




Table 2 presents the luminosity density evaluated with the Schechter LF, j, and with the truncated GG LF, jT. The range of existence in the truncated case is finite rather than infinite and therefore the luminosity density is always smaller than in the standard case.
5.2. Luminosity Function for QSOs
For our first example, we selected the catalog of the 2dF QSO Redshift Survey (2QZ), which contains 22431 redshifts of QSOs with

In the second example we explored the faint LF for quasars in the range of redshifts 
5.3. Average Absolute Magnitude versus Redshift
The first application is about galaxies: we processed the SDSS Photometric Catalogue DR 12, see [28], which contains 10,450,256 galaxies (elliptical + spiral) with redshift and rest frame 

Figure 1. The luminosity function data of SDSS(u*) are represented with error bars. The continuous line fit represents the four parameters truncated GG LF (49) and the dotted line represents the Schechter function.
Figure 2. The luminosity function data of SDSS(g*) are represented with error bars. The continuous line fit represents the four parameters truncated GG LF (49) and the dotted line represents the Schechter function.
Table 2. Luminosity density in SDSS Galaxies evaluated with the Schechter LF, formula (42), and with the four parameters truncated GG LF, formula (47), when 

Figure 3. The luminosity function data of SDSS(r*) are represented with error bars. The continuous line fit represents the four parameters truncated GG LF (49) and the dotted line represents the Schechter function.
Figure 4. The luminosity function data of SDSS(i*) are represented with error bars. The continuous line fit represents the four parameters truncated GG LF (49) and the dotted line represents the Schechter function.
Table 3. The four parameters truncated GG LF as represented by formula (49) in the QSO case.
Table 4. The four parameters truncated GG LF as represented by formula (49) for QSOs in the COSMOS field.
Figure 5. The luminosity function data of SDSS(z*) are represented with error bars. The continuous line fit represents the four parameters truncated GG LF (49) and the dotted line represents the Schechter function.
Figure 6. The observed LF for QSOs, empty stars with error bar, when z [0.3, 0.5] and M [−24.93, −22.29]. The continuous line fit represents the four parameters truncated GG LF (49).
Figure 7. The observed LF for QSOs in the COSMOS field, empty stars with error bar, when z [3.7, 4.7] and M [−28, −22]. The continuous line fit represents the four parameters truncated GG LF (49).
The second application is about the QSO and we used the framework of the flat cosmology in order to find the absolute magnitude relative to the catalog of the 2dF QSO Redshift Survey (2QZ), exactly as [26]. The two cosmological parameters are 




Figure 8. Average observed absolute magnitude versus redshift for SDSS galaxies (red points), average theoretical absolute magnitude for the four parameters of the truncated GG LF as given by Equation (52) (dot-dash-dot green line), the lowest absolute magnitude is 



where G is the Newtonian gravitational constant and 


The above equation represents a useful theoretical reference. Another, more empirical, way explores numerically the maximum and the minimum in absolute magnitude functions of the redshift for the sample 2QZ. In order to fix the numbers we fitted the upper absolute magnitude with the third degree polynomial

with




with


Figure 9. Average observed absolute magnitude versus redshift for QSOs (red points), average theoretical absolute magnitude for the four parameters of the truncated GG LF as given by Equation (52) (dot-dash-dot green line), the lowest absolute magnitude at a given redshift as given by the sample (full black line) and the highest absolute magnitude at a given redshift as given by the sample (dashed black line); RSS = 1.62.

Now different combinations of curves can be used. Figure 9 presents the combination which minimizes the RSS.
6. Conclusions
Truncated GG: We derived an expression for the left and right truncated GG PDF in terms of the Whittaker M function, see Equation (22), its DF, see Equation (28), and its average value, see Equation (23).
Truncated LF: The truncated LF for galaxies or QSO is derived both in the luminosity form, see Equation (46), and in the magnitude form, see Equation (49). In all the astrophysical examples here analyzed which are the five bands of SDSS galaxies, see Table 1, the QSOs when


Average Magnitude versus redshift: The averaged absolute magnitude of the SDSS galaxies and QSOs belonging to the catalog 2QZ as functions of the redshift are reasonably fitted by the averaged absolute magnitude of the truncated GG LF, see Equation (52). In order to perform the fit we provided for 
Conflicts of Interest
The author declares no conflicts of interest regarding the publication of this paper.
Cite this paper
Zaninetti, L. (2019) New Probability Distributions in Astrophysics: I. The Truncated Generalized Gamma. International Journal of Astronomy and Astrophysics, 9, 393-410. https://doi.org/10.4236/ijaa.2019.94027
References
- 1. Stacy, E.W., et al. (1962) A Generalization of the Gamma Distribution. The Annals of Mathematical Statistics, 33, 1187-1192. https://doi.org/10.1214/aoms/1177704481
- 2. Khodabina, M. and Ahmadabadib, A. (2010) Some Properties of Generalized Gamma Distribution. Mathematical Sciences, 4, 9-28.
- 3. Stacy, E.W. and Mihram, G.A. (1965) Parameter Estimation for a Generalized Gamma Distribution. Technometrics, 7, 349-358. https://doi.org/10.2307/1266594
- 4. Gomès, O., Combes, C. and Dussauchoy, A. (2008) Parameter Estimation of the Generalized Gamma Distribution. Mathematics and Computers in Simulation, 79, 955-963. https://doi.org/10.1016/j.matcom.2008.02.006
- 5. Lakshmi, R.V. and Vaidyanathan, V.S. (2016) Three-Parameter Gamma Distribution: Estimation Using Likelihood, Spacings and Least Squares Approach. Journal of Statistics and Management Systems, 19, 37-53. https://doi.org/10.1080/09720510.2014.986927
- 6. Schechter, P. (1976) An Analytic Expression for the Luminosity Function for Galaxies. The Astrophysical Journal, 203, 297-306. https://doi.org/10.1086/154079
- 7. Driver, S.P. and Phillipps, S. (1996) Is the Luminosity Distribution of Field Galaxies Really Flat? The Astrophysical Journal, 469, 529-534. https://doi.org/10.1086/177801
- 8. Blanton, M.R., Lupton, R.H., Schlegel, D.J., Strauss, M.A., Brinkmann, J., Fukugita, M. and Loveday, J. (2005) The Properties and Luminosity Function of Extremely Low Luminosity Galaxies. The Astrophysical Journal, 631, 208-230. https://doi.org/10.1086/431416
- 9. Zaninetti, L. (2008) A New Luminosity Function for Galaxies as Given by the Mass-Luminosity Relationship. The Astronomical Journal, 135, 1264-1275. https://doi.org/10.1088/0004-6256/135/4/1264
- 10. Zaninetti, L. (2010) The Luminosity Function of Galaxies as Modelled by the Generalized Gamma Distribution. Acta Physica Polonica B, 41, 729-751.
- 11. Zaninetti, L. (2014) A Near Infrared Test for Two Recent Luminosity Functions for Galaxies. Revista Mexicana de Astronomia y Astrofisica, 50, 7-14.
- 12. Zaninetti, L. (2014) The Luminosity Function of Galaxies as Modeled by a Left Truncated Beta Distribution. International Journal of Astronomy and Astrophysics, 4, 145-154. https://doi.org/10.4236/ijaa.2014.41013
- 13. Zaninetti, L. (2018) A Lognormal Luminosity Function for Swire in Flat Cosmology. Advances in Astrophysics, 3, 239-249. https://doi.org/10.22606/adap.2018.34003
- 14. Zaninetti, L. (2016) The Truncated Lognormal Distribution as a Luminosity Function for SWIFT-BAT Gamma-Ray Bursts. Galaxies, 4, 57-74. https://doi.org/10.3390/galaxies4040057
- 15. Zaninetti, L. (2019) The Truncated Lindley Distribution with Applications in Astrophysics. Galaxies, 7, 61. https://doi.org/10.3390/galaxies7020061
- 16. Forbes, C., Evans, M., Hastings, N. and Peacock, B. (2011) Statistical Distributions. Fourth Edition, John Wiley & Sons, Hoboken. https://doi.org/10.1002/9780470627242
- 17. Olver, F.W.J., Lozier, D.W., Boisvert, R.F. and Clark, C.W. (2010) NIST Handbook of Mathematical Functions. Cambridge University Press, Cambridge.
- 18. Press, W.H., Teukolsky, S.A., Vetterling, W.T. and Flannery, B.P. (1992) Numerical Recipes in FORTRAN. The Art of Scientific Computing. Cambridge University Press, Cambridge.
- 19. Akaike, H. (1974) A New Look at the Statistical Model Identification. IEEE Transactions on Automatic Control, 19, 716-723. https://doi.org/10.1109/TAC.1974.1100705
- 20. Liddle, A.R. (2004) How Many Cosmological Parameters? Monthly Notices of the Royal Astronomical Society, 351, L49-L53. https://doi.org/10.1111/j.1365-2966.2004.08033.x
- 21. Godlowski, W. and Szydowski, M. (2005) Constraints on Dark Energy Models from Supernovae. In: Turatto, M., Benetti, S., Zampieri, L. and Shea, W., Eds., 1604-2004: Supernovae as Cosmological Lighthouses, Astronomical Society of the Pacific, Vol. 342 of Astronomical Society of the Pacific Conference Series, 508-516.
- 22. Schwarz, G. (1978) Estimating the Dimension of a Model. Annals of Statistics, 6, 461-464. https://doi.org/10.1214/aos/1176344136
- 23. Gunn, J.E., Carr, M., Rockosi, C., Sekiguchi, M., Berry, K., Elms, B., de Haas, E., Ivezić, Z., Knapp, G., Lupton, R. and Pauls, G. (1998) The Sloan Digital Sky Survey Photometric Camera. The Astronomical Journal, 116, 3040-3081. https://doi.org/10.1086/300645
- 24. Blanton, M.R., Hogg, D.W., Bahcall, N.A., Brinkmann, J. and Britton, M. (2003) The Galaxy Luminosity Function and Luminosity Density at Redshift z = 0.1. The Astrophysical Journal, 592, 819-838. https://doi.org/10.1086/375776
- 25. Croom, S.M., Smith, R.J., Boyle, B.J., Shanks, T., Miller, L., Outram, P.J. and Loaring, N.S. (2004) The 2dF QSO Redshift Survey XII. The Spectroscopic Catalogue and Luminosity Function. Monthly Notices of the Royal Astronomical Society, 349, 1397-1418. https://doi.org/10.1111/j.1365-2966.2004.07619.x
- 26. Zaninetti, L. (2017) A Left and Right Truncated Schechter Luminosity Function for Quasars. Galaxies, 5, 25-40. https://doi.org/10.3390/galaxies5020025
- 27. Ikeda, H., Nagao, T., Matsuoka, K., Taniguchi, Y., et al. (2011) Probing the Faint End of the Quasar Luminosity Function at z 4 in the COSMOS Field. The Astrophysical Journal Letters, 728, L25. https://doi.org/10.1088/2041-8205/728/2/L25
- 28. Alam, S., Albareti, F.D., Allende Prieto, C., et al. (2015) The Eleventh and Twelfth Data Releases of the Sloan Digital Sky Survey: Final Data from SDSS-III. The Astrophysical Journal, 219, 12.
- 29. Abramowitz, M. and Stegun, I.A. (1965) Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Dover, New York.
Appendix A: The Whittaker M function
The Whittaker M function, 

The regularized hypergeometric function, 

where


The generalized hypergeometric series is denoted by 



The relationship

allows to express the Whittaker M function in terms of the generalized hypergeometric function, 











