Engineering, 2013, 5, 221-225
doi:10.4236/eng.2013.51b040 Published Online January 2013 (http://www.SciRP.org/journal/eng)
Randomized Integral Gain of Pi Current Controller for
A Single Pv Inverter System
Suriana Salimin1*, Matthew Armstrong2, Bashar Zahawi2
1University Tun Hussein Onn Malaysia, Fakulty of Electric and Electronic, Parit Raja, Batu Pahat, Malaysia
2Newcastle University, School of Electrical, Electronic and Computer, Engineering, Newcastle Upon Tyne, UK
Received 2013
ABSTRACT
This paper is concerned with the problem of network power quality when grid connected systems are used to feed the
grid. These systems use power electronic components such as inverters that produce harmonics which adversely affect
the power quality of the distribution network. Instead of using a conventional PI current controller with a fixed propor-
tional and integral gain, development of new control method is considered to overcome the total harmonic emissions in
PV inverters. It considers a modification to the controller where a random integral gain is used in the system. Experi-
mental hardware is developed and result shows a reduced total harmonic distortion (THD) of the output current when
tested with a resistive load.
Keywords: Total Harmonic Distortion; Single Inverter; Current Controller
1. Introduction
In recent years, as technology has improved, distributed
generators from solar have become more popular and
have been increasingly used as an alternative to coal, gas
and oil. Besides its cleanest energy source, solar is also
well known as the renewable energy that can always be
relied on to continuously supplying electricity and meets
users demand.
Figure 1 illustrates the basic concept of single PV grid
connected inverter. It typically consists of a PV array,
DC-DC boost converter, DC-AC inverter, a filter, and the
grid. A 50Hz isolation transformer is normally used be-
tween the filter and the grid to ensure galvanic isolation
between the grid and the PV system as well as to guar-
antee zero DC current injection into the network.
Much research on PV system has been done to inves-
tigate its efficiency. Often, grid connected inverters pro-
duce harmonics which can exceed power quality standards.
The various types of harmonics are often being catego-
rised as switching harmonics [1], low order harmonics
[1], and DC current injection [2]. A.Testa et.al [3] also
demonstrated that inter-harmonics and sub-harmonics are
an additional source of harmonic pollution which may
need to be considered. Switching harmonics are the high
order harmonics generally in kHz range generated due to
the high frequency of inverter switching whilst the defi-
ciencies in the inverter current controller are being the
cause of low order harmonics generation typically at in-
teger multiples closer to fundamental frequency. The
causes of DC current injections have been observed sim-
ply from the imperfect inverters that do not completely
invert all DC components to AC. Inter-harmonics at the
other hand occur at the frequencies that are not fixed at
integral multiples of fundamental. Their frequencies are
variable and difficult to trace. These inter-harmonic
components may cause sub-synchronous oscillations,
voltage fluctuations and light flicker. V.E.Wagner et.al [4]
has summarised the effects of harmonics on many
equipments including circuit breakers, transformers, me-
tering and lighting. In the paper, they highlighted two
groups of harmonic effects; the heating effects and the
disturbance in equipments operation. Subjak and Mcquilkin
[5] have also analysed the causes, effects and measure-
ments of harmonics. The paper briefly explained the
definition of harmonics and how harmonics can cause
communication interference, heating, as well as solid-
state device malfunction.
On the other hand, a paper by H.Soo et.al [6] stated a
different view about low order harmonics. It demon-
strated that low order harmonics profile can actually be
Figure 1. Basic concept of grid connected inverter.

S. SALIMIN ET AL.
222
affected when the condition of grid voltage varies due to
the changes in the grid impedance and the connection of
non-linear loads. Although it suggested an adaptive con-
trol algorithm in order to compensate the problems, the
result is still uncertain.
To improve the harmonic performance of grid con-
nected inverter systems, it is possible to make improve-
ments to the power electronic converter hardware; in-
verter topology [7,8], PWM switching schemes [9-11],
and so on. Alternatively, it is possible to enhance the
performance and robustness of the current controller [1,
12-14]. This paper focuses on control methods for im-
proving the low order harmonic performance of PV in-
verter systems. Literature research has shown that a
number of unique control schemes have been presented,
all with their associated merits and disadvantages. In this
paper, a modification is made to the integral gain of the
conventional PI current controller to produce a new con-
trol scheme capable of minimising the low order har-
monics in the grid connected inverter systems.
The aims of this paper are:
● To demonstrate the poor low order harmonic per-
formance of grid connected inverters using conven-
tional PI control methods.
● To demonstrate that Control Parameter Randomi-
sation of one of the PI gain can further improve the
harmonic performance of grid connected inverters.
2. System Description
Two main parts of systems must be identify and under-
stand first; the PWM technique and the inverter current
control technique. PWM is used as a switching technique
to drive the gate signals of the inverter. Whereas, the
current control technique is used to response and com-
pensate the inverter current.
2.1. PWM Switching
In this project, a unipolar PWM technique as in Figure 2
is used as the switching technique for the H-bridge in-
verter. Each output from the switching scheme is fed to
each of the switching devices of the inverter. It works as
explained below:
If
Vsine > Vcarrier ; Out 1 will turn on Switch 1
Vsine < Vcarrier ; Out 2 will turn on Switch 2
-Vsine > Vcarrier ; Out 3 will turn on Switch 3
-Vsine < Vcarrier ; Out 4 will turn on Switch 4
Figure 3 illustrates the H-bridge inverter with Switch
1 to Switch 4 as mentioned above.
2.2. Current Controller
In this project, rather than the proportional, integral and
derivative (PID) system, only the proportional (P) and
integral (I) terms are used in the current controller system.
This type of controller is the most common controller
applied as the inverter current feedback process. The
term P will give an output that is proportional to the sys-
tem error which is the difference between the system
output value and the desired value. It has a gain, Kp
which will multiply the error and response to it. The
purpose is to reduce the rise time of the system. However,
using this proportional term alone will result in having a
system stationary error. In order to eliminate this error
and complete the P based control, the integral part is used.
The output of the integral part is the multiplication of a
gain, Ki and the summing of the previous errors to the
current system error. This is a continuous process which
will stop if the system signal or the system output value
matches the desired value demanded by the user.
The analogue PI transfer function is

I
PI P
K
Gs K
s
 (1)
After the conversion to the discrete domain by the
method of z-transform analysis, the transfer function
becomes
Figure 2. A unipolar PWM switching.
Figure 3. H-bridge inverter system.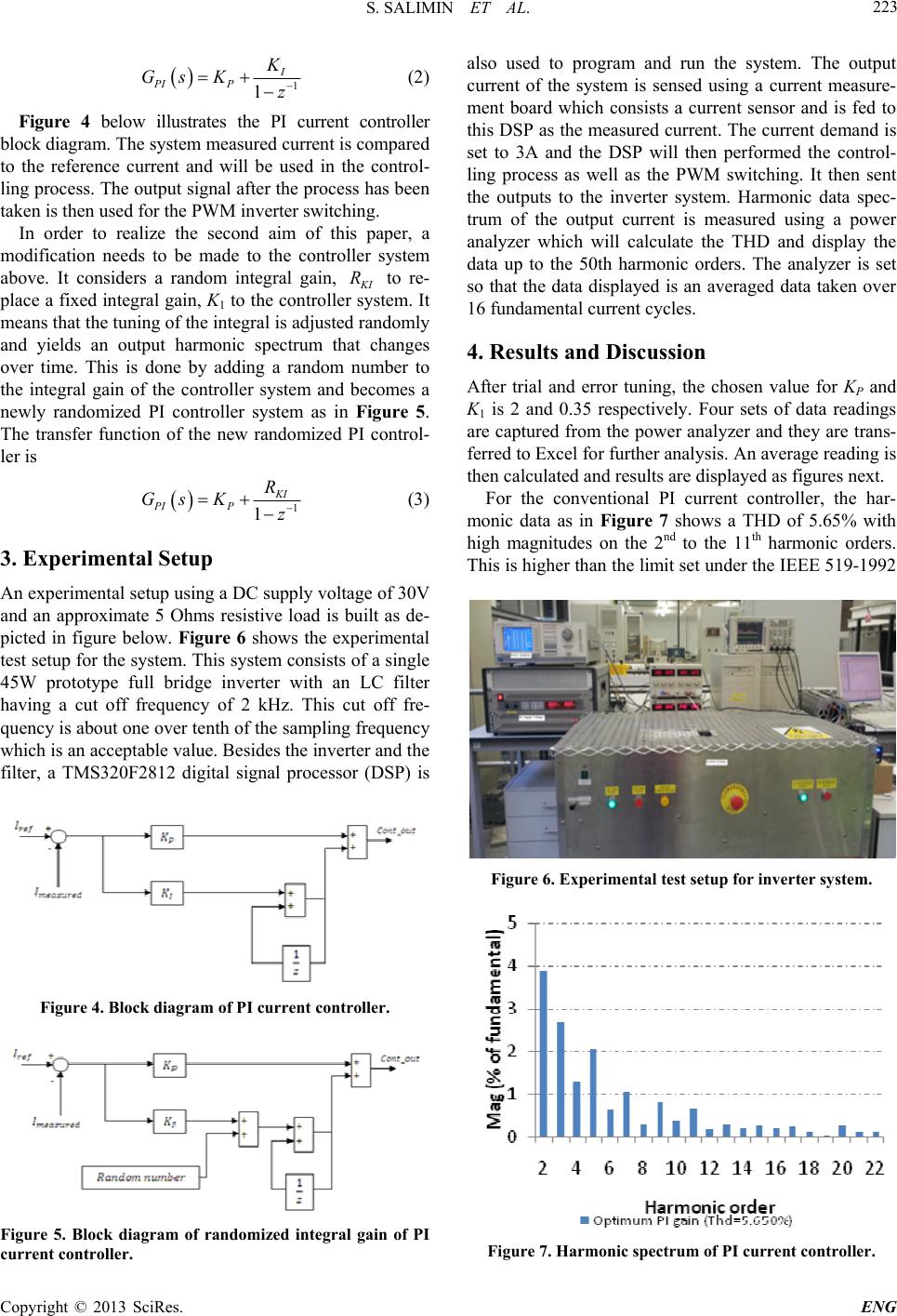

S. SALIMIN ET AL.
223

1
1
I
PI P
K
Gs Kz 
 (2)
Figure 4 below illustrates the PI current controller
block diagram. The system measured current is compared
to the reference current and will be used in the control-
ling process. The output signal after the process has been
taken is then used for the PWM inverter switching.
In order to realize the second aim of this paper, a
modification needs to be made to the controller system
above. It considers a random integral gain,
K
I
R to re-
place a fixed integral gain, K1 to the controller system. It
means that the tuning of the integral is adjusted randomly
and yields an output harmonic spectrum that changes
over time. This is done by adding a random number to
the integral gain of the controller system and becomes a
newly randomized PI controller system as in Figure 5.
The transfer function of the new randomized PI control-
ler is

1
1
KI
PIP R
Gs Kz 
 (3)
3. Experimental Setup
An experimental setup using a DC supply voltage of 30V
and an approximate 5 Ohms resistive load is built as de-
picted in figure below. Figure 6 shows the experimental
test setup for the system. This system consists of a single
45W prototype full bridge inverter with an LC filter
having a cut off frequency of 2 kHz. This cut off fre-
quency is about one over tenth of the sampling frequency
which is an acceptable value. Besides the inverter and the
filter, a TMS320F2812 digital signal processor (DSP) is
Figure 4. Block diagram of PI current controller.
Figure 5. Block diagram of randomized integral gain of PI
current con t r o ller.
also used to program and run the system. The output
current of the system is sensed using a current measure-
ment board which consists a current sensor and is fed to
this DSP as the measured current. The current demand is
set to 3A and the DSP will then performed the control-
ling process as well as the PWM switching. It then sent
the outputs to the inverter system. Harmonic data spec-
trum of the output current is measured using a power
analyzer which will calculate the THD and display the
data up to the 50th harmonic orders. The analyzer is set
so that the data displayed is an averaged data taken over
16 fundamental current cycles.
4. Results and Discussion
After trial and error tuning, the chosen value for KP and
K1 is 2 and 0.35 respectively. Four sets of data readings
are captured from the power analyzer and they are trans-
ferred to Excel for further analysis. An average reading is
then calculated and results are displayed as figures next.
For the conventional PI current controller, the har-
monic data as in Figure 7 shows a THD of 5.65% with
high magnitudes on the 2nd to the 11th harmonic orders.
This is higher than the limit set under the IEEE 519-1992
Figure 6. Experimental test setup for inverter system.
Figure 7. Harmonic spectrum of PI current controller.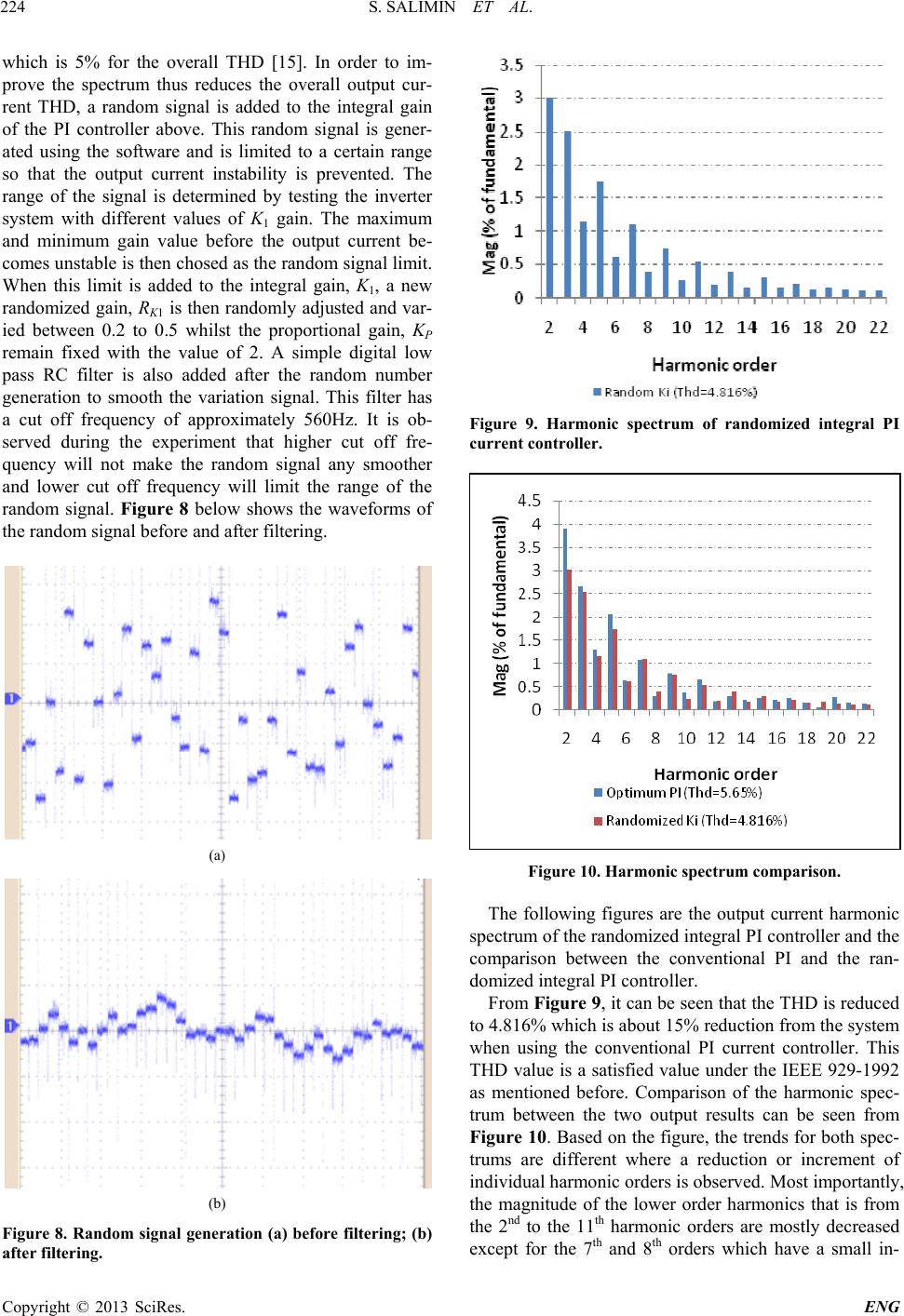

S. SALIMIN ET AL.
224
which is 5% for the overall THD [15]. In order to im-
prove the spectrum thus reduces the overall output cur-
rent THD, a random signal is added to the integral gain
of the PI controller above. This random signal is gener-
ated using the software and is limited to a certain range
so that the output current instability is prevented. The
range of the signal is determined by testing the inverter
system with different values of K1 gain. The maximum
and minimum gain value before the output current be-
comes unstable is then chosed as the random signal limit.
When this limit is added to the integral gain, K1, a new
randomized gain, RK1 is then randomly adjusted and var-
ied between 0.2 to 0.5 whilst the proportional gain, KP
remain fixed with the value of 2. A simple digital low
pass RC filter is also added after the random number
generation to smooth the variation signal. This filter has
a cut off frequency of approximately 560Hz. It is ob-
served during the experiment that higher cut off fre-
quency will not make the random signal any smoother
and lower cut off frequency will limit the range of the
random signal. Figure 8 below shows the waveforms of
the random signal before and after filtering.
(a)
(b)
Figure 8. Random signal generation (a) before filtering; (b)
after filteri ng.
Figure 9. Harmonic spectrum of randomized integral PI
current con t r o ller.
Figure 10. Harmonic spectrum comparison.
The following figures are the output current harmonic
spectrum of the randomized integral PI controller and the
comparison between the conventional PI and the ran-
domized integral PI controller.
From Figure 9, it can be seen that the THD is reduced
to 4.816% which is about 15% reduction from the system
when using the conventional PI current controller. This
THD value is a satisfied value under the IEEE 929-1992
as mentioned before. Comparison of the harmonic spec-
trum between the two output results can be seen from
Figure 10. Based on the figure, the trends for both spec-
trums are different where a reduction or increment of
individual harmonic orders is observed. Most importantly,
the magnitude of the lower order harmonics that is from
the 2nd to the 11th harmonic orders are mostly decreased
except for the 7th and 8th orders which have a small in-

S. SALIMIN ET AL.
225
crement. Harmonic orders beyond the 11th show a fair
reduction as well as increment. This behaviour of having
a reduction and increment in harmonic orders magnitude
yields to the reduction of the Total Harmonic Distortion
(THD) of inverter system when using the proposed
method.
5. Conclusions
This paper has proposed a modified PI current controller
to overcome the issue of higher THD in a single inverter
system when using the conventional PI current controller.
This modification includes the integral gain, K1 of the PI
controller to be adjusted automatically using the ran-
domized integral gain, RK1 whilst the proportional gain,
KP of the controller remain the same. Experimental re-
sults show an improved THD performance by 15% com-
pared to the system when using the conventional PI
method. With no further components are required in or-
der to implement the proposed method, the total cost of
the PV inverter system remains unchanged.
6. Acknowledgements
This project is part of the principle author`s research
project to complete her PhD study in Newcastle Univer-
sity, UK. She would like to show her gratitude to Uni-
versity Tun Hussein Onn Malaysia for the sponsorship
during the study.
REFERENCES
[1] M. Armstrong, D. J. Atkinson, C. M. Johnson, and T. D.
Abeyasekera, "Low order harmonic cancellation in a grid
connected multiple inverter system via current control
parameter randomization," IEEE Transactions on Power
Electronics, vol. 20, pp. 885-892, 2005.
[2] M. Armstrong, D. J. Atkinson, C. M. Johnson, and T. D.
Abeyasekera, "Auto-calibrating dc link current sensing
technique for transformerless, grid connected, H-bridge
inverter systems," IEEE Transactions on Power Elec-
tronics, vol. 21, pp. 1385-1393, 2006.
[3] A. Testa, M. F. Akram, R. Burch, G. Carpinelli, G. Chang,
V. Dinavahi, C. Hatziadoniu, W. M. Grady, E. Gunther,
M. Halpin, P. Lehn, Y. Liu, R. Langella, M. Lowenstein,
A. Medina, T. Ortmeyer, S. Ranade, P. Ribeiro, N. Wat-
son, J. Wikston, and W. Xu, "Interharmonics: Theory and
Modeling," Power Delivery, IEEE Transactions on, vol.
22, pp. 2335-2348, 2007.
[4] V. E. Wagner, J. C. Balda, D. C. Griffith, A. McEachern,
T. M. Barnes, D. P. Hartmann, D. J. Phileggi, A. E.
Emannuel, W. F. Horton, W. E. Reid, R. J. Ferraro, and
W. T. Jewell, "Effects of harmonics on equipment,"
Power Delivery, IEEE Transactions on, vol. 8, pp.
672-680, 1993.
[5] J. S. Subjak, Jr. and J. S. McQuilkin, "Harmonics-causes,
effects, measurements, and analysis: an update," Industry
Applications, IEEE Transactions on, vol. 26, pp.
1034-1042, 1990.
[6] G. Hong Soo, M. Armstrong, and B. Zahawi, "The effect
of grid operating conditions on the current controller per-
formance of grid connected photovoltaic inverters," in
Power Electronics and Applications, 2009. EPE '09. 13th
European Conference on, 2009, pp. 1-8.
[7] J. Selvaraj and N. A. Rahim, "Multilevel Inverter For
Grid-Connected PV System Employing Digital PI Con-
troller," Industrial Electronics, IEEE Transactions on, vol.
56, pp. 149-158, 2009.
[8] M. Katiamoorthy, R. M. Sekar, and G. C. Raj, "A new
single-phase PV fed five-level inverter topology con-
nected to the grid," in Communication Control and Com-
puting Technologies (ICCCCT), 2010 IEEE International
Conference on, 2010, pp. 196-203.
[9] R. A. Villarreal-Ortiz, M. Hernandez-Angeles, C. R.
Fuerte-Esquivel, and R. O. Villanueva-Chavez, "Centroid
PWM technique for inverter harmonics elimination,"
Power Delivery, IEEE Transactions on, vol. 20, pp.
1209-1210, 2005.
[10] L. G. Franquelo, J. Napoles, R. C. P. Guisado, J. I. Leon,
and M. A. Aguirre, "A Flexible Selective Harmonic
Mitigation Technique to Meet Grid Codes in Three-Level
PWM Converters," Industrial Electronics, IEEE Transac-
tions on, vol. 54, pp. 3022-3029, 2007.
[11] M. A. A. Younis, N. A. Rahim, and S. Mekhilef, "High
efficiency THIPWM three-phase inverter for grid con-
nected system," in Industrial Electronics & Applications
(ISIEA), 2010 IEEE Symposium on, 2010, pp. 88-93.
[12] H. Qunhai, K. Li, W. Tongzhen, Z. Guowei, and K.
Lingzhi, "A new method for the photovoltaic
grid-connected inverter control," in Electric Utility De-
regulation and Restructuring and Power Technologies,
2008. DRPT 2008. Third International Conference on,
2008, pp. 2626-2629.
[13] M. Castilla, J. Miret, J. Matas, L. G. de Vicua, and J. M.
Guerrero, "Linear Current Control Scheme With Series
Resonant Harmonic Compensator for Single-Phase
Grid-Connected Photovoltaic Inverters," Industrial Elec-
tronics, IEEE Transactions on, vol. 55, pp. 2724-2733,
2008.
[14] R. Teodorescu, F. Blaabjerg, U. Borup, and M. Liserre,
"A new control structure for grid-connected LCL PV in-
verters with zero steady-state error and selective har-
monic compensation," in Applied Power Electronics
Conference and Exposition, 2004. APEC '04. Nineteenth
Annual IEEE, 2004, pp. 580-586 Vol.1.
[15] "IEEE Recommended Practices and Requirements for
Harmonic Control in Electrical Power Systems," IEEE
Std 519-1992, p. 0_1, 1993.