Applied Mathematics
Vol. 3 No. 7 (2012) , Article ID: 19873 , 14 pages DOI:10.4236/am.2012.37102
A Thermal Shock-Chemical Reactive Problem in Flow of Viscoelastic Fluid with Thermal Relaxation
1Department of Mathematics, Faculty of Sciences and Letters in Al Bukayriyyah, Al-Qassim University, Al-Qassim, KSA
2Department of Mathematics, Faculty of Education, Damanhuur University, Damanhuur, Egypt
Email: *maezzat2000@yahoo.com
Received April 20, 2012; revised May 20, 2012; accepted May 27, 2012
Keywords: MHD; Heat and Mass Transfer; Boundary Layer Theory; Viscoelastic Fluid; State Space Approach; Lord-Shulman Theory; Numerical Results
ABSTRACT
Effects of thermal and species diffusion with one relaxation time on the boundary layer flow of a viscoelastic fluid bounded by a vertical surface in the presence of transverse magnetic field have been studied. The state space approach developed by Ezzat [1] is adopted for the solution of one-dimensional problem for any set of boundary conditions. The resulting formulation together with the Laplace transform techniques are applied to a thermal shock-chemical reactive problem. The inversion of the Laplace transforms is carried out using a numerical approach. The numerical results of dimensionless temperature, concentration, velocity, and induced magnetic and electric fields distributions are given and illustrated graphically for the problem.
1. Introduction
Viscoelastic flows are encountered in numerous areas of petrochemical, biomedical and environmental engineering including polypropylene coalescence sintering [2] and geological flows [3]. A wide range of mathematical models have been developed to simulate the nonlinear stress-strain characteristics of such fluids which exhibit both viscous and elastic properties [4].
In nature and many industrial applications, there are plenty of transport processes where simultaneous heat and mass transfer is a common phenomenon. Its application is found in many diverse fields but not limited to cleaning operations, curing of plastics, manufacturing of pulp-insulated cables, many chemical processes such as analysis of polymers in chemical engineering, condensation and frosting of heat exchangers [5]. The study of convection reduces to the determination of convective heat and mass transfer coefficients. Convective heat and mass transfer coefficients are important parameters, which are a measure of the resistance to heat and mass transfer between a surface and the fluid flowing over that surface. The convective coefficients depend on the hydrodynamic, thermal and concentration boundary layers. In many of the internal flows, both forced and natural convection play major roles in the heat and mass transfer processes. Whereas in the entrance section of a duct, forced convection becomes dominant, as the flow moves towards the downstream section, natural convection could dominate over forced convection and finally in the thermally developed region natural convection becomes negligible. Natural convection may be due to a temperature or concentration gradient or both. If the buoyancy forces are due to temperature and concentration gradients that act in the same direction, both the heat and mass transfer will increase. However, if the temperature and concentration gradients act in the opposite direction, both heat and mass transfer reduce [6].
In recent years, the study of viscoelastic fluid flow is an important type of flow occurring in several engineering processes. Such processes are wire drawing, glass fiber and paper production, crystal growing, drawing of plastic sheets, among which we also cite many applications in petroleum in drilling, manufacturing of foods and slurry transporting. The boundary layer concept of such fluids is of special importance due to its applications to many engineering problems among which we cite the possibility of reducing frictional drag on the hulls of ships and submarines.
A great deal of works has been carried out on various aspects of momentum and heat transfer characteristics in a viscoelastic boundary layer fluid flow over a stretching plastic boundary [7] since the pioneering work of Sakiadis [8]. Ezzat and Zakaria [9] studied the effects of free convection currents with one relaxation time on the flow of a viscoelastic fluid through a porous medium. Khan and Sanjayanand [10] studied heat and mass transfer in a viscoelastic boundary layer flow over exponentially stretching sheet.
In this work, we use a more general model of MHD mixed convection flow of conducting viscoelastic fluid which also includes both the relaxation time in the heat and concentration equation and the electric permeability of the electromagnetic field. The unsteady free convection heat and mass transfer flow of electrically conducting incompressible viscoelastic fluid past an infinite vertical plate in the presence of a transverse magnetic field and chemical reaction using the state space approach and Laplace transforms technique. The inversion of the Laplace transform is carried out using a numerical technique [11].
2. Formulation of the Problem
The electro-magnetic quantities satisfy Maxwell’s equations [12]:
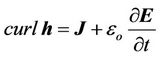 (1)
(1)
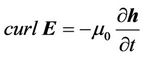 (2)
(2)
 ,
,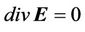 (3)
(3)
 ,
, (4)
(4)
These equations are supplemented by Ohm’s law
 (5)
(5)
Consider an unsteady free convection flow of electrically conducting incompressible, viscoelastic fluid past an infinite vertical plate. The x-axis is taken in the vertical direction along the plate and y-axis normal to it. Let u be the component of the velocity of the fluid in the x direction and a constant magnetic field acts in the y direction of strength . This produces an induced magnetic field
. This produces an induced magnetic field  and an induced electric field
and an induced electric field  as well as a conduction current density
as well as a conduction current density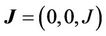 . All the considered functions will depend on y and the time t only.
. All the considered functions will depend on y and the time t only.
Equation (5) reduces to
 . (6)
. (6)
The vector Equations (1) and (2) reduced to the following scalar equation
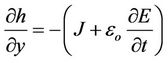 (7)
(7)
 (8)
(8)
Eliminating J between Equations (6) and (7) we obtain
 (9)
(9)
Eliminating E between Equations (8) and (9) we obtain
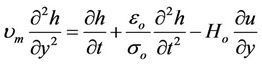 (10)
(10)
The Lorentz force has a non-vanishing component in the x-direction, given by:
 (11)
(11)
Assume that the viscoelastic fluid contains some chemically reactive diffusive species then the equations describing the flow in the boundary layer reduce to:
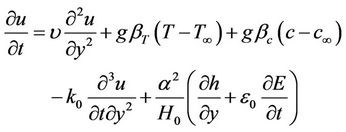 (12)
(12)
 (13)
(13)
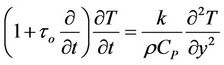 (14)
(14)
 (15)
(15)
 (16)
(16)
Introduce the non-dimensional quantities.
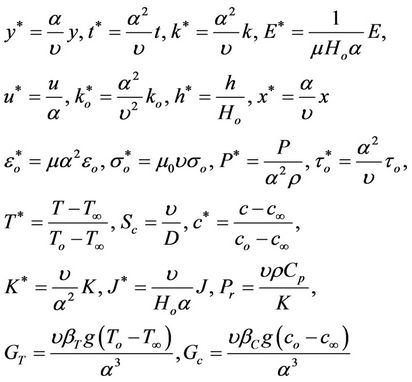 (17)
(17)
With the help of the non-dimensional quantities above Equations (12)-(16) reduced to the non-dimensional equations
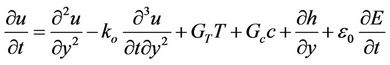 (18)
(18)
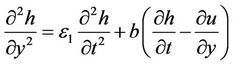 (19)
(19)
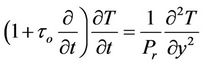 (20)
(20)
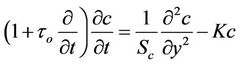 (21)
(21)
 (22)
(22)
where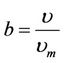 ,
, .
.
To simplify the algebra, only problems with zero initial conditions are considered. Taking Laplace transform of Equations (18)-(22) and writing the resulting equations in matrix form results in (23).
where




and
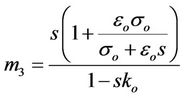 .
.
In Equation (23) the overbar denotes the Laplace transform and the prime indicates differentiations with respect to y.
 (23)
(23)
Equation (23) can be written in constracted form as
 (24)
(24)
The formal solution can be expressed as:
 (25)
(25)
The characteristic equation of the matrix 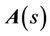 is
is
 (26)
(26)
where
 (27)
(27)
The roots ,
,  ,
,  and
and  of Equation (25) satisfy the relations:
of Equation (25) satisfy the relations:
 (28)
(28)
Two of the roots, say  and
and  have simple expression given by
have simple expression given by
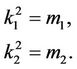 (29a)
(29a)
The other two roots  and
and  satisfy the relation
satisfy the relation
 (29b)
(29b)
The Maclaurin series expansion of  is given by
is given by
 .
.
Using the Cayley-Hamilton theorem, the infinite series can be truncated to the following form
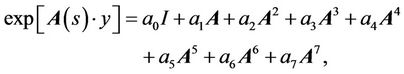 (30)
(30)
where I is the unit matrix of order 8 and a0 – a7 are some parameters depending on s and y.
The characteristic roots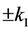 ,
,  ,
,  and
and  of the matrix A must satisfy the equations.
of the matrix A must satisfy the equations.




The solution of this system of linear equations is given in Appendix A:
Substituting for the parameters a0 - a7 into Equation (30) and computing A2, A3, A4, A5, A6 and A7, we get, the elements (ℓij i, j = 1, 2, 3, 4, 5, 6, 7, 8) of the matrix L(y, s) which listed in Appendix B.
It should be noted here that, we have used Equation (29) in order to write these entries in the simplest possible form. It should also be noted that this is a formal expression for the matrix exponential. In the physical problem , we should suppress the positive exponential which are unbounded at infinity. Thus we should replace each
, we should suppress the positive exponential which are unbounded at infinity. Thus we should replace each  by
by  and each
and each  by
by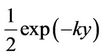 .
.
It is now possible to solve broad class problems in the Laplace transform domain.
3. Thermal Shock-Chemical Reactive Problem
Consider the free convection flow of an incompressible viscoelastic fluid in the presence of magnetic field occupying a semi-infinite region y ³ 0 of the space bounded by an infinite vertical plate y = 0 with quiescent initial state. A thermal-concentration shock is applied to the boundary plane y = 0 in the form
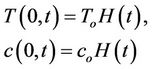 (31)
(31)
and the mechanical boundary conditions on the plate is taken as
 (32)
(32)
where  and
and  are constant and H(t) is Heaviside unit step function.
are constant and H(t) is Heaviside unit step function.
Now we apply the state space approach described above to this problem.
Since the solution is bounded at infinity, then the expressions for 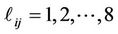 can be obtained by suppressing the positive exponential terms in Equation (30) which are not bounded at infinity. Thus for
can be obtained by suppressing the positive exponential terms in Equation (30) which are not bounded at infinity. Thus for , we should replace each
, we should replace each  by
by  and each
and each  by
by .
.
The components of the transformed initial state vector  are known name
are known name
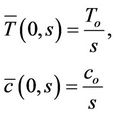 (33)
(33)
 (34)
(34)
In order to obtain the remaining four components ,
,  ,
,  and
and  we substitute y = 0 into Equations (31) and (32) to obtain the following linear system of equations:
we substitute y = 0 into Equations (31) and (32) to obtain the following linear system of equations:
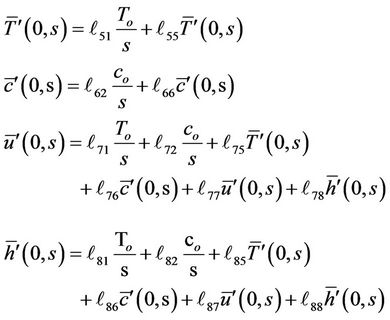 (35)
(35)
By solving this system, we arrive at
 (36)
(36)
Finally substituting the above value into (25), we obtain the solution of the problem in the transformed domain as:
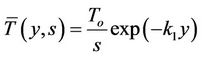 (37)
(37)
 (38)
(38)
 (39)
(39)
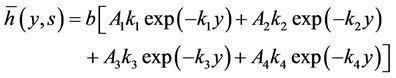 (40)
(40)
where the constants Ai, i = 1, 2, 3, 4 are listed in Appendix C.
The induced electric field and current density take the following forms
 (41)
(41)
 (42)
(42)
The shearing stress at the wall is given by
 (43)
(43)
4. Inversion of the Laplace Transforms
In order to invert the Laplace transform in the above equations, we adopt a numerical inversion method based on a Fourier series expansion [11]. In this method, the inverse g(t) of the Laplace transform 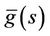 is approximated by the relation
is approximated by the relation
 (44)
(44)
where N is a sufficiently large integer representing the number of terms in the truncated infinite Fourier series. N must chosen such that
 where
where  is a persecuted small positive number that corresponds to the degree of accuracy to be achieved. The parameter c is a positive free parameter that must be greater than the real parts of all singularities of
is a persecuted small positive number that corresponds to the degree of accuracy to be achieved. The parameter c is a positive free parameter that must be greater than the real parts of all singularities of . The optimal choice of c was obtained according to the criteria described in [11].
. The optimal choice of c was obtained according to the criteria described in [11].
5. Numerical Results and Discussion
The problem of free convective flow with heat and mass transfer of a viscous incompressible viscoelastic electrically conducting fluid past a vertical plate in presence of a transverse magnetic field has been considered. The solutions for velocity, temperature and concentration fields as well as the induced magnetic and electric fields are obtained by using the state space approach. The technique is applied to a thermal shock-chemical reactive problem without heat sources. The effects of flow parameters such as Grashof number for heat and mass transfer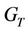 ,
,  , Prandtl number
, Prandtl number , Schmidt number
, Schmidt number , chemical reaction parameter K, viscoelastic parameter
, chemical reaction parameter K, viscoelastic parameter 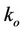 and relaxation time
and relaxation time 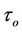 have been studied analytically and presented with the help of Figures 1-8 for the considered problem.
have been studied analytically and presented with the help of Figures 1-8 for the considered problem.
5.1. Velocity Field (u)
The velocity of the flow field varies vastly with the variation of the flow parameters such as Grashof number for heat and mass transfer ,
,  , viscoelastic parameter
, viscoelastic parameter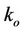 , Prandtl number
, Prandtl number , Schmidt number
, Schmidt number , chemical reaction parameter K. The effects of these parameters on the velocity fluid of flow field have been presented in Figures 1-3.
, chemical reaction parameter K. The effects of these parameters on the velocity fluid of flow field have been presented in Figures 1-3.
5.1.1. Effect of Viscoelastic Parameter (ko)
Figure 1 depicts the effect of viscoelastic parameter  on the velocity profiles of the flow field keeping other parameters of the flow field constant. The curve with viscoelastic parameter,
on the velocity profiles of the flow field keeping other parameters of the flow field constant. The curve with viscoelastic parameter,  corresponds to Newtonian flow and in other two curves the viscoelastic parameter is taken in increasing order. The viscoelastic parameter is found to decelerate the velocity of the flow field. The above parameter is in good agreement with the result obtained in cases of Khan and Sanjayanand [10].
corresponds to Newtonian flow and in other two curves the viscoelastic parameter is taken in increasing order. The viscoelastic parameter is found to decelerate the velocity of the flow field. The above parameter is in good agreement with the result obtained in cases of Khan and Sanjayanand [10].
5.1.2. Effect of Grashof Number for Heat (GT)
The values of Grashof number for heat  have been chosen as they are interesting from physical point of view. The free convection of heat is due to the temperature difference
have been chosen as they are interesting from physical point of view. The free convection of heat is due to the temperature difference  and hence
and hence  when
when  which physically corresponds to cooling of the surface by free convection currents. Then
which physically corresponds to cooling of the surface by free convection currents. Then  correspond to heating of the surface by free convection currents. In Figure 2, we observe that the effect of cooling and heating by free convection currents when
correspond to heating of the surface by free convection currents. In Figure 2, we observe that the effect of cooling and heating by free convection currents when  and
and  are in agreement with physical observations that cooling of the surface by free convection currents occurs for positive values of
are in agreement with physical observations that cooling of the surface by free convection currents occurs for positive values of  while heating corresponds to negative values of
while heating corresponds to negative values of . It was also noticed that the velocity increase with the increase of
. It was also noticed that the velocity increase with the increase of .
.
5.1.3. Effect of Different Parameters (Gc, Pr, Sc, K)
Figure 3 present the effect of Grashof number for mass transfer , Prandtl number
, Prandtl number , Schmidt number
, Schmidt number 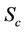 and chemical reaction parameter K on the velocity profiles of the flow fluid. Comparing the curve (1) and (2) of the figure, it is observed that the Grashof number for mass transfer is to enhance the velocity of the flow field at all points. The effect of both Prandtl number
and chemical reaction parameter K on the velocity profiles of the flow fluid. Comparing the curve (1) and (2) of the figure, it is observed that the Grashof number for mass transfer is to enhance the velocity of the flow field at all points. The effect of both Prandtl number  and chemical reaction parameter K on the velocity field is shown by the curves (1), (3) and (5). It was found that the increasing of
and chemical reaction parameter K on the velocity field is shown by the curves (1), (3) and (5). It was found that the increasing of  and K lead to decelerate the velocity of the flow field. Curves (1) and (4) describe the effect of Schmidt number
and K lead to decelerate the velocity of the flow field. Curves (1) and (4) describe the effect of Schmidt number  on the velocity profiles of the flow field which reveal that the presence of heavier diffusing species has a retarding effect on the velocity of the flow field. The effect of the above parameters has the same behavior as in case of Das et al. [13].
on the velocity profiles of the flow field which reveal that the presence of heavier diffusing species has a retarding effect on the velocity of the flow field. The effect of the above parameters has the same behavior as in case of Das et al. [13].
5.2. Temperature Field (T)
The temperature field is found to change more or less with the variation of the Prandtl number . Figure 4 is plot of non-dimensional temperature and distance for five different values of the Prandtl number. The temperature
. Figure 4 is plot of non-dimensional temperature and distance for five different values of the Prandtl number. The temperature

Figure 1. Velocity distribution for different values of viscoelastic parameter ko.

Figure 2. Velocity distribution for different values of GT.

Figure 3. Velocity distribution for different values of Gc, Pr, Sc and K.
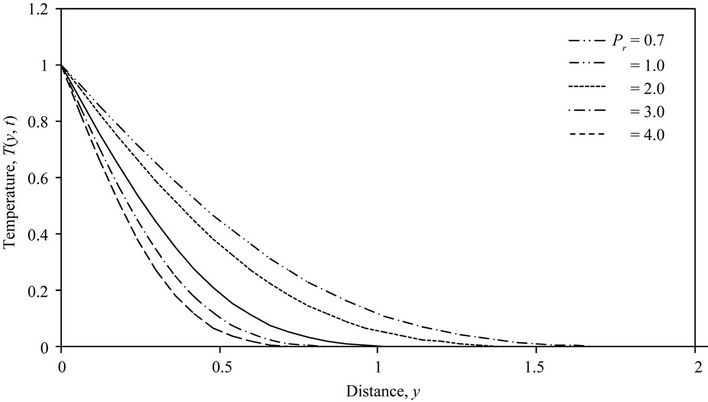
Figure 4. Temperature distribution for different values of Pr.

Figure 5. Concentration distribution for different values of Sc.
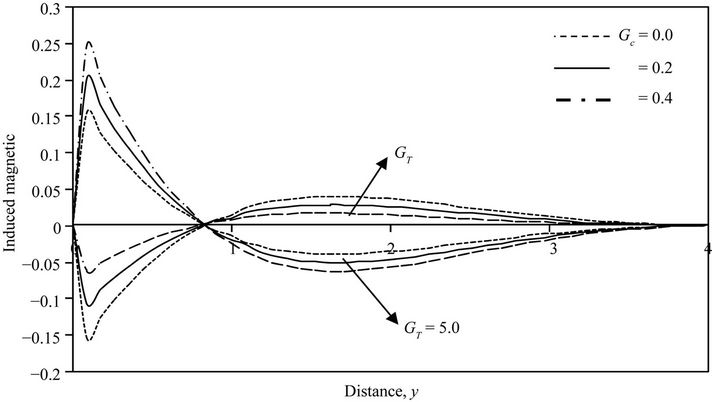
Figure 6. Induced magnetic field distribution for different values of GT, Gc.
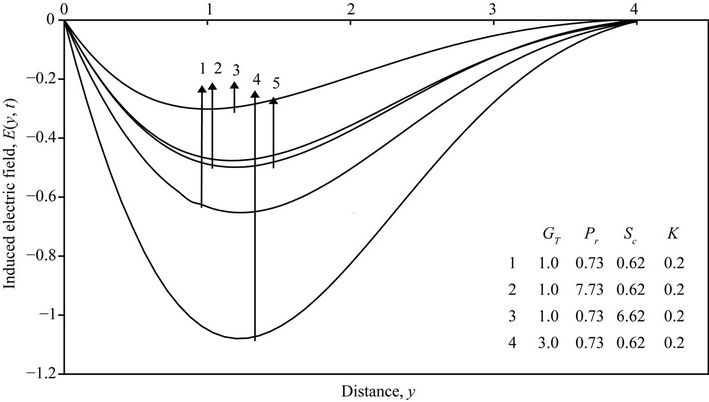
Figure 7. Induced electric field distribution for different values of GT, Pr, Sc and K.

Figure 8. Current density distribution for different values of GT, Pr, Sc and K.
of the flow field diminishes as the Prandtl number increases. Higher the Prandtl number, the sharper is the reduction in the temperature of the flow field.
5.3. Concentration Field (c)
The variation of the concentration distribution of the flow field with the diffusion of the mass is shown in Figure 5. The concentration distribution decreases at all points of the flow field with the increase of the Schmidt number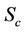 . This shows that the heavier the diffusing species have a greater retarding effect on the concentration distribution of the flow field. The concentration profiles are in good agreement with the results obtained in case of Hsiao [14].
. This shows that the heavier the diffusing species have a greater retarding effect on the concentration distribution of the flow field. The concentration profiles are in good agreement with the results obtained in case of Hsiao [14].
5.4. Induced Magnetic Field (h)
Figure 6 concentrate on variations in the induced magnetic field profiles h for cooling  and heating
and heating  of the plate due to change in the values of Grashof number for mass transfer
of the plate due to change in the values of Grashof number for mass transfer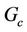 . It is observed that for cooling (heating) of the plate the induced magnetic field increases (decreases) rapidly in the vicinity of the plate and decreases (increases) asymptotically for higher values of y. It is also observed that an increase in Grashof number for mass transfer
. It is observed that for cooling (heating) of the plate the induced magnetic field increases (decreases) rapidly in the vicinity of the plate and decreases (increases) asymptotically for higher values of y. It is also observed that an increase in Grashof number for mass transfer  increases (decreases) the induced magnetic field.
increases (decreases) the induced magnetic field.
5.5. Induced Electric Field (E) and Current Density (J)
The induced electric field and current density of the flow field vary vastly with the variation of the flow parameters such as Grashof number , Prandtl number
, Prandtl number , Schmidt number
, Schmidt number  and chemical reaction parameter K. The effects of these parameters on the induced electric field and current density have been presented in Figures 7 and 8.
and chemical reaction parameter K. The effects of these parameters on the induced electric field and current density have been presented in Figures 7 and 8.
Effect of Different Parameters (GT, Pr, Sc, K)
Figures 7 and 8 present the effect of Grashof number for heat transfer , Prandtl number
, Prandtl number , Schmidt number
, Schmidt number  and chemical reaction parameter K on the induced electric field E, and current density J profiles of the flow fluid, respectively. It was found that the increasing of these parameters lead to decelerate the magnitude of both the induced magnetic field and current density but Grashof number for heat transfer is to enhance them.
and chemical reaction parameter K on the induced electric field E, and current density J profiles of the flow fluid, respectively. It was found that the increasing of these parameters lead to decelerate the magnitude of both the induced magnetic field and current density but Grashof number for heat transfer is to enhance them.
5.6. Skin Friction (τ)
The numerical values of skin friction coefficient τ for different values of ,
, 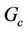 ,
, 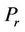 ,
,  , K and
, K and  corresponding to cooling of the plate
corresponding to cooling of the plate 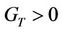 are entered in Table 1. It is observed that the skin friction coefficient τ increases due to increase in
are entered in Table 1. It is observed that the skin friction coefficient τ increases due to increase in ,
,  while decrease due to increase in
while decrease due to increase in ,
,  , K and
, K and .
.
6. Concluding Remarks
1) Owing to the complicated nature of the governing equations for the unsteady MHD viscoelastic flow, few attempts have been made to solve problems in this field. These attempts utilized approximate methods valid for only a specific range of some parameters. In this work, the method of direct integration by means of the matrix exponential, which is a standard approach in modern control theory and is developed in detail in many texts such as Ezzat [1], is introduced in the field of MHD and is applied to specific problems in which the temperature, velocity, concentration and magnetic field are coupled. This method gives exact solutions in the Laplace transform

Table 1. Values of the skin friction τ due to the variation of GT, Gc, Pr, Sc, K and ko.
domain without any assumed restrictions on the applied magnetic field or viscoelastic parameters. The same approach was used quite successfully in dealing with problems in generalized thermoelasticity theory by Ezzat et al. [15].
2) In this work, we use a more general model of equations, which includes the relaxation time of heat conduction 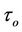 and the electric permeability of the electromagnetic field
and the electric permeability of the electromagnetic field . The inclusion of the relaxation time and electric permeability modifies the governing thermal, concentration and electromagnetic equations, changing them from parabolic to hyperbolic type, and thereby eliminating the unrealistic result that thermal and chemical reactive disturbance is realized instantaneously everywhere within a fluid.
. The inclusion of the relaxation time and electric permeability modifies the governing thermal, concentration and electromagnetic equations, changing them from parabolic to hyperbolic type, and thereby eliminating the unrealistic result that thermal and chemical reactive disturbance is realized instantaneously everywhere within a fluid.
3) The work considered here in reflects the effects of transverse magnetic field and chemical reaction on an unsteady laminar incompressible free convection heat and mass transfer flow of a viscoelastic fluid past an infinite vertical plate. A set of linear differential equations governing the fluid velocity, temperature, species concentration and induced magnetic field is solved by the method of state space approach. The parameters that arise in this analysis are prandtl number  (thermal diffusivity), Schmidt number
(thermal diffusivity), Schmidt number  (mass diffusivity), thermal Grashof number
(mass diffusivity), thermal Grashof number 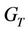 (free convection), Solutal Grashof number
(free convection), Solutal Grashof number , chemical reaction parameter K and viscoelastic parameter
, chemical reaction parameter K and viscoelastic parameter . A comprehensive set of graphical results for the velocity, temperature, concentration, induced magnetic and electric field and current density is presented and discussed.
. A comprehensive set of graphical results for the velocity, temperature, concentration, induced magnetic and electric field and current density is presented and discussed.
4) The flow of fluids over the boundaries has many applications such as boundary-layer control. The study of unsteady boundary layers owes its importance to the fact that all boundary layers that occur in real life are, in a sense, unsteady. In recent years, the requirements of modern technology have stimulated interest in fluid-flow studies, which involve the intersection of several phenomena. One such study is related to the effects of free convection flow through, which play an important role in agriculture, engineering, petroleum industries, and heat transfer.
REFERENCES
- M. A. Ezzat, “State Space Approach to Solids and Fluids,” Canadian Journal of Physics Review, Vol. 86, No. 11, 2008, pp. 1242-1250. doi:10.1139/P08-069
- E. Scribben, D. Baird and P. Wapperom, “The Role of Transient Rheology in Poly-Meric Sintering,” Rheologica Acta, Vol. 45, No. 6, 2006, pp. 825-839.
- Z. Wouter, M. Hendriks and M. T. Hart, “A VelocityBased Approach to Visco-Elastic Flow of Rock,” Mathematical Geology, Vol. 37, 2005, pp. 141-162.
- B. O. Anwar and O. D. Makinde, “Viscoelastic Flow and Species Transfer in a Darcian High-Permeability Channel,” Journal of Petroleum Science and Engineering, Vol. 76, No. 3-4, 2011, pp. 93-97. doi:10.1016/j.petrol.2011.01.008
- Y. Xia and A. M. Jacobi, “Air-Side Data Interpretation and Performance Analysis for Heat Exchangers with Simultaneous Heat and Mass Transfer, Wet and Frosted Surfaces,” International Journal of Heat and Mass Transfer, Vol. 48, No. 25-26, 2005, pp. 5089-5102. doi:10.1016/j.ijheatmasstransfer.2005.08.008
- M. A. Ezzat and M. Zakaria, “Heat Transfer with Thermal Relaxation to a Perfectly Conducting Polar Fluid,” Heat and Mass Transfer, Vol. 41, No. 3, 2005, pp. 189- 198. doi:10.1007/s00231-004-0511-y
- H. I. Andersson, “MHD Flow of a Viscoelastic Fluid past a Stretching Surface,” Acta Mechanica, Vol. 95, No. 1-4, 1992, pp. 227-230.
- B. C. Sakiadis, “Boundary Layer Behavior on Continuous Solid Surface: Part II. The Boundary Layer on a Continuous Flat Surface,” AIChE Journal, Vol. 7, No. 2, 1961, pp. 221-225.
- M. A. Ezzat and M. Zakaria, “State Space Approach to Viscoelastic Fluid Flow of Hydromagnetic Fluctuating Boundary-Layer through a Porous Medium,” ZAMM, Vol. 77, 1997, pp. 197-207.
- S. K. Khan and E. Sanjayanand, “Viscoelastic Boundary Layer Flow and Heat Transfer over an Exponential Stretching Sheet,” International Journal of Heat and Mass Transfer, Vol. 48, No. 8, 2005, pp. 1534-1542. doi:10.1016/j.ijheatmasstransfer.2004.10.032
- G. Honig and U. Hirdes, “A method for the Numerical Inversion of Laplace Transforms,” Computational and Applied Mathematics, Vol. 10, No. 1, 1984, pp. 113-132.
- M. A. Ezzat, “Free Convection Effects on Perfectly Conducting Fluid,” International Journal of Engineering Science, Vol. 39, No. 7, 2001, pp. 799-819. doi:10.1016/S0020-7225(00)00059-8
- S. Das, A. Satapathy, J. Das and J. Panda, “Mass Transfer Effects on MHD Flow and Heat Transfer Past a Vertical Porous Plate through a Porous Medium Under Oscillatory Suction and Heat Source,” International Journal of Heat and Mass Transfer, Vol. 52, No. 25-26, 2009, pp. 5962- 5969. doi:10.1016/j.ijheatmasstransfer.2009.04.038
- K. L. Hsiao, “Heat and Mass Mixed Convection for MHD Visco-Elastic Fluid Past a Stretching Sheet with Ohmic dissipation,” Communications in Nonlinear Science and Numerical Simulation, Vol. 15, No. 7, 2010, pp. 1803- 1812. doi:10.1016/j.cnsns.2009.07.006
- M. A. Ezzat, M. I. Othman and A. A. Smaan, “State Space Approach to Two-Dimensional Electro-Magneto Thermoelastic Problem with Two Relaxation Times,” International Journal of Engineering Science, Vol. 39, 2001, pp. 1383-1404. doi:10.1016/S0020-7225(00)00095-1.
Appendix A: The Solution of the Linear System
 ,
, 




 ,
, 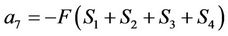
where

 ,
, 
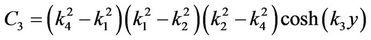 ,
, 
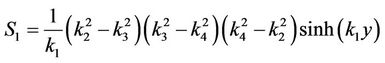 ,
, 
 ,
, 
Appendix B: Elements of the Matrix L(s, y)
 ,
,  ,
,  ,
, 
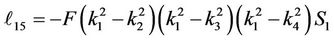 ,
,  ,
, 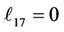 ,
,  ,
, 
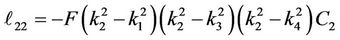 ,
,  ,
,  ,
,
 ,
,  ,
, 




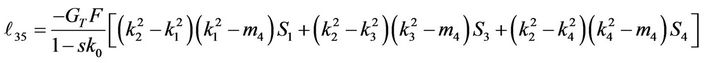


 ,
,




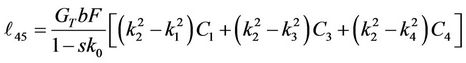 ,
,
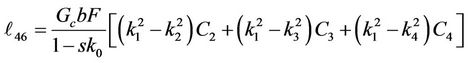


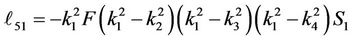 ,
, 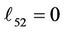 ,
, 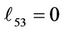 ,
, 
 ,
,  ,
,  ,
,  ,
, 
 ,
,  ,
, 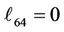 ,
, 
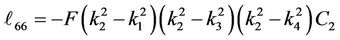 ,
,  ,
, 









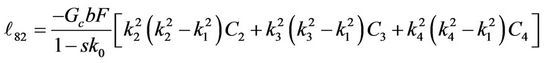


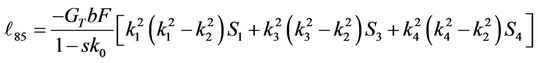



Appendix C: The Constants for the Problem
 ,
, 

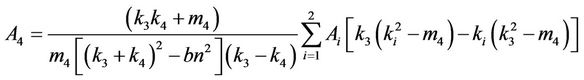 .
.
Nomenclature
 density
density
 time
time
 space coordinates
space coordinates
 velocity vector
velocity vector
 magnetic field intensity vector
magnetic field intensity vector
 magnetic induction vector
magnetic induction vector
 electric induction vector
electric induction vector
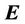 induced electric field vector
induced electric field vector
 induced magnetic field vector
induced magnetic field vector
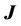 conduction electric density vector
conduction electric density vector
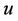 velocity of the fluid along the x-direction
velocity of the fluid along the x-direction
 temperature
temperature
 concentration
concentration
 mass diffusivity of chemically reactive species
mass diffusivity of chemically reactive species
 chemical reaction parameter
chemical reaction parameter
 acceleration
acceleration
 temperature of the fluid away from the surface
temperature of the fluid away from the surface
 concentration of the fluid away from the surface
concentration of the fluid away from the surface
 specific heat at constant pressure
specific heat at constant pressure
 viscoelastic parameter
viscoelastic parameter
 thermal Grashof number
thermal Grashof number
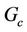 solute Grashof number
solute Grashof number
 Prandtl number
Prandtl number
 Schmidt number
Schmidt number
 constant component of magnetic field
constant component of magnetic field
 electrical conductivity
electrical conductivity
 magnetic permeability
magnetic permeability
 thermal conductivity
thermal conductivity
 dynamic viscosity
dynamic viscosity

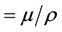 , kinematics viscosity
, kinematics viscosity
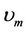
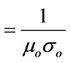 , magnetic diffusivity
, magnetic diffusivity
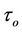 thermal relaxation time
thermal relaxation time

 , Alfven velocity
, Alfven velocity
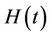 Heaviside unit step function
Heaviside unit step function
NOTES
*Corresponding author.

