International Journal of Astronomy and Astrophysics
Vol.3 No.4(2013), Article ID:38393,4 pages DOI:10.4236/ijaa.2013.34042
Redshift Independence of the Amati and Yonetoku Relations for Gamma-Ray Bursts
Department of Physics, College of Science, University of Bahrain, Sakhir, Kingdom of Bahrain
Email: wjazzam@uob.edu.bh, wjazzam@gmail.com
Copyright © 2013 Walid J. Azzam, Mohamed J. Alothman. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received August 28, 2013; revised September 24, 2013; accepted September 30, 2013
Keywords: Gamma-Ray Bursts; Energy Correlations; Luminosity Indicators; Redshift Evolution
ABSTRACT
The Amati and Yonetoku relations are two of the main energy and luminosity correlations that currently exist for gamma-ray bursts (GRBs). The Amati relation is a correlation between the intrinsic peak energy, Epeak, in the nFn spectrum of a burst and its equivalent isotropic energy, Eiso. The Yonetoku relation is a correlation between Epeak and the isotropic peak luminosity, Liso. In this paper, we use a recent data sample of 65 GRBs to investigate whether these two relations evolve with redshift, z. The z-correction and the k-correction are both taken into account. Our method consists of binning the data in redshift, z, then applying (for each bin) a fit of the form:  for the Amati relation, and of the form:
for the Amati relation, and of the form:  for the Yonetoku relation, where áEpeakñ is the mean value of the peak energy for the entire sample. The objective is to see whether the two fitting parameters, A and B, evolve systematically with z. Good least-squares fits were obtained with reasonable values for the linear regression coefficient, r. Our results indicate that the normalization, A, and the slope, B, do not evolve with redshift, and hence the Amati and Yonetoku relations seem to be redshift independent.
for the Yonetoku relation, where áEpeakñ is the mean value of the peak energy for the entire sample. The objective is to see whether the two fitting parameters, A and B, evolve systematically with z. Good least-squares fits were obtained with reasonable values for the linear regression coefficient, r. Our results indicate that the normalization, A, and the slope, B, do not evolve with redshift, and hence the Amati and Yonetoku relations seem to be redshift independent.
1. Introduction
There are currently several energy and luminosity correlations for gamma-ray bursts (GRBs). Some were obtained from the light curves, like the lag-luminosity and variability relations [1,2], while others were obtained from the spectra and included the Amati relation [3-6], the Ghirlanda relation [7], the Yonetoku relation [8,9], and the Liang-Zhang relation [10]. The importance of these correlations resides in their potential use as cosmological probes that might help constrain cosmological models [11-15], and also as tools that might help probe the physics of GRBs.
On the other hand, some studies have looked at possible inherent problems that these relations might suffer from, like the circularity problem and selection effects [16-20]. However, less attention has been given to the possible redshift evolution of these correlations as evidenced by the few studies dedicated specifically to this issue [21-26]. But since these relations are typically calibrated over a wide range in redshift (roughly 0.1 < z < 8), it becomes incumbent to study their possible dependence on z, if they are to be utilized as cosmological probes.
The purpose of this paper is to investigate the possible redshift evolution of two well-known GRB energy and luminosity correlations—namely, the Amati and Yonetoku relations. The Amati relation is a correlation between the intrinsic (i.e., rest-frame) peak energy, Epeak, in a burst’s nFn spectrum and its equivalent isotropic energy, Eiso. The Yonetoku relation, on the other hand, is a correlation between Epeak and a burst’s isotropic peak luminosity, Liso.
In this paper we study the possible redshift evolution of these two relations by making use of a recent data sample consisting of 65 GRBs. The data, analysis, and results are presented in Section 2, which is followed by a discussion and summary in Section 3.
2. Data, Analysis, and Results
The data sample used in this study is taken from Geng and Huang [27], who were able to fit the time-averaged spectra of 65 GRBs using the Band function and to extract the relevant spectrum parameters. The data sample includes bursts that were observed by Swift, Konus/Wind, or Fermi. The values for Eiso and Liso were obtained by integrating over the energy range 1 keV to 104 keV in the burst’s rest frame and applying the appropriate k-correction. Although the entire data sample consists of 65 GRBs, only 53 bursts have both Epeak and Eiso values available and so these are the bursts that we used in our analysis of the Amati relation; similarly, only 47 bursts have both Epeak and Liso values available and thus these are the bursts that we used in our analysis of the Yonetoku relation.
Our method consists of binning the data by redshift, then writing the Amati relation as:
 (1)
(1)
and the Yonetoku relation as:
 (2)
(2)
and then extracting the fit parameters A and B for each bin; the objective is to see whether A and B vary systematically with z. Note that we normalized Epeak to the corresponding mean value for the entire sample, áEpeakñ, in order to avoid introducing any spurious correlations between the two fit parameters.
The binning was done by fixing the number of bursts per redshift bin, and a different number of bins was tried in order to check that the binning itself does not affect our conclusions. Table 1 shows our results for the Amati relation when a least-squares fit was used with 5 bins. The first two columns show, respectively, the bin number and the mean redshift for that particular bin. Columns 3 and 4 show the best-fit values for A and B, respectively, along with their 1s errors. The values for the linear regression coefficient, r, and its corresponding chance probability, P, were also calculated and are shown in columns 5 and 6, respectively. Table 2 is similar to Table 1 but shows our results for the Yonetoku relation. Both tables show that the goodness of the fits varied
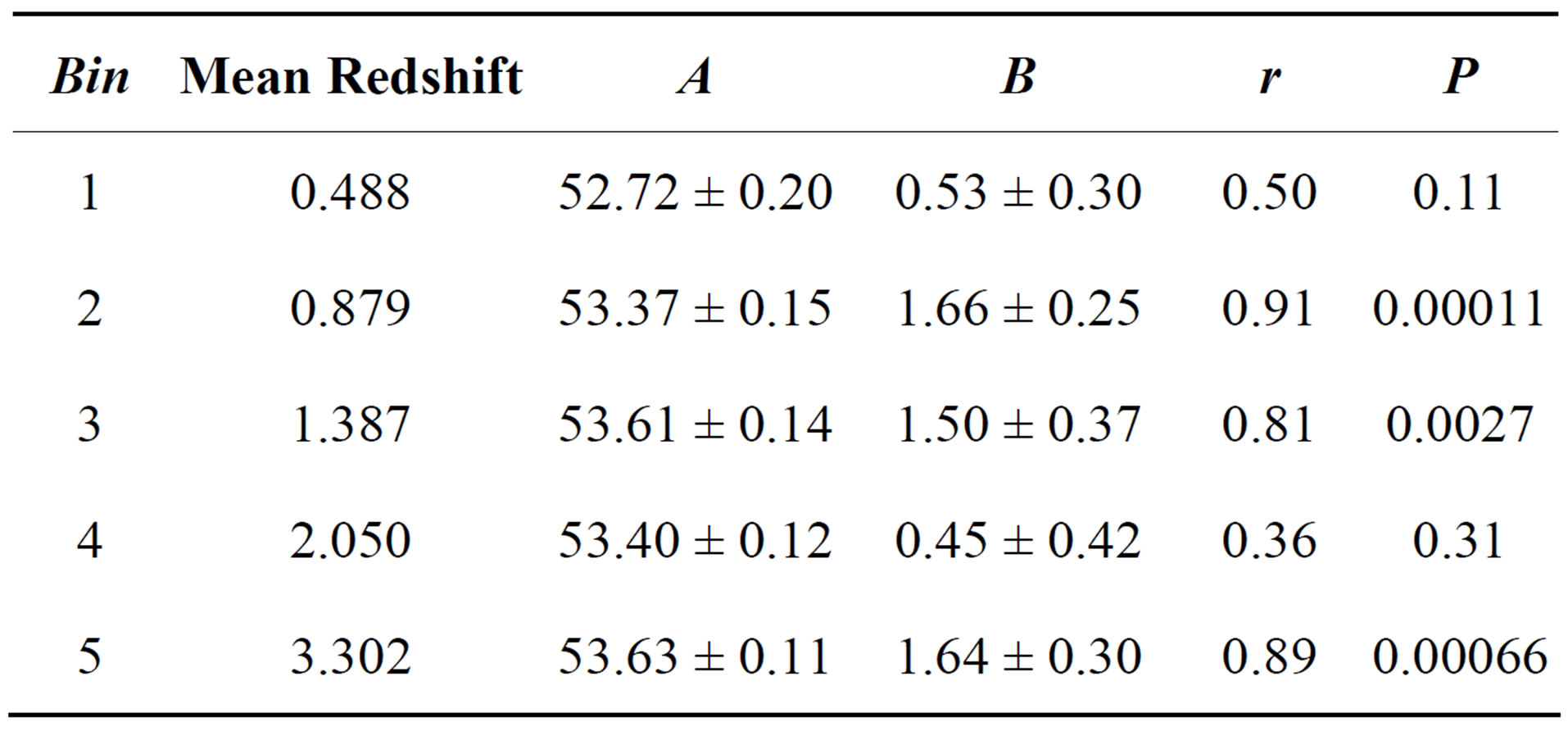
Table 1. The best-fit values for the normalization, A, and the slope, B, along with their 1 s errors, obtained for the Amati relation. The linear regression coefficient, r, and its corresponding chance probability, P, are also shown.
from bin to bin, with some bins having very good fits while others have acceptable fits, which is probably due to the paucity of data points. A quick examination of the two tables shows that neither shows any systematic trend between the fitting parameters, A and B, and the redshift.
Figure 1 shows the best-fit lines for the Amati relation and Figure 2 shows how the corresponding values for A

Table 2. The best-fit values for the normalization, A, and the slope, B, along with their 1 s errors, obtained for the Yonetoku relation. The linear regression coefficient, r, and its corresponding chance probability, P, are also shown.

Figure 1. The equivalent isotropic energy, Eiso, plotted versus the normalized rest-frame peak energy (the Amati relation) for different redshift bins, where Bin 1 represents the lowest redshift range.

Figure 2. The normalization, A, and the slope, B, plotted versus the mean redshift for the least-squares fits shown in Figure 1. The vertical bars refer to 1 s errors.
and B vary with redshift. In Figure 2, the vertical bars refer to 1s errors, and the exact horizontal location of the points was set at the mean redshift value for each bin. Figures 3 and 4 are similar to Figures 1 and 2, respectively, but for the Yonetoku relation. Figure 4 shows an initial rise in the values of A and B, but this is not significant since the values soon “saturate” and are consistent with one another to within 1 s. Therefore, the figures reinforce what is seen in the two tables—namely, the best-fit lines, and hence the fitting parameters, A and B, do not vary systematically with z.

Figure 3. The isotropic peak luminosity, Liso, plotted versus the normalized rest-frame peak energy (the Yonetoku relation) for different redshift bins, where Bin 1 represents the lowest redshift range.

Figure 4. The normalization, A, and the slope, B, plotted versus the mean redshift for the least-squares fits shown in Figure 3. The vertical bars refer to 1 s errors.
3. Discussion and Summary
In this section we would like to put our study in proper context by comparing it to what has been done by others. As mentioned earlier, although many recent studies have looked at different aspects of GRB energy and luminosity relations [27-29], only a few have specifically considered the issue of redshift evolution of these relations.
One of the earliest studies to look at this issue is the paper by [21] in which a sample of 48 GRBs was used to investigate the possible redshift evolution of the Amati relation. The author of that paper found evidence that this relation gets steeper with redshift, and thus concluded that the Amati relation seems to evolve with redshift. However, a subsequent investigation by [18] extended the study done by [21] by enlarging the data sample to 76 bursts. Although they confirmed the results found by [21] for the 48 bursts, when all 76 bursts were used the redshift evolution disappeared, and so their conclusion was that what [21] had found was probably due to low statistics. Our results are in agreement with what was found by [18] since no redshift evolution was found for either the Amati relation or the Yonetoku relation.
In conclusion, a data sample of 65 gamma-ray bursts was used to investigate the possible redshift evolution of the Amati and Yonetoku relations. Our analysis indicates that the normalization, A, and the slope, B, do not vary in a systematic way with z. Therefore, these two GRB relations seem to be redshift independent, and are thus robust in this regard.
REFERENCES
- J. P. Norris, et al., “Connection between Energy Dependent Lags and Peak Luminosity in Gamma-Ray Bursts,” The Astrophysical Journal, Vol. 534, No. 1, 2000, pp. 248-257. http://dx.doi.org/10.1086/308725
- E. E. Fenimore and E. Ramirez-Ruiz, “Redshifts for 220 BATSE Gamma-Ray Bursts Determined by Variability and the Cosmological Consequences,” astro-ph/0004176, 2000.
- L. Amati, et al., “Intrinsic Spectra and Energetics of BeppoSAX Gamma-Ray Bursts with Known Redshifts,” Astronomy and Astrophysics, Vol. 390, No. 1, 2002, pp. 81- 89. http://dx.doi.org/10.1051/0004-6361:20020722
- L. Amati, “The Ep,i-Eiso Correlation in Gamma-Ray Bursts: Updated Observational Status, Re-Analysis and Main Implications,” Monthly Notices of the Royal Astronomical Society, Vol. 372, No. 1, 2006, pp. 233-245. http://dx.doi.org/10.1111/j.1365-2966.2006.10840.x
- L. Amati, et al., “Measuring the Cosmological Parameters with the Ep,i-Eiso Correlation of Gamma-Ray Bursts,” Monthly Notices of the Royal Astronomical Society, Vol. 391, No. 2, 2008, pp. 577-584. http://dx.doi.org/10.1111/j.1365-2966.2008.13943.x
- L. Amati, et al., “Extremely Energetic Fermi Gamma-Ray Bursts Obey Spectral Energy Correlations,” Astronomy and Astrophysics, Vol. 508, No. 1, 2009, pp. 173-180. http://dx.doi.org/10.1051/0004-6361/200912788
- G. Ghirlanda, et al., “The Collimation-Corrected GammaRay Burst Energies Correlate with the Peak Energy of Their nFn Spectrum,” The Astrophysical Journal, Vol. 616, No. 1, 2004, pp. 331-338. http://dx.doi.org/10.1086/424913
- D. Yonetoku, et al., “Gamma-Ray Burst Formation Rate Inferred from the Spectral Peak Energy-Peak Luminosity Relation,” The Astrophysical Journal, Vol. 609, No. 2, 2004, pp. 935-951. http://dx.doi.org/10.1086/421285
- G. Ghirlanda, et al., “Spectral-Luminosity Relation within Individual Fermi Gamma-Ray Bursts,” Astronomy and Astrophysics, Vol. 511, 2010, pp. A43-A53. http://dx.doi.org/10.1051/0004-6361/200913134
- E. Liang and B. Zhang, “Model-Independent Multivariable Gamma-Ray Burst Luminosity Indicator and Its Possible Cosmological Implications,” The Astrophysical Journal, Vol. 633, No. 2, 2005, pp. L611-L623. http://dx.doi.org/10.1086/491594
- G. Ghirlanda, et al., “Cosmological Constraints with GRBs: Homogeneous vs. Wind Density Profile,” Astronomy and Astrophysics, Vol. 452, No. 3, 2006, pp. 839-844. http://dx.doi.org/10.1051/0004-6361:20054544
- S. Capozziello and L. Izzo, “Cosmography by GammaRay Bursts,” Astronomy and Astrophysics, Vol. 490, No. 1, 2008, pp. 31-36. http://dx.doi.org/10.1051/0004-6361:200810337
- M. Demianski and E. Piedipalumbo, “Standarizing the GRBs with the Amati Ep,i-Eiso Relation: The Updated Hubble Diagram and Implications for Cosmography,” Monthly Notices of the Royal Astronomical Society, Vol. 415, No. 4, 2011, pp. 3580-3590. http://dx.doi.org/10.1111/j.1365-2966.2011.18975.x
- W. J. Azzam and M. J. Alothman, “Constraining Cosmological Parameters through Gamma-Ray Bursts,” Advances in Space Research, Vol. 38, No. 7, 2006, pp. 1303-1306. http://dx.doi.org/10.1016/j.asr.2004.12.019
- W. J. Azzam and M. J. Alothman, “Gamma-Ray Burst Spectral-Energy Correlations as Cosmological Probes,” Il Nuovo Cimento B, Vol. 121, No. 12, 2006, pp. 1431-1432. http://dx.doi.org/10.1393/ncb/i2007-10270-5
- H. Li, et al., “Overcoming the Circular Problem for Gamma-Ray Bursts in Cosmological Global-Fitting Analysis,” The Astrophysical Journal, Vol. 680, No. 1, 2008, pp. 92-99. http://dx.doi.org/10.1086/529582
- N. R. Butler, et al., “Generalized Tests for Selection Effects in Gamma-Ray Burst High-Energy Correlations,” The Astrophysical Journal, Vol. 694, No. 1, 2009, pp. 76- 83. http://dx.doi.org/10.1088/0004-637X/694/1/76
- G. Ghirlanda, et al., “The Epeak-Eiso Plane of Long GammaRay Bursts and Selection Effects,” Monthly Notices of the Royal Astronomical Society, Vol. 387, No. 1, 2008, pp. 319-330. http://dx.doi.org/10.1111/j.1365-2966.2008.13232.x
- L. Nava, et al., “Selection Effects on GRB Spectral-Energy Correlations,” arXiv:0902.1522, 2009.
- C. Graziani, “GRBs as Standard Candles: There Is No ‘Circularity Problem’ (and There Never Was),” New Astronomy, Vol. 16, No. 2, 2011, pp. 57-64. http://dx.doi.org/10.1016/j.newast.2010.08.001
- L.-X. Li, “Variation of the Amati Relation with Cosmological Redshift: A Selection or an Evolution Effect?” Monthly Notices of the Royal Astronomical Society, Vol. 379, No. 1, 2007, pp. L55-L59. http://dx.doi.org/10.1111/j.1745-3933.2007.00333.x
- R. Tsutsui, et al., “Redshift-Dependent Lag-Luminosity Relation in 565 BATSE Gamma-Ray Bursts,” Monthly Notices of the Royal Astronomical Society, Vol. 386, No. 1, 2008, pp. L33-L37. http://dx.doi.org/10.1111/j.1745-3933.2008.00455.x
- W. J. Azzam, et al., “A Possible Redshift Evolution of the Time-Lag and Variability Luminosity Relations for Long Gamma-Ray Bursts,” Advances in Space Research, Vol. 44, No. 11, 2009, pp. 1354-1358. http://dx.doi.org/10.1016/j.asr.2009.08.003
- W. J. Azzam and H. A. Eid, “Variation of the Lag-Luminosity Relation with Redshift for Swift GRBs,” European Physical Journal Plus, Vol. 126, 2011, pp. 74-78. http://dx.doi.org/10.1140/epjp/i2011-11074-0
- W. J. Azzam and H. A. Eid, “Redshift Evolution of the Lag Relation for Swift GRBs,” AIP Conference Proceedings: Gamma-Ray Bursts, Vol. 1358, 2011, pp. 227-230. http://dx.doi.org/10.1063/1.3621777
- W. J. Azzam, “Dependence of the GRB Lag-Luminosity Relation on Redshift in the Source Frame,” International Journal of Astronomy and Astrophysics, Vol. 2, No. 1, 2012, pp. 1-5. http://dx.doi.org/10.4236/ijaa.2012.21001
- J. J. Geng and Y. F. Huang, “On the Correlations of Low-Energy Spectral Indices and Redshifts of GammaRay Bursts,” The Astrophysical Journal, Vol. 764, No. 1, 2013, pp. 75-83. http://dx.doi.org/10.1088/0004-637X/764/1/75
- Y. P. Qin and Z. F. Chen, “Roles of the Kinetic and Dynamic Mechanisms in the Lp-Ep Relation,” The Astrophysical Journal, Vol. 767, No. 1, 2013, pp. 2-8. http://dx.doi.org/10.1088/0004-637X/767/1/2
- R. Tsutsui, et al., “Possible Existence of the Ep-Lp and Ep-Eiso Correlations for Short Gamma-Ray Bursts with a Factor 5-100 Dimmer than Those for Long Gamma-Ray Bursts,” Monthly Notices of the Royal Astronomical Society, Vol. 431, No. 2, 2013, pp. 1398-1404. http://dx.doi.org/10.1093/mnras/stt262

