International Journal of Astronomy and Astrophysics
Vol.1 No.1(2011), Article ID:4373,4 pages DOI:10.4236/ijaa.2011.11002
Stability of Collinear Points in the Generalized Photogravitational Robes Restricted Three-Body Problem
Department of Mathematics Ahmadu Bello University Zaria, Nigeria
E-mail: raz11ng@yahoo.com
Received December 30, 2010; revised February 20, 2011; accepted February 23, 2011
Keywords: Stability, Collinear Points, Robes Problem, Density Parameters
Abstract
In studying the effects of radiation and oblateness of the primaries on the stability of collinear equilibrium points in the Robes restricted three-body problem we observed the variations of the density parameter k with the mass parameter μ for constant radiation and oblateness factors on the location and stability of the collinear points L1, L2 and L3. It is also discovered that the collinear points are unstable for k > 0 and stable for k < 0.
1. Introduction
The classical Restricted Three-Body problem has been generalized in various forms ([1,11,13,12,5-7,10,14]) by incorporating perturbing parameters such as perturbations in Coriolis and centrifugal forces, radiation pressure forces, oblateness of the primaries, drag effects and so on.
Robe [9] introduced a new kind of restricted three-body problem that incorporates the effect of buoyancy force. Here, one of the primaries is a rigid shell of mass filled with homogeneous incompressible fluid of density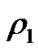 . The second primary
. The second primary 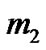 is a point mass located outside the shell. The third body
is a point mass located outside the shell. The third body 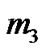 is the particle of negligible mass of density
is the particle of negligible mass of density 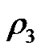 which moves inside the shell under the influences of the gravitational attraction of the primaries and the buoyancy force of the fluid of density
which moves inside the shell under the influences of the gravitational attraction of the primaries and the buoyancy force of the fluid of density . Robe studied the motion of the infinitesimal mass when
. Robe studied the motion of the infinitesimal mass when  describes both circular and elliptical orbits for
describes both circular and elliptical orbits for , obtained an equilibrium point at the centre of the shell and studied the linear stability of the point corresponding to the particular solution of the rotating system.
, obtained an equilibrium point at the centre of the shell and studied the linear stability of the point corresponding to the particular solution of the rotating system.
Recently, some forms of perturbations and other destabilizing parameters have been introduced to define new problems in Robes problem. Shrivastava and Garain [12] studied the effect of small perturbations in the Coriolis and centrifugal forces on the location of equilibrium points in the Robes problem. Plastino and Plastino [8] considered the Robes problem when the shape of the rigid shell is taken as Roche’s ellipsoid to study the linear stability of the equilibrium solutions. Giordano et al. [2] discussed the effect of drag force on the existence and stability of the equilibrium points in the Robes problem. Hallan and Rana [3] studied the existence of equilibrium points in the Robes problem and established that there exists one equilibrium in the Robes elliptical problem while the Robes circular problem has many equilibrium points. Hallan and Rana [4] studied the effect of oblateness on the location and stability of equilibrium points in the Robes circular problem when the primary other than the elliptical shell is oblate spheroid and proved that the center of the first primary is always an equilibrium point for all values of the density parameter k and the mass parameter μ.
Robes model is important for studying and understanding the problem of small oscillation that takes place within the core of a planet.
In our model, we consider a rigid shell which is oblate spheroid and the second primary radiating to study the stability of collinear equilibrium points in Robes restricted three-body problem while observing the variation of the location of the collinear points with the density parameter k and the mass parameter μ.
2. Equations of Motion
Let the mass of the rigid shell and the second primary be  and
and  respectively. Let the density of the incompressible fluid inside the shell be
respectively. Let the density of the incompressible fluid inside the shell be  and that of the infinitesimal mass moving inside the shell be
and that of the infinitesimal mass moving inside the shell be  and its mass. Let A denote the oblateness coefficient of the first primary such that
and its mass. Let A denote the oblateness coefficient of the first primary such that  and
and  the radiation force of the second primary, which is given by
the radiation force of the second primary, which is given by  such that
such that .
.
Let 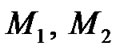 and
and 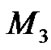 be the centers of m1, m2, and m3 respectively such that
be the centers of m1, m2, and m3 respectively such that  and
and . Let G be the gravitational constant and
. Let G be the gravitational constant and  the coordinates of the infinitesimal mass m. Further, we suppose that the line joining m1and m2 is the x-axis. The total potential acting at m is
the coordinates of the infinitesimal mass m. Further, we suppose that the line joining m1and m2 is the x-axis. The total potential acting at m is
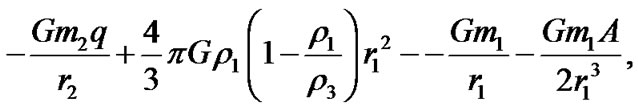
where

The coordinates m1 and m2 are  and
and  respectively. In dimensionless rotational coordinate system, we choose the unit of mass to be the sum of the masses of the primaries, i.e.
respectively. In dimensionless rotational coordinate system, we choose the unit of mass to be the sum of the masses of the primaries, i.e.  and
and . The unit of length is taken as equal to the distance between the primaries, and the unit is chosen so that
. The unit of length is taken as equal to the distance between the primaries, and the unit is chosen so that .
.
The equations of motion of the infinitesimal body are
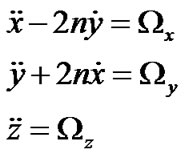 (1)
(1)
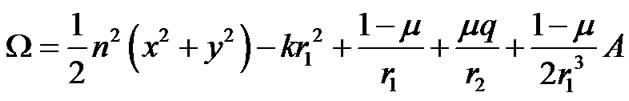 (2)
(2)
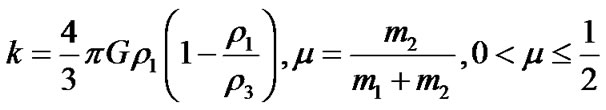
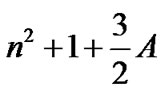 (3)
(3)
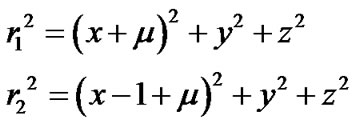 (4)
(4)
3. Equilibrium Points
Equilibrium points exist for the system when

For  (i.e.
(i.e.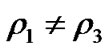 )
)
 (5)
(5)
 (6)
(6)
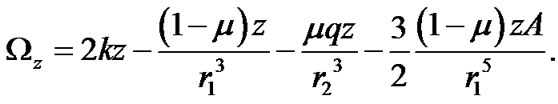 (7)
(7)
4. Collinear Points
Collinear equilibrium points occur when
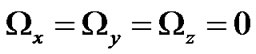 and
and 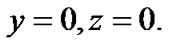
The equation
 (8)
(8)
gives the positions of the collinear points. We observe that

 and
and 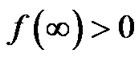 so that the collinear points L1, L2 and L3 lie in the intervals (μ,∞), (μ-1,μ) and (-∞,μ-1) respectively.
so that the collinear points L1, L2 and L3 lie in the intervals (μ,∞), (μ-1,μ) and (-∞,μ-1) respectively.
For L1, put ,
,  and substituting these values of r1 and r2 in Equation (8), putting
and substituting these values of r1 and r2 in Equation (8), putting  we obtain
we obtain
 (9)
(9)
This is a seventh degree algebraic equation in . For both positive and negative values of k there is only one change of sign in the equation. This shows the existence of at least one real root. Similarly, we have for L2 and L3
. For both positive and negative values of k there is only one change of sign in the equation. This shows the existence of at least one real root. Similarly, we have for L2 and L3
 (10)
(10)
and
 (11)
(11)
where 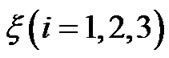 are given by Equations (9), (10) and (11) respectively for
are given by Equations (9), (10) and (11) respectively for  and
and . Therefore, the three collinear points are located as
. Therefore, the three collinear points are located as

Using MATLAB we generated real roots  of the Equations (9), (10) and (11) respectively to compute the respective values
of the Equations (9), (10) and (11) respectively to compute the respective values 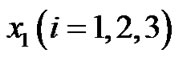 of the collinear points.
of the collinear points.
For constant values of the oblateness factor A and the radiation factor q, there is only one real root of (9) for each = 0,1,3,5 and μ = 0.1,0.2,0.3,0.4,0.5, three real roots of (10) and (11) except for k=1 where there are five distinct real roots in the case of Equation (11).
The variation in values of for various values of the density parameter k and mass parameter μ is shown in Figures 1, 2 and 3 respectively.
In Figures 1-3, the curve k = 0 corresponds to . That is, when the density of the fluid in the rigid shell is same as the density of the infinitesimal mass moving in the shell. The other curves, and correspond to the case when k = 1, k = 3, k = 5 correspond to the case when
. That is, when the density of the fluid in the rigid shell is same as the density of the infinitesimal mass moving in the shell. The other curves, and correspond to the case when k = 1, k = 3, k = 5 correspond to the case when .
.
5. Stability of Collinear Points
Let the equilibrium points and their positions be denoted by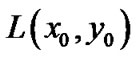 .Then we substitute
.Then we substitute
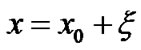 and
and 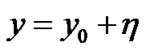 (12)
(12)
into the equations of motion (1) and obtain the equations of variation as
 (13)
(13)
where  and
and 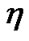 are small displacement in x0 and y0 respectively. Retaining only linear terms in
are small displacement in x0 and y0 respectively. Retaining only linear terms in  and
and  the characteristic Equations of (13) is
the characteristic Equations of (13) is
 (14)
(14)
where the superscripts indicate that the partial derivatives of 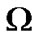 are to be evaluated at the equilibrium points
are to be evaluated at the equilibrium points 

Figure 1. Variation of location of L1 with density parameter k and mass parameter μ.
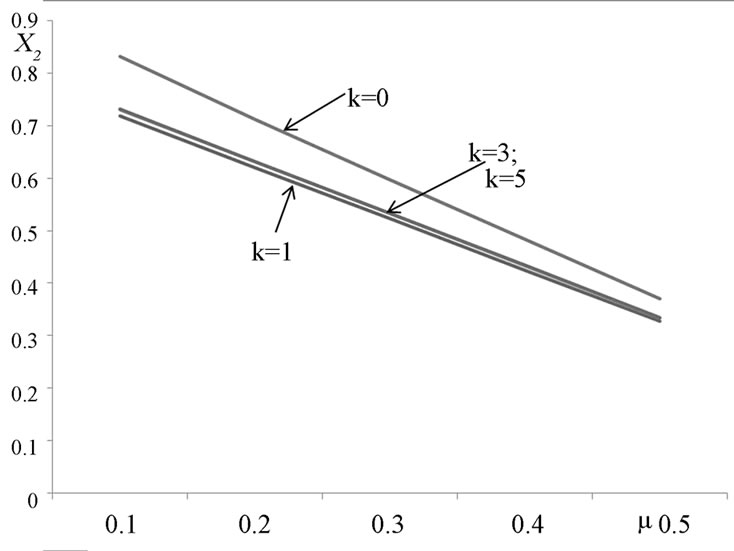
Figure 2. Variation of location of L2 with density parameter k and mass parameter μ.
At the collinear point , so that
, so that 
 and
and  Therefore,
Therefore,

For values of ,
, 
 0, A
0, A 1 the discriminant of the characteristic Equation (14) is positive when k > 0 and negative for k < 0.
1 the discriminant of the characteristic Equation (14) is positive when k > 0 and negative for k < 0.
Consequently, for k > 0, one root  of the characteristic equation will be positive and the other negative, indicating unbounded motion. This makes the collinear
of the characteristic equation will be positive and the other negative, indicating unbounded motion. This makes the collinear

Figure 3. Variation of location of L3 with density parameter and mass parameter μ.
points  unstable. For k < 0, both roots of the characteristic equation will complex (imaginary) and indicates oscillatory motion. Hence, the collinear points
unstable. For k < 0, both roots of the characteristic equation will complex (imaginary) and indicates oscillatory motion. Hence, the collinear points  are stable.
are stable.
6. Discussion
It is evident from Equations (9), (10) and (11) that the three physical parameters (density, radiation and oblateness) affect the location of collinear points. Using numerical values we obtained nine collinear equilibrium points for our problem (one from Equation (9), three from Equation (10) and five from Equation (11). By keeping the radiation and oblateness factors constant, we observed the variation in the location of the collinear points for various values the density parameter with the mass parameter.
In Figures 1-3, curve k = 0 corresponds to the density of the incompressible fluid in the spherical shell and that of the infinitesimal mass moving in the shell being the same. Curves k = 1, k = 3 and k = 5 correspond to the infinitesimal mass denser than the incompressible fluid in the shell. It is also observed that due to variation of the parameter, keeping radiation and oblateness fixed, the positions of the collinear equilibrium points shifted towards the primaries. Hence, it could be inferred that the three physical parameters have the tendency of moving the collinear points closer to the primaries.
Collinear equilibrium points are generally unstable in classical and some generalized restricted three-body problem. However, it is seen from the discriminant of the characteristic Equation (14) that when the infinitesimal mass is denser than the incompressible fluid in the shell the collinear equilibrium points are unstable and stable when the incompressible fluid is denser than the infinitesimal mass.
7. Conclusions
In studying the stability of collinear equilibrium points in Robe’s restricted three-body problem under the influence of radiation and oblateness of the primaries when the densities of the infinitesimal mass and the incompressible fluid are different nine collinear points were obtained.
The collinear points are found to be stable when the incompressible fluid in the spherical rigid shell is denser than the infinitesimal mass moving in the shell and unstable when the infinitesimal mass is denser than the incompressible fluid.
8. References
[1] A. AbdulRaheem and Singh, “Combined Effects of Perturbations, Radiation and Oblateness on the Stability of Equilibrium points in the Restricted Three-Body Problem,” Astronomical Journal, Vol. 131, No. 3, 2006, pp. 1880-1885.
[2] R. K. Sharma, Z. A. Taqvi and K. B. Bhatnagar, Celest. Mech. and Dyn. Astr., Vol. 79, 2001, pp. 119-133.
[3] J. Singh, Indian J. of Pure and Appl. Math., Vol. 34, No. 2, 2003, pp. 335-345.
[4] S. K. Shaoo and B. Ishwar, Bull. of Astr. Society. of India, Vol. 28, 2000, pp. 579-586.
[5] B. Ishwar and A. Elipe, Astrophysics and Space Science, Vol. 277, 2001, pp. 437-446.
[6] A. L. Kunisyn, Jour. of Appl. Math. and Mech., Vol. 64, No. 5, 2000, pp. 757-763.
[7] A. L. Kunisyn, Jour. of Appl. Math. and Mech., Vol. 65, No. 4, 2001, pp. 703-706.
[8] D. V. Schuerman, Astronomical Journal, Vol. 238, 1980, pp. 337-342.
[9] V. V. Szebehely, Astronomical Journal, Vol. 72, No. 1, 1967, pp. 7-9.
[10] H. A. G. Robe, Celestial Mechanics, Vol. 16, 1977, pp. 345-351.
[11] A. K. Shrivastava and D. Garain, Celest.and Mech. Dyn. Astr., Vol. 51, 1991, pp. 67-73.
[12] C. M. Giordano, A. R. Plastino and A. Plastino, Celest. Mech. and Dyn. Astr., Vol. 66, 1997, pp. 229-242.
[13] P. P. Hallan and N. Rana, Celest . Mech.and Dyn. Astr., Vol. 66, 2001, pp. 145-155.
[14] P. P. Hallan and N. Rana, Indian J. of Pure and Appl. Math., Vol. 35, No. 3, 2004, pp. 401-413.

